-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Food Science and Nutrition Engineering
p-ISSN: 2166-5168 e-ISSN: 2166-5192
2012; 2(5): 85-88
doi: 10.5923/j.food.20120205.03
Programming Technique for Animal Diet Formulation: A Non-linear Approach
Pratiksha Saxena 1, Vinay Pathak 2, Vinod Kumar 2
1Assistant Professor, School of Applied Sciences, Gautam Buddha University, Greater Noida 201308, India
2School of ICT, Gautam Buddha University, Greater Noida 201308, India
Correspondence to: Pratiksha Saxena , Assistant Professor, School of Applied Sciences, Gautam Buddha University, Greater Noida 201308, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper proposes a technique for animal diet formulation using Non-linear programming and C language. Objective of this technique is to maximize animal weight gain. Most of the existing techniques use linear approximation of objective function. This technique uses Non-linear programming, which overcomes this drawback. C language program explores the area of programming in the field of animal diet formulation. Outcome of this technique is applied on sample data and provides optimized set of nutrient ingredients to animal which fulfill the nutrient requirement better than the linear programming technique.
Keywords: Animal diet formulation, Non-linear programming, C programming
Cite this paper: Pratiksha Saxena , Vinay Pathak , Vinod Kumar , "Programming Technique for Animal Diet Formulation: A Non-linear Approach", International Journal of Food Science and Nutrition Engineering, Vol. 2 No. 5, 2012, pp. 85-88. doi: 10.5923/j.food.20120205.03.
Article Outline
1. Introduction
- Animal diet formulation techniques are in use for more than hundred years. Main objective of animal diet formulation is to provide necessary energy at different stages of animal as growth, reproduction, metabolism and lactation. Basic knowledge of animal nutrition, nutrition level of feed ingredients, feed composition and diet formulation techniques are used to formulate the animal diet. As feedstuffs vary in composition, feed analysis is an important step of diet formulation. A balanced diet should provide all necessary nutrition to animal and should simulate feeding behaviours. A nutritionaly balanced diet should be economic, easily digestible, concise, effecient and practical. Absorption and efficiency of the diet also depends on physiological function, productive function and nutritional status of animal. Different techniques have been derived in this regard using linear programming, stochastic programming, goal programming and dynamic programming. Diet should be highly digestible and should have very less adverse environmental effect.In 1960, short cut methods of solving linear programming technique were analysed[1]. A model is proposed by applying economic analysis to animal growth data[2]. A model is solved by linear programming in which elements of the tableau are stochastic[3]. A quadratic programming model is proposed and is compared to linear programming model[4]. Basics of ration formulation were firstly described by computerized linear programming[5]. It describes basic assumptions of linear programming, its application for animal diet formulation, modelling ratios, upper and lower bounds on individual feedstuffs, combinational feedstuffs and their programming by computer programs. Chance-constrained programming is used to formulate commercial feeds for animals[6]. Application of Genetic Algorithm is proposed to obtain minimum cost diet for farmed animal[7]. A linear fuzzy model is developed in which composition based inference function works for single input and single output systems[8]. Cattle diet is formulated in an Argentinean farm by applying fuzzy linear programming[9]. Excel Solver Nonlinear Programming is used to optimize performance response for broiler feed formulation[10]. Iterative linear programming is used to formulate two nonlinear optimization problems as an iterative sequence of linear programming problems[11]. Every nutrient has specific role for production, metabolism, energy, lactation and growth. Diet formulation is based on the need of specific amounts of various classes of nutrients. Nutrient classes are defined by their function in metabolism. Protein is major component of diet and is measured as Crude Protein percentage (CP). Energy is expressed as percentage of Total Digestible Nutrients (TDN). Dry Matter (DM) represents composition of chemical constituents and biological attributes of feeds. These three nutrient ingredients are necessary to formulate an effective diet. Complexity of different nutrient ingredients would possibly be better described by nonlinear relationship between them. Introduction of nonlinear programming to optimize yield and minimize feed cost in animal feed formulation may lead to better approximation as compared to linear cases. Objective of this technique is, to maximize animal weight gain by optimum use of nutrient ingredients. In this paper, it is envisaged to develop a programming technique using non-linear programming to take simultaneous effects of all nutrient ingredients. ‘C’ programming is used as a tool for formulation of programming problem. After developing the technique, result is demonstrated by using sample data.
2. Developing Environment and Technique
2.1. Data Network Operating System
- This unit of code can be installed on any earliest version of Windows operating system edition. It can be used on a single machine or on the network as per the requirement. It can also be used as ODBC and OLEDB network. This technique can be integrated with HTML, VBScript or JSP format. In order to reduce the complexity, no GUI languages are used. For quick access, it can be set as hierarchy in cloud environment.
2.2. The Programming Language
- C language is used as programming language because of fast compilation, more secure LINUX environment and less computational time. Nonlinear programming is used to formulate and optimize the diet as mathematical programming method.
2.3 Formulation Technique
- As the first step, a linear relationship is established between animal weight gain and nutrient ingredients .This relationship is established to determine the weightage and impact of these nutrient ingredients on animal weight gain. This relation is obtained by program 1.Program 1main(){Declare the variable ()}Intialized all variable equal to 0 //double a1, a2, a3, b1, b2, b3, c1, c2, c3, d1, d2, d3,det, deta, detb, detc;//double x1[max],x2[max],x3[max],y[max];Initialize the loop body for x1{statements}Initialize the loop body for x2 {Statements}Initialize the loop body for x3{Statements}Initialize the loop for y {Body of code}start of loop body(all possible combination){ Statements}a1= expression1b1= Expression2c1=Expression3d1=Expression4a2=Expression5b2=Expression 6sc2= Expression 7d2=Expression 8a3=Expression 9b3= Expression 10c3= Expression11d3=Expression 12printf("\n a1: %lf b1: %lf ,c1: %lf d1:%lfa2; %lf b2:%lf c2:%lf d2: %lf a3: %lf,b3: %lf,c3:%lf d3:%lf",a1,b1,c1,d1,a2,b2,c2,d2,a3,b3,c3,d3);det=finddet(a1,a2,a3,b1,b2,b3,c1,c2,c3); deta=finddet(d1,d2,d3,b1,b2,b3,c1,c2,c3);detb=finddet(a1,a2,a3,d1,d2,d3,c1,c2,c3);detc=finddet(a1,a2,a3,b1,b2,b3,d1,d2,d3);printf("\n det:%lf ",det);a=deta/det;b=detb/det;c=detc/det;d=sig_y-a*sig_x1-b*sig_x2-c*sig_x3;Perform comparision for solution //if(d1==0 && d2==0 && d3==0 && det==0)//printf("\n Infinite Solutions\n ");//else if(d1==0 && d2==0 && d3==0 && det!=0) //printf("\n x=0\n y=0, \n z=0\n ");//else if(det!=0)//printf("\n a=%lf\n b=%lf\n c=%lf d=%lf \n", a,b,c,d);//else if(det==0 && deta==0 && detb==0 && detc==0)//printf("\n Infinite Solutions\n ");//else//printf("No Solution\n ");}double finddet(Refernce the all variable with size declared as above){return }As second step, relationships between individual nutrient ingredients and animal weight gain are established. These relationships are established by Program 2. These relationships may be nonlinear in nature. Program 2void main(){//clrscr();int i=0,n;float x[5],y[5],xy[5],x2[5],a,b;float sx= 0.0,sy=0.0,sxy=0.0,sx2=0.0;printf("How many terms : ");scanf("%d",&n);printf("Enter the values of x\n" );for(i=0;i
2.4. Solution of the Diet Model
- Diet model can be solved any of the existing nonlinear programming method. In the sample data formulation, Kuhn-Tucker conditions are used to solve diet formulation model.
3. Discussion: Example for Demonstration
- Computation is carried over secondary data of research project experiment at National Dairy Research Institute, Karnal[14]. Briefly, the study consists of lactating sahiwal cows of second to fifth lactation number, selected from the National Dairy Research Institute herd, and divided into four groups which were switched over four times (as the number of treatments) in a Latin-square change over design. The 4 groups A, B, C and D were fed with isonitrogeneous and isocaloric concentrate mixtures, containing ground nut cake, cotton cake, cotton seedcake (undecorticated) and cotton seed cake (decorticated), respectively. In addition to the maintenance requirements, 50 gm DCP requirement, 50 percent was met through the concentrate mixture. A green fodder was given ad libitum to provide rest of the DCP and also to meet the dry matter and energy requirements. Table 1 gives composition of concentrate mixtures in respect of DCP and TDN.
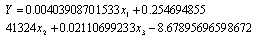 | (1) |
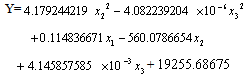 | (2) |
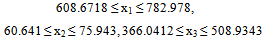 | (3) |
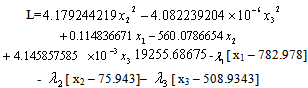 | (4) |
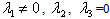 satisfying all the conditions.
satisfying all the conditions.4. Conclusions
- This technique presents a method to develop nonlinear formulation of animal diet for the objective of maximum weight gain. The technique presented in this paper formulates and solves a nonlinear program with optimum use of nutrient ingredients. It explores the use of mathematical and computerized programming in the field of animal nutrition and can be investigated in future for more variables.
References
| [1] | Wilfred Candler, 1960, A "Short-Cut” Method for the Complete Solution of Game Theory and Feed-Mix problems, Econometrica, 28(3), 618-634. |
| [2] | Brown, William G., G. H. Arscott, 1960, Animal production functions and optimum ratio, J Farm Economics, 42(1), 69-78. |
| [3] | Sabir A. Rahman, F. E. Bender, 1971, Linear Programming Approximation of Least-Cost Feed Mixes with Probability Restrictions, Am J Agricultural Economics, 53(4), 612-618. |
| [4] | Bill R. Miller, Ronaldo A. Arraes, Gene M. Pesti, 1986, Formulation of Broiler Rations by Quadratic Programming, Southern J Agricultural Economics, 141-151. |
| [5] | Black J R, Hlubik J, 1980, Basics of computerized linear programs for ration formulation, J Dairy Science, 63(8), 856-864. |
| [6] | Agway, Robert H. Stock, Terri L. Cravener, Thomas H. D'Alfonso, 1994, Using Chance-Constrained Programming for Animal Feed Formulation, Interfaces, 24(2), 53-58. |
| [7] | Rosshairy Abd Rahman, Chooi-Leng Ang, Razamin Ramli, 2010, Investigating Feed Mix Problem Approaches:An Overview and Potential Solution. Proc. World Academy of Science, Engineering and Technology, 70, 467-475. |
| [8] | D. Darvishi SalooKolayi, A. Teimouri Yansari, S. h. Nasseri, 2010, Application of Fuzzy Optimization in Diet Formulation, J Mathematics and Computer Science, 2(3), 459-468. |
| [9] | José M. Cadenas, David Pelta, Hector Pelta and Jose Luis Verdegay, 2004, Application of Fuzzy Optimization to Diet Problems in Argentinean Farms, European Journal of Operational Research, 158 (1), 218-228. |
| [10] | Guevara VR, 2004, Use of nonlinear programming to optimize performance response to energy density in broiler feed formulation, Poultry Science, 83(2), 147-51. |
| [11] | Alan G. Munford, 1996, The use of iterative linear programming in practical applications of animal diet formulation, Mathematics and Computers in Simulation, 42(2), 255-261. |
| [12] | Report of Commission on Natural Resources, 1981, National Research Council, National Academy Press, Washington, D. C. |
| [13] | Morrison, Frank B., 1957, Feeds and feeding, Twenty-second edition, The Morrison publishing company, New York, 168-201. |
| [14] | Maynard, Leonard A. and Loosli, John K., 1956, Animal nutrition, Tata McGraw Hill, 138-145. |
| [15] | Virendra Kumar, “Effect of feeding cotton seed cake with and without molasses-bound NPN compounds on nitrogen utilization and milk production in ruminants”, Ph.D. thesis, Panjab University, India, 1976. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML