1. Introduction

The framework of this study relies primarily on the work of Bandura [1], who conceptualised that efficacy beliefs have an impact on almost everything individuals do in their lives, how they think, motivate themselves, feel and behave. He coined the phrase collective-efficacy to describe an individual's beliefs about the abilities of his/her group to perform a particular behaviour, and defined collective-efficacy (CE) as a group's shared belief in its conjoint capabilities to organise and execute the courses of action required to produce given levels of attainments. CE, just like self-efficacy, is believed to be shaped by four major sources: mastery experiences, vicarious experiences, verbal persuasion and affective states [1, 2]. Unlike individual efficacy, collective-efficacy involves interactive, coordinative and synergetic social dynamics [3]. According to Bandura [1], the CE beliefs of groups can affect their goal setting; motivation; effort; persistence with challenging tasks or situations; the type of future they seek to achieve; how they manage their resources; the plans and strategies they construct; and their vulnerability to discouragement. Thus, CE is associated with traditional motivational mechanisms such as direction, effort levels, persistence, shared thoughts, stress levels, goal attainment and achievement of groups. A vast amount of research has shown that groups with high levels of CE outperform groups with low levels of CE [4]. High efficacy groups and low efficacy groups differ in several ways.

1.1. High and Low Collective-Efficacy

The existing literature on CE converges on the conclusion that groups who are confident in their ability to succeed are more effective than those who doubt themselves [1, 3]. For example, a recent meta-analysis showed that CE has a strong positive relationship with group performance, for example, in studies on reading and mathematics [4], replicating the results of an earlier meta-analysis [5]. Groups characterised by high CE are likely to have high performance expectations, work hard, set more challenging goals, persist in the face of obstacles, and are ultimately more likely to succeed than groups who do not share this belief [6]. High efficacious groups are generally positive environments that are characterised by engagement, camaraderie and cohesion [7, 8, 9]. Conversely, low efficacious groups are more likely to experience apathy, uncertainty and a lack of direction [1, 8]. Research has shown that the dysfunctional characteristics associated with low efficacy include heightened anxiety [1] and less vigilance in decision-making processes [10].

1.2. Effect of Collective-Efficacy on the Group and on the Individual

Most research on CE (also labelled 'group efficacy' or 'team efficacy') examines relationships between group perceptions and aggregate group processes. For example, CE has been shown to relate to group cohesion [9, 11], cooperation and communication [12]. Only a few multilevel studies have linked CE with individual outcomes, such as perceptions of self-efficacy (e.g., 13), and group work behaviour (e.g., 14). Researchers found that members of a group who believe in the group's collective capabilities are more likely to be motivated to work individually on tasks that contribute to group success. In contrast, self-efficacious individuals are unlikely to exert as much effort on behalf of their group if they believe that their group is incapable of handling challenging tasks [15, 16]. These observations are consistent with the theoretical arguments of Lindsley, Brass and Thomas [17], who noted that such cross-level effects are possible because efficacious groups create a context in which constructive individual behaviours are expected. Therefore, the aim of this study was to enhance both dimensions of group work: the interpersonal group work behaviour and progress, and the individual's behaviour and progress. CE has only recently begun to receive attention regarding its role in an educational setting, and the question of how perceptions of group capability might be strengthened is an understudied area in CE belief research [2, 18]. Therefore, we aimed to advance the awareness and diagnosis of CE perceptions, and to suggest ways to enhance them. The research questions were as follows:

1. What was the nature of CE in the mathematics class pre-intervention?

2. What constituted the CE of the mathematics class post-intervention?

3. How did the group work to achieve its goals? What were the learning community conditions that helped enhance the development of CE?

2. Methodology

2.1. Participants

A mathematics class of 17 female student-teachers in a college of education was chosen. The students' capabilities in various areas in mathematics were average, with two students slightly higher than average.

2.2. Design

The need for a detailed exploration of CE, the need to focus on individuals in their natural authentic setting and the need to tell the story from the participants' perspectives all provided the rational for our decision to undertake a qualitative action study. The flexibility and openness of the qualitative approach enabled revelation of tacit knowledge and better understanding [19]. Communicating and remaining in the field of the study for a prolonged period allowed us, first, to create a picture of the participants' reality in our mind, and second, to reflect deeply on our professional work as producers and enhancers of knowledge. All student-teachers gave written informed consent to their participation. They understood that the study was designed to enhance their functioning in mathematics. We made every effort to maintain their anonymity using code numbers. The participants were allowed to read the results of the analysis, if they so wished.

2.3. Research Tools and Procedure

Three research tools were used in this study: Open interviews, open non-participant observations and field notes taken pre- and post-intervention.

Nine pre- and nine post-intervention interviews were conducted with key informants. The interviews were audio-recorded and transcribed. During the interviews, the participants were given an open-ended request asked to tell us about anything related to their perception of the group's capability to execute the courses of action required to perform well in mathematics, in the classroom and at home; to tell about the group's past experiences in learning mathematics; about how much support they received from their peers; about cooperation in the group, and about what made mathematics difficult for them. Informative and elaborative questions were used and the atmosphere was relaxed. Communication was pleasant and the students' reactions to the interviewers were supportive.

Five pre- and five post-intervention observations were conducted, each lasting 35 minutes. The researchers took 10 pre- and 10 post-intervention field notes regarding the student-teachers' CE. The study procedure included data collection, analysis, intervention, renewed collection of data, reanalysis and conclusion drawing.

2.4. Intervention

We used a multiple solution task, which required bridging areas in mathematics, integrative thinking processes, high-order thinking, finding out connections and relationships, elaborations, generalizations and production of mathematical knowledge [20] in a collective form of learning.

This task suited this type of learning in that every solution to the problem found by anyone in the group could be added to the group's progress. This task was a challenge for them as a group and as individuals. We created a professional learning community that fitted the constructivists approach to the Instruction-Learning-Culture, which believes that instruction promotes the development of active learners who make use of knowledge, investigate, and evaluate their own achievements. We fostered teacher-student cooperation in learning where the teacher was considered a coach rather than the sole source of knowledge.

2.4.1. Presentation of the Task

The students were required to solve a task using as many different methods as possible, and using tools from different areas of mathematics. On obtaining the results, a discussion was held to consider the different mathematical aspects of each solution method offered by the students. Subsequently, they were asked to find additional solution methods. Given clues, they were asked what could be added to the task to increase its level of difficulty. Students had to turn the problem into a more complicated and advanced activity. They were also asked whether the same solution methods could be used in the new extended task as the methods found during the initial stage.

The intervention was implemented during two lessons lasting two hours each. The goals of the activity were stated as a challenge for the whole group, which had to work cooperatively for the group's success. The responsibility to find solutions was the group's responsibility. The members of the group asked one another questions, thought aloud, offered solutions, compared and discussed various solutions, and encouraged, helped and evaluated one another. Each suggestion was checked by all group members. The teacher did not put himself in a judgmental position of authority. The group could feel the teacher's enthusiasm, which became infectious.

2.4.2. The Task

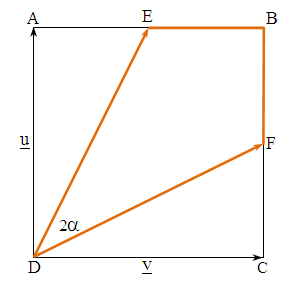
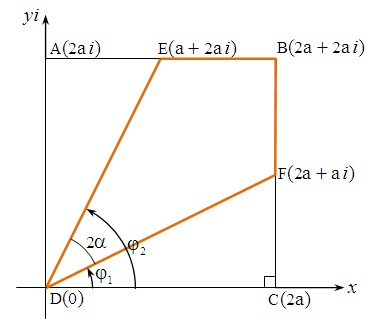
Given a square ABCD, the length of its side is 2a, as shown in Figure 1. Straight lines were drawn from vertex D to points E and F, which are the midpoints of the sides AB and BC, respectively. Calculate EDF.

Denoting: .

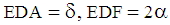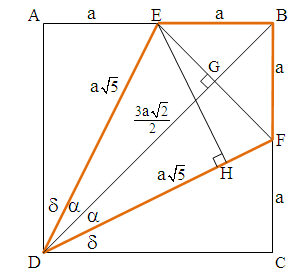Figure 1. The task

2.4.3. Stages of Preparation before Obtaining Solutions

a) By connecting points E and F, one obtains quadrilateral DEBF, which is a kite, and therefore: .

b) Calculate the following segment lengths using the Pythagorean theorem: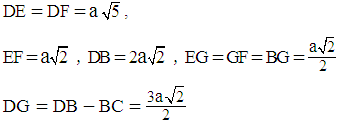

c) Calculate the area of triangle :

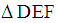(1) By subtracting the areas of the right angled triangles from the area of the original square.

(2) From the product .

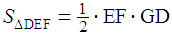(3) By using Heron’s formula – which requires command of algebraic manipulations due to the presence of expressions with radicals.

In all three methods we obtain: .

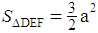2.4.4. Calculation of the Angle

Method A – Trigonometry of right-angled triangles

Method B – Using the Law of Cosines in the triangle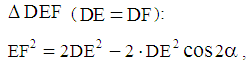

Substituting the values of EF and DE, we obtain:

Method C – Using the Law of Sines in triangle :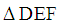

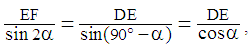Substituting the values of EF and DE and using the formula for the sine of a double angle, we obtain 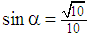, and using the formula , we obtain:

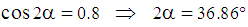Method D – Using the area of a triangle:

From the trigonometric formula for the area of a triangle, we obtain:

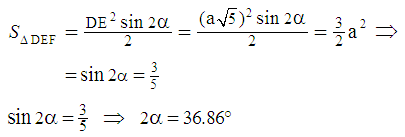Method E – From analytic geometry:

We place the vertices of the square in a system of coordinates, where vertex D lies at the origin, and the coordinates of the other vertices are: 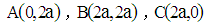, and also: 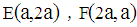, as shown in Figure 2. Using this notation, the slope of straight line DF is 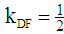, the slope of straight line DE is 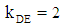, and from the formula for the tangent of the angle between two straight lines, using their slopes, we obtain: .

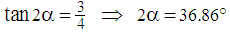Figure 2. Method E

Method F – Using vectors.

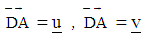We denote: , with 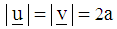, as shown in Figure 3.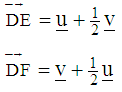

By comparing the two expressions we obtain: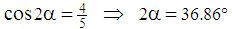

Figure 3. Method F

Method G – Using complex numbers.

We place the square in a Gauss plane, as shown in Figure 4.

The coordinates of the points A, B, C, D, E and F are shown in the figure.

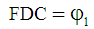
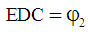
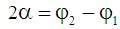Using this notation, the representation of the complex number DE is:

and that of the complex number DF is: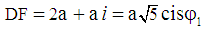

Therefore, using the trigonometric representation, we have:

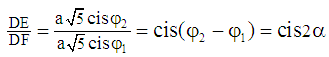In the algebraic representation we have:

,

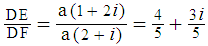Hence, 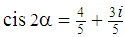, and therefore:

.

Figure 4. Method G

Method H – Finding the angle from a known triangle.

Let EH be the altitude dropped from the vertex E to the side DF of the triangle .

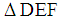From the area of the triangle and the length 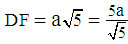, we find that 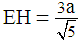, and from the Pythagorean theorem we find that .

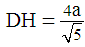Hence it follows that the lengths of the sides of the right-angled triangle 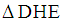satisfy the ratio 3:4:5. We know that in that triangle the angles are approximately 37°, 53°, 90°.

2.4.5. Some Suggestions by the Students for Increasing the Level of Difficulty

a) Making the calculation of the angle with the points E and F not being the midpoints of the sides, as shown in Figure 5 (the formed quadrilateral is not a kite).

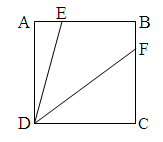Figure 5. Suggestion A

b) Making the calculation of the angle with the points E and F placed at different locations on the continuations of the sides outside the square, as shown in Figure 6.

Figure 6. Suggestion B

c. Making the calculation of the angle with the points E and F being the midpoints of the sides of a rectangle, as shown in Figure 7.

Figure 7. Suggestion C

d. Making the calculation of the angle with the points E and F being the midpoints of the sides of a rhombus with a given angle, such as 45°, 60°, as shown in Figure 8 (A kite is formed).

Figure 8. Suggestion D

2.4.6. Analysis of the Methods for Solving the Original Task and the Proposed Extensions of the Task

As part of their joint work, the students found the solutions from 1-4, where most of them found the solutions from 1-2, which were based on finding segment lengths using the Pythagorean theorem, followed by the use of trigonometry of right-angled triangles. Naturally, these solutions were the simplest and suitable for students who had not yet possessed full command of the advanced tools (the Law of Cosines, the Law of Sines, analytic geometry, complex numbers and vectors). Some students did use the advanced tools, based on their experience in dealing with more complex tasks in which there were no right angled or isosceles triangles, but did not obtain the desired result during the time allotted by the teacher to that end. The second part of the first meeting was dedicated to a discussion of the methodical aspects of the task regarding the following points: during which stage of the aforementioned solutions the students might make mistakes or encounter difficulties; was each stage given precise mathematical justifications as required; why do some students immediately start with the 'improved tools', even though simpler methods exist. After providing some hints, the students were asked to find solutions using 'improved tools' e.g. a joint computer. In this part, methods e to g were found. A methodical discussion was held, and its main conclusion was that the ability of using 'improved tools' had tremendous importance, since only these tools could allow the students deal with more difficult tasks, and that the 'simple tools' are particular cases of the 'improved tools'.

In terms of changes in the task aimed at increasing its difficulty, it is important to note that the proposals that appear in the paper are only part of the proposals offered by the students. One student suggested constructing a computerized applet (using the GeoGebra software) to investigate the task dynamically, as the data of the problem change (as proposed by the students), in order to observe their effect on the result immediately on the screen.

In a feedback page, the students mentioned their satisfaction with dealing with the problem, and that the use of the 'improved tools' was an opportunity for practice for them. In general, the students noted that solving a task using different methods revealed the interrelation between the different branches of mathematics, and brought out the beauty of mathematics.

2.5 Data Analysis

A CE diagnosis was reached by using constant comparative analysis and grounded theory techniques [19, 21]. The unit of analysis was a statement/an idea. The units were gathered under categories/constructs by initial, axial and selective coding. Analysis began during data collection and continued after its conclusion. The constant comparison of units was adapted, changed and redesigned as the study proceeded, and resulted in a refined list of categories that were developed into conceptual abstractions called constructs. Core constructs containing dense descriptions of evidence were formed. The concept map was sampled only when repetition of the same constructs was obtained from multiple cases and when new units did not point to any new aspect [21]. The qualitative methodological frame used for analysis was the criteria-oriented methodology, which assumes that open analyses are often influenced by researchers' own perspectives [22]. Charmaz [21] argued that preconceived theoretical concepts may provide starting points for looking at the data, but they do not offer automatic codes for analyzing these data. Of all qualitative frames, criteria-oriented methodology is closest to quantitative methodology. We spent a long time in the study setting, thus enabling interpretation of the meaning that individuals attributed to their beliefs. This methodology produced a CE beliefs diagnosis pre- and post-intervention. Data source triangulation [19] was used to ensure the trustworthiness of the findings presented in the study. We made an effort to verify what students were describing in their interviews using the other data sources. Member checks were employed to ensure the integrity of the study. Triangulation was achieved when the content articulated by the student-teachers during interviews became evident in their actions and when information was repeated several times in different interview settings. The researcher's results were compared with those of an external rater (n = 10), and agreement was achieved.

3. Results

Data collection included 2321 units of evidence pre-intervention and 2102 units post-intervention. Emerging results were as follows:

3.1. CE Beliefs Diagnosis Pre-Intervention

We wished to obtain a picture of the students' CE beliefs in mathematics pre-intervention. Seven constructs emerged from this analysis, as illustrated in Figure 9:

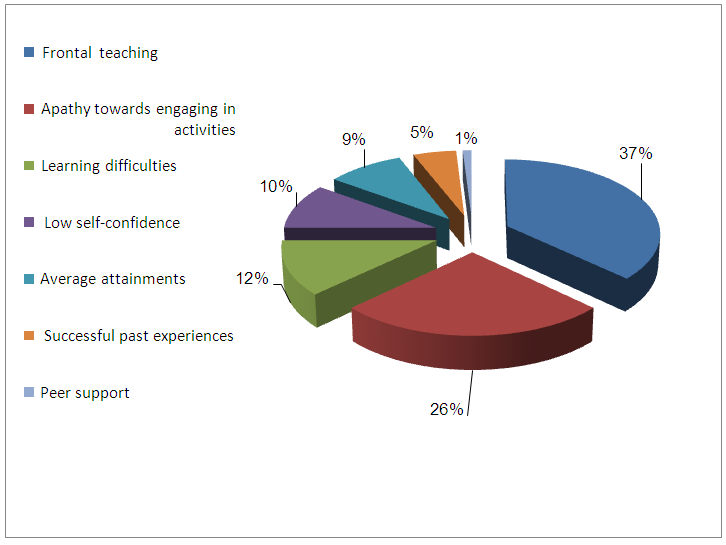Figure 9. The students' pre-intervention CE belief profile to learn

The first construct, containing 37% of the evidence, shows descriptions of a frontal teaching style, e.g., the teacher explains theorems and the students write in their notebooks,

"When one student answers a question, the rest sit passively". (Observation).

The second construct (26%) describes students' apathy to mathematics activities:

"I never raise my hand in maths lessons unless I'm asked to do so". (Interview)

The next two constructs contain evidence of difficulties (12%) and low self-confidence (10%). Student attainments were reported as average (9%):

"We don't know math'; 'We can't do it"; "We usually get Cs and Ds, also Bs…but that is rare". (Interviews)

Students experienced average levels of motivation, thereby creating an atmosphere that neither encouraged nor discouraged performance behaviours. The students emerged as indifferent and often expressed resistance to engage in performance:

"D. shrugs shoulders at the teacher's request to prove the theorem, after a few requests, the teacher turns to another student, who says he doesn't know". (Observation)

Looking at the class as a group showed uncertainty, lack of direction, low cooperation and communication, and sometimes heightened anxiety when students were asked to present their work. Peer support was low; each student learnt individually, although they sometimes worked in pairs (1%). Successful past experiences, although very low (5%), gave us the hope that change is possible. This constituted the answer to question 1.

3.2. CE Beliefs Diagnosis Post-Intervention

To answer the question of how the students' CE beliefs about mathematics learning looked post-intervention, we analysed the data gathered following the intervention. Emerging constructs are illustrated in Figure 10:

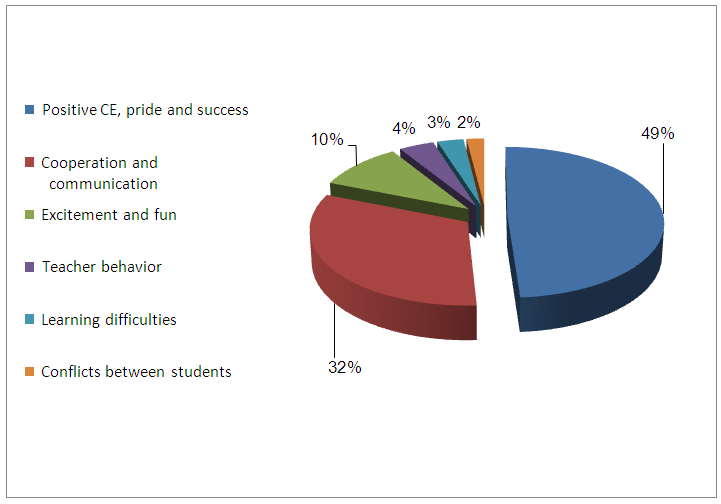Figure 10. The students' post-intervention CE belief profile to learn mathematics

The first emerging construct describes positive CE beliefs towards mathematics, satisfaction, high morale, pride in belonging to this group and success at producing multiple solutions to one problem (49%). CE was enhanced and students' attainments were improved:

"If we found eight solutions, we can try more. Please give us more problems like this one". (Observation)

"I feel free to act in class". (Interview)

"I've never been so good before! We are not stupid". (Observation)

The second construct describes interactive work, cooperation and communication (32%):

"We discussed every method and evaluated the pros and cons and helped each other; we wanted to succeed". (Interview)

The third (10%) describes excitement and fun:

"One student moves to the corner of the class where he works with another student. Two show their solution to the class and get feedback. They are busy again.

They seem happy and excited". (Observation)

"I had fun, I made my suggestion, they said it was great". (Interview)

"I connected what we studied in the past to this and it came up". (Interview)

"This task is interesting and stimulating". (Interview)

The fourth (4%) construct contains evidence of the teacher working as one of the students:

"I can't see the teacher; he is probably busy in that corner with the students". (Observation)

Learning difficulties did not disappear (3%) but they were not mentioned. Instead, success was emphasized and conflicts between students were rare (2%). Inter-rater agreement on data analysis was 86%. This description was the answer to questions two and three.

4. Discussion

This qualitative study explored a multiple solution task learned cooperatively in a self-directed professional learning community, which was shown to enhance student-teachers' mathematics CE beliefs and attainments as individuals and as a group. In this section, we will discuss the use of the qualitative methodology and tools for diagnosing CE beliefs for mathematics; how this task and its organisation enabled enhancement of group and individual CE beliefs and success, and the contribution of this action research to our professional work.

4.1. The Use of Qualitative Methodology for Diagnosing CE Beliefs for Mathematics

This study suggests a broadening of the methodology for diagnosing efficacy beliefs for mathematics, suggesting a qualitative method of assessing CE. Efficacy beliefs have been assessed by quantitative questionnaires, in which students are asked to rate their confidence about their group's capability to perform a specific task on a certain level, which ends in a score on a scale. We believe that a final score is insufficient for a deep understanding and therefore offered a profound analysis to elicit and diagnose beliefs in a more detailed, authentic and precise manner than via questionnaires. This macro-analytic assessment observes the individual's mechanism of mathematics efficacy beliefs as a whole, which is not only close to reality, but is the authentic reality itself. This methodology suits our purpose in that it uses authentic tools in an authentic setting, and offers students a fair chance to present themselves as they wish. The participants responded positively and were willing to supply information about their beliefs, personality and experiences. The constructs were generated by repeated analyses, and qualitative validity was achieved. The close researcher−participant relationship facilitated the participants' open reflection and cooperation with the researcher, and the attainment of new insights. For tracing problems and tailoring interventions, an open profile of efficacy beliefs is far more effective than an efficacy score on a scale.

4.2. The Contribution to Achievement of the Multiple Solution Task and its Organisation

Developing students’ ability to think, prove and reason is an important goal of the mathematical curriculum standards in many countries [23, 24, 25]. Both the task and its organisation contributed to achievement:

4.2.1. Using a Multiple Solution Task for a Group Activity

A multiple solution task is a significant learning process in which students can develop and strengthen mathematical thinking, understanding and knowledge, and expand their horizons. It involves renewed effort to focus on seeking solutions, not just memorising procedures. Using one method to solve a problem might leave the students indifferent, but offering different solutions to the same problem might elicit excitement and wonder [26]. We found that the multiple solution task was appropriate for a group activity, in that it gave every member of the group a chance to try his/her own capabilities in a 'protected' unthreatening environment. A first attempt that ended in failure did not scare the students, who looked for new ways, while encouraging and helping one another. Solving problems in multiple ways cooperatively allowed students to compare and evaluate the pros and cons and to develop flexibility, which reduced their sense of isolation. Pedagogically, it was not only application of knowledge, but also its assessment.

4.2.2. Developing Divergent Thinking: Connecting Different Mathematics Realms

Problem solving and proofs have always played a major role in mathematics. Furthermore, using a number of different proof techniques — from within and between several mathematics domains—to solve one specific problem can demonstrate the connections between these domains. In this study, using methods from a wide variety of different mathematical domains, students found solutions to one specific, interesting geometry problem. This task promoted divergent thinking, which facilitated the production of eight solutions. When material is approached from different points of view, it enhances students’ high order thinking and understanding, which is very important for mathematics development. Mathematicians tackle a mission from different points of view. By encouraging our students to do the same, they, too, learned to appreciate the value and the pleasure in this task. It was fascinating to realise how this contributed to the CE beliefs of the group:

"I felt free to try things in maths because I did it with my friends". (Interview)

Connecting various mathematics branches and arriving at elegant aesthetic solutions provided a great feeling of accomplishment.

4.2.3. Creativity

The notion of divergent thinking is theoretically and empirically associated with creative potential [27]. The multiple solutions offered by the students showed the creative potential in connecting various domains of mathematics. Students used previous knowledge in Euclidean geometry, trigonometry, analytic geometry, vectors, algebra, complex numbers and various theorems to produce novel, original and unexpected solutions. The multiple solutions for one task demonstrated the connection between different areas of mathematics, which, according to Stupel and Ben-Chaim [27], gives the students the sense that mathematics is an interconnected science and not a collection of isolated topics. In most school textbooks worldwide, mathematics problems are organised according to specific topics that are presented in the curriculum. Students tend to understand that certain problems are connected to specific topics and, hence, assume that only one method exists for solving each problem. They emphasised that the NCTM (National Council of Teachers of Mathematics, USA) standards [25] also recommend that teachers present tasks that exhibit the connection between different mathematical domains. Although this is not easy, there is certainly a need to encourage such activities in class [26]. Teachers would do well to apply knowledge from different mathematical domains, as much as possible, to promote better understanding and high order thinking, which contribute to creativity. Leikin [28] found that multiple-solution tasks encouraged three hallmarks of mathematical creativity: fluency, flexibility and novelty. This task invited the students to search for different solutions in various directions, and when performed as a group mission, fostered CE beliefs.

The multiple possibilities demonstrated the aesthetics, beauty, wealth and elegance of mathematics. Multiple ways of thinking is a basis for creativity as it leads to unexpected novelties and understanding of mathematics, which have the potential to enhance human society.

4.2.4. Creating a Supportive Setting for CE Beliefs Development

It was obviously not the task alone that promoted mathematical CE beliefs, but the mode of implementation. The cooperative learning served as a context in which CE information sources could emerge: CE beliefs are likely to be both individually and socially constructed. The extent to which the organisational context fosters group cohesion is likely to be the extent to which the sources of efficacy information are socially constructed, and a shared belief in the group's capacity emerges [29]:

The interpreted result of previous performance is the most powerful source of efficacy information because having performed a task provides the most authentic proof of ability to perform in the future [1]. Given that CE beliefs are socially constructed, the group mastery experiences, (e.g., any solution obtained), were positively interpreted, evaluated and nurtured as part of the organisational learning, which contributed to CE development.

CE beliefs are also influenced by vicarious experiences [1]. Vicarious experiences are the interpreted result of someone else's performance gained from observing someone model a skill or perform a task. Part of one's vicarious experience also involves social comparisons made with others. Social comparisons and peer modelling are powerful influences on developing self-perceptions of competence. Viewing a successful performance raised the observer's efficacy beliefs that the group possesses the capabilities to perform a similar activity successfully:

"M. did it! Yeah! I'm lucky to be in this class". (Observation)

As Ross et al. [29] suggested, vicarious experiences were derived from increased interactions among students. Knowledge was exchanged and students benefitted through learning from their peers and from their teacher, who acted as a member of the group. Their belief in the ability of the group as a whole increased. Opportunities for cooperative learning influenced the students' perception of vicarious experiences by exposing them to their friends' knowledge and skills.

Social persuasion, the third source of efficacy beliefs, is the interpreted result of encouragement or feedback from others about the effectiveness of the group [1]. Ross et al. [29] suggested that the interactive dynamics of a group is likely to determine whether the group members can be persuaded that they constitute an effective team. Therefore, organisational processes that support team cohesion are likely to influence the group members' perceptions of social persuasion. In this study, we found that cooperative learning influenced the students' perceptions of social persuasion. The opportunity to benefit from their peers' knowledge and skills in collaborative conversations convinced them of their group effectiveness. The following shared personal practice example might be illustrative:

"Let's connect the two ideas. I see another solution—look"! (Observation)

"I've learned a lot from D. We discussed which solution was easier, which was more elegant". (Observation)

Social cognitive theory suggests also that group dynamics plays a role in CE [1], hence, positive working relationships acted as a source of social persuasion encouraging the students to believe that their group was capable of being effective in the future. Collaboration also allowed students to assess their friends' teamwork behaviour [14]. As the students in this study experienced how well the group worked together, they had a sense of CE. Several studies have investigated collaboration as a factor that might have a promoting influence on CE. The student working with a peer, as in the present study, must evaluate the peer’s idea, then his/her own idea, select appropriate ideas and then build on them. On the one hand, the peer’s different background and knowledge base may contribute different perspectives for consideration. On the other hand, diversity may be very wide, causing difficulty in finding an agreed-upon solution [30]. A low percentage of disagreement was found. We gave our students the chance to work collaboratively to stimulate the discovery of multiple solutions because we all learn by examples, by watching techniques, strategies and approaches used by others in the creative process. The literature review indicates that cooperative interaction has considerable impact on the stimulation of higher order thinking and creativity [31]. Working collaboratively afforded the students a genuine feeling of enthusiasm and joy exhibited by many creative people as they make something new [32].

Affective states are the fourth source of efficacy beliefs that contribute to CE [1]. The atmosphere that we created in this class tolerated pressures and crises concerning the task, and caused positive affective states when students were coping with the mathematics problem. Positive emotions emerged after successes. The students gained a sense of commitment to accomplish the task. Positive interactions generated excitement about their work that generated feelings of confidence that this group could successfully help them learn. The organisational conditions that supported group interaction, collaboration and cohesion supported the social construction of CE beliefs by reducing the stress usually associated with mathematics tasks. This study extends the findings by suggesting some more specific supportive behaviours that influenced our students' CE: the dispositions of openness and caring influenced the students' perceptions of positive emotional states. Sense of community imbued students with feelings of confidence in the group's ability:

"I'll do my best in this class; together we can do a lot"! (Interview)

4.2.5. Creating a Self-Regulated Learning Community

Mathematics research shows that self-regulation has an effect on mathematical performance [33]. The students believed that opportunities to take on challenging tasks, practise their learning, develop a deep understanding of subject matter, exert effort, and take responsibility would give rise to their academic success, which is supported by literature [34]. In part, these characteristics may help to explain why self-regulated learners usually exhibit a high sense of self-efficacy [35]. These learners hold incremental beliefs (as opposed to fixed views) about intelligence and attribute their successes or failures to factors within their control, e.g., effort expended on a task, effective use of strategies [36]. Creating a self-directed learning community that takes responsibility over its learning processes fostered CE beliefs.

4.2.6. The Role of the Teacher

According to the literature, social persuasion might entail encouragement of feedback from a leader [29]. The teacher did not stop reinforcing the students when working inside the group:

"What a beautiful solution"! Turns to another student: "'Dan, isn't it great, ha?" (Observation)

The teacher's pleasure and enthusiasm fostered a positive mood that influenced CE beliefs. This result is in line with more recent studies of the impact of transformational leadership actions on CE (e.g., 37), and performance feedback that influences CE beliefs [6, 8].

The teacher used strategies, expended effort, persisted, had high performance expectations, worked hard and gave clues when students faced obstacles. The students experienced cohesion.

"M., we've got to do it, we can! Let's try trigonometry". (Observation)

They wanted to contribute to the group success and succeeded in attaining the outcomes. The teacher provided opportunities for group members to interact, which led to the emergence of CE beliefs. We found ourselves in a classroom with a high degree of mutuality, shared responsibility and confidence in the conjoint capability of the group.

"We are good because everyone wants to do it well". (Interview)

The students became enthusiastic, too. We could see that they were having fun and felt the beauty of Mathematics. Our observations and impressions created a holistic understanding of a group, whose cooperative learning created a sense of cohesion that influenced CE.

4.2.7. Enhanced Group and Individual Attainments

Researchers have found that CE beliefs contributed to team performance over and above the team's actual capability [6]. Evidence shows that the attainments of the students in the present study outperformed their attainments pre-intervention, and that the teacher and the students were surprised at the outcomes:

Teacher: "I've taught many classes of this level before, and have never seen such noticeable and remarkable progress; you did a wonderful job" ! (Observation)

Student: "I feel I'll do better in maths from now on". (Interview)

This research provides new theoretical insights for advancing performance in mathematics. CE has important performance implications for improving operational outcomes in mathematics higher education.

4.3. Reflection on our Professional Work

Social cognitive theory posits that an individual's behaviour is primarily learned through his/her observation of others as well as through interaction with his/her environment. Thus, by observing the reciprocal relationships between members of the group, we discovered that this group of student-teachers believed that they could work together to produce effects, and that they persisted and made the effort for the success of the collective learning task. The group's aspiration and motivational investment in their undertakings, their morale and resilience to stressors, and finally, their high performance accomplishments, also fostered mathematics individual's self-efficacy. We researchers had long conversations among ourselves. We sensed the progress was being made and came to the conclusion that group attainments are the product not only of the shared intentions, knowledge and skills of its members, but also of the interactive, coordinate and synergistic dynamics of their transactions. This idea supports Bandura's theory [7].

5. Conclusions and Implications for the Future

Mathematics educators agree that linking mathematical ideas by using more than one approach to solving the same problem is an essential element in the development of mathematical knowledge, reasoning, flexibility and creativity (e.g. 25, 38, 39). By encouraging students to look for multiple solutions to a problem, we gained a real feeling of working as mathematicians, who connect between the various branches of mathematics and discover original solutions. Mathematics educators are advised to introduce many authentic multiple solution tasks into their teaching program. Mathematics teachers should have rich, multidimensional pedagogical content knowledge so that they may incorporate a variety of problem-solving methods and strategies into their teaching [40]. The NCTM [25] standards call for special initiative from the teachers in this regard.

This research has demonstrated the potentially powerful nature of CE beliefs to raise students' effort, resilience and learning outcomes in mathematics. Confidence perceptions that start to emerge after team formation appear to influence subsequent individual behaviour [7, 16]. According to the literature, factors that have been argued to influence CE perceptions include process interventions aimed at increasing cooperation [8], verbal persuasion by a leader [12] and positive feedback on initial performance [14]. Early efforts that target each of these factors, according to the results of Tasa et al. [16], have positive long-term implications for the group. Therefore, we recommend organising such activities in mathematics teaching. In light of this research, it would be reasonable to advise groups to build a strong sense of CE, to be sure they set more difficult goals, overcome obstacles and ultimately achieve success.

This exploration into the antecedents of CE beliefs found the professional cooperative learning community to be a potentially powerful organisational context conducive to the development of students' CE beliefs that facilitate student learning. This study represents a step forward in furthering our understanding of how a task in an organisational context influenced the development of a group's CE beliefs and attainments. The first theoretical implication of this study, then, is that both the multiple solution task and the group's organisational context were significant antecedents of mathematics CE beliefs, and future research should expand this line of research.

The findings of this study suggested that the teacher played an important role in fostering the interactive dynamics necessary for the development of CE by acting as part of the learning community. His actions not only influenced the perception of mastery experiences, vicarious experiences, social persuasion and affective states, but focused students' attention on the group as a whole. The literature supports these findings. Wu, Tsui and Kinicki [41] found that certain leadership actions can be positive predictors of CE because they elevate the salience of the group and its capabilities. Further research might investigate specifically how the teacher's leadership actions influence students' CE.

In terms of practical implications, this intervention increased CE beliefs with the outcome expectation of increased student achievement. Our findings suggest that attention should be paid to classes as professional learning communities that develop cooperative learning.

Helping to ensure that students have the necessary thinking skills to learn mathematics effectively is one of the most important challenges. Transforming their classes into small organisations with strong CE can provide students with a means to achieve this goal.