-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Control Science and Engineering
p-ISSN: 2168-4952 e-ISSN: 2168-4960
2013; 3(1): 1-7
doi:10.5923/j.control.20130301.01
Synchronization of Mimas-Tethys System with Driven Damped Pendulum Using a Robust Adaptive Sliding Mode Controller
1Department of Mathematics, Zakir Husain College, University of Delhi, New Delhi 110002, India
2Department of General Requirements, College of Applied Sciences, Nizwa, Oman
Correspondence to: Mohammad Shahzad, Department of General Requirements, College of Applied Sciences, Nizwa, Oman.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we have synchronized the Mimas-Tethys system (MTS: Natural moons of Saturn) with driven damped pendulum (DDP) using a robust adaptive sliding mode controller (RASMC) together with uncertainties, external disturbances and fully unknown parameters. A simple suitable sliding surface, which includes synchronization errors, is constructed and appropriate update laws are used to tackle the uncertainties, external disturbances and unknown parameters. All simulations to achieve the synchronization for the proposed technique for the two non-identical systems under consideration are being done using Mathematica.
Keywords: MTS, Synchronization, RASMC
Cite this paper: Ayub Khan, Mohammad Shahzad, Synchronization of Mimas-Tethys System with Driven Damped Pendulum Using a Robust Adaptive Sliding Mode Controller, International Journal of Control Science and Engineering, Vol. 3 No. 1, 2013, pp. 1-7. doi: 10.5923/j.control.20130301.01.
Article Outline
1. Introduction
- Since more than the last two decades, the control and stabilization of chaos synchronization of chaotic systems has become more and more popular in recent years and received a considerable interest among nonlinear scientists. Chaos is a phenomenon of nonlinear dynamics that has some specific characteristics such as extraordinary sensitivity to initial conditions and system parameter variations, broad Fourier transform spectra and fractal properties of the motion in the phase space. Due to these especial characteristics, chaos has been used in many practical engineering areas such as chemical reactions, power converters, secure communications, information processing, biological systems and mechanical systems[1–3] and various control techniques have been proposed for controlling and synchronizing of chaotic systems, including sliding mode control, optimal control, adaptive control, nonlinear feedback control, backstepping method, passive control, fuzzy logic control, PID control, etc[4–11]. Most of the above mentioned works on chaos synchronization have focused on chaotic systems without model uncertainties and external disturbances. It has been observed practically that structural variations of the systems and un-modeled dynamical uncertainties are present in the chaotic system dynamics due to the modeling errors. So, synchronization of chaotic systems with uncertainties and external disturbances is effectively significant in the applications. In this direction, some researchers have proposed a number of techniques for synchronization of uncertain identical as well as non-identical chaotic systems that includes nonlinear feedback control, sliding mode control, backstepping procedure, linear state feedback control, active control and neural fuzzy control[12–21].Nevertheless, the previous techniques have studied chaotic systems with fully (or partially) known parameters. While, in practice, it is hard to exactly determine the values of the system parameters in priori. Therefore, synchronization of chaotic systems with unknown parameters is essential and useful in real-life applications. Consequently, some approaches, such as sliding mode control, finite-time based control, adaptive control, optimal control, fuzzy & backstepping control have been developed for synchronization of two identical as well as nonidentical chaotic systems with unknown parameters[22–34]. Sliding mode control[35] is a robust control method which has many interesting features such as low sensitivity to external disturbances and robustness to the plant uncertainties due to structural variations and un-modeled dynamics. The sliding mode controller is composed of an equivalent control part that describes the behavior of the system when the trajectories stay over the sliding surface and a variable structure control part that enforces the trajectories to reach the sliding surface and remain on it evermore. Adaptive control is a suitable approach to overcome system uncertainties, especially uncertainties derived from uncertain parameters. Adaptive sliding mode control has the advantages of combining the robustness of the sliding mode control with the tracking facilities of the adaptive control.The main purpose of this paper is to study the synchronization phenomenon of a MTS with DDP using a robust adaptive sliding mode controller (RASMC) in the presence of uncertainties, external disturbances and fully unknown parameters in both master and slave chaotic systems[36] together with the assumption that the bounds of the uncertainties and external disturbances are unknown in advance. A simple suitable sliding surface, which includes synchronization errors, is constructed. Appropriate update laws are derived to tackle the uncertainties, external disturbances and unknown parameters. Then, on the basis of the update laws, the RASMC is designed to guarantee the existence of the sliding motion. The stability and robustness of the proposed RASMC is proved using Lyapunov stability theory for the MTS and DDP.
2. Description of RASMC
- For the n-dimensional master and slave systems[36] with uncertainties, external disturbances and unknown parameters are given as follows:Master system:
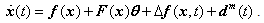 | (2.1) |
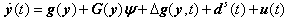 | (2.2) |
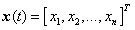 are the state vectors,
are the state vectors, 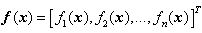 are the continuous nonlinear functions,
are the continuous nonlinear functions, 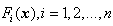 , is ith row of an matrix
, is ith row of an matrix 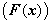 whose elements are continuous nonlinear functions,
whose elements are continuous nonlinear functions, 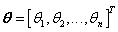 are the unknown vector parameters,
are the unknown vector parameters, 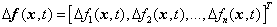 and
and 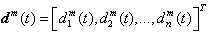 are the vectors of unknown uncertainties and external disturbances of the master system respectively.
are the vectors of unknown uncertainties and external disturbances of the master system respectively. 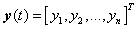 are the state vectors,
are the state vectors, 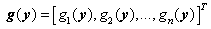 are the continuous nonlinear functions,
are the continuous nonlinear functions, 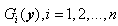 , is ith row of an
, is ith row of an 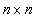 matrix
matrix 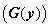 whose elements are continuous nonlinear functions,
whose elements are continuous nonlinear functions, 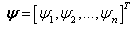 are the unknown vector parameters,
are the unknown vector parameters, 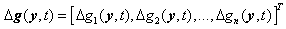 and
and 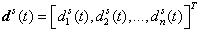 are the vectors of unknown uncertainties and external disturbances of the slave system, respectively, and
are the vectors of unknown uncertainties and external disturbances of the slave system, respectively, and 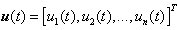 is the vector of control inputs.Assumption 1: Since the trajectories of chaotic systems are always bounded, then the unknown uncertainties
is the vector of control inputs.Assumption 1: Since the trajectories of chaotic systems are always bounded, then the unknown uncertainties 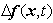 and
and 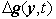 are assumed to be bounded. Therefore, there exist appropriate positive constants
are assumed to be bounded. Therefore, there exist appropriate positive constants 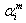 and
and 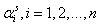 such that
such that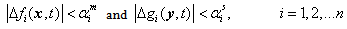 | (2.3) |
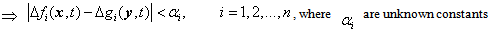 | (2.4) |
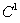 , i.e.
, i.e. 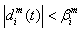 and
and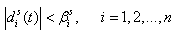 | (2.5) |
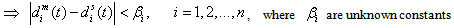 | (2.6) |
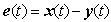 . Then from (2.1) and (2.2), the error dynamics can be written as:
. Then from (2.1) and (2.2), the error dynamics can be written as: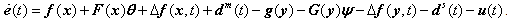 | (2.7) |
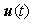 is designed such that the asymptotical stability of the resulting error system (2.7) can be achieved in the sense that
is designed such that the asymptotical stability of the resulting error system (2.7) can be achieved in the sense that 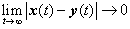 for the systems under consideration.Let us consider now, the appropriate sliding surface with the desired behavior. Therefore, the sliding surface suitable for the technique can be designed as:
for the systems under consideration.Let us consider now, the appropriate sliding surface with the desired behavior. Therefore, the sliding surface suitable for the technique can be designed as: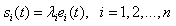 | (2.8) |
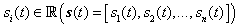 and the sliding surface parameters
and the sliding surface parameters 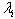 are positive constants.After designing the suitable sliding surface, let us determine the input control signal
are positive constants.After designing the suitable sliding surface, let us determine the input control signal 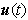 to guarantee that the error system trajectories reach to the sliding surface
to guarantee that the error system trajectories reach to the sliding surface 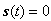 (i.e. to satisfy the reaching condition
(i.e. to satisfy the reaching condition 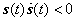 ) and stay on it, forever. Therefore, to ensure the existence of the sliding motion a discontinuous control law is proposed as:
) and stay on it, forever. Therefore, to ensure the existence of the sliding motion a discontinuous control law is proposed as: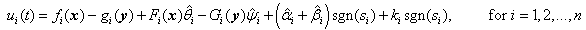 | (2.9) |
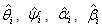 are estimations for
are estimations for 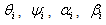 respectively and
respectively and 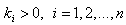 are the switching gain constant.To tackle the uncertainties, external disturbances and unknown parameters, appropriate update laws are defined as:
are the switching gain constant.To tackle the uncertainties, external disturbances and unknown parameters, appropriate update laws are defined as: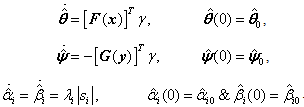 | (2.10) |
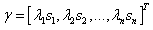 and
and 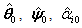 and
and 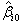 are the initial values of the update parameters
are the initial values of the update parameters 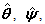
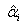 and
and 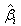 respectively.In order to minimize the chattering effect due to signum function, we are replacing the
respectively.In order to minimize the chattering effect due to signum function, we are replacing the 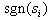 by
by 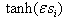 for
for 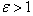 . Figure 1 shows that our results will not be affected. Therefore the new control input can be written as:
. Figure 1 shows that our results will not be affected. Therefore the new control input can be written as: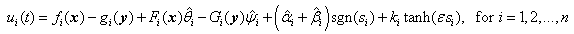 | (2.11) |
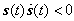 and to ensure the occurrence of the sliding motion, we have the following theorem.Theorem 1: Consider the error dynamics (2.7), this system is controlled by
and to ensure the occurrence of the sliding motion, we have the following theorem.Theorem 1: Consider the error dynamics (2.7), this system is controlled by 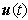 in (2.9) with update laws in (2.10). Then the error system trajectories will converge to the sliding surface
in (2.9) with update laws in (2.10). Then the error system trajectories will converge to the sliding surface 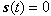 .In this regard, we consider a Lyapunov function (that is a positive definite function also) as follows:
.In this regard, we consider a Lyapunov function (that is a positive definite function also) as follows: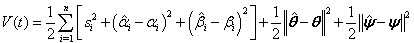 | (2.12) |
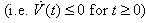 .
.3. Description of the Systems
- Elliptically orbiting planar oscillations of satellites in the solar system make an interesting study. In this paper, we synchronize the dynamical models of MTS with DDP using RASMC. The Hamiltonian (H) of the nonlinear dynamical model of the Mimas-Tethys system is written from[37] in order to study the synchronization behavior.
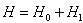
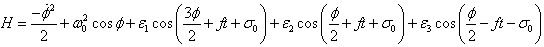 | (3.1) |
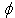 is the argument depending on the mean longitude of Mimas,
is the argument depending on the mean longitude of Mimas, 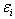 are the parameters depending on the tidal force (for
are the parameters depending on the tidal force (for 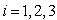 ), f is the main frequency,
), f is the main frequency, 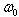 is the mass distribution parameter and
is the mass distribution parameter and 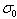 is a constant.Using Hamilton’s canonical equations
is a constant.Using Hamilton’s canonical equations 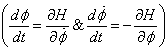 , (3.1) can be written as
, (3.1) can be written as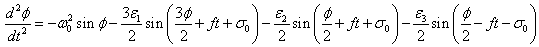 | (3.2) |
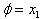 and
and 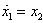 , the equation (3.1) can be written as a following system of two first order nonlinear differential equations which is treated as master system.
, the equation (3.1) can be written as a following system of two first order nonlinear differential equations which is treated as master system.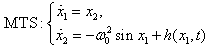 | (3.3) |
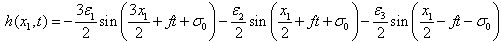 The equation of motion of DDP is given by
The equation of motion of DDP is given by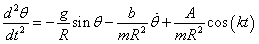 | (3.4) |
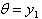 and
and 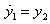 , the equation (3.4) can be written as a following system of two first order nonlinear differential equations which is treated as slave system.
, the equation (3.4) can be written as a following system of two first order nonlinear differential equations which is treated as slave system.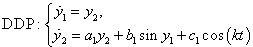 | (3.5) |
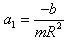 ,
, 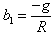 and
and 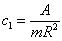 .In order to apply the RASMC to synchronize the MTS and DDP with uncertainties (0 &
.In order to apply the RASMC to synchronize the MTS and DDP with uncertainties (0 & 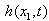 and 0 &
and 0 & 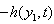 for MTS and DDP respectively), external disturbances (0 &
for MTS and DDP respectively), external disturbances (0 & 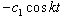 and 0 &
and 0 & 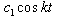 for MTS and DDP respectively) and unknown parameters (as per equation (2.10)), it is assumed that the MTS drives the DDP. The master and slave systems can be rewritten in the form of (2.1) and (2.2) as follows:
for MTS and DDP respectively) and unknown parameters (as per equation (2.10)), it is assumed that the MTS drives the DDP. The master and slave systems can be rewritten in the form of (2.1) and (2.2) as follows: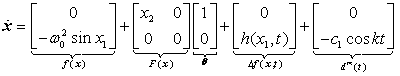 | (3.6) |
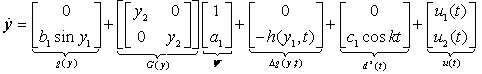 | (3.7) |
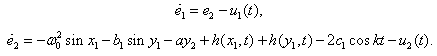 | (3.8) |
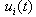 for
for 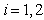 is defined as per the equation (2.11).
is defined as per the equation (2.11).4. Numerical Simulation
- In the proposed study, we have chosen
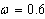 ,
, 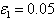 ,
, 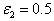 ,
, 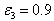 ,
, 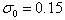 ,
, 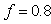 ,
, 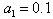 ,
, 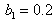 ,
, 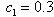 ,
, 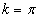 and the initial values of the update vector parameters
and the initial values of the update vector parameters 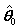 ,
, 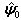 ,
, 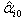 and
and 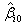 are
are 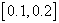 ,
, 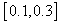 ,
, 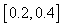 and
and 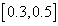 respectively. Furthermore, The vector of switching gains
respectively. Furthermore, The vector of switching gains 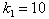 ,
, 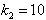 , the coefficient
, the coefficient 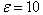 and the sliding surfaces are
and the sliding surfaces are 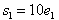 and
and 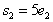 . The MTS and DDP are started with the initial conditions as follows:
. The MTS and DDP are started with the initial conditions as follows: 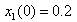 ,
, 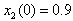 ,
, 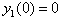 and
and 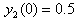 . Figure 2 illustrates the synchronization errors of the MTS and DDP, as one can see the synchronization errors converge to the zero, which implies that the chaos synchronization between the MTS and DDP is realized. The time responses of the update vector parameters
. Figure 2 illustrates the synchronization errors of the MTS and DDP, as one can see the synchronization errors converge to the zero, which implies that the chaos synchronization between the MTS and DDP is realized. The time responses of the update vector parameters 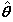 ,
, 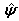 ,
, 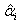 and
and 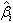 are depicted in Figures 3–6, respectively. It is very well clear that all of the update parameters approach to some constants. Furthermore, figures 7 & 8 depict the time series of state vectors of the master and slave systems and phase plots of master and slave systems have been taken in figure 9, all of that also confirm the robust synchronization between the systems under consideration. Lastly in figure 10, we have plotted the graph of the derivative of Lyapunov function (2.12) which is less than or equal to zero for t is bigger than or equal to zero
are depicted in Figures 3–6, respectively. It is very well clear that all of the update parameters approach to some constants. Furthermore, figures 7 & 8 depict the time series of state vectors of the master and slave systems and phase plots of master and slave systems have been taken in figure 9, all of that also confirm the robust synchronization between the systems under consideration. Lastly in figure 10, we have plotted the graph of the derivative of Lyapunov function (2.12) which is less than or equal to zero for t is bigger than or equal to zero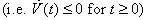 .
.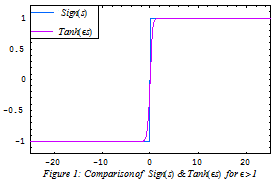 | Figure 1. Comparison of sign(s) & Tanh(εs) for ε>1 |
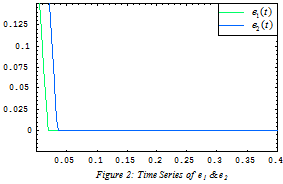 | Figure 2. Time series of e1 & e2 |
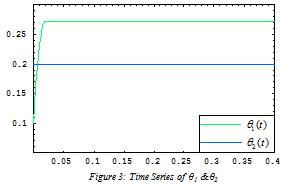 | Figure 3. Time series of θ1 & θ2 |
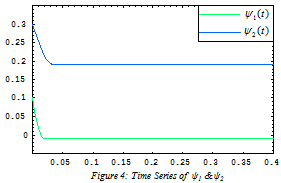 | Figure 4. Time series of Ψ1&Ψ2 |
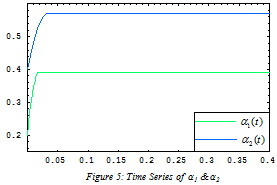 | Figure 5. Time series of α1&α2 |
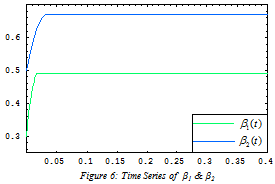 | Figure 6. Time series of β1 &β2 |
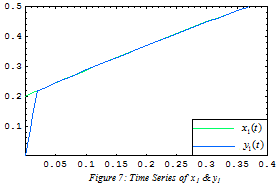 | Figure 7. Time series of χ1 & y1 |
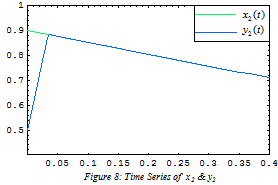 | Figure 8. Time series of x2 & y2 |
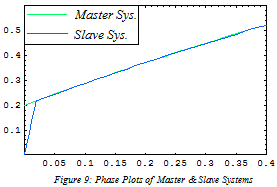 | Figure 9. Phase plots of master &slave systems |
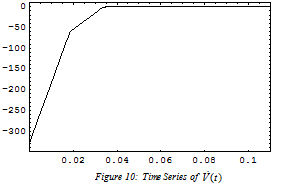 | Figure 10. Time Series of 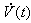 |
5. Conclusions
- In this paper, the problem of practical synchronization of chaotic systems is done using RAMSC under the effects of the model uncertainties, external disturbances and unknown parameters in synchronizing the two nonidentical chaotic systems (MTS & DDP). Numerical simulations are presented to show the applicability and feasibility of the proposed study using Mathematica. We conclude the following three remarkable features of our proposed study.(1) It is robust with respect to the model uncertainties, external disturbances and unknown parameters.(2) It can be easily realized and implemented in real world applications without requiring the bounds of the model uncertainties, external disturbances and unknown parameters to be known in advance.(3) It is well applicable for practical synchronization of two non-identical chaotic systems even when both master and slave chaotic systems are disturbed by the model uncertainties, external disturbances and unknown parameters.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML