-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(2): 58-63
doi: 10.5923/j.ajcam.20120202.11
A Generalization and Study of New Mock Theta Functions
Bhaskar Srivastava
Department of Mathematics and Astronomy, Lucknow University, Lucknow, India
Correspondence to: Bhaskar Srivastava , Department of Mathematics and Astronomy, Lucknow University, Lucknow, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Two sets of mock theta functions were developed, one by Andrews and the other by Bringmann et al. We have given two generalizations and shown they belong to the class of -functions. Relations between these generalized functions is established. Later we give q-Integral representation and multibasic expansions of these generalized -functions.
Keywords: Mock theta function, q-Multibasic expansion and q-Integral
Article Outline
1. Brief History of Mock Theta Functions
- Ramanujan in his last letter to Hardy, dated January 12, 1920, to be specific [18, pp. 354-355] gave a list of seventeen functions which he called “mock theta functions”. The functions are of a complex variable q defined by a q-series convergent for q < 1. As q approaches a root of unity. Ramanujan stated, they have certain asymptotic properties, similar to the properties of theta functions, but he conjectured that they are not theta functions. He also stated some identities relating some of the functions to each other. The list was divided into four group of functions of order three, five, five and seven. Watson[23] studied the third order mock theta functions and introduced three new one. Watson proved that the third order functions have asymptotic properties, as stated by Ramanujan and also that they are not theta functions. Watson proved the asymptotic formula, for the fifth order mock theta functions and Selberg for the seventh order mock theta functions, but neither author proved that the functions are not theta functions.In 1976, Andrews discovered “Lost” Notebook while visiting Trinity College, Cambridge in the mathematical library of the college, written by Ramanujan towards the end of his life. In the “lost” notebook were six more mock theta functions and linear relations between them, Andrews and Hickerson [6] called them of sixth order. On the page 9 of the “Lost” Notebook appears four more mock theta functions, which were called by Choi [9] of tenth order.Gordon and McIntosh, listed eight functions and called them of eighth order. Later in their survey paper [12] called only four functions of eighth order, the other four were of lower order. Hikami [13] in his work on Mathematical Physics Quantum Invariant of three manifold came across a mock theta function and called it of second order.Recently in his path breaking paper [5] while studying the q-orthogonal polynomials found some new mock theta functions. The following two mock theta functions are interesting
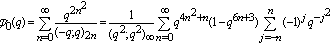
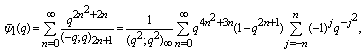
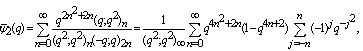 and
and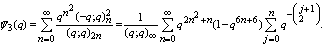 Bringmann, Hikami and Lovejoy [8] also found two more new mock theta functions
Bringmann, Hikami and Lovejoy [8] also found two more new mock theta functions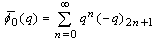 and
and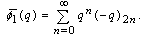 In this paper we have given two generalizations of these mock theta functions and have shown they belong to the family of Fq -functions. Being Fq -functions they have unified properties, for example:(i) The inverse operator
In this paper we have given two generalizations of these mock theta functions and have shown they belong to the family of Fq -functions. Being Fq -functions they have unified properties, for example:(i) The inverse operator 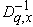 of q-differentiation is related to q-integration as(ii)
of q-differentiation is related to q-integration as(ii) 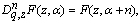 where n is a non-negative integer.The scheme of the paper is as follows: We define a Fq -function in section 3. The definition of one generalization of these mock theta functions is in section 4.Section 5 contains relations between these generalized functions.In section 6 we define a second generalization of these functions and show they are Fq -functions.Section 7 contains more relations between these generalized functions.In section 8 the generalized Fq -functions are represented as q-Integrals.In section 9, multibasic expansions are given for these generalized Fq -functions.
where n is a non-negative integer.The scheme of the paper is as follows: We define a Fq -function in section 3. The definition of one generalization of these mock theta functions is in section 4.Section 5 contains relations between these generalized functions.In section 6 we define a second generalization of these functions and show they are Fq -functions.Section 7 contains more relations between these generalized functions.In section 8 the generalized Fq -functions are represented as q-Integrals.In section 9, multibasic expansions are given for these generalized Fq -functions. 2. Basic Facts
- We shall use the following usual basic hypergeometric notations : For qk < 1,
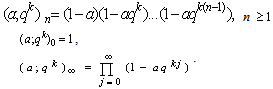 For convenience we shall write
For convenience we shall write 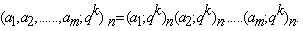 When k=1, we usually write (a)n and (a)∞ instead of (a;q)n and (a;q)∞, respectively.
When k=1, we usually write (a)n and (a)∞ instead of (a;q)n and (a;q)∞, respectively. 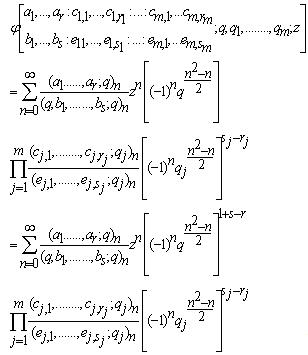 .A generalized basic hypergeometric series with base q1 is defined as
.A generalized basic hypergeometric series with base q1 is defined as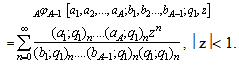
3. Definition of Fq-Functions
- Truesdell [22] in his book, “Unified theory of special functions” calls a function F-function, if it satisfies the functional equation
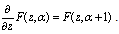 The q-analogue is: A function is called Fq -Function if it satisfies the functional equation
The q-analogue is: A function is called Fq -Function if it satisfies the functional equation 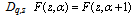 ,where
,where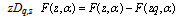 .
.4. Generalization of Mock Theta Functions and are Fq -Functions
- We give a generalization of these mock theta functions and show they are Fq -functions.Definition of the generalized functions:
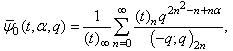 | (4.1) |
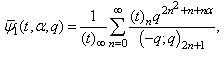 | (4.2) |
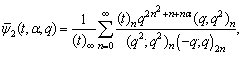 | (4.3) |
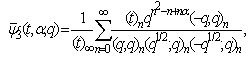 | (4.4) |
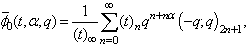 | (4.5) |
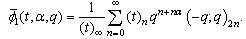 | (4.6) |
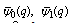
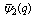 and
and 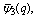 respectively. For t = 0,
respectively. For t = 0, 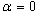 the generalized functions defined in (4.5)-(4.6) reduce to the mock theta functions
the generalized functions defined in (4.5)-(4.6) reduce to the mock theta functions 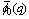 and
and 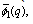 respectively.Theorem 1
respectively.Theorem 1 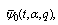
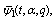
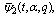
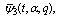
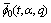 and
and 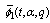 are Fq -functions.We shall give the proof for
are Fq -functions.We shall give the proof for 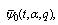 only. The proofs for the other functions are similar, hence omitted.ProofApplying the difference operator Dq,t , we have
only. The proofs for the other functions are similar, hence omitted.ProofApplying the difference operator Dq,t , we have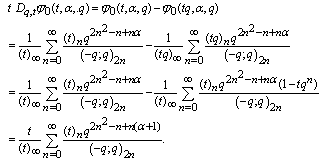 So
So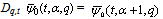 Hence
Hence 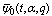 is a Fq -function. By similar working all the generalized functions given in Theorem 1 are Fq -functions.
is a Fq -function. By similar working all the generalized functions given in Theorem 1 are Fq -functions. 5. Relation between the Generalized Fq -functions 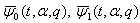 and
and 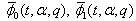
- Theorem 2
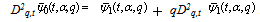 | (5.1) |
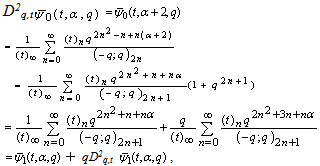 which proves Theorem 2.Theorem 3
which proves Theorem 2.Theorem 3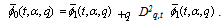 | (5.2) |
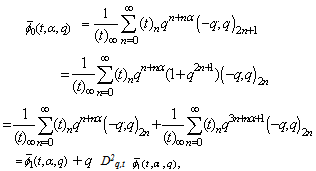 which proves Theorem 3.
which proves Theorem 3.6. Another Generalization of 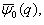
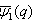 and are Fq -functions
and are Fq -functions
- We now give another generalization for
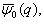
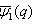 and define :
and define :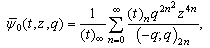 | (6.1) |
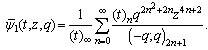 | (6.2) |
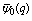 and
and 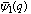 respectively.By taking
respectively.By taking 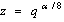 in (6.1) and (6.2), it can be shown, as is done in section 4, that they are Fq -functions.
in (6.1) and (6.2), it can be shown, as is done in section 4, that they are Fq -functions. 7. Relations between Generalized Functions
- Theorem 4
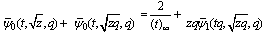 | (7.1) |
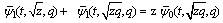 | (7.2) |
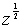 for z in (6.1) and (6.2), we have
for z in (6.1) and (6.2), we have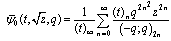 andSo
andSo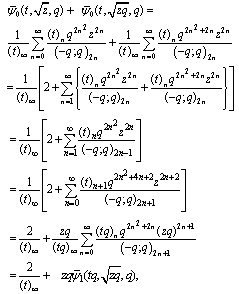 which is (7.1).Again
which is (7.1).Again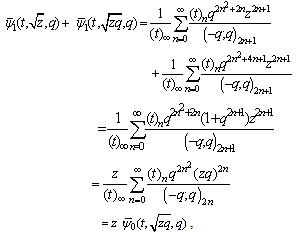 which is (7.2).Theorem 5
which is (7.2).Theorem 5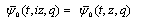 | (7.3) |
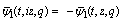 | (7.4) |
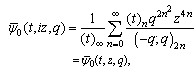 which is (7.3).Again
which is (7.3).Again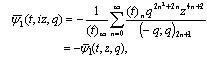 which is (7.4).
which is (7.4).8. q-Integral Representation for the Generalized Fq -functions
- The q-integral was defined by Thomae and Jackson [11, p. 19] as
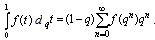 Theorem 6(i)
Theorem 6(i) 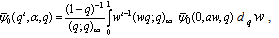 (ii)
(ii) 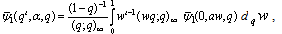 (iii)
(iii) 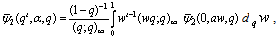 (iv)
(iv) 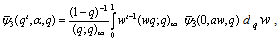 (v)
(v) 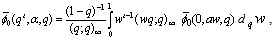 (vi)
(vi) 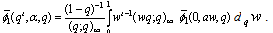 ProofWe give a detailed proof of Theorem 6(i) only. The proofs for Theorem 6 (ii)-6(vi) are on the same line, hence omitted.Limiting case of q-beta integral [ 11, p.19 (1.11.7)] is
ProofWe give a detailed proof of Theorem 6(i) only. The proofs for Theorem 6 (ii)-6(vi) are on the same line, hence omitted.Limiting case of q-beta integral [ 11, p.19 (1.11.7)] is 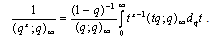 | (8.1) |
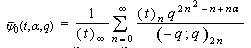 Replacing t by qt and qα by a, we have
Replacing t by qt and qα by a, we have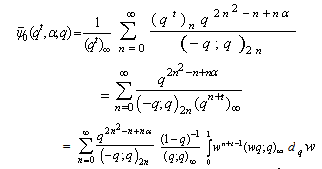 by (8.1)
by (8.1)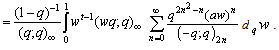 | (8.2) |
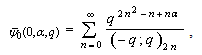 and since qα=a,
and since qα=a, 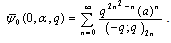 Hence
Hence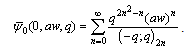 | (8.3) |
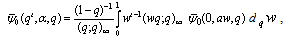 which proves (i).
which proves (i).9. Multibasic q-Hypergeometric Series Expansions for Generalized Functions
- We shall be using the following summation formula [11, (3.6.7), p. 71] and [17, Lemma 10, p. 57] in writing the multibasic expansions of the generalized functions:
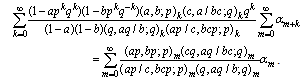 | (9.1) |
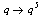 and
and  in (9.1), we have
in (9.1), we have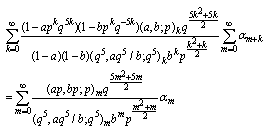 | (9.2) |
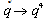 and
and 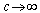 in (9.1), we have
in (9.1), we have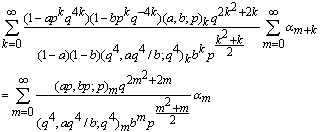 | (9.3) |
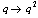 and
and 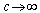 in (9.1), we have
in (9.1), we have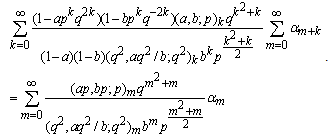 | (9.4) |
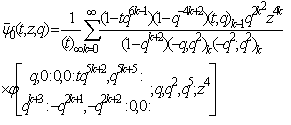 (ii)
(ii) 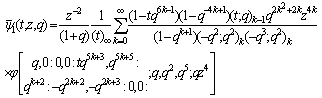 (iii)
(iii) 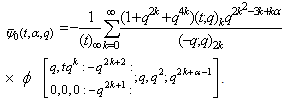 (iv)
(iv) 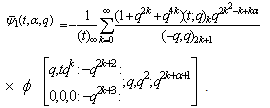 (v)
(v) 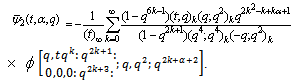 (vi)
(vi)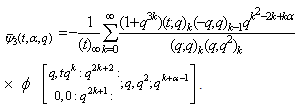 Proof of (i)We shall give the proof for
Proof of (i)We shall give the proof for 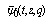 in detail, for other functions we shall only give the value of the parameters .Taking
in detail, for other functions we shall only give the value of the parameters .Taking 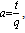 b=q2,p=q and
b=q2,p=q and 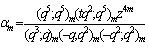 in (9.2), we have
in (9.2), we have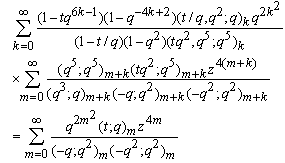 | (9.5) |
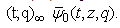 The left hand side of (9.5) is equal to which proves (i).Proof of (ii)Take
The left hand side of (9.5) is equal to which proves (i).Proof of (ii)Take 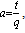 , b=q2, p=q and
, b=q2, p=q and 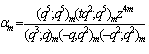 in (9.2). Proof of (iii)Letting
in (9.2). Proof of (iii)Letting 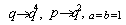 and
and 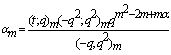 in (9.3).Proof of (iv)Letting
in (9.3).Proof of (iv)Letting 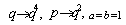 and
and 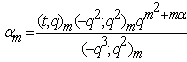 in (9.3).Proof of (v)Letting
in (9.3).Proof of (v)Letting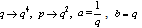 and
and 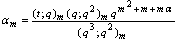 in (9.3).Proof of (vi)Letting
in (9.3).Proof of (vi)Letting 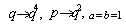 and
and 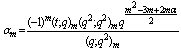 in (9.4).
in (9.4).10. Conclusions
- I have given two generalizations of these mock theta functions and shown they are Fq -functions, so they satisfy the properties of the general class of Fq -functions. The generalization helps in giving relationship between these functions. Apart from these values, we can give other values to have another set of functions having these properties. I think these relations may yield interesting results in the theory of partitions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML