-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(2): 55-57
doi:10.5923/j.ajcam.20120202.10

A Suggested Approach for Solving Weighted Goal Programming Problem
Maged G. Iskander
The British University in Egypt, Department of Business Administration, Postal No. 11837, P.O. Box 43, El Sherouk City, Egypt
Correspondence to: Maged G. Iskander , The British University in Egypt, Department of Business Administration, Postal No. 11837, P.O. Box 43, El Sherouk City, Egypt.
| Email: |  |
Copyright © 2012 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the weighted goal program is reformulated as a lexicographic weighted goal program with two main goals. The first goal, which has the first priority, seeks to minimize the maximum weighted undesired normalized deviation. The second goal, having the second priority, minimizes the sum of the undesired normalized (or weighted normalized) deviations. This approach aims to provide a solution that is consistent with the weighting scheme. The suggested approach is illustrated by a numerical example.
Keywords: Weighted Goal Programming, Lexicographical Goal Programming, Min-Max Weighted Normalized Deviation
Cite this paper: Maged G. Iskander , A Suggested Approach for Solving Weighted Goal Programming Problem, American Journal of Computational and Applied Mathematics , Vol. 2 No. 2, 2012, pp. 55-57. doi: 10.5923/j.ajcam.20120202.10.
Article Outline
1. Introduction
- Goal programming, as one of the multiple-objective techniques, is commonly used when there are multiple conflicting goals. Many attempts have been made in the field of goal programming [8]. When the goals are based on a pre-emptive priority structure, then the lexicographical goal programming is utilized [1] and [6]. In many applications, the decision-maker may not require achieving his/her goals according to a priority rank structure, since the achievement of the goals having high priority levels might seriously affect the achievement of the goals with lower priority levels. Moreover, in lexicographical goal programs, the solution may not be practically applicable. In this case, the undesired deviations of the goals are weighted by relative weights that present the decision-maker preferences between different goals. The preferential weights associated with the non-normalized deviational variables may cause interpretation difficulties for the decision-maker [4].The basic structure of the additive weighted goal program is to minimize the objective function, which takes a mathematical expression of the sum of the weighted undesired deviations [7]. Minimizing the additive weighted objective function needs the undesired deviations to be normalized in order to remove the effect of high aspiration levels on the solution. However, the solution of the normalized additive weighted goal program may not necessarily match the weighting preferences. On the other hand, the decision-maker may not be able to set his/her own weighting scheme. Therefore, a systematic technique for weight space analysis was developed [2]. A recent weight sensitivity algorithm for investigating a portion of weight space of interest to the decision-maker in goal programming has been presented by Jones [3]. In many cases, the decision-maker would like to stick to a certain weighting scheme and to get a solution that matches, as much as possible, with his/her weight preferences. In this case, the proposed approach can be utilized. This approach is presented in the next section. Section 3 illustrates the suggested approach by a numerical example. Finally, Section 4 draws conclusions.
2. The Suggested Weighted Goal Programming Approach
- Consider the following normalized linear goal constraints:
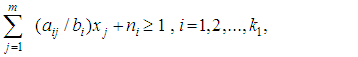 | (1) |
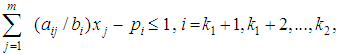 | (2) |
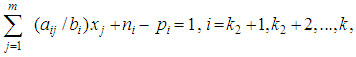 | (3) |
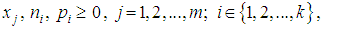 | (4) |
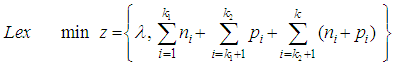 | (5) |
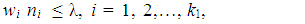 | (6) |
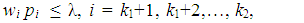 | (7) |
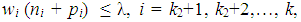 | (8) |
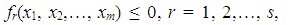 | (9) |
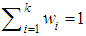 , represent the preference scheme, which is the desirable achievement relation between the goal constraints. On the other hand, a set of s system constraints is given by (9). In the next section, the suggested approach is illustrated by a numerical example.
, represent the preference scheme, which is the desirable achievement relation between the goal constraints. On the other hand, a set of s system constraints is given by (9). In the next section, the suggested approach is illustrated by a numerical example.3. Illustrative Example
- The suggested approach is illustrated by the first numerical example used by Jones [3], which is related to a hypothetical manufacturing situation. His normalized weighted goal program consists of four goals and two system constraints, in addition to the non-negativity constraint. Therefore, the suggested normalized goal program can be stated as follows:
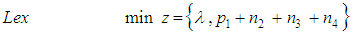
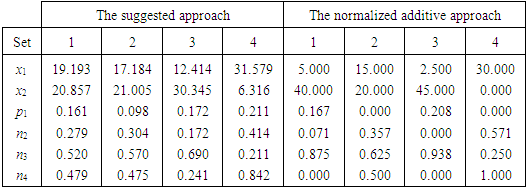
 The model is solved by using the relative weights of the four distinct solutions that have been produced according to Jones’ revised weight sensitivity analysis algorithm. The four sets of relative weights are: {0.455, 0.263, 0.141, 0.141}, {0.600, 0.193, 0.103, 0.103}, {0.400, 0.400, 0.100, 0.100}, and {0.400, 0.100, 0.400, 0.100}. The results of the suggested approach are compared with those of the normalized additive approach. Table 1 presents the results of the four sets of relative weights.In general, the main criterion is that the normalized deviation of the goal with high relative weight should be less than that of the goal with low relative weight. However, the goals with the same weight may have different normalized deviations, especially when this weight is relatively small. This criterion is satisfied in the suggested approach for each of the four sets of relative weights, while it is violated in the case of the normalized additive approach for sets 1 and 3. Although, for sets 2 and 4, this criterion is satisfied in the normalized additive approach, the sum of the normalized deviations for each of these two sets is greater than its corresponding one in the case of the suggested approach. On the other hand, most of the results of the suggested approach verify Proposition 1.Finally, since Jones’ algorithm can be used to investigate a portion of weight space of interest to the decision-maker, then the suggested approach may be applied using these weights in order to get better solutions, especially if the decision-maker could not set his/her own fixed relative weights.
The model is solved by using the relative weights of the four distinct solutions that have been produced according to Jones’ revised weight sensitivity analysis algorithm. The four sets of relative weights are: {0.455, 0.263, 0.141, 0.141}, {0.600, 0.193, 0.103, 0.103}, {0.400, 0.400, 0.100, 0.100}, and {0.400, 0.100, 0.400, 0.100}. The results of the suggested approach are compared with those of the normalized additive approach. Table 1 presents the results of the four sets of relative weights.In general, the main criterion is that the normalized deviation of the goal with high relative weight should be less than that of the goal with low relative weight. However, the goals with the same weight may have different normalized deviations, especially when this weight is relatively small. This criterion is satisfied in the suggested approach for each of the four sets of relative weights, while it is violated in the case of the normalized additive approach for sets 1 and 3. Although, for sets 2 and 4, this criterion is satisfied in the normalized additive approach, the sum of the normalized deviations for each of these two sets is greater than its corresponding one in the case of the suggested approach. On the other hand, most of the results of the suggested approach verify Proposition 1.Finally, since Jones’ algorithm can be used to investigate a portion of weight space of interest to the decision-maker, then the suggested approach may be applied using these weights in order to get better solutions, especially if the decision-maker could not set his/her own fixed relative weights.
|
4. Conclusions
- The paper presents a suggested approach to solve normalized weighted goal programming problems. This approach firstly minimizes the maximum weighted normalized deviational variable, while secondly minimizes the sum of the normalized (or weighted normalized) deviational variables. The proposed approach seeks to provide a solution in which the normalized non-achievements of goals are inversely proportional to the relative weights. If the decision-maker could not set his/her preferences in terms of specific relative weights, then Jones’ algorithm can be utilized before applying the suggested approach.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML