-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2016; 6(1A): 7-13
doi:10.5923/s.ijee.201601.02

Charateristic of Walter’s B Visco-Elastic Nanofluid Layer Heated from Below
S. D. Pandey 1, V. K. Nema 2, Sanddep Tiwari 3
1Faculty of Engineering, KNIPSS, Sultanpur, India
2G.R.D.K. Institute of Science and Technology, Jabalpur, India
3AIMT, Gr. Noida, India
Correspondence to: S. D. Pandey , Faculty of Engineering, KNIPSS, Sultanpur, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The onset of convection in a horizontal layer of Walter’s B' visco-elastic nanofluid is studied. A linear stability analysis based upon normal mode analysis is used to find solution of the fluid layer confined between two free boundaries. The onset criterion for stationary and oscillatory convection was derived analytically and graphically. The effects of the concentration Rayleigh number, Prandtl number, capacity ratio, Lewis number and kinematics visco elasticity Parameter on the stability of the system are investigated both on stationary and oscillatory convection. The sufficient conditions for the non-existence of oscillatory convection were also obtained.
Keywords: Thermal Instability, Nanofluid, Walter’s B' Visco- Elastic, Oscillatory Convection
Cite this paper: S. D. Pandey , V. K. Nema , Sanddep Tiwari , Charateristic of Walter’s B Visco-Elastic Nanofluid Layer Heated from Below, International Journal of Energy Engineering, Vol. 6 No. 1A, 2016, pp. 7-13. doi: 10.5923/s.ijee.201601.02.
Article Outline
1. Introduction
- Nanofluid have novel properties that make them potentially useful in many applications in heat transfer, including microelectronics, fuel cells, pharmaceutical processes, and hybrid powered engines, domestic refrigerator, chiller, heat exchanger and nuclear reactor, in grinding, in machining, in space, defense and ships, and in boiler flue gas temperature reduction. Nanofluid is a fluid colloidal mixture of nano (<100 nm) sized particles, in base fluid. Nanoparticles materials may be taken as oxide ceramics (Al2O3, CuO), metal carbides (SiC), nitrides (AlN, SiN) or metals (Al, Cu) etc. and base fluids are water, ethylene or tri-ethylene- glycols and other coolants, oil and other lubricants, bio-fluids, polymer solutions, other common fluids. The term ‘nanofluid’ was coined by Choi [1]. Since Choi proposed his theory on nanofluids a continuous effort has ensued to look for the causes of the so-called anomalous increase in thermal conductivity of nanofluids. The presence of nanoparticles in the fluid significantly increases the effective thermal conductivity of the mixture. Buongiorno [2] noted that the nanoparticles absolute velocity can be viewed as the sum of the base fluid velocity and a relative (slip) velocity. He also discussed the effect of seven slip mechanisms: Inertia, Brownian diffusion, Thermophoresis, Diffusiophoresis, Magnus effect, Fluid drainage and Gravity setting. He concludes that in the absence of turbulent eddies Brownian diffusion and thermophoresis dominate the other slip mechanisms. Xuan and Li [3] investigated convective heat transfer and flow features of Cu-water nanofluid. They observed that the suspended nanoparticles remarkably enhance heat transfer process and the nanofluid has larger heat transfer coefficient than that of the original base liquid under the same Reynolds number. The heat transfer feature of a nanofluid increases with volume fraction of nanoparticles. A detail account of the thermal instability of Newtonian fluids has been discussed in detail by Chanderasekher [4]. The Bénard problem (the onset of convection in a horizontal layer uniformly heated from below) for a nanofluid was studied by many authors [5-16]. The above study deals with nanofluid as Newtonian fluid. There is growing importance of non-Newtonian fluids in geophysical fluid dynamics, chemical technology, petroleum, biological and material industries. The study of non-Newtonian nanofluid is desirable. Bhatia and Steiner [17] studied the thermal instability of visco-elastic fluids. An experimental demonstration by Toms et al. [18] has revealed that a dilute solution of methyl methacrylate in n-butyl acetate agrees well with the theoretical model of Oldroyd [19]. There are many visco-elastic fluids which cannot be characterized by Maxwell’s constitutive relations. Two such classes of elastico-viscous fluids are Rivlin-Ericksen and Walters’ (Model B') fluids. Walters [20] reported that the mixture of polymethyl methacrylate and pyridine at 25C containing 30.5g of polymer per litre with density 0.98g per litre behaves very nearly as the Walters’ (Model B') fluid. Walters’ (Model B') visco- elastic fluid forms the basis for the manufacture of many important polymers and useful products. Sharma et al. [21] have studied the stability of two superposed Walters’ (Model B') liquids whereas thermosolutal convection problem in the presenceof magnetic field for Walters’ (Model B') fluid has been investigated by Sunil et al. [22]. The interest for investigations of visco-elastic nanofluids is also motivated by a wide range of engineering applications which include ground pollutions by chemicals which are non-Newtonian like lubricants and polymers and in the treatment of sewage sludge in drying beds. Recently, polymers are used in agriculture, communications appliances and in bio medical applications. In the present study, we investigated the thermal instability of a visco-elastic (Model B') nanofluid fluid.
2. Mathematical Formulations
- Consider an infinite horizontal layer of Walter’s B’ elastico-viscous nanofluid of thickness‘d’ bounded by plane z = 0 and z = d and heated from below. Each boundary wall is assumed to be impermeable and perfectly thermal conducting. Fluid layer is acted upon by gravity force g(0, 0, -g). The temperature T and volumetric fraction φ of nano particles at z = 0 taken to be T0 and φ0 at z = 0 and T1 and φ1 at z = d, (T0 > T1). The reference temperature is taken to be T1. Thermo physical properties of the nano fluid are constant for the analytical formulation but these properties are not constant and strongly depend upon volume fraction of the nano particles. Thus the governing equations for Walter’s B' elastico-viscous nanofluid are
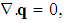 | (1) |
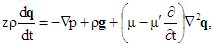 | (2) |
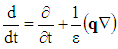 stands for convection derivative, q(u, v, w) is the velocity vector, p is the hydrostatic pressure, μ is viscosity, μ' kinematic visco-elasticity and g(0, 0, -g) is acceleration due to gravity.The ρ density of the nanofluid can be written as Buongiorno2
stands for convection derivative, q(u, v, w) is the velocity vector, p is the hydrostatic pressure, μ is viscosity, μ' kinematic visco-elasticity and g(0, 0, -g) is acceleration due to gravity.The ρ density of the nanofluid can be written as Buongiorno2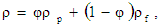 | (3) |
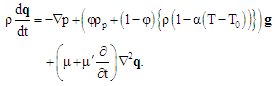 | (4) |
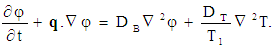 | (5) |
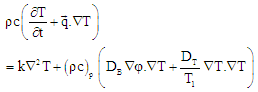 | (6) |
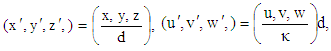
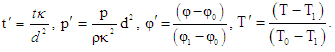 where
where 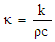 is thermal diffusivity of the fluid. There after dropping the dashes (') for simplicity.
is thermal diffusivity of the fluid. There after dropping the dashes (') for simplicity.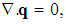 | (7) |
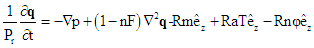 | (8) |
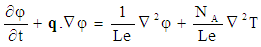 | (9) |
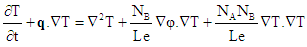 | (10) |
|
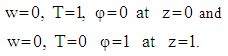 | (12) |
2.1. Basic Solutions
- The basic state was assumed to be quiescent and is given by:
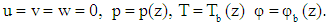 | (13) |
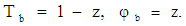 | (14) |
2.2. Perturbation Solutions
- To study the stability of the system, we superimposed infinitesimal perturbations on the basic state, which are of the forms
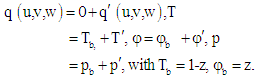 | (15) |
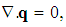 | (16) |
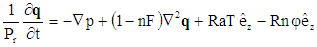 | (17) |
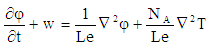 | (18) |
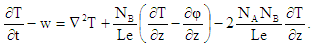 | (19) |
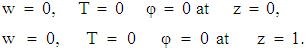 | (20) |
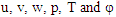 can be reduced to three by operating equation (17) with
can be reduced to three by operating equation (17) with  we get
we get 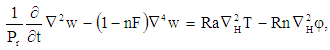 | (21) |
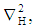 is two-dimensional Laplacian operator.
is two-dimensional Laplacian operator. 3. Normal Modes
- Analyzing the disturbances into the normal modes and assuming that the perturbed quantities are of the form
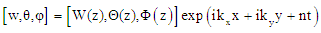 | (22) |
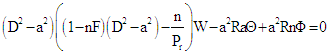 | (23) |
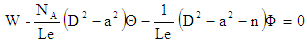 | (24) |
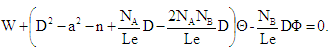 | (25) |
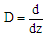 and
and 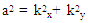 is dimensionless the resultant wave number.The boundary conditions for free-free boundaries surfaces are thus
is dimensionless the resultant wave number.The boundary conditions for free-free boundaries surfaces are thus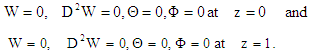 | (26) |
4. Linear Stability Analysis
- The solution to be W, Θ and Ф is of the form
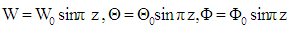 | (27) |
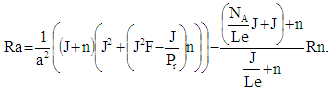 | (28) |
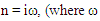 is real and dimensional frequency) in equation (28), we get
is real and dimensional frequency) in equation (28), we get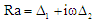 | (29) |
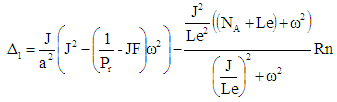 | (30) |
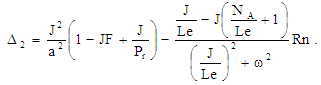 | (31) |
4.1. Stationary Convection
- For stationary convection
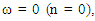 equation (29) reduces to
equation (29) reduces to 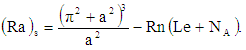 | (32) |
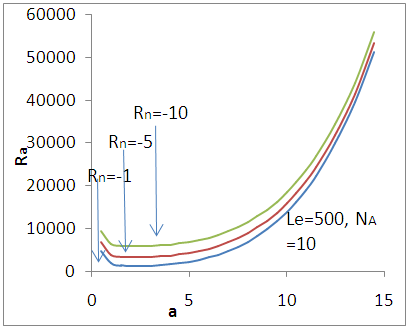
 | Figure 1. Variation of stationary Rayleigh number Ra with wave number - a for different values concentration Rayleigh number |
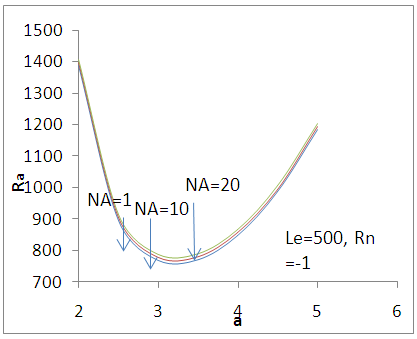 | Figure 2. Variation of stationary Rayleigh number Ra with wave number - a for different values of modified diffusivity ratio |
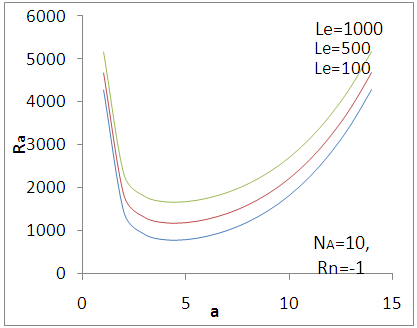
 | Figure 3. Variation of stationary Rayleigh number Ra with wave number- a for different values of Lewis number Le |
4.2. Oscillatory Convection
- For oscillatory convection ω # 0, we must have Δ2 = 0, which gives
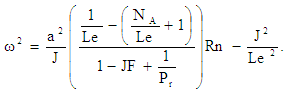 | (33) |
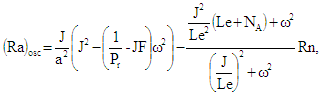 | (34) |
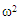 is given by equation (33). If
is given by equation (33). If 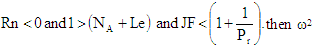 is negative and hence oscillatory convection cannot occur. Thus for
is negative and hence oscillatory convection cannot occur. Thus for 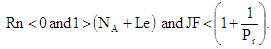 are sufficient conditions for the non-existence oscillatory convection, the violation of which does not necessarily imply the occurrence of oscillatory convection.
are sufficient conditions for the non-existence oscillatory convection, the violation of which does not necessarily imply the occurrence of oscillatory convection.5. Results and Discussions
- Expression for stationary thermal Rayleigh number is given in equation (32) and for oscillatory thermal Rayleigh number is given in equation (34). We have discussed our results graphically.Figure 4 shows the variation of oscillatory Rayliegh number Ra with wave number a for different value of kinematic visco-elasticity parameter F and it is found that oscillatory Rayliegh number Ra decreases with increases in the values of kinematic visco-elasticity parameter F, thus kinematic visco-elasticity parameter F have destabilzing effect on the oscillatory convection.
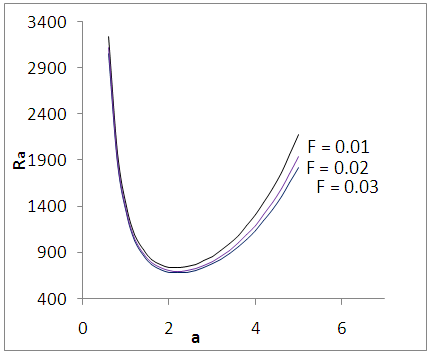 | Figure 4. Variation of oscillatory Rayliegh number Ra with wave number - a for different concentration Rayleigh number |
 | Figure 5. Variation oscilltory Rayleigh number with wave number - a for different value of kinematic visco-elasticity parameter F |
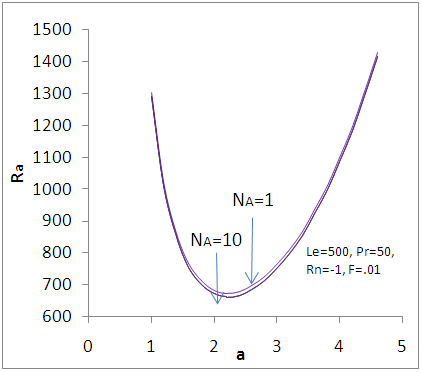
 | Figure 6. Variation of oscillatory Rayliegh number with wave number - a for different modified diffusivity ratio |
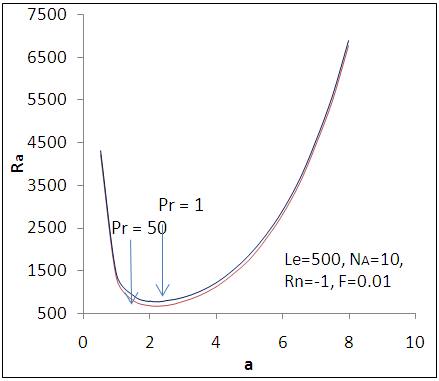
 | Figure 7. Variation of oscillatory Rayliegh number with wave number- a for different Prandtl number |
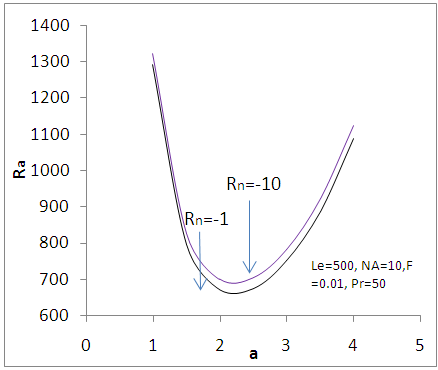
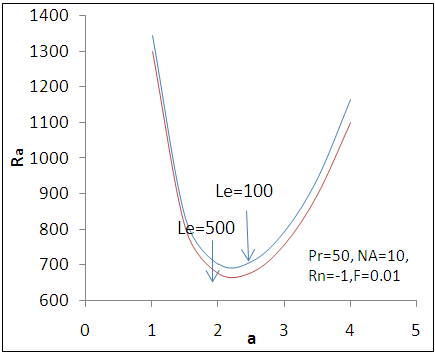 | Figure 8. Variation of oscillatory Rayliegh number with wave number - a for different Lewis number Le |
6. Conclusions
- We studied linear instability of Walter’s B' elastico-viscous nanofluid heated from below by employing a model that incorporate the effects of Brownian motion, thermophoresis and visco elasticity. An expression for Rayleigh number, for the stationary convection and oscillatory convection is obtained. We draw following conclusion:(i) The critical cell size is not a function of any thermophysical properties of nanofluid.(ii) The effect of Lewis number Le and modified diffusivity ratio NA is to stabilizes the stationary convection and destabilize s the oscillatory convection.(iii) The concentration Rayleigh number Rn destabilizes both stationary and oscillatory convection.(iv) The oscillatory convection is possible only for the bottom-heavy nanoparticles distribution while stationary convection is possible for both bottom and top-heavy distribution of nanoparticles.(v) The Prandtl number Pr destabilizes the oscillatory convection and no has effect on stationary convection.(vi) Kinematic visco-elasticity parameter F destabilizes the oscillatory convection and no has effects on stationary convection.(vii) A comparison between nano fluid and ordinary fluid made and it is found that nano fluid is more stable than ordinary fluid.(viii) It was also found that Rayleigh number in stationary convection has higher value in than that of Rayleigh number in oscillatory convection.The sufficient conditions for the non-existence of oscillatory convection are
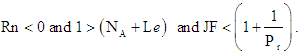
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML