-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Economics
p-ISSN: 2166-4951 e-ISSN: 2166-496X
2014; 4(2A): 73-80
doi:10.5923/s.economics.201401.06
The Demand for Money in Mexico
Raul Ibarra
Banco de México, Direccion General de Investigacion Economica, Av. 5 de Mayo 18, Centro, Mexico City, 06059, Mexico
Correspondence to: Raul Ibarra, Banco de México, Direccion General de Investigacion Economica, Av. 5 de Mayo 18, Centro, Mexico City, 06059, Mexico.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
This paper examines the demand for narrow money in Mexico for the period 1980-2005, extending the study by Khamis and Leone (2001). The cointegration analysis suggests the presence of a long term relationship between real money balances, consumption expenditures and the interest rate. The model is estimated in error correction form, indicating the existence of two additional determinants of real money balances in the short run to those found by the referred authors: changes in consumption expenditures and changes in the depreciation rate. The stability tests applied to the estimated model suggest parameter constancy throughout the examined period.
Keywords: Money demand, Cointegration, Stability
Cite this paper: Raul Ibarra, The Demand for Money in Mexico, American Journal of Economics, Vol. 4 No. 2A, 2014, pp. 73-80. doi: 10.5923/s.economics.201401.06.
Article Outline
1. Introduction
- The study of the demand for money has a central role for the conduct of monetary policy. For instance, in 1994, in order to attain price stability during the financial crisis, the Central Bank of Mexico established a reserve money target based on projections on the demand for money. This policy was based on the assumption that the demand for money remained stable during the financial crisis. However, Mexico is a country that has experienced a considerable variability in inflation, interest rates and exchange rates, which could cause possible instability in the money demand function. This paper investigates whether this function remains stable during the period 1980-2005 in Mexico. In spite of its importance for monetary policy, this issue has not usually been addressed in the relevant literature for Mexico. For example, in the study of Desentis (1997), the stability of the estimated money demand is not examined. Ramos Francia (1993) investigates the stability of the demand for M1 in Mexico, but this study extends only to 1990.The empirical evidence on the stability for the demand function is mixed. Rogers (1992) finds that there is clear no evidence of structural stability on the estimated equation during the period 1977-1985. On the other hand, Cuthbertson and Galindo (1999) find a stable money demand function for the period 1976: IV to 1990: III. In a more recent study, Khamis and Leone (2001), provide evidence of a long term cointegration relationship between real currency, real consumption and inflation rate, using monthly data for the period 1983:1-1997:6. Furthermore, the authors find that the dynamic model of real currency demand remained stable even after the financial crisis in 1994.This paper investigates whether there exists a cointegration relationship between real money, a scale variable and an opportunity cost variable, using the methodology of Johansen and Juselius (1990). The scale and opportunity cost variables are measured in different ways, following Mankiw and Summers (1986). In addition, the short run money demand is estimated in error correction form, using the general to specific methodology suggested by Hendry and Richard (1982, 1983). This paper extends the study of Khamis and Leone (2001) in several interesting ways. First, the study period includes data from 1980: I to 2005: II, which is important as we are concerned with long term relationships. Second, following the literature on this subject, this study uses quarterly rather than monthly data. This avoids the problem of repeating the same data for each month of the same quarter when monthly data are not available. Finally, this study incorporates the interest rate as a determinant of the long term money demand, which is consistent with the empirical evidence found in other countries. The results of this study suggest the presence of a long term relationship between real money balances, consumption expenditures and interest rates. The study indicates the existence of two additional determinants of real money balances in the short run to those found in Khamis and Leone (2001): changes in private expenditures and changes in the depreciation rate. The stability tests suggest parameter constancy throughout the examined period.This paper is organized as follows. Section II provides a description of the data. Section III presents unit root tests along with the results of the cointegration test between real money balances, consumption and interest rates. Section IV provides the estimated model in error correction form and the results of stability tests. Section V presents conclusions.
2. The Data
- The data for this study are obtained from the International Financial Statistics, published by the International Monetary Fund. Following previous studies on stability of money demand, this paper uses quarterly unadjusted data. The study period is from 1980: I to 2005: II. All variables are in natural logarithms, with the exception of the interest rate.In the literature of money demand, there is general agreement that in the long run, the level of real money balances is a function of a scale variable, such as income or wealth, and a measure on the opportunity cost of holding money, such as the interest rate, the inflation rate or the return on foreign assets. Because of its importance for issues of monetary policy, this study concentrates on the demand for real M1 (mt), which is defined as the sum of transferable deposits and currency outside deposit money banks. This variable is more appropriate in models that emphasize that money is used for transaction purposes. Following the arguments given in Mankiw and Summers (1986), three different scale variables are applied, real GDP (yt), real private consumption expenditures (pct) and industrial production index (ipt). Moreover, two different interest rates are used, the one month treasury bill rate (trt), and the 60-day deposit rate (drt). Money balances and consumption expenditures are deflated by Consumption Price Index, since this variable is a better determinant of transaction balances than GDP deflator, as explained by Muscatelli and Spinelli (2000).Following Khamis and Leone (2001), the exchange rate depreciation (dept) is used as a proxy variable of the return on foreign assets. Inflation (Δpt) and depreciation rate (dept) are calculated as the percent change over the previous quarter, and they are annualized.Figure 1 shows the series for real money, private consumption and interest rates. The first panel illustrates the long term relationship between real money and real consumption. The second panel shows the long term relationship between interest rates and the inverse of real money.
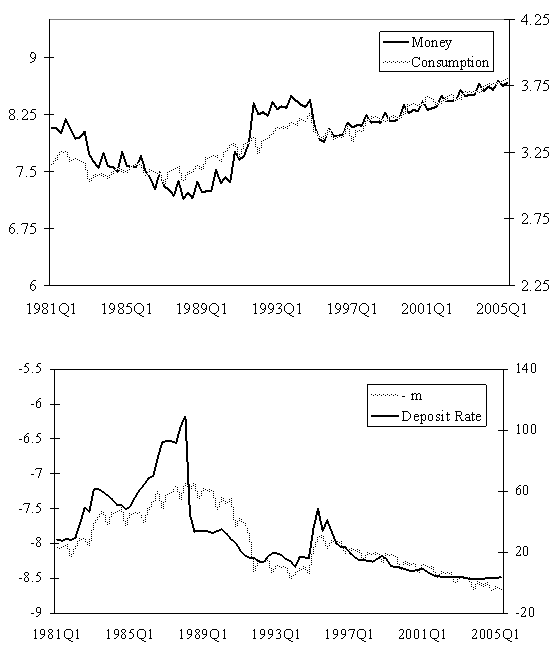 | Figure 1. Real Money, Real Consumption and Interest Rates |
3. Long Run Behavior and Cointegration
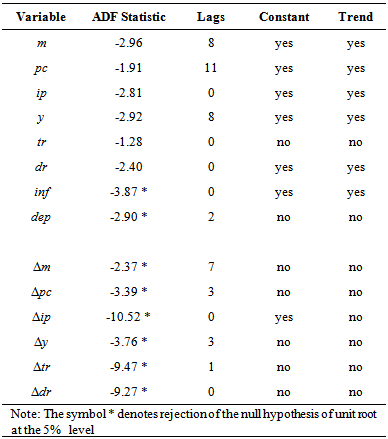
- Preliminary Tests: Unit RootsFollowing Johansen (1988), the cointegration test requires that the time series involved are integrated of order one, or equivalently, follow a unit root process. To determine the order of integration, Augmented Dickey Fuller (ADF) tests are used. The ADF test for the variable Xt is implemented by estimating the next regression:
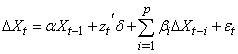 | (1) |
|
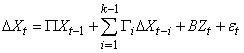 | (2) |
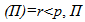 can be rewritten as
can be rewritten as 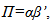 where
where 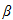 may be interpreted as a p×r matrix of cointegrating vectors and α as a p×r matrix of adjustment coefficients. Johansen (1988) estimates
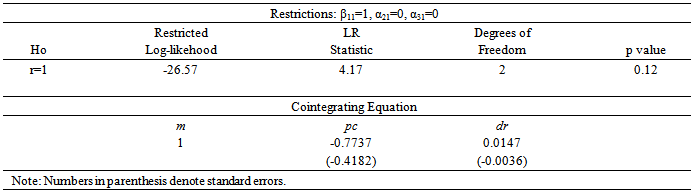
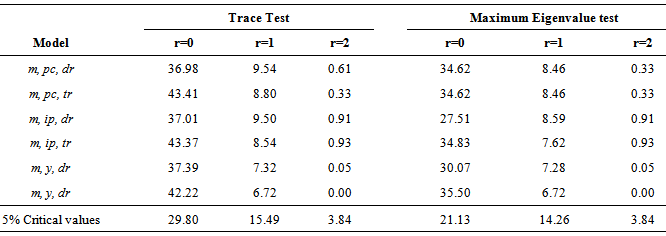
may be interpreted as a p×r matrix of cointegrating vectors and α as a p×r matrix of adjustment coefficients. Johansen (1988) estimates 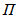 from an unrestricted VAR and provides a test statistic for the hypothesis that there are at most r cointegrating vectors. Then, Johansen (1991) develops tests statistics for the individual elements of the matrices α and β.In order to determine the number of cointegrating vectors r, two types of test statistics are used, the trace statistics and the maximum eigenvalue statistics. These tests are sequentially applied for the null hypothesis of r=0 to r=p-1 until fail to reject.Before conducting the cointegration tests, it is necessary to determine the appropriate lag length for the VAR model. To address this issue, the SIC was used. Table 2 reports the results of the cointegration tests on mt, pct and drt, allowing for linear trends in the series, seasonal dummies, a constant in the cointegrating vector and zero lags. Both the trace and the maximum eigenvalue test suggest the presence of exactly one cointegration relationship.
from an unrestricted VAR and provides a test statistic for the hypothesis that there are at most r cointegrating vectors. Then, Johansen (1991) develops tests statistics for the individual elements of the matrices α and β.In order to determine the number of cointegrating vectors r, two types of test statistics are used, the trace statistics and the maximum eigenvalue statistics. These tests are sequentially applied for the null hypothesis of r=0 to r=p-1 until fail to reject.Before conducting the cointegration tests, it is necessary to determine the appropriate lag length for the VAR model. To address this issue, the SIC was used. Table 2 reports the results of the cointegration tests on mt, pct and drt, allowing for linear trends in the series, seasonal dummies, a constant in the cointegrating vector and zero lags. Both the trace and the maximum eigenvalue test suggest the presence of exactly one cointegration relationship.
|
|
4. The Error Correction Model
- Having estimated the long run money demand, the next step is to estimate a dynamic model which contains the short run adjustment to the deviation from the long run equilibrium. In the last section, it was found that the variables pc and dr are weakly exogenous. Therefore, following Hendry (1995), the short run money demand can be estimated by using a general autoregressive distributive lag (ADL) model. This methodology starts by estimating the next general dynamic specification:
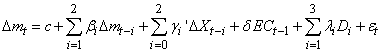 | (3) |
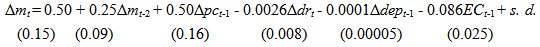 | (4) |
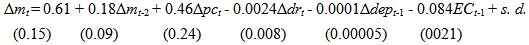 | (5) |
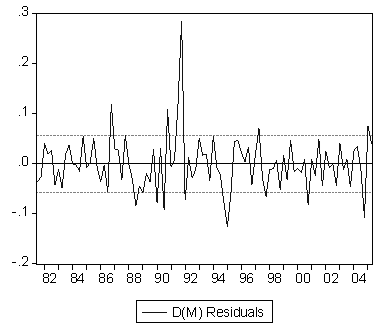 | Figure 2. Residuals of the Error Correction Model |
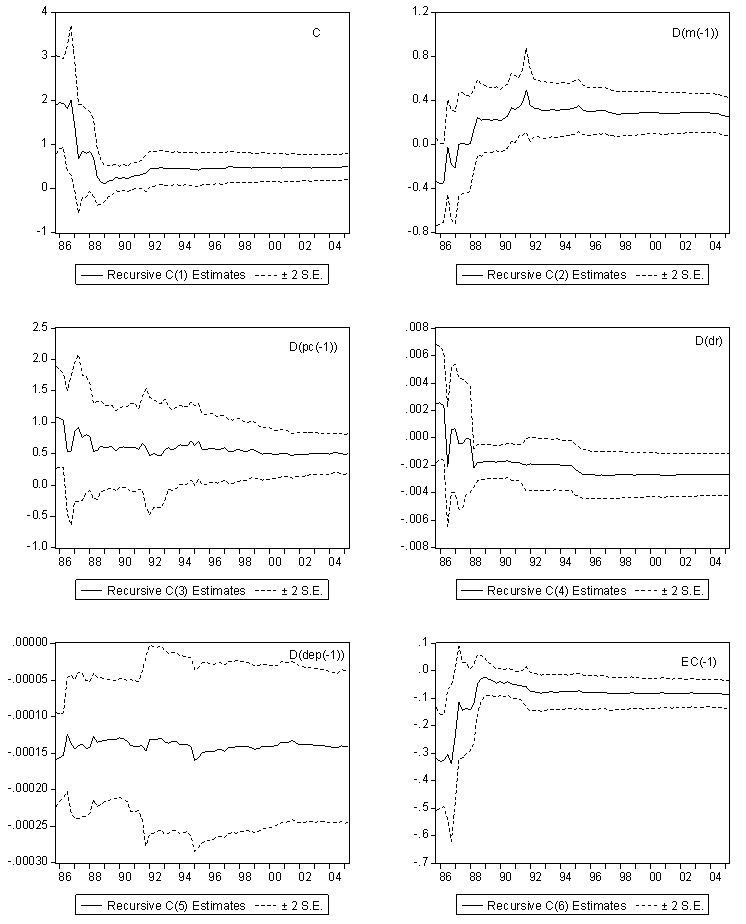 | Figure 3. Recursive Coefficient Estimates |
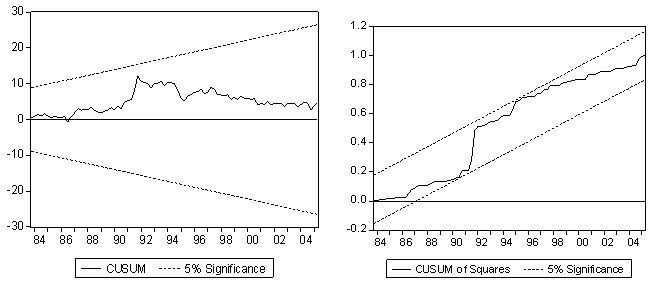 | Figure 4. CUSUM and CUSUM of Squares Tests |
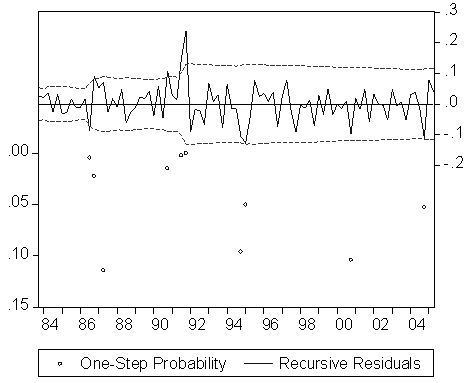 | Figure 5. One Step Residuals Test |
|
5. Conclusions
- This paper examines the demand for narrow money in Mexico for the period 1980-2005, extending the study by Khamis and Leone (2001). The cointegration tests results suggest the existence of a long term relationship between real money balances, consumption expenditures and interest rates.The estimated error correction model indicates the existence of two additional determinants of real money balances in the short run to those found in Khamis and Leone (2001): changes in private expenditures and changes in the depreciation rate. Monetary authorities should take these variables into account for making projections on money demand. The stability tests suggest parameter constancy throughout the examined period, despite the fact that Mexico has experienced important periods of crisis, substantial variability in inflation, exchange rates and interest rates.
Appendix
Notes
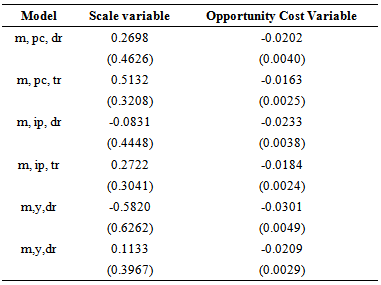
- 1. I thank Dennis Jansen for valuable comments. The views on this paper correspond to the author and do not necessarily reflect those of Banco de Mexico.2. See for example Hoffman et al (1995).3. For instance, in a study on stability of money demand in Germany, Lütkepohl et al (1999), illustrate the importance of using seasonally unadjusted data when seasonal changes may be a source of instability.4. The return on foreign assets equals the sum of the foreign interest rate plus the exchange rate depreciation rate. Following Khamis and Leone (2001), movements in the return on foreign assets are dominated by the exchange rate changes.5. It’s important to notice that the t-ratio test doesn’t follow the usual t distribution; critical values are tabulated from Monte Carlo distributions in Mac Kinnon (1996).6. For the variable pct, the null hypothesis of a unit root is rejected at the 5% significance level when the number of lags is selected according to SIC. However, when this number is selected according to the Akaike Information Criterion, the null hypothesis is not rejected. In what follows, this variable is assumed to be I(1).7. Seasonal dummy variables are centered (orthogonalized). Johansen (1995) argues that using centered seasonal dummies avoids the problem of affecting the trend of the level series when standard dummies are applied.8. The cointegration test is also examined including ipt and yt as scale variable, and trt as an opportunity cost measure. However, in two cases the sign of the coefficient on the scale variable is not as expected. For comparison purposes, the results for these tests are given in the appendix. 9. For example, Hoffman and Rasche (1991), using US data from 1953 to 1988, find a short term interest elasticity in the -0.4 to -0.6 range.10. Cuthbertson and Galindo (1999), explain that the delayed response to changes in exchange rates may occur because the exchange rate tends to move in the same direction during crisis periods, and it is generally stable during in intervening periods. Therefore, agents respond to the lagged exchange rate as the can anticipate the trend of exchange rate in the short run.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML