1. Introduction

Since cognitive radios(CR) are considered secondary users for using the licensed spectrum, a crucial requirement of cognitive radio network is that they must efficiently exploit underutilized spectrum without causing harmful interference to the Pus (primary users). Furthermore, PUs have no obligation to share and change their operating parameter for sharing spectrum with cognitive radio networks. Hence, cognitive radios should be able to independently detect spectral opportunities without any assistance form PUs. CR has emerged as one of the most promising candidate solutions to improve spectrum utilization in next generation cellular networks [1]. Spectrum sensing encompasses a collection of procedures intending to determine the occupancy state of a particular frequency band which is of great importance for CR. From the bandwidth of the spectrum of interesting, sensing techniques can be classified into two categories: narrowband and wideband. Usually, there are three popular sensing techniques: energy detection [2, 3], cyclostationary feature detection [4, 5], and compressed sensing [6, 7]. Energy or cyclostationary detection is based on a set of observations sampled by ADC (analog-to-digital converter) at Nyquist rate in the band of interest. Different from narrowband spectrum sensing, wideband spectrum sensing aims to find more spectral opportunities over a wide frequency range and achieve higher opportunistic aggregate throughput in cognitive radio networks. However, conventional wideband spectrum sensing techniques based on standard analog-to digital converters(ADCs) could lead to unaffordably high sampling rate or implementation complexity, thus revolutionary wideband spectrum sensing techniques become increasingly important. Due to hardware limitations on the sampling speed, these sensing techniques are primarily used to sense one band at a time. To sense multiple frequency bands, CR users may need to scan the spectrum or use multiple RF frontends for sensing multiple bands. However, using these approaches for wideband sensing either causes long sensing delay or incurs higher computational complexity and hardware cost. Compressed sensing (CS) is a new type of sampling theory, which predicts that sparse signals can be reconstructed from what is previously believed to be incomplete information. Report says that localized temporal and geographic spectrum utilization is extremely low [8], which means CS is a promising candidate to realize wideband spectrum sensing. Recent studies on compressed sensing have led to a significant amount of work on wideband spectrum sensing based on sub-Nyquist sampling [9-14]. These work focus on exactly reconstructing the primary signal. However, the assumptions in most of the work need to be relaxed for building a practical sensing algorithm. According to the sparseness of the wideband spectrum, sub-Nyquist sampling can be introduced to extend these methods. What’s more, CS is a transformation which mapping the signal from one space to another space, and the basis functions for transformation are critical for finding all the PUs’ spectrum while putting these methods into practice.

Against this background, the novel contribution of this paper is that a CS sensing algorithm is presented to sense wideband spectrum. Considering the translation invariance requirement for sensing spectrum, Gabor wavelet is introduced to construct the atoms dictionary which is the basis for signal transformation, and matching pursuit theory is used to exploiting the optimal atoms for signal representation.

The rest of the paper is organized as follows. Section 2 introduces the system model. Section 3 proposes a wideband spectrum sensing algorithm based on matching pursuit theory. Simulation results are presented in Section 4, and conclusions are given in Section 5.

2. System Model

Suppose that CRs aim to exploit spectral holes within frequency band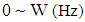. The received signal at the CRs is first down-converted to baseband before further signal processing and decision making. Without loss of generality, we consider only the equivalent baseband received signals 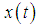throughout the paper. The process of cooperative sensing starts with spectrum sensing performed individually at each CR user called local sensing. Typically, local sensing for primary signal detection can be formulated as a binary hypothesis problem as follows [15]:

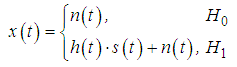(1)

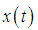where is the equivalent baseband signal received by secondary user during the sensing period, 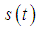is the signal from the primary user, 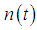is stochastic noise, and 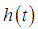is the temporary amplitude gain of the channel. 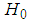and 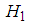denote as the hypotheses of the absence and the presence of the primary user. By using sampling rate 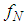over the observation time τ, we could obtain a discrete time sequence 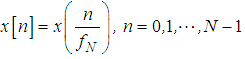, in a vector form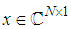. Here, 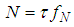is chosen to be a natural number.

Document [8] reports that localized temporal and geographic spectrum utilization are extremely low. What’s more, compressive theory indicates that, if a signal is sparse in some basis, it can be reconstructed by using signal sampled with a sub-Nyquist sampling rate. Mathematically, by using sub-Nyquist sampling rate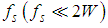, the compressed samples 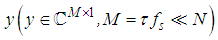can be written as

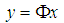(2)

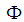where denotes an 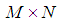measurement matrix. For spectrum sensing system, the goal is to reconstruct 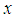or its discrete Fourier transform (DFT) spectrum 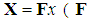denotes a DFT matrix ) from 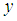[16].

3. Wideband Spectrum Sensing Algorithm Based on Matching Pursuit

3.1. Compressed Sampling

Let 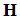be a Hilbert space, we define a dictionary as a family 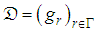of vectors in 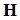, such that 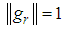, 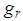are called time-frequency atoms. Depending upon the choice of time-frequency atoms, the decomposition might have very different properties.

Let 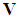be the closed linear span of the dictionary vectors. Finite linear expansions of vectors in 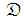are dense in the space 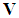. We say that the dictionary is complete if and only if 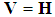. When the signal space 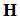has a finite dimension 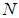, the dictionary 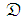may have an infinite number of elements and it is supposed to be complete. Document [17] gives an efficient implementation of matching pursuit algorithm and prove that the norm of residues decays exponentially, which is very important for sparse representation.

Suppose 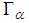is a finite index set included in 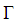such that for any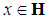

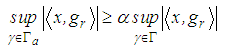(3)

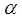Depending upon and the dictionary redundancy, set 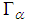can be much smaller than 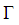. The matching pursuit is initialized by computing the inner products 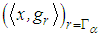. Let 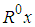be the residual vector after approximating 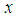in the direction of 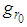, the vector 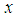can be decomposed into

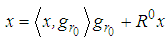(4)

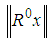To minimize , such 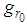is chosen that 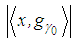is maximum

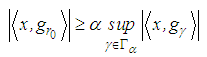(5)

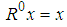Let , and the 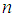th order residue 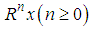is sub decomposed into

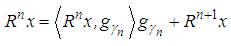(6)

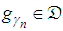where , which closely matches the residue 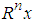. After 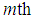iteration, the original signal can be represented as

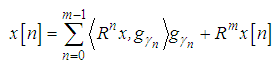(7)

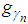Once the vector is selected, we compute the inner product of the new residue 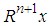with any 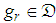, and an updating formula can be derived

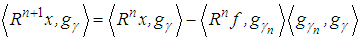(8)

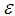The number of sub-decomposing times depends on the desired precision . The number of iterations is the minimum 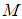such that

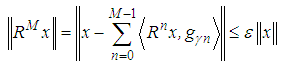(9)

which is equivalent to

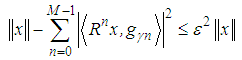(10)

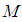The number depends upon the decay rate of 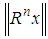, and it is much smaller that N in most applications. There exists

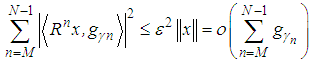and 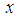can be represented as

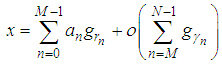(11)

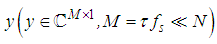The compressed samples can be written as

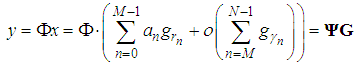(12)

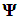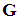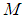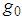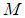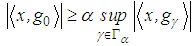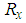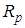where is an observing matrix, and is a matrix constructed by optimal atoms. Assume and corresponding to the atoms and the indices that maximum , respectively, and corresponding to the residual and the projection of the signal. 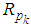is the kth 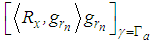, 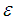is the desired precision, and 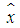is the approximation of 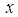. The main steps of compressed sampling algorithm are summarized below.

3.2. Wideband Spectrum Reconstruction

The next step is to reconstruct wideband spectrum. First, the Wigner distribution of signal 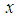is introduced, which is defined as

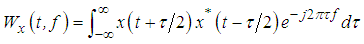(13)

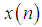For a discrete signal , defined over 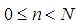, the integral is replaced by a discrete sum

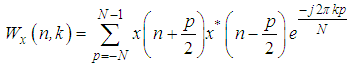(14)

The Wigner distribution of (14) is quadratic. Based on (11) and (14), we can get

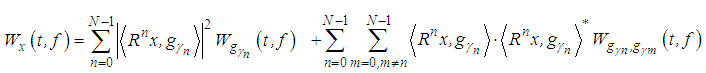(15)

The later item of (15) corresponds to the cross terms of the Wigner distribution. It regroups the terms that one usually tries to remove. The spectrum energy can be reconstructed by using

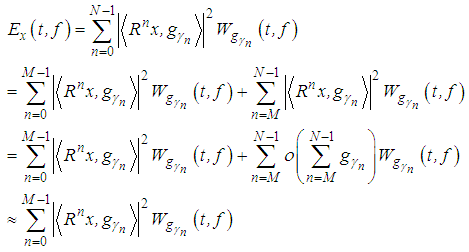(16)

3.3. Construction of Atom Dictionary

Now the key issue is how to select atoms and how to construct dictionaries with these atoms adapted to signal properties. To analyze signal structures of different sizes, it is necessary to use time-frequency atoms with different time supports. A time-frequency atom dictionary is complete, and a general family of time-frequency atoms can be generated by scaling. Wavelet is a good choice for time-frequency atoms because it can reveal many signal properties and it can lead to a fast computational algorithm. A wavelet is a function 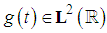with a zero average

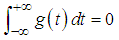(17)

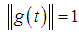It is normalized and centered in the neighborhood of 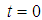. A dictionary of time-frequency atoms is obtained by scaling 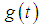by 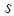and translating it by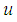

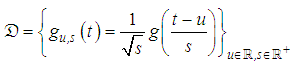(18)

These atoms remain normalized: .

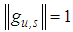Wideband spectrums are signals that have properties that rapidly change in time and frequency. The properties of a wideband spectrum are revealed by transforms that decompose signals over elementary wavelet atoms. Representing a wideband spectrum with its independent factors is a form of translation invariance that is important for spectrum sensing. Decomposition in orthonormal bases lack this translation invariance. Matching pursuits are translation invariance if calculated in translation-invariant dictionaries. An atoms dictionary 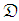is translation invariant if for any 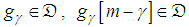for 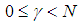. From the formula (7), it can be concluded that the matching pursuit of 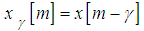selects a translation by 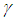of the same vectors 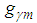with the same decomposition coefficients:

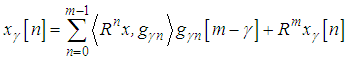(19)

Thus, spectrums identification can be characterized independently of their position. Translation invariance is generalized as an invariance with respect to any group action [17]. Wideband spectrum sensing can be viewed as a frequency translation which is an example of a group operation. If the dictionary is invariant under the action of a group, the pursuit remains invariant under the action of the same group. Among various wavelet bases, Gabor functions provide the optimal resolution in both the time and frequency energy concentration. More important, Gabor dictionary is translation invariant in time and frequency domain. Thus, Gabor wavelet transform seems to be the optimal basis to extract local features [18, 19]. Gabor wavelet has been used in many applications, such as face recognition [19, 20], texture classification [21, 22], facial expression classification and some other researches. A time and frequency translation-invariant Gabor function is constructed in [9] and [23] by scaling, modulating and translating a Gaussian window on the signal-sampling grid. 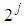For each scale , a discrete Gaussian window is defined by

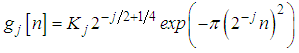(20)

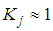where the constant is adjusted so that 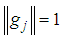. A Gabor time-frequency frame is derived with time intervals 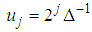and frequency intervals :

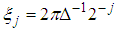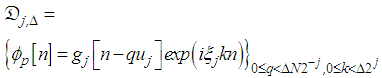(21)

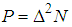It includes vectors. Theorem 5.19 in [24] proves that a necessary condition to obtain a frame is that 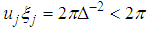, and thus 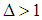. Table 5.3 in [24] shows that for 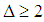, the Gabor dictionary is nearly a tight frame.

A multiscale Gabor dictionary is a union of such tight frames

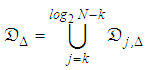(22)

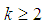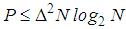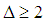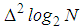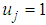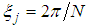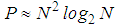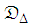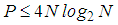with typically to avoid having too-small or too-large windows. Its size is thus , and for , it is nearly a tight frame with frame bounds . A translation-invariant dictionary is a much larger dictionary obtained by setting and in (21), and it thus includes vectors. A smaller size dictionary with for 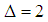is selected in this paper. The position and frequency of this atom are refined with formula (5). It finds a close time-frequency atom 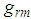in the larger translation-invariant dictionary, which has a better correlation with .

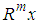4. Simulation Results

In simulation, we consider the wideband signals are subject to additive white Gaussian noise(AWGN) across channels, which is motivated in communication scenarios for several reasons [25]: First, widespread is approximately Gaussian distributed since they are generated as linear combinations of many independent (or nearly independent) subcarriers. Second, the Gaussian distribution is the distribution that achieves the capacity of an additive white Gaussian noise channel. Third, it is a working assumption very common in signal processing and statistics since it leads to tractable models and since many methods designed for Gaussian distributions also work even when there exist considerable departure from Gaussianity. The wideband signal used in this paper has the same style as the signal in [16]

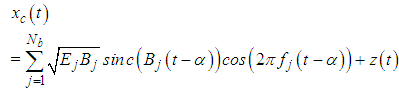where , 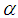is a random time offset, 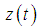is AWGN with zero mean and unit variance, 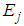is the receive power at CR. The overall bandwidth 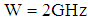. The signal-to-noise ratios (SNRs) are natural numbers between 7dB and 27 dB.

The integer undersampling scheme in [26] is used to sample the entire bandwidth all at once, in which the sampling rate is an integer fraction of the wideband Nyquist rate. And the relationship between the frequency samples 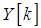for integer undersampling and the frequency samples 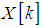for wideband Nyquist sampling is [26]

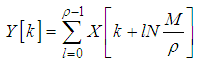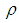where is the sub-sampling factor, which is defined as the ratio of the Nyquist rate to the actual sampling rate, 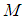is the number of narrow-band frequency channels. Each channel has equal bandwidth 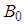and the entire wideband width is 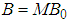. 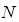is the number of wideband Nyquist samples per channel in a sensing window. Thus the entire sensing window duration for wideband Nyquist sampling is 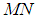samples. 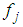is the central frequency of the jth PU signal, 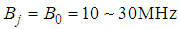. The spectrum sensing length is 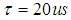. Rather than using the Nyquist sampling rate 4GHz, 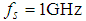is adopted. The total samples are 20000. According to the construction of the Gabor atoms in formula (21), the parameters of the Gabor atom are set as: , , ,

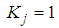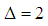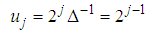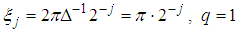According to the analysis in Section 3, the atoms number in a dictionary is 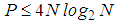for 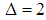, here N is the dimension of the vectors. In this simulation, the maximum atom number is set to 8.

The simulation results in Fig.1 show the PU’s reconstruction when 8 times are run to select the optimal atoms. Fig.1(a) is the original signal of wideband and Fig.1(c) is the reconstructed signal using Gabor atoms based on compressive sensing, which shows that the PU’s spectrum can be reconstructed correctly. Fig.1(b) is the relationship between selected atom index and the run sequence. Fig.2 illustrates the coefficients of the selected atoms and the atom index, which shows that most of the coefficients are zero. Thus, the coefficients vector is sparse, and we should only save those nonzero coefficients and their indexes, which can decrease the memory cost greatly. Fig.3 shows the relationship between the normalized reconstructed error and the number of selected atoms, which illustrated that normalized reconstructed error is fluctuant and the local minimum error can be obtained when 2 atoms are selected.

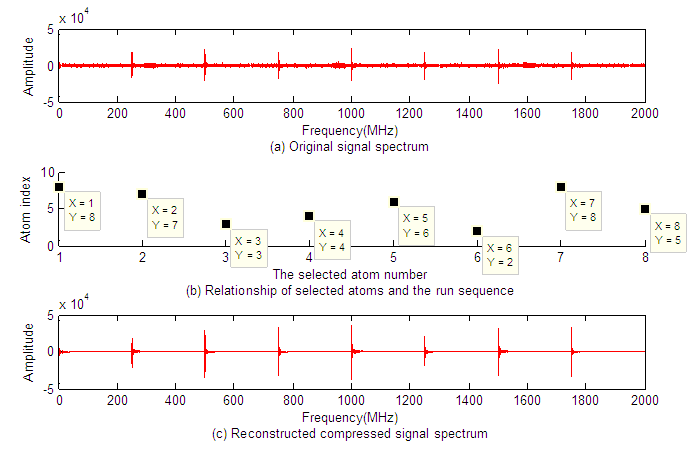Figure 1. Simulation Results of Wideband Spectrum Sensing Algorithm

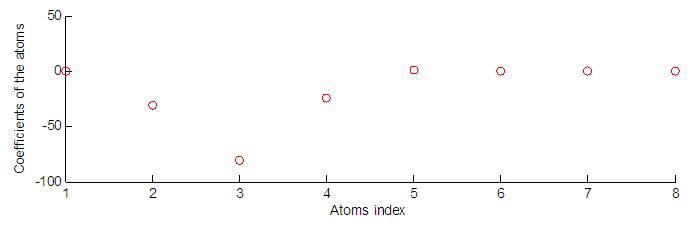Figure 2. Coefficients of the selected atoms

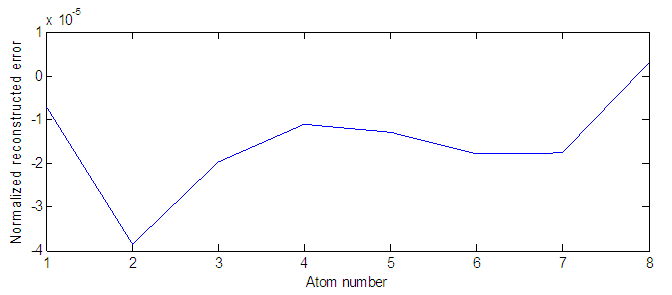Figure 3. Reconstruction error with the number of atoms

Compared with [16], the method presented remains the high throughput gain for its sampling scheme. The minimum recovery error in [16] is close to 10^-2 when system parameter meets some requirement. However, the recovery error of the method in this paper is much lower than that in [16]. What’s more, the atoms coefficients are sparse, which infers that the sampling rate can be decreased further if needed, and this can be used to settle the bottleneck of ADC.

5. Conclusions

The challenges in the spectrum sensing for wideband are presented. Then based on the fact that wideband spectrum sensing is critical for reliably finding spectral opportunities and achieving opportunistic spectrum access for next generation networks, a compressed sensing method is presented to solve the unaffordable sampling rate for wideband spectrum sensing. Finally, a computer simulation is done to verify the feasibility of the wideband spectrum sensing method, which shows that the method presented can greatly decrease the dimension of the signal under sub-Nyquist sampling theory.

ACKNOWLEDGEMENTS

The work is partially supported by the National Natural Science Foundation of China (No.61102035 and No. 61201108), the Fundamental Research Funds for the Central Universities, China Postdoctoral Science Foundation (2014M551798), Chunhua Foundation of Hefei University of Technology (2014HGCH0012), Excellent Talents in Hunan Normal University (2012).