1. Introduction

Fibre and textile reinforced composite structures are typically characterised by outstanding specific strength and stiffness properties. Moreover, the composite-specific high design flexibility of the anisotropic mechanical properties enables construction of high speed rotors with considerable performance enhancement compared to rotors made of conventional materials[1]. Nevertheless, to ensure safe, economical and efficient operation of high speed rotating machinery equipped with such rotors, an implementation of reliable and cost-effective damage detection methods is still necessary[2].

Currently developed Structural Health Monitoring (SHM) techniques for composite structures are mostly focused on detection of fatigue or impact-caused structural faults of non-rotating components[3-7]. Most of these techniques are based on the analysis of vibration signals obtained using either the external or structure-embedded sensors.

Since any damage initiation in the rotor causes changes in the dynamic behaviour of the whole machine (Fig. 1), the damage-detection procedures typically consider changes of modal parameters, i.e. natural frequencies, mode shapes, and modal dampings[8-10].

Systems which enable monitoring of rotating structures made of conventional materials have been already reported and validated[11-13]. However, application of such systems to high-speed composite rotors is very challenging due to numerous dynamic rotation-related dynamic phenomena like crack-breathing, dynamical mechanical stress redistribution or tension-bending coupling emerging due to damage. Some metrological problems while using embedded sensors resulting from the influence of centrifugal forces on readout accuracy as well as the transmission of measured signals to a stationary analyser need to be considered as well[14].

A key issue in designing on-line SHM systems is the identification of the unequivocal diagnostic relations between features of measurable physical signals generated by the machine such as noise or vibration and the existing damage condition. Identification of the diagnostic relations requires from one side an application of appropriate and sufficiently accurate measurement systems and from other side signal processing and analysis methods which enable the determination of sensitive signal features.

This paper presents numerical and experimental investigations of the influence of delamination on dynamic behaviour of composite disc rotors. Vibration modes described by modal parameters such as natural frequencies and mode shapes were considered as diagnostic features enabling the assessment of the structural condition. In order to identify the sensitivity of particular vibration modes to delaminations of different size and position, a finite element (FE) model was created and series of simulations were conducted. For the calibration and validation of the FE model, an off-line experimental modal analysis was conducted on several composite disc rotors.

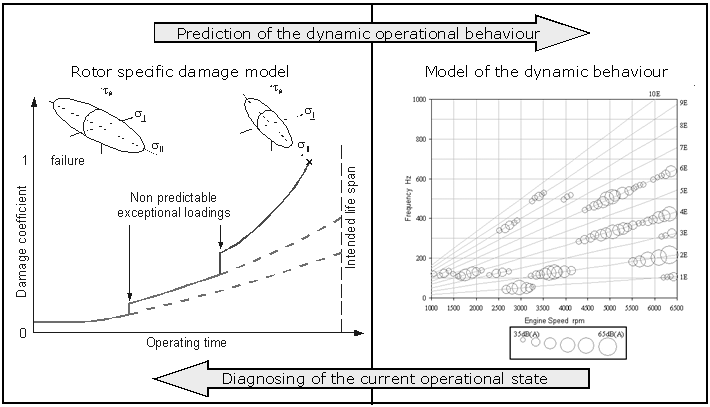Figure 1. Influence of material damage evolution on the rotor dynamic behaviour

2. Investigation Procedure

The damage presence in a composite structure causes, among others, a reduction of its dynamic stiffness resulting in alteration of natural frequencies and mode shapes[6]. Thus, the observation of these parameters of the structure during its operation offers the possibility of detecting the damage occurrence and its evaluation.

The aim of the research was mainly to identify qualitative relations between through-thickness positions of delamination and modal parameters of composite disc rotors. This information can be useful for a further development of diagnostic methods for rotating composite structures.

The proposed procedure involves the following steps:

• manufacturing of composite disc rotors with and without introduced delamination,

• experimental modal analysis of produced disc rotors,

• design of a parametrised FE model of delaminated disc and its validation using experimentally obtained modal parameters,

• conduction of numerical modal analysis for numerous configurations of delamination,

• determination of regularities in numerical and experimental results caused by delamination.

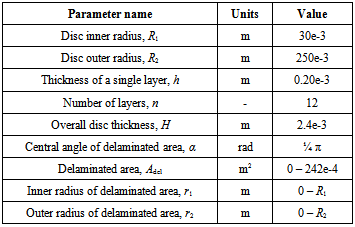
3. Investigated Object

The analysed object was a multilayered composite disc made of 12 glass fibre reinforced epoxy resin layers with and without introduced delamination. The stacking sequence of the disc was[0 / 60 / -60 / -60 / 60 / 0]_S. Such arrangement of reinforcing fibres results in quasi isotropic in-plane properties of the structure.

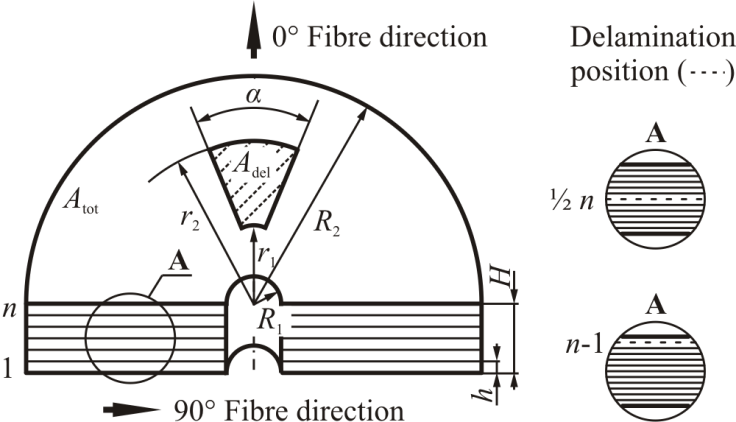Figure 2. General view of the investigated rotor and examples of the trough thickness delamination position

Table 1. Geometrical parameters of the investigated delaminated disc

Table 2. Cases considered for the calibration and validation of the FE model

In the study, different combinations of area and through-thickness position of delaminations were considered. The experimental cases used for calibration and validation of the FE model are summarised in Tab. 2. Here, four rotors with delamination area located between the middle plies no. 6 and 7 (denoted as ½ n) and between the surface plies no 11 and 12 (denoted as n-1) were considered. Additionally, rotors without any damage were examined in order to:

• obtain the reference modal parameters, and

• asses the scatter of modal parameters due to manufacturing process tolerances.

The disc rotors were manufactured from laminated glass fibre reinforced epoxy. Firstly, several rectangular plates were produced using the autoclave prepreg technique. During the production process pieces of polytetrafluoroethylene (PTFE) film were inserted between the plies of selected plates. The PTFE is characterised by a very low friction coefficient – µ_s ≈ 0.04 – and hence is suitable to simulate the effect of delamination as a lack of bonding between the plies.

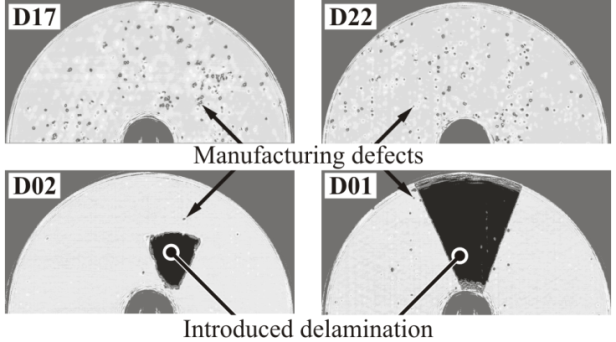Figure 3. Examples of ultrasonic scan images of manufactured discs

The disc rotors were cut out of the consolidated plates using water-jet technique and subsequently scanned with the use of the ultrasonic transmission (shadow) technique to find the material’s non-homogeneities which are usually caused by the manufacturing defects, e. g. air bubbles or cavities induced during the production process. Additionally, the scans allowed a classification of the discs into subsets with similar number and distribution of aforementioned technological defects. Examples of ultrasonic scans of reference (defect free) and delaminated discs are shown in Fig 3.

4. Experimental Modal Analysis

The aim of the experimental work was to determine the modal parameters of manufactured healthy and damaged rotors. This information provides the basis for the verification of the developed numerical model.

4.1. Experimental Set-up

Experimental modal analysis was conducted using modal hammer as force exciter, and Laser Doppler vibrometer as vibration sensor. Such configuration of experimental set-up enables the determination of modal parameters with a minimal influence of transducers’ mass and simultaneously assures high measurement accuracy.

The disc rotors were clamped in the centre with the use of a stiff clamping system. Every disc was excited with an impulse force signal in one fixed point (v. Fig. 4) using the modal hammer. The modal hammer was fixed to a revolute joint with a swing end stop mechanism in order to assure repeatable excitation force characteristics. The structural response was measured with the help of a single point Laser Doppler vibrometer in 32 regularly distributed measuring points as shown in Fig. 4.

The force and velocity signals recorded using a triggered signal analyser were used to determine the frequency response function (FRF) in form of mobility calculated as velocity/force.

The measurements were performed in the frequency range from 0 to 400 Hz with a frequency resolution of 0.25 Hz. An exponential window in the time domain was applied to the excitation and the response data and each FRF was averaged in the frequency domain from 5 independent impact events. In order to estimate modal parameters, a frequency domain algorithm based on orthogonal polynominal curve fitting method was used. Modal parameters were extracted for each disc using the modal analysis software[15] from a set of 32 measured FRFs.

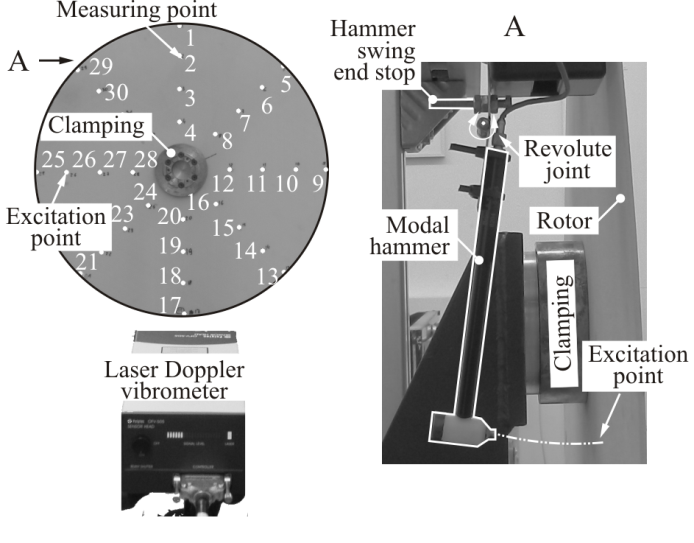Figure 4. The configuration of experimental set-up for the determination of modal parameters with marked measuring and excitation points

4.2. Results

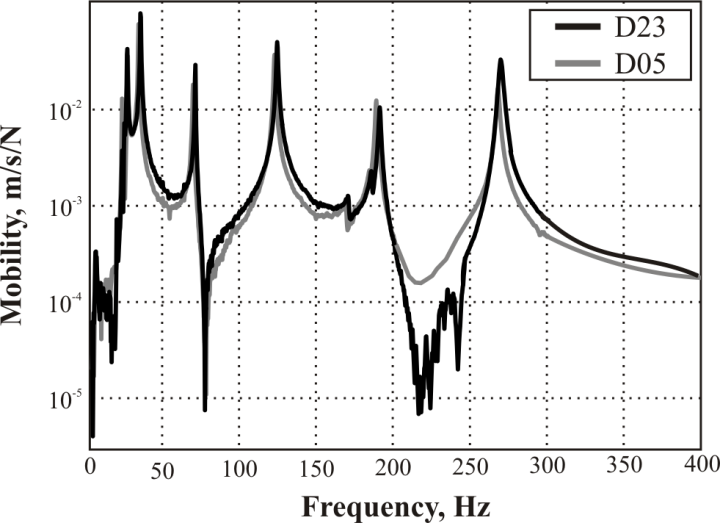Figure 5. Example of FRFs obtained for discs without and with delamination of 3% located on ply (n-1) for measuring point 1 (cp. Fig. 4)

Exemplary plot of FRFs obtained for disc without (black line) and with 3% delamination (gray line) is presented in Fig. 5. Based on the experimentally obtained FRFs, the first 13 eigenfrequencies were identified for all considered discs. Since the investigated rotors are generally symmetric structures, double modes can be observed. Considering that such modes are weakly separated, not all expected modes could be unquestionably identified from the FRFs. In such cases an assumption was made that the eigenfrequency is the same for double modes.

The first five eigenmodes of a healthy rotor are presented in Fig. 6.

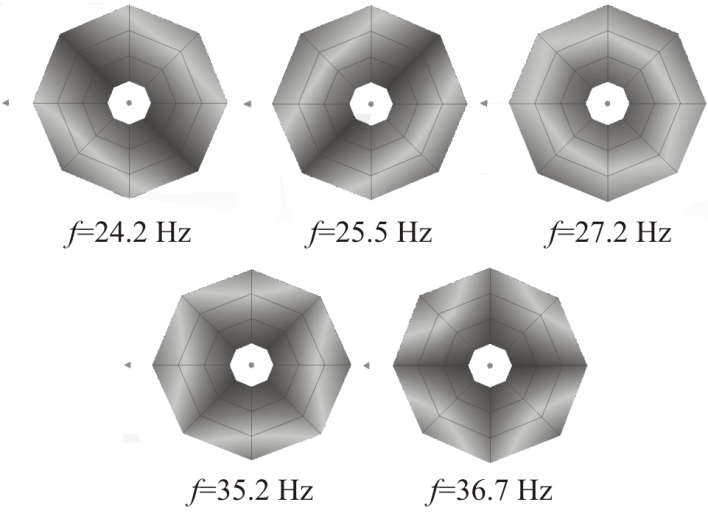Figure 6. Eigenmodes of the D17 healthy rotor. The eigenfrequencies are the mean values of all healthy rotors

The obtained FRFs for every rotor indicate a clear dependency of modal parameters from the delamination. However, the fact that every rotor was slightly different could result in erroneous estimation of delamination-caused changes in the modal parameters. Hence, the influence of manufacturing scatter as well as the sensitivity of eigenfrequencies to delaminations was analysed.

4.3. Sensitivity Analysis of Modal Parameters to Manufacturing Scatter and Delaminations

In the sensitivity analysis, firstly modal parameters scatter due to manufacturing tolerances and repeatability of measurement system were estimated for the healthy rotors. The scatter of eigenfrequencies between three undamaged rotors was calculated. The minimal, maximal as well as the mean value of eigenfrequency are presented in Fig. 7 in black colour bars. The change of eigenfrequency due to introduced delamination is presented with gray markers on the same figure.

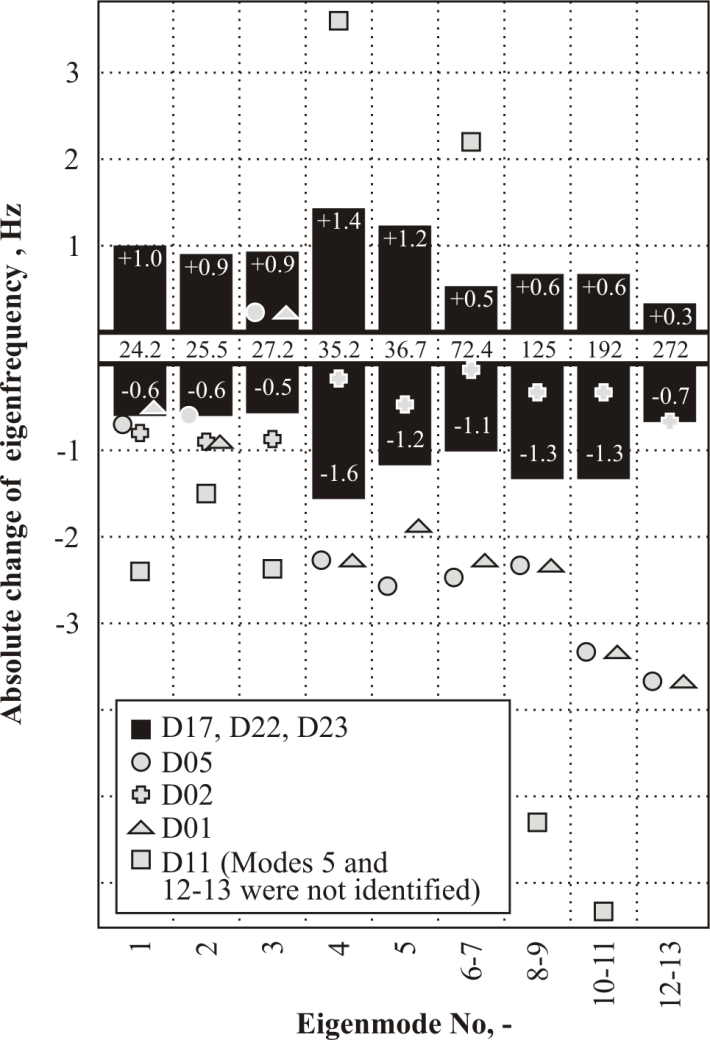Figure 7. Sensitivity of particular eigenmodes to induced delamination

Analysis of the variations presented in Fig. 7 enables the following conclusions:

• the change of the eigenfrequencies as effect of introduced delamination is clearly observable despite the manufacturing tolerances,

• low eigenfrequencies with simple eigenforms (cf. Fig 6) perform less sensitive than higher frequencies,

• the increase of the delamination size (pairs D02-D01 and D05-D11) change the eigenfrequency generally monotonically – the bigger delamination area the higher change of eigenfrequency,

• the through-thickness position of the delamination (pairs D05-D02 and D01-D11) could be initially estimated as follows: the closer to neutral laminate axis the higher change of eigenfrequency.

5. Numerical Modal Analysis

Since the amount of available experimental data was not sufficiently large for the formulation of generalised relations, an FE model was developed and calibrated using the experimentally obtained modal parameters. The numerical modal analysis was then performed in order to generate data for different cases of delamination and to formulate extended qualitative relations between delamination characteristics and modal parameters.

5.1. Parametrised FE Model of the Disc Rotor

The disc rotor was modelled with the use of commercially available finite element software[16]. Element SOLSH190 was used to model behaviour of an individual layer of the composite rotor and element CONTAC52 was used to model the delamination. The principle of connecting finite element SOLSH190 with CONTAC52 is presented in Fig. 8. The application of CONTAC52 allows the modelling the behaviour of delaminated layers by preventing their penetration. The remaining degrees of freedom in the delaminated region are allowed.

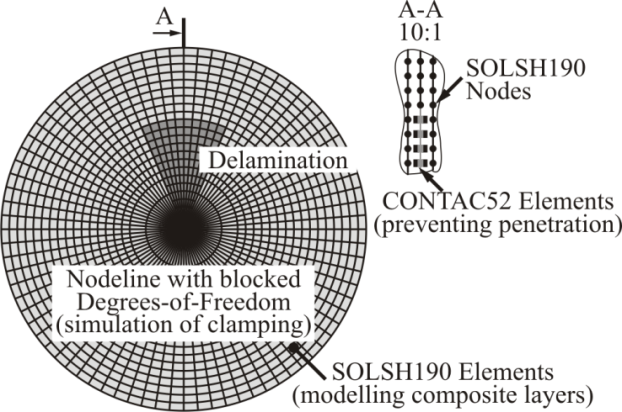Figure 8. General overview on the developed parametrised FE model

Properties of composite material used in FE models were obtained experimentally in tensile tests[17]. The tests were carried out on specimens manufactured from 8 layers of uni-directional composite plate made of prepreg tapes, identical with those used for the manufacturing of disc rotors. The obtained results are summarised in Tab. 3.

Table 3. Mechanical material properties used as initial values in modelling process

5.2. Model Calibration

An important prerequisite for the successful application of the created FE model lies in its proper calibration. Here, the experimentally obtained material parameters were varied within a narrow range in order to match the simulated modal parameters with those obtained in the experiments. Such procedure is inevitability required to include effects of unknown magnitude like limited stiffness of the clamping, manufacturing scatter, and problematic measurement of shear modulus.

A comparison of eigenfrequencies simulated using calibrated FE model and those obtained experimentally is presented in Fig. 9. A summary of the optimised model parameters is presented in the Tab. 4.

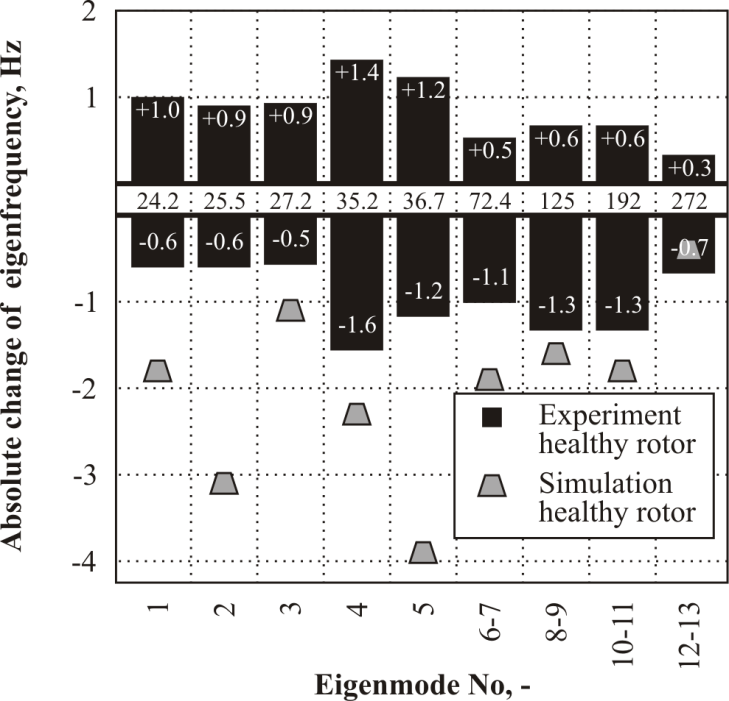Figure 9. Goodness-off-Fit of modal parameter simulation after FE model calibration for undamaged rotor

The Goodness-of-Fit presented on Fig. 9 indicates that the developed model do not cover all phenomena observed during the experiments. For example – in contrast to real rotors – double modes identified numerically have identical frequency what results from perfect symmetry which is not achievable in the case of real structures due to limited manufacturing precision. The local manufacturing defects, as presented in Fig. 3 (D17, D22), were not simulated. Incorporation of all aforementioned – and specific for every specimen – features into the model would impair the universality of the later formulated relations between delamination and modal parameters.

Table 4. Mechanical material properties after calibration

Using the calibrated model properties, simulations of rotors with delaminations were performed. As reference, the experimentally determined modal parameters were used. This preliminary simulation step was conducted in order to assess the quality of the proposed delamination modelling technique. The results of this investigation are summarised in the following figures.

The modal parameters obtained using the calibrated FE model in relation to those experimentally determined are qualitatively in good agreement. Merely the results for the rotor with 13% of delamination in through-thickness position ½ n exhibit higher differences. These differences could be a result of higher than in other rotors effect of residual stress release resulting in a persisting deformation changing significantly the rotor’s geometry. The maximal deviation from a perfectly horizontal flat surface of rotor D11 equals 5 mm whereas for all other rotors this value is close to zero. Since the accuracy of simulation in all cases except rotor D11 was relatively high an assumption was made that the model reproduces the considered phenomena in that cases well enough.

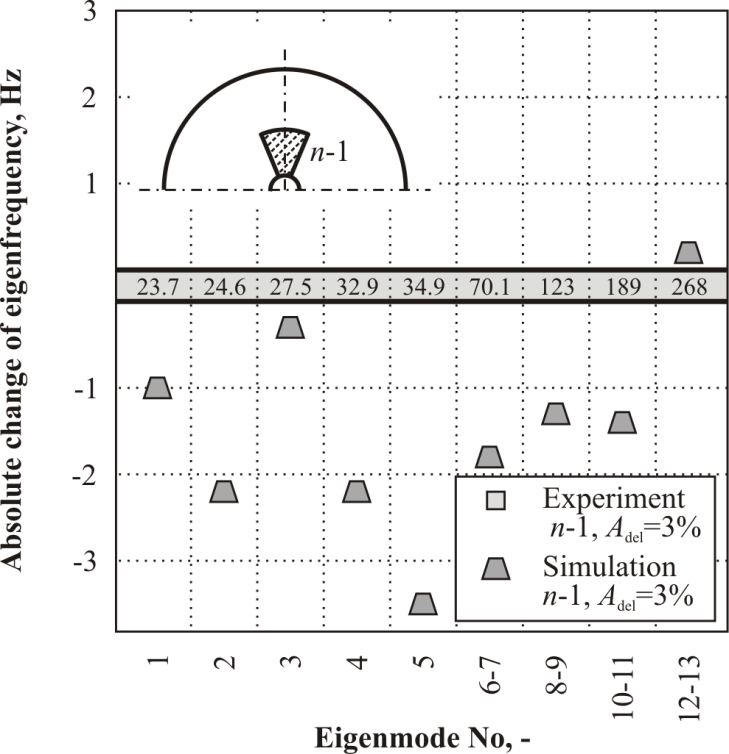Figure 10. Goodness-of-Fit for the 3% delaminated in n-1 layer rotor

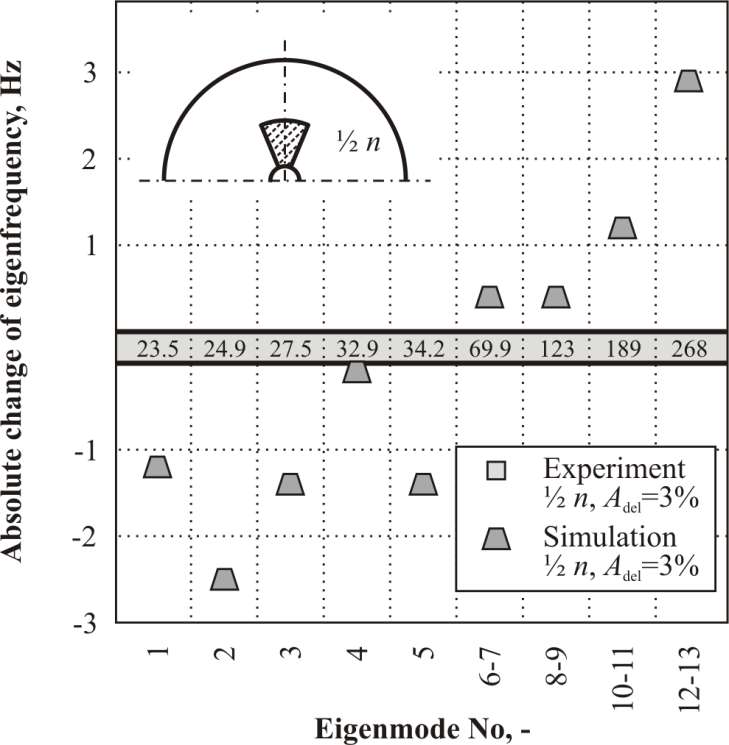Figure 11. Goodness-of-Fit for the 3% delaminated in ½ n layer rotor

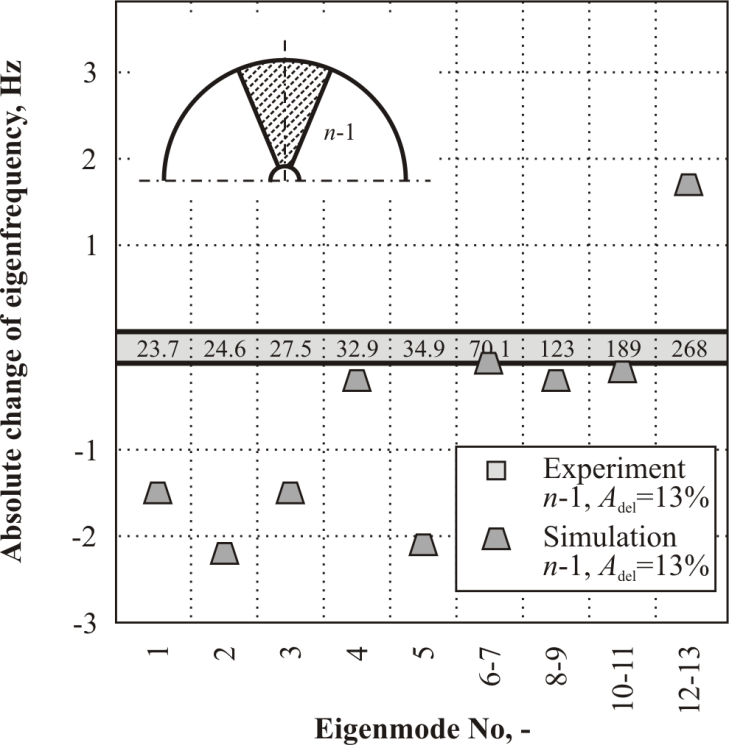Figure 12. Goodness-of-Fit for the 13% delaminated in n-1 layer rotor

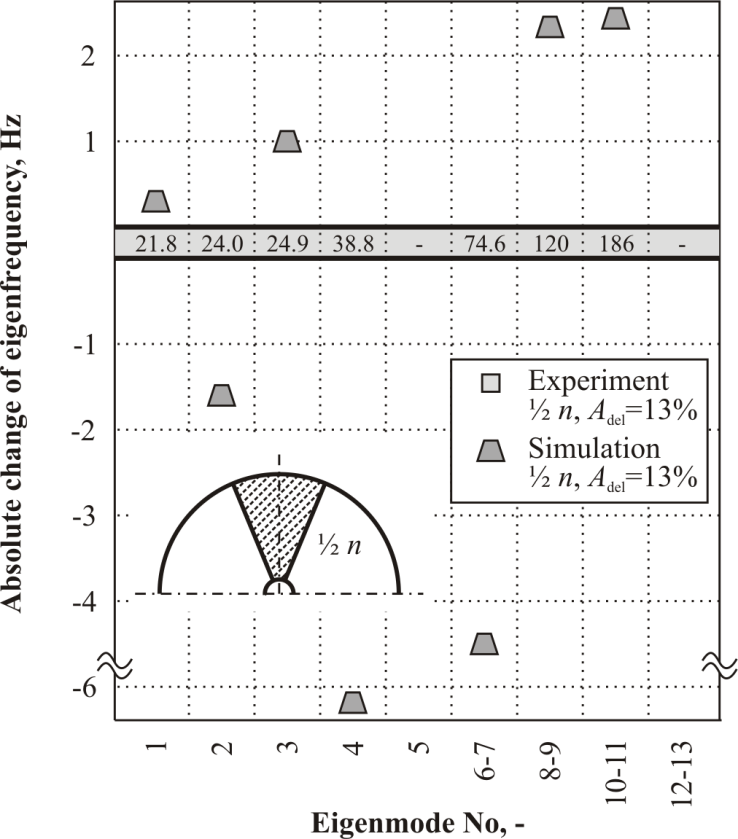Figure 13. Goodness-of-Fit for the 3% delaminated in ½ n layer rotor

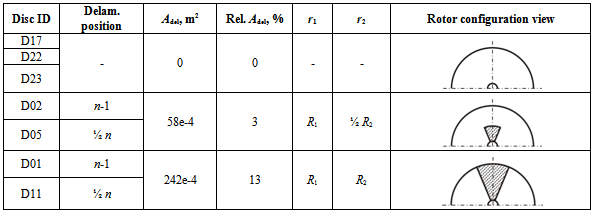
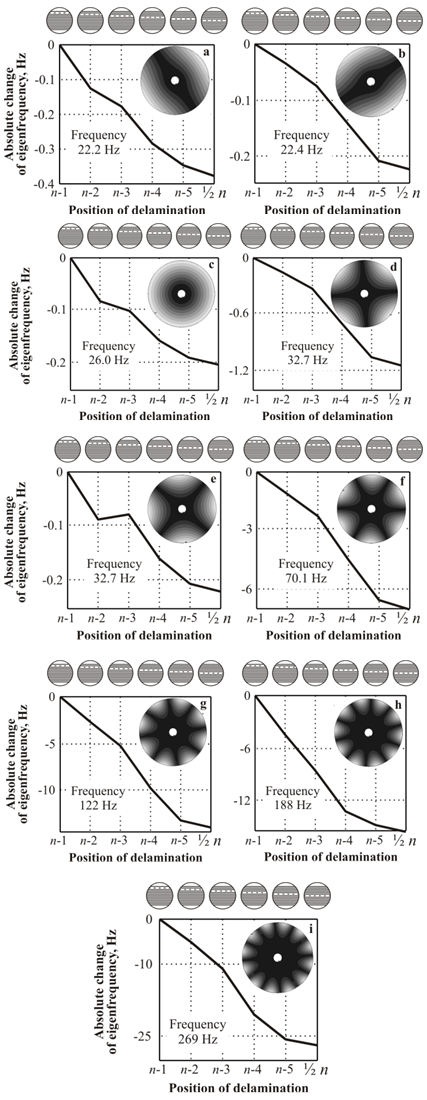
5.3. Simulation Results and Discussion

The numerical modal analysis was carried out using the calibrated parametrised FE model in order to comprehensively investigate the influence of the through-thickness delamination position on the eigenfrequencies.

This position was varied from n-1 to ½ n (assumed symetrical from top to middle ply and from bottom to middle ply). The relative size was assumed constant A_del=3%, the inner and outer delamination radius was equal r₁=R₁ and r₂=½ R₂. Results of these investigations are presented below.

Figure 14. Absolute change of the eigenfrequency due to through-thickness position variation of the eigenmodes (undamaged rotors as the reference). (a) to (f) Eigenmodes 1 to 6. (g) Eigenmode 8. (h) Eigenmode 10. (i) Eigenmode 12

The obtained results indicate a clear relation between the position of delamination and its impact on the eigenfrequencies. Generally, the shift of eigenfrequency was the greatest when the delamination’s through-thickness position was between the middle plies. The observed tendency clearly confirms the conclusions formulated based on the experimental results.

The fact of eigenfrequency reduction can be explained by the relative gliding motion of the plies adjoining the delamination (v. Fig. 15). Since no shear stress can be transmitted between those plies, the resulting bending stiffness decreases. The resulting change of bending stiffness unavoidably causes alteration of eigenfrequency[18].

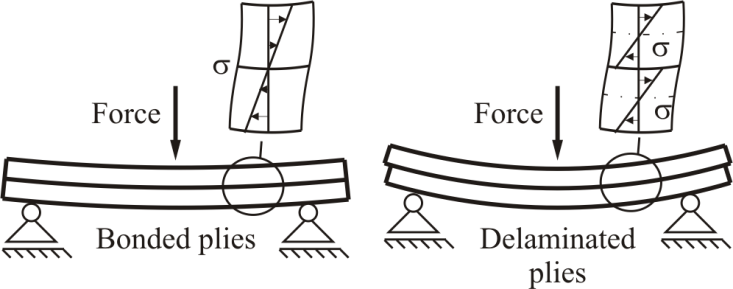Figure 15. Influence of delamination on through-thickness distribution of mechanical stress

The relation between through-thickness position of delamination and bending stiffness can be presented as follows (assuming an isotropic Young’s modulus).

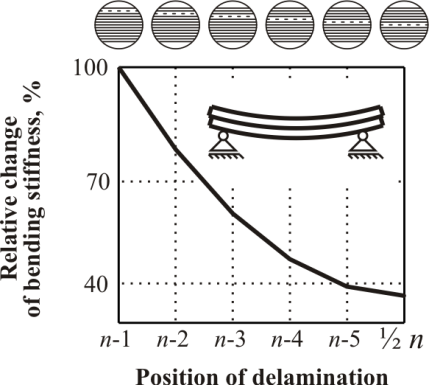Figure 16. Absolute change of bending stiffness in relation to through-thickness delamination position (Bonded ply beam as reference)

A clear relationship between the complexity of the mode shape and relative change of eigenfrequency could be observed (Fig. 14). In a thought experiment, the higher mode shapes could be approximated as a short beam under bending load. Through a shorter wavelength, the shear stress of the beam becomes more and more crucial to the beam’s behaviour. Hence, in higher modes the effect of delamination becomes more apparent.

Besides this effect, a double mode splitting was noticeable. Additionally, some local modes could be observed by higher excitation frequencies (v. Fig. 17). Detection of such phenomena could additionally improve reliability of damage detection. The latter can be only experimentally detected when a sensor (embedded, applied or external) is placed in immediate vicinity of the delamination.

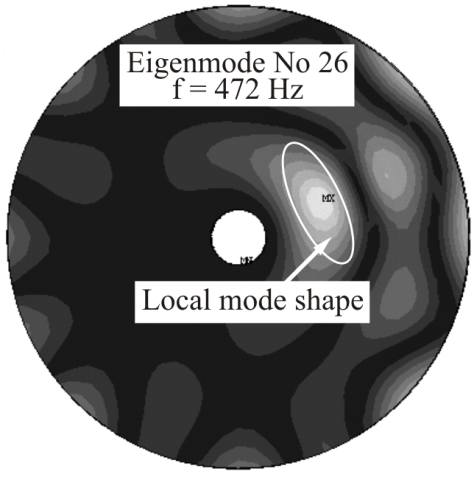Figure 17. Local mode shape as a result of delamination

6. Conclusions

The effect of delamination’s through-thickness position on the eigenfrequencies of laminated composite disc rotors has been investigated. In experimental studies healthy and delaminated rotors were considered. The results were mainly used to the numerical model calibration and validation although several regularities in the eigenfrequency change due to delamination were found.

In the numerical modal analysis, conducted using calibrated FE model, extended investigations regarding the impact of through-thickness delamination position on eigenfrequencies were performed. Obtained results of research indicate that the reduction of eigenfrequency can result from change of bending stiffness of delaminated structure.

The future work will deal with the influence of centrifugal forces on the dynamic behaviour of delaminated rotors. An appropriate experimental setup and extended simulation techniques should give an insight into complex, damage dependent patterns of modal properties at different rotational speeds.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the financial support of the European Centre for Emerging Materials and Processes Dresden (ECEMP) funded by the European Union and the Free State of Saxony.