-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2013; 3(6B): 40-52
doi:10.5923/s.cmaterials.201310.05
Effect of Core and Face Sheet Anisotropy on the Natural Frequencies of Sandwich Shells with Composite Faces
Jörg Hohe
Fraunhofer-Institut für Werkstoffmechanik IWM, 79108 Freiburg, Germany
Correspondence to: Jörg Hohe , Fraunhofer-Institut für Werkstoffmechanik IWM, 79108 Freiburg, Germany.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The objective of the present study is the analysis of the effect of core and face sheet anisotropy on the natural frequencies of plane and doubly curved sandwich structures with laminated composite face sheets and an anisotropic core. For the analysis, a higher-order sandwich shell theory is adopted. For the special case of a sandwich shell with rectangular projection, an analytical solution is obtained by means of an extended Galerkin procedure. Assuming a harmonic time-dependent response, the problem is transformed into an eigenvalue problem, which can be solved in a numerically rather efficient manner. The numerical scheme is applied to an analysis of the effect of the face sheet anisotropy induced by fibre angle variations in laminated face sheets consisting of unidirectionally infinite fibre reinforced carbon epoxy plies. Further anisotropy effects derive from the use of honeycomb cores with anisotropy transverse shear moduli. It is observed that anisotropy of core and face sheets may have distinct effects on the lower natural frequencies.
Keywords: Sandwich Structures, Composite Face Sheets, Anisotropy, Analytical Model, Natural Frequencies
Cite this paper: Jörg Hohe , Effect of Core and Face Sheet Anisotropy on the Natural Frequencies of Sandwich Shells with Composite Faces, International Journal of Composite Materials, Vol. 3 No. 6B, 2013, pp. 40-52. doi: 10.5923/s.cmaterials.201310.05.
Article Outline
1. Introduction
- Structural sandwich panels are important elements in modern lightweight structures. The typical sandwich panel is a layered structure according to Figure 1. It consists of three principal layers where two high-density face sheets are adhesively bonded to a low density core. The face sheets carry all in-plane and bending loads whereas the core keeps the face sheets at their desired distance and transmits the transverse normal and shear loads. The advantage of the sandwich principle is that plates and shells with high bending stiffness may be constructed at an extremely low specific weight (Vinson[13], Zenkert[16]).Typical face sheet materials are thin metal sheets or – especially in high performance applications – composite laminates consisting of unidirectionally infinite carbon or glass fibre reinforced plastic plies. Depending on the stacking sequence of the laminates, the face sheets may feature a distinct anisotropy which may be exploited towards the design of tailored structures with optimized properties complying with any kind of prescribed structural requirement. The core is usually made from a weak, low density material such as balsa wood, solid foam or a two-dimensional honeycomb type cellular structure. Especially honeycomb cores may feature a distinct anisotropy since their transverse shear moduli with respect to the two in-plane directions are usually not identical (Gibson and Ashby[3]).The dynamic response and vibration of sandwich structures is a challenging problem since not only the external geometry of the plate or shell but also the anisotropy of core and face sheets may affect the response of the structure. Following the pioneering experimental study by Raville and Ueng[11] in 1967, increasing interest has been directed to the vibration of sandwich plates and shells especially during the past two decades. Bardell et al.[1] have analysed the free vibration of plane isotropic sandwich plates with different external shapes using the finite element method. The free vibration of sandwich plates with laminated anisotropic face sheets has been investigated by Zhou and Li[17] as well as by Kant and Swaminathan[8] using different quasi-analytical models. Yuan and Dawe[14] employed the spline finite strip method to the analysis of the eigenmodes of plane sandwich plates with laminated composite faces. In a later study, this approach has been extended to the problem of plane sandwich plates with stiffeners on one side (Yuan and Dawe[15]). Since the deformation behaviour of sandwich structures with soft cores in general is much more complex than the response of sandwich structures with stiff, transversely incompressible cores, a number of studies use higher-order sandwich models for the analysis of the free vibration problem. Sokolinsky et al.[12] have analysed the lower natural frequencies of straight sandwich beams with isotropic core and faces using Frostig’s soft core sandwich beam model. More recently, a study on the effects of the transverse core flexibility on the vibrational response of two-dimensional sandwich plates with quasi-isotropic core and faces using an extended flexible core model has been provided by Frostig and Thomsen[2]. Meunier and Shenoi[9] have been concerned with a higher-order model accounting for damping effects whereas Nayak et al.[10] employed Reddy’s higher-order model. Both studies are concerned with plane sandwich plates. However, in contrast to the previous studies, anisotropy effects are included for both, the core and the face sheets. In a similar manner, Hause and Librescu[4] analysed the vibration of anisotropic sandwich plates based on an earlier version of the present sandwich shell theory (Hohe and Librescu[5],[6]). Again, the study is restricted to plane sandwich plates. In a preceding study by the present author (Hohe et al.[7]) on the transient response of sandwich structures during and after rapid loading, the effect of curvature has been included. Nevertheless, the study is again restricted to sandwich panels made from isotropic materials.Objective of the present contribution is an analysis of the effects of the anisotropy of core and face sheets on the lower natural frequencies of plane sandwich plates as well as cylindrical and doubly curved sandwich shells. Special interest is directed to interaction effects between the external shape and the local core and face sheet anisotropy. The analysis is based on a general model for curved sandwich shells presented earlier by the present author (Hohe and Librescu[5],[6]). The original nonlinear model is simplified and adapted to the requirements of the present linear problem. Based on an extended Galerkin procedure, an analytical displacement solution is derived. Assuming harmonic oscillations as the only relevant type of displacement, an eigenvalue problem for the natural frequencies in different eigenmodes is obtained. The problem is solved numerically by means of the Newton-Raphson method. In parametric studies the effect of core and face sheet anisotropy on the lower natural frequencies for a sandwich shell with carbon epoxy face sheets and honeycomb core is studied. It is observed that the core and face sheet anisotropy may have different effects on the different eigenfrequencies.
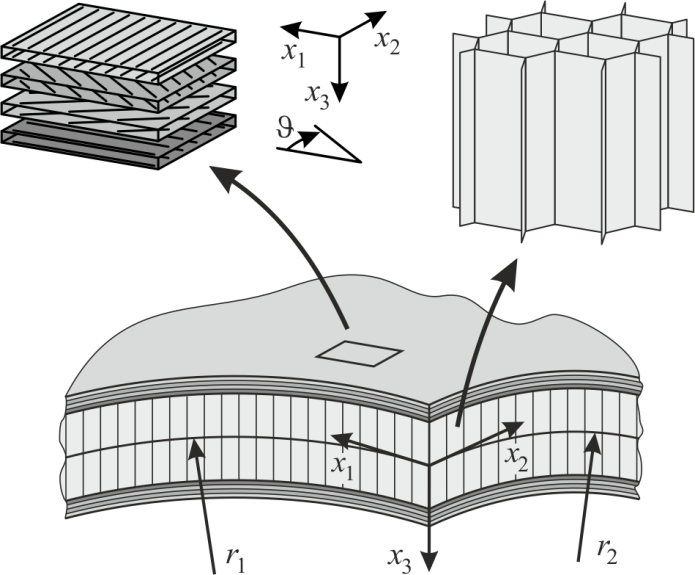 | Figure 1. Doubly Curved Sandwich Shell |
2. Sandwich Shell Model
2.1. Basic Assumptions
- For the analyses of the present study, the general shell model for shallow sandwich shells presented earlier (Hohe and Librescu[5],[6]) is adopted. The model is re-formulated into a simplified version complying with the requirements of the present problem.Consider a plane or curved sandwich shell according to Figure 1. The face sheets are assumed to consist of composite laminates with constant thickness tf. The core thickness tc is also uniform but much larger than the face sheet thickness tf. The sandwich panel is assumed to be doubly curved with radii of curvature ri which are much larger than the panel thickness so that the conditions of shallow shell theory are satisfied (Figure 1). For the analysis of the sandwich structure, a local Cartesian system xi is introduced, where x1 and x2 are the in-plane direction whereas x3 is the transverse normal direction.Both, the core and the face sheets are assumed to be linear elastic but anisotropic. For the core, the effective material parameters are assumed to be known directly whereas the face sheet material response is assumed to be given in terms of the laminate stiffness matrix of the classical laminate theory. Since the deflections in the free vibration problem in general are small, a geometrically linear analysis is sufficient. No geometric imperfections are considered, although both features are included in the original model (Hohe and Librescu[5],[6]).
2.2. Kinematic Relations
- For a projection of the shell deformation behaviour onto the reference surface, the three dimensional displacements are expanded into a power series in terms of x3. Since the material response and the thickness of core and face sheets are rather different, an effective multilayer model is adopted, treating the three principal layers (core, top and bottom face sheet) separately.Since the face sheets are thin, the Kirchhoff-Love model is adopted for the faces. Thus, the face sheet displacements are given by
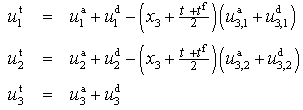 | (1) |
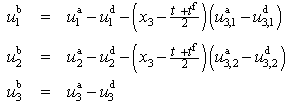 | (2) |
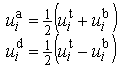 | (3) |
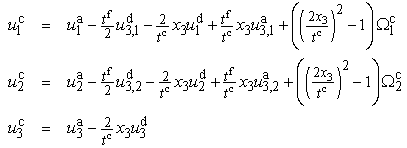 | (4) |
 are additional displacement functions. These additional degrees of freedom describe a quadratic displacement through the layer thickness in addition to the mid-surface displacements as well as the rotations and thus account for the warping of the core.From Equations (1) to (4), the strains for the three principal layers are obtained by substituting the expressions into the geometrically linear kinematic relation. Under the assumption of the shallow shell limit, the strains
are additional displacement functions. These additional degrees of freedom describe a quadratic displacement through the layer thickness in addition to the mid-surface displacements as well as the rotations and thus account for the warping of the core.From Equations (1) to (4), the strains for the three principal layers are obtained by substituting the expressions into the geometrically linear kinematic relation. Under the assumption of the shallow shell limit, the strains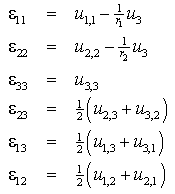 | (5) |
2.3. Equations of Motion
- In the next step, equations of motion have to be determined, which are consistent with the assumptions made in the kinematic considerations. A natural manner to determine an inherently consistent shell theory is the use of Hamilton’s variational principle
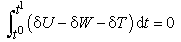 | (6) |
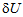 ,
, 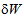 and
and 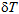 are the variations of the strain energy, the work by the external loads and the kinetic energy respectively whereas[t0, t1] is an arbitrary time increment.In the context of the present multilayer model and the corresponding simplifying assumptions, the variation of the strain energy is defined by
are the variations of the strain energy, the work by the external loads and the kinetic energy respectively whereas[t0, t1] is an arbitrary time increment.In the context of the present multilayer model and the corresponding simplifying assumptions, the variation of the strain energy is defined by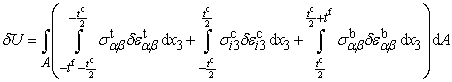 | (7) |
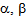 = 1, 2 whereas i, j = 1, 2, 3. The work of the in-plane stresses within the core layer is neglected.Assuming that only transverse normal distributed loads q3t* and q3b* act on the surfaces of the top and bottom face sheets, the variation of the work by the external loads read
= 1, 2 whereas i, j = 1, 2, 3. The work of the in-plane stresses within the core layer is neglected.Assuming that only transverse normal distributed loads q3t* and q3b* act on the surfaces of the top and bottom face sheets, the variation of the work by the external loads read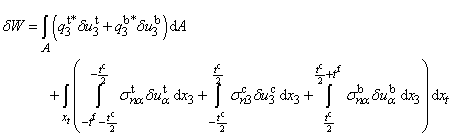 | (8) |
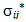 are acting.For the kinetic energy, an additional simplification is introduced by neglecting all in-plane and rotational inertia effects since in the free vibration problem, the transverse motion within the x3-direction is the dominant mode of deflection. With this assumption and the mass densities
are acting.For the kinetic energy, an additional simplification is introduced by neglecting all in-plane and rotational inertia effects since in the free vibration problem, the transverse motion within the x3-direction is the dominant mode of deflection. With this assumption and the mass densities 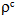 and
and 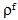 for the core and the face sheets respectively, the variation of the kinetic energy becomes
for the core and the face sheets respectively, the variation of the kinetic energy becomes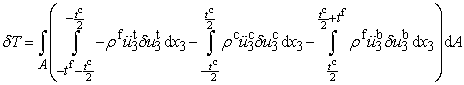 | (9) |
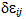 for the three principal layers of the sandwich structure using Equation (5) and substituting the result together with the shell kinematics (1) to (4) into Hamilton’s principle (6) with the variations of the strain energy, work by the external loads and kinetic energy according to Equations (7) to (9) results in a lengthy variational expression. Within this expression, the stresses and the explicit powers of x3 are the only terms which depend on the transverse direction. Hence the stress resultants for the three principal layers
for the three principal layers of the sandwich structure using Equation (5) and substituting the result together with the shell kinematics (1) to (4) into Hamilton’s principle (6) with the variations of the strain energy, work by the external loads and kinetic energy according to Equations (7) to (9) results in a lengthy variational expression. Within this expression, the stresses and the explicit powers of x3 are the only terms which depend on the transverse direction. Hence the stress resultants for the three principal layers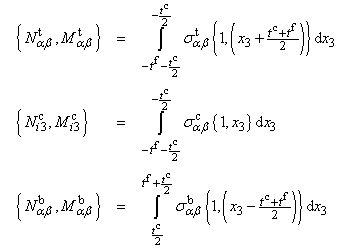 | (10) |
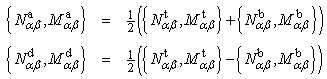 | (11) |
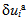 and
and 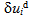 are collected. As a result, a single linear homogeneous equation for the virtual displacements is obtained. Since the virtual displacements are arbitrary and independent, the corresponding coefficients must vanish independently.From the coefficients in the area integral, the equations of motions
are collected. As a result, a single linear homogeneous equation for the virtual displacements is obtained. Since the virtual displacements are arbitrary and independent, the corresponding coefficients must vanish independently.From the coefficients in the area integral, the equations of motions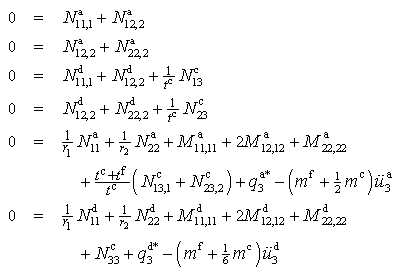 | (12) |
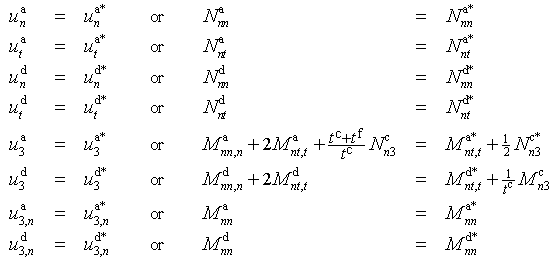 | (13) |
2.4. Material Model
- In the present study, sandwich panels with laminated, infinite fibre reinforced face sheets and orthotropic cores are considered. The two face sheets are assumed to be identical and symmetric with respect to their individual central surface. Hence, their material response is defined by
 | (14) |
 and
and 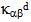 respectively. The components of the
respectively. The components of the 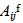 and
and 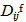 matrices are determined in the usual manner from the integration of the components of the reduced stiffness matrices of the individual plies of the face sheets.For the linear elastic, orthotropic core, the material equations are derived in a similar manner. The material response is defined by
matrices are determined in the usual manner from the integration of the components of the reduced stiffness matrices of the individual plies of the face sheets.For the linear elastic, orthotropic core, the material equations are derived in a similar manner. The material response is defined by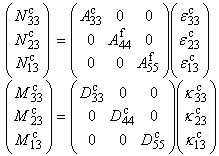 | (15) |
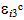 and
and 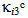 are the mid-plane strains and curvatures of the core. The matrix coefficients are determined similar as for the face sheets.
are the mid-plane strains and curvatures of the core. The matrix coefficients are determined similar as for the face sheets. 3. Solution Procedure
- With the kinematic relations (1) to (5), the material equations (14) and (15), the equations of motion (12) and the boundary conditions (13), a complete set of equations for the dynamic problem of doubly curved sandwich panels is available. Since the problem in general cannot be solved in closed form, a numerical solution procedure is required. In order to be able to perform parametric studies in a numerically efficient manner, the present study employs an extended Galerkin procedure for the solution.For this purpose, the following considerations are restricted to plane or doubly curved sandwich shells with rectangular projection with edge lengths l1 and l2 with respect to the x1 and x2-directions. Furthermore, the study is restricted to sandwich shells which are simply supported along all external boundaries. In this case, the form
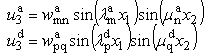 | (16) |
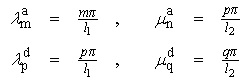 | (17) |
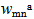 and
and 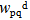 of the transverse displacements.Following the concept of the extended Galerkin procedure, the assumption (16) and (17) for the transverse displacements together with a similar assumption for the virtual transverse displacements
of the transverse displacements.Following the concept of the extended Galerkin procedure, the assumption (16) and (17) for the transverse displacements together with a similar assumption for the virtual transverse displacements 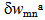 and
and 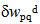 and together with the consistent solution for the in-plane displacements is substituted into Hamilton’s principle (6) together with the expressions (7) to (8) for the individual virtual energy terms and the stress resultants (10) and (11). The stress resultants are expressed through the material equations (14) and (15) in terms of the strains and curvatures of the three principal layers which are substituted with the displacement expressions in terms of the modal amplitudes using the kinematic relations (5) together with Equations (1) to (4). As a result a single homogeneous linear equation for the two virtual modal amplitudes
and together with the consistent solution for the in-plane displacements is substituted into Hamilton’s principle (6) together with the expressions (7) to (8) for the individual virtual energy terms and the stress resultants (10) and (11). The stress resultants are expressed through the material equations (14) and (15) in terms of the strains and curvatures of the three principal layers which are substituted with the displacement expressions in terms of the modal amplitudes using the kinematic relations (5) together with Equations (1) to (4). As a result a single homogeneous linear equation for the two virtual modal amplitudes 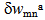 and
and 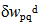 is obtained. Since the virtual modal amplitudes are arbitrary and independent from each other, the corresponding coefficients must vanish independently, yielding a set of two coupled second order differential equations for the unknown modal amplitudes wmna and wpqd as a function of time. In contrast to previous studies based on a v. Kármán type nonlinear approach (Hohe and Librescu[5],[6]), a much more simple linear system is obtained since all geometrical nonlinearities were discarded in the present study.The system may be solved as an initial value problem, similar as in preceding studies (e.g. Hohe et al.[7]). In the present study concerning the free vibrations of sandwich structures, a different approach is employed. Assuming harmonic oscillations, the modal amplitudes may be postulated in the form
is obtained. Since the virtual modal amplitudes are arbitrary and independent from each other, the corresponding coefficients must vanish independently, yielding a set of two coupled second order differential equations for the unknown modal amplitudes wmna and wpqd as a function of time. In contrast to previous studies based on a v. Kármán type nonlinear approach (Hohe and Librescu[5],[6]), a much more simple linear system is obtained since all geometrical nonlinearities were discarded in the present study.The system may be solved as an initial value problem, similar as in preceding studies (e.g. Hohe et al.[7]). In the present study concerning the free vibrations of sandwich structures, a different approach is employed. Assuming harmonic oscillations, the modal amplitudes may be postulated in the form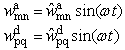 | (18) |
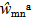 and
and 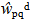 are the amplitudes and
are the amplitudes and 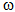 is a constant. Substituting Equation (18) into the governing system for the amplitudes wmna and wpqd constitutes a system of the type
is a constant. Substituting Equation (18) into the governing system for the amplitudes wmna and wpqd constitutes a system of the type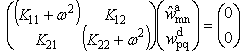 | (19) |
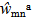 and
and 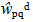 can only exist, if the determinant of the system matrix vanishes. Hence, the natural frequency
can only exist, if the determinant of the system matrix vanishes. Hence, the natural frequency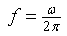 | (20) |
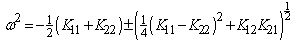 | (21) |
4. Examples
4.1. Validation
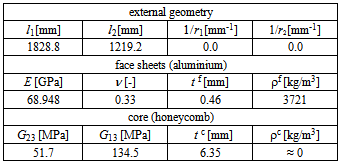
- In a first application, the model is validated against experimental results from literature. In their now classical study, Raville and Ueng[11] have reported measurements of the first natural frequencies for simply supported plane rectangular sandwich plates. The panel consists of isotropic aluminium face sheets bonded to a honeycomb core. The geometry and the material properties are summarized in Table 1.
|
4.2. Plane Sandwich Plates
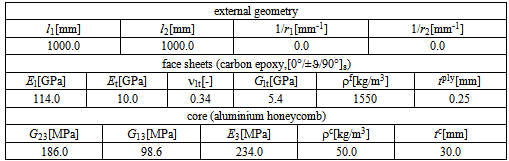
- To study the effect of core and face sheet anisotropy on the natural frequencies and the corresponding eigenmodes, the structural sandwich model is applied in parametric studies concerning different types of sandwich structures. As a first example, a plane square sandwich plate is considered. The plate is assumed to consist of laminated carbon epoxy face sheets with eight plies in a symmetric[0°/±ϑ/90°]s stacking sequence. The material data is chosen such that the material is characteristic for a carbon epoxy material with approximately 50% fibre volume fraction as it might be processed by a resin transfer moulding process which becomes increasingly popular for industrial scale applications e.g. in the automotive industry. The core material is chosen in the characteristic range for aluminium honeycomb core with anisotropic transverse shear properties. The geometry and material data chosen as a starting point for the parametric studies is summarized in Table 2.
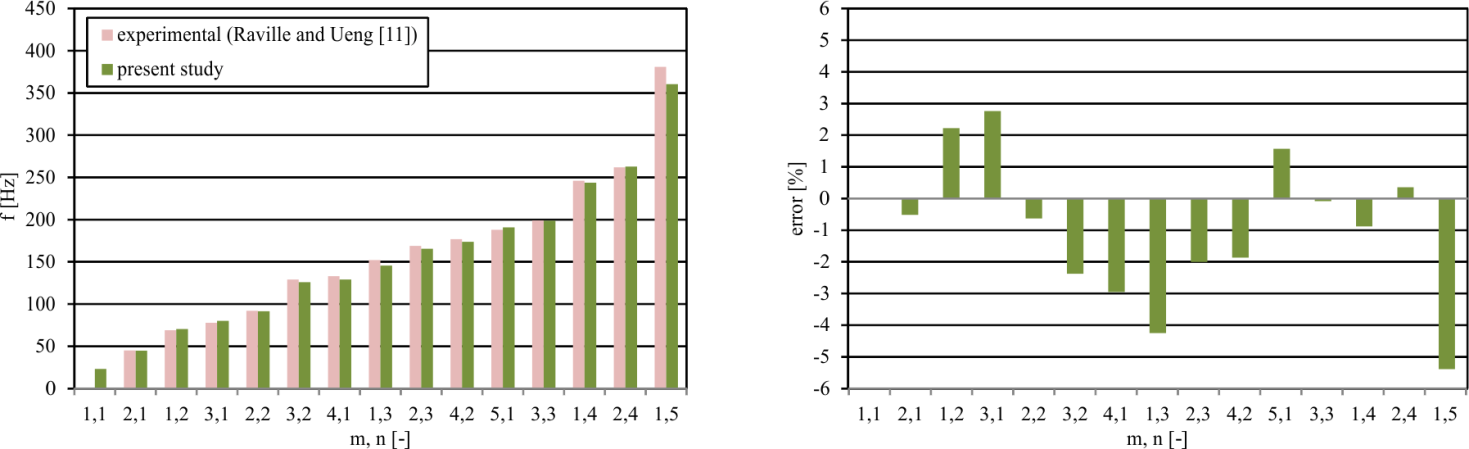 | Figure 2. Validation |
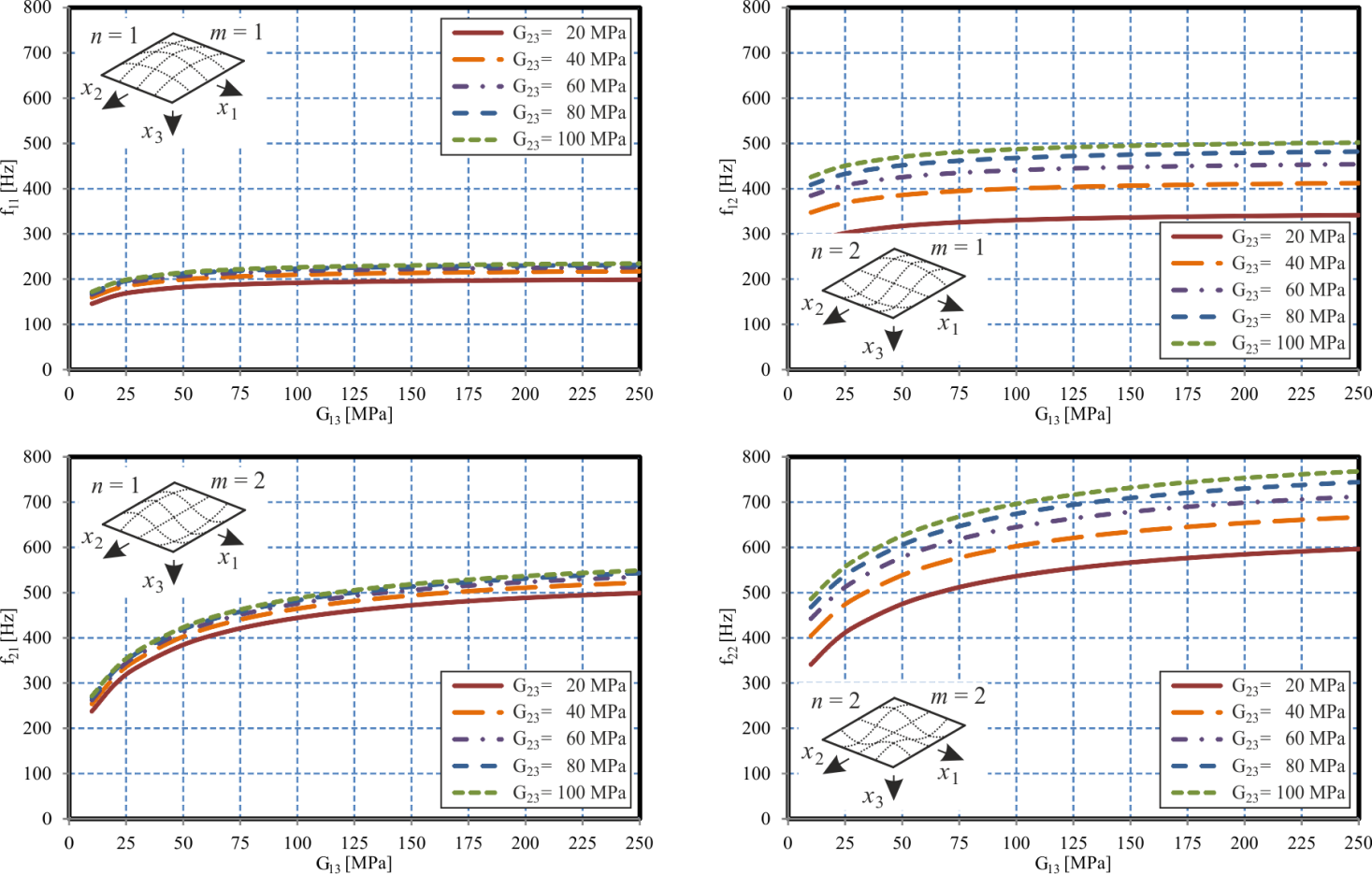 | Figure 3. Plane Sandwich Panel – Effect of the Transverse Core Stiffness |
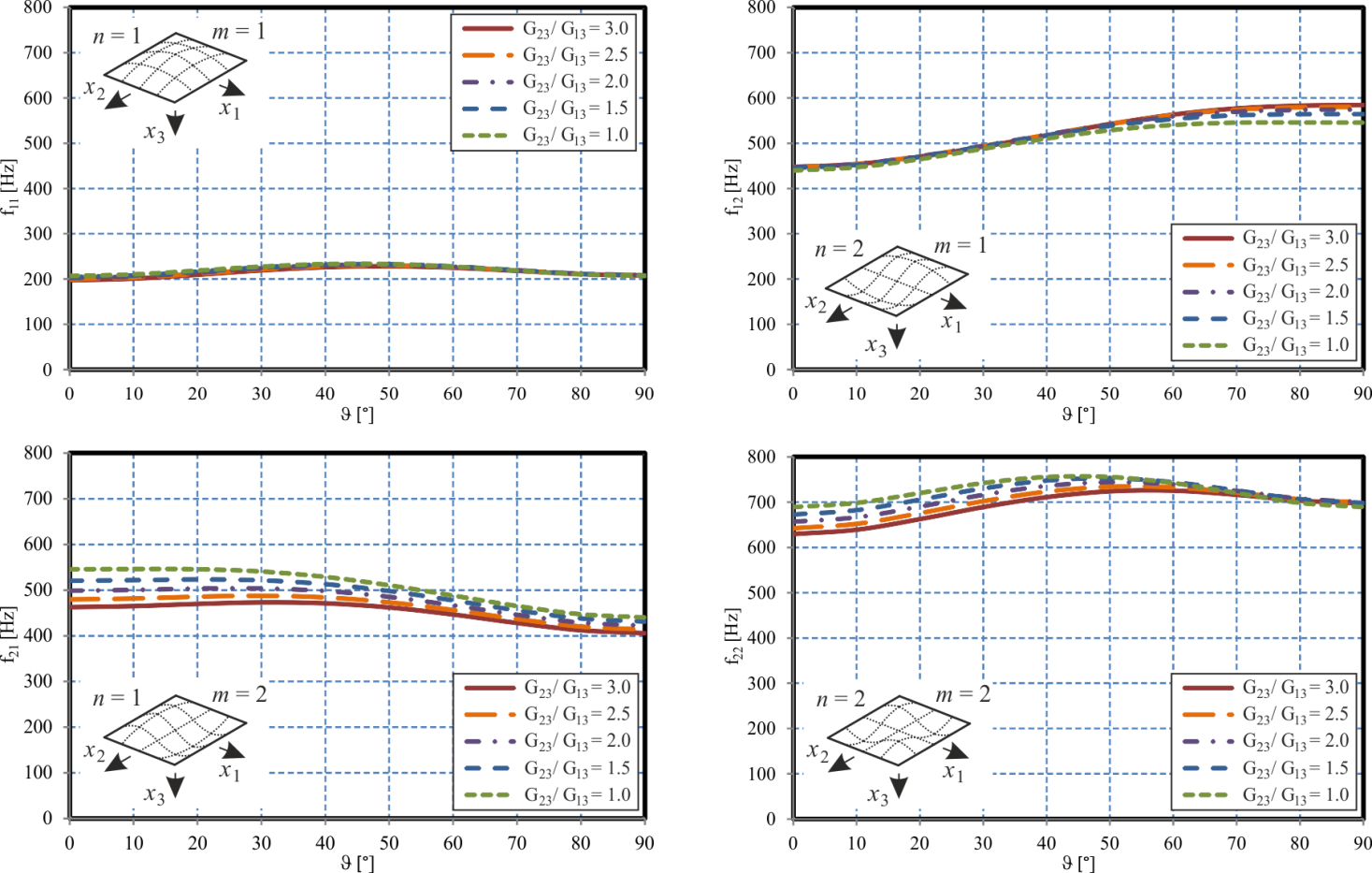 | Figure 4. Plane Sandwich Panel – Effect of the Core and Face Sheet Anisotropy |
|
 0. In this case, the core loses its stiffness so that the limit case of two uncoupled laminated plates is approached. Due to the decreased stiffness, the eigenfrequencies decrease as well. For large transverse shear moduli G23 and G13, the increasingly stiff core requires an increasing amount of in-plane stretching and compression of the face sheets, since the increasing transverse core stiffness increasingly constrains the relative lateral displacements of the face sheets whereas in the weak core limit with vanishing transverse core stiffness, the two face sheets may bend with respect to their individual mid-surfaces rather than with respect to the mid-surface of the entire sandwich structure as in the strong core limit. Depending on the anisotropy of the core, a different order of the four eigenmodes with respect to the corresponding eigenfrequencies develops. In this context, e.g. for G23 = 100 MPa and small G13, f21 is the second natural frequency whereas f12 is the third one. For G13 > 100 MPa and thus G13 > G23, the two eigenfrequencies exchange their roles and f12 becomes the second eigenfrequency whereas f21 becomes the third one. Hence, for standard honeycomb cores with non-isotropic transverse shear moduli, care has to be taken with respect to its assembly direction since a rotated assembly of the core might affect the order of the natural frequencies and thus might result in another eigenmode to become the critical one.In the next parametric study, the effect of the core and face sheet anisotropy is studied in more detail. For this purpose, the fibre angle ϑ is varied over the entire interval[0°, 90°]. In this context, ϑ= 0° constitutes a face sheet layup with six layers orientated towards the x1-direction and only two layers within the x2-direction. Hence, for ϑ = 0°, the x1-direction is the strong direction whereas x2 is the weaker direction. For ϑ= 90°, the directions exchange their roles. The case ϑ = 45° constitutes the case of quasi-isotropic face sheets. Five different ratios G23/G13 for the transverse shear moduli are considered, where the two shear moduli are chosen such that the average transverse shear modulus is (G23 + G13)/2 = 140 MPa. Again, a plane sandwich plate with all other properties according to Table 2 is considered.The results are presented in Figure 4. For the first eigenmode corresponding to the natural frequency f11, only minor effects of the anisotropy of the core and the face sheets are observed. The eigenfrequency f12 increases with increasing fibre angle ϑ and thus increasing stiffness within the x2-direction forming the direction with two sine half waves (and thus the direction with the shorter modal wave length). The opposite effect is observed for the eigenfrequency f21, since in this case, the number of modal waves within the x1- and x2-directions have been exchanged. Due to the core anisotropy the curves for these two eigenmodes are not obtained as mirror image of each other, except for the case G23/G13 = 1, when the core becomes isotropic. Again, it is observed that the natural frequencies f12 and f21 exchange their order depending on the core and face sheet anisotropy. Hence, care has to be taken in an optimization of the laminate stacking sequences for an improvement of either the stiffness or static strength of the structure, since a variation in the anisotropy of the structure – although possibly advantageous for the static response – might have disadvantageous effects on the dynamic response. Especially, eigenmodes, which were initially non critical might become the leading ones. The effect of the core anisotropy on the natural frequencies depends on the eigenmode considered. As it can be observed in Figure 4, the core anisotropy ratio G23/G13 has a stronger influence on the eigenfrequencies for the two modes with m = 2, compared to the other two modes. Since in the current parametric study, G23 is larger than G13 (except for G23/G13 = 1), the x2-direction is the direction supplied with an increasing stiffness with increasing deviation of the anisotropy ratio from G23/G13 = 1. On the other hand, compared to the modes with m = 1, the eigenmodes with m = 2 feature a shorter modal wave length within the x2-direction. Thus, an increasing core shear stiffness towards this direction results in an increasingly constrained deformation, causing the stronger effects of G23/G13 observed in Figure 4 for f21 and f22.
0. In this case, the core loses its stiffness so that the limit case of two uncoupled laminated plates is approached. Due to the decreased stiffness, the eigenfrequencies decrease as well. For large transverse shear moduli G23 and G13, the increasingly stiff core requires an increasing amount of in-plane stretching and compression of the face sheets, since the increasing transverse core stiffness increasingly constrains the relative lateral displacements of the face sheets whereas in the weak core limit with vanishing transverse core stiffness, the two face sheets may bend with respect to their individual mid-surfaces rather than with respect to the mid-surface of the entire sandwich structure as in the strong core limit. Depending on the anisotropy of the core, a different order of the four eigenmodes with respect to the corresponding eigenfrequencies develops. In this context, e.g. for G23 = 100 MPa and small G13, f21 is the second natural frequency whereas f12 is the third one. For G13 > 100 MPa and thus G13 > G23, the two eigenfrequencies exchange their roles and f12 becomes the second eigenfrequency whereas f21 becomes the third one. Hence, for standard honeycomb cores with non-isotropic transverse shear moduli, care has to be taken with respect to its assembly direction since a rotated assembly of the core might affect the order of the natural frequencies and thus might result in another eigenmode to become the critical one.In the next parametric study, the effect of the core and face sheet anisotropy is studied in more detail. For this purpose, the fibre angle ϑ is varied over the entire interval[0°, 90°]. In this context, ϑ= 0° constitutes a face sheet layup with six layers orientated towards the x1-direction and only two layers within the x2-direction. Hence, for ϑ = 0°, the x1-direction is the strong direction whereas x2 is the weaker direction. For ϑ= 90°, the directions exchange their roles. The case ϑ = 45° constitutes the case of quasi-isotropic face sheets. Five different ratios G23/G13 for the transverse shear moduli are considered, where the two shear moduli are chosen such that the average transverse shear modulus is (G23 + G13)/2 = 140 MPa. Again, a plane sandwich plate with all other properties according to Table 2 is considered.The results are presented in Figure 4. For the first eigenmode corresponding to the natural frequency f11, only minor effects of the anisotropy of the core and the face sheets are observed. The eigenfrequency f12 increases with increasing fibre angle ϑ and thus increasing stiffness within the x2-direction forming the direction with two sine half waves (and thus the direction with the shorter modal wave length). The opposite effect is observed for the eigenfrequency f21, since in this case, the number of modal waves within the x1- and x2-directions have been exchanged. Due to the core anisotropy the curves for these two eigenmodes are not obtained as mirror image of each other, except for the case G23/G13 = 1, when the core becomes isotropic. Again, it is observed that the natural frequencies f12 and f21 exchange their order depending on the core and face sheet anisotropy. Hence, care has to be taken in an optimization of the laminate stacking sequences for an improvement of either the stiffness or static strength of the structure, since a variation in the anisotropy of the structure – although possibly advantageous for the static response – might have disadvantageous effects on the dynamic response. Especially, eigenmodes, which were initially non critical might become the leading ones. The effect of the core anisotropy on the natural frequencies depends on the eigenmode considered. As it can be observed in Figure 4, the core anisotropy ratio G23/G13 has a stronger influence on the eigenfrequencies for the two modes with m = 2, compared to the other two modes. Since in the current parametric study, G23 is larger than G13 (except for G23/G13 = 1), the x2-direction is the direction supplied with an increasing stiffness with increasing deviation of the anisotropy ratio from G23/G13 = 1. On the other hand, compared to the modes with m = 1, the eigenmodes with m = 2 feature a shorter modal wave length within the x2-direction. Thus, an increasing core shear stiffness towards this direction results in an increasingly constrained deformation, causing the stronger effects of G23/G13 observed in Figure 4 for f21 and f22.4.3. Curved Sandwich Shells
- In further parametric studies, the effect of the anisotropy of the honeycomb core and the composite face sheets on curved sandwich structures is investigated. Both, cylindrical sandwich shells with either ρ1 = 1/r1 ≠ 0 or ρ2 = 1/r2 ≠ 0 (and the other radius equal to zero) and doubly curved sandwich shells with both ρ1 ≠ 0 and ρ2 ≠ 0 are analysed.
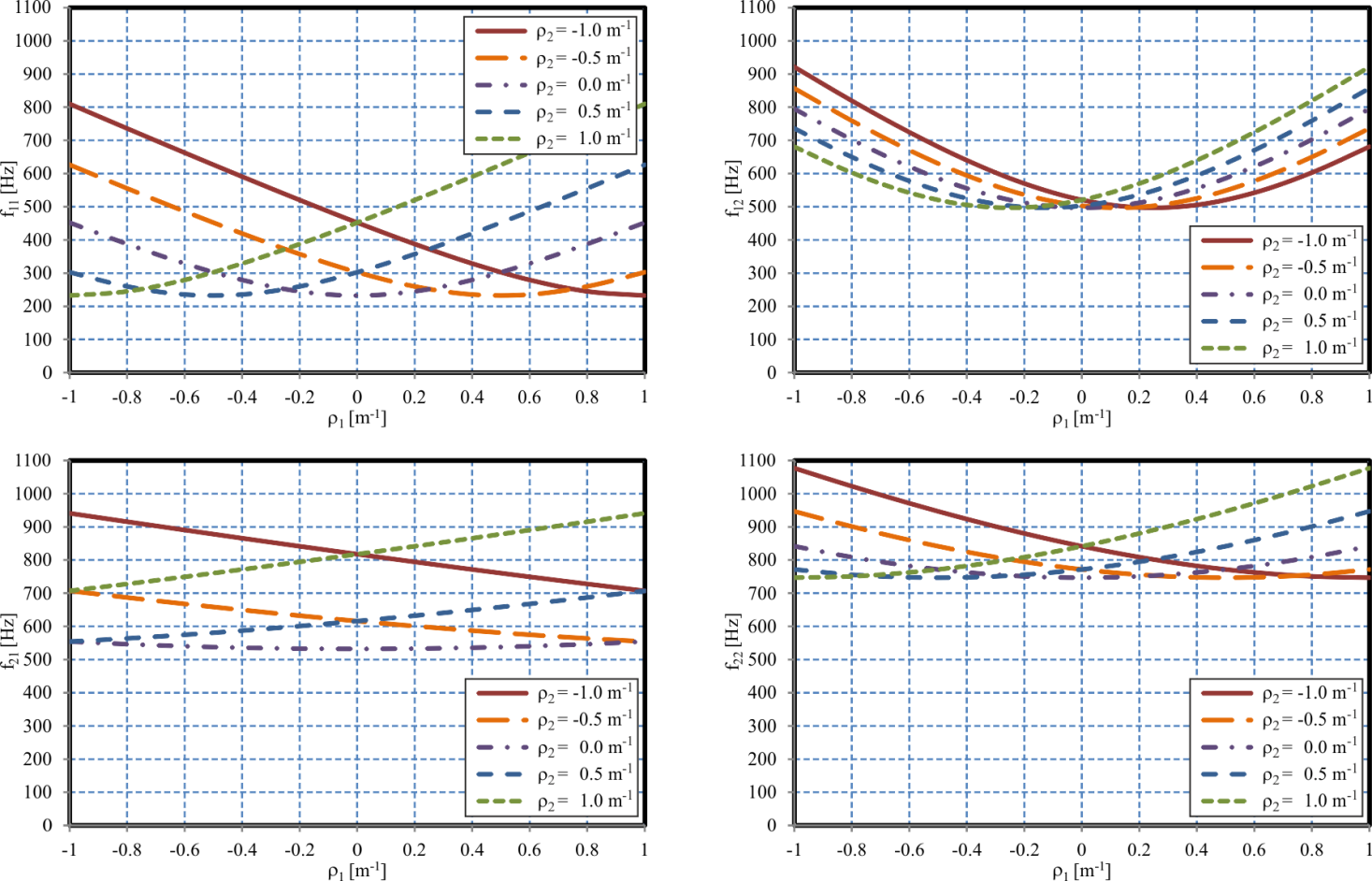 | Figure 5. Doubly Curved Sandwich Shell – Effect of the Curvature |
 | Figure 6. Doubly Curved Geometries |
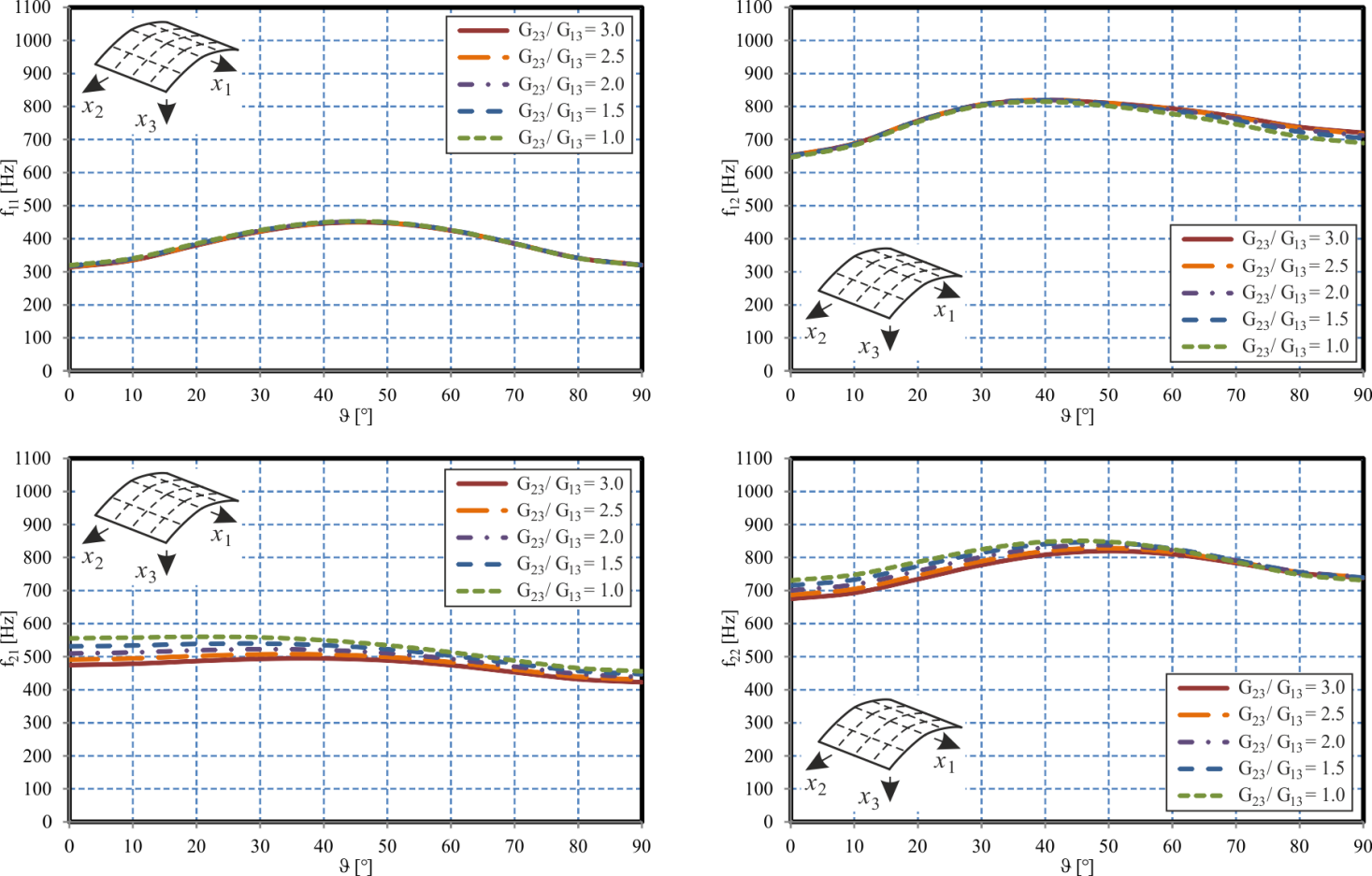 | Figure 7. Cylindrical Sandwich Shell – Effect of Core and Face Sheet Anisotropy |
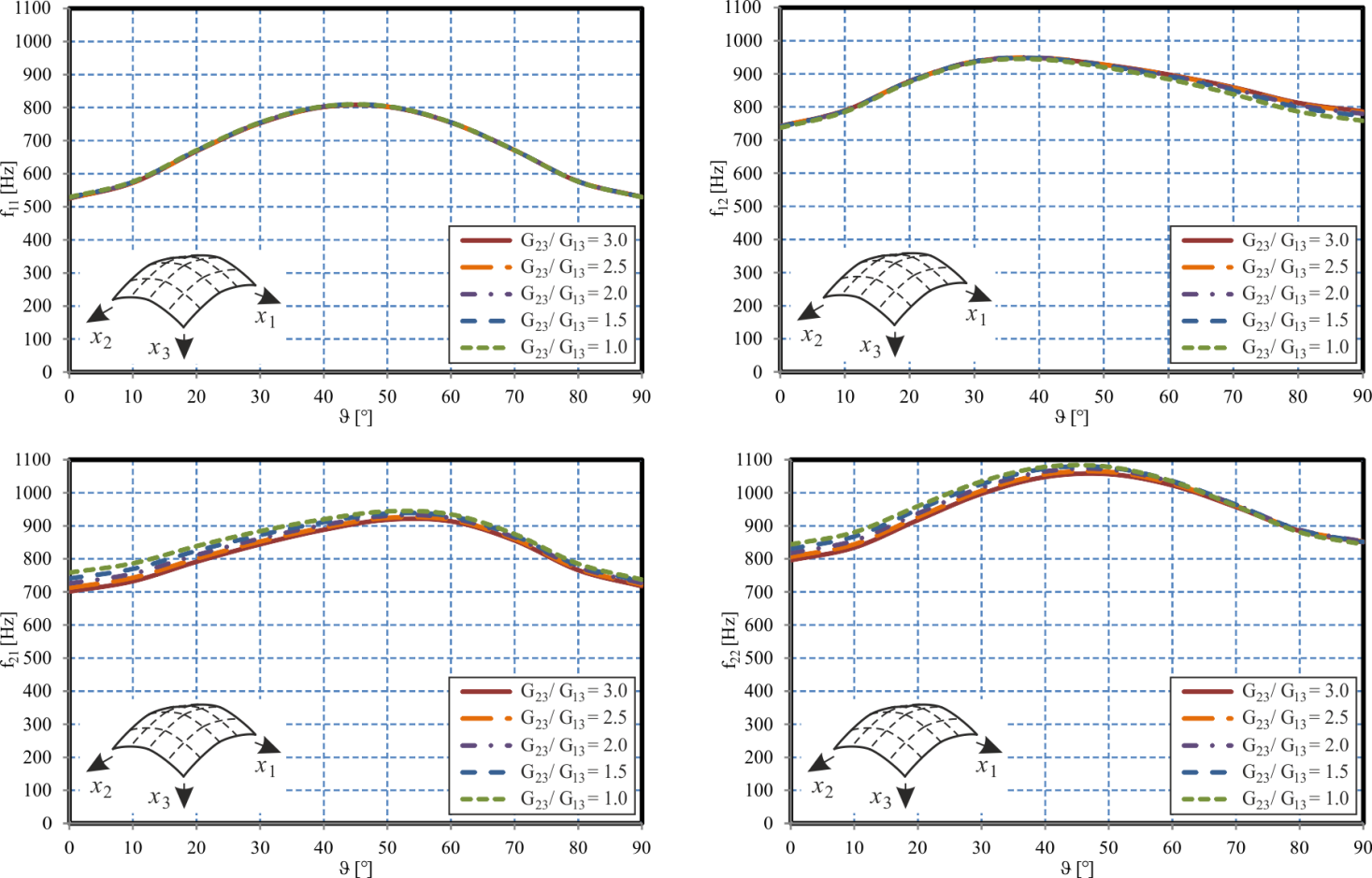 | Figure 8. Spherical Sandwich Cap – Effect of the Curvature |
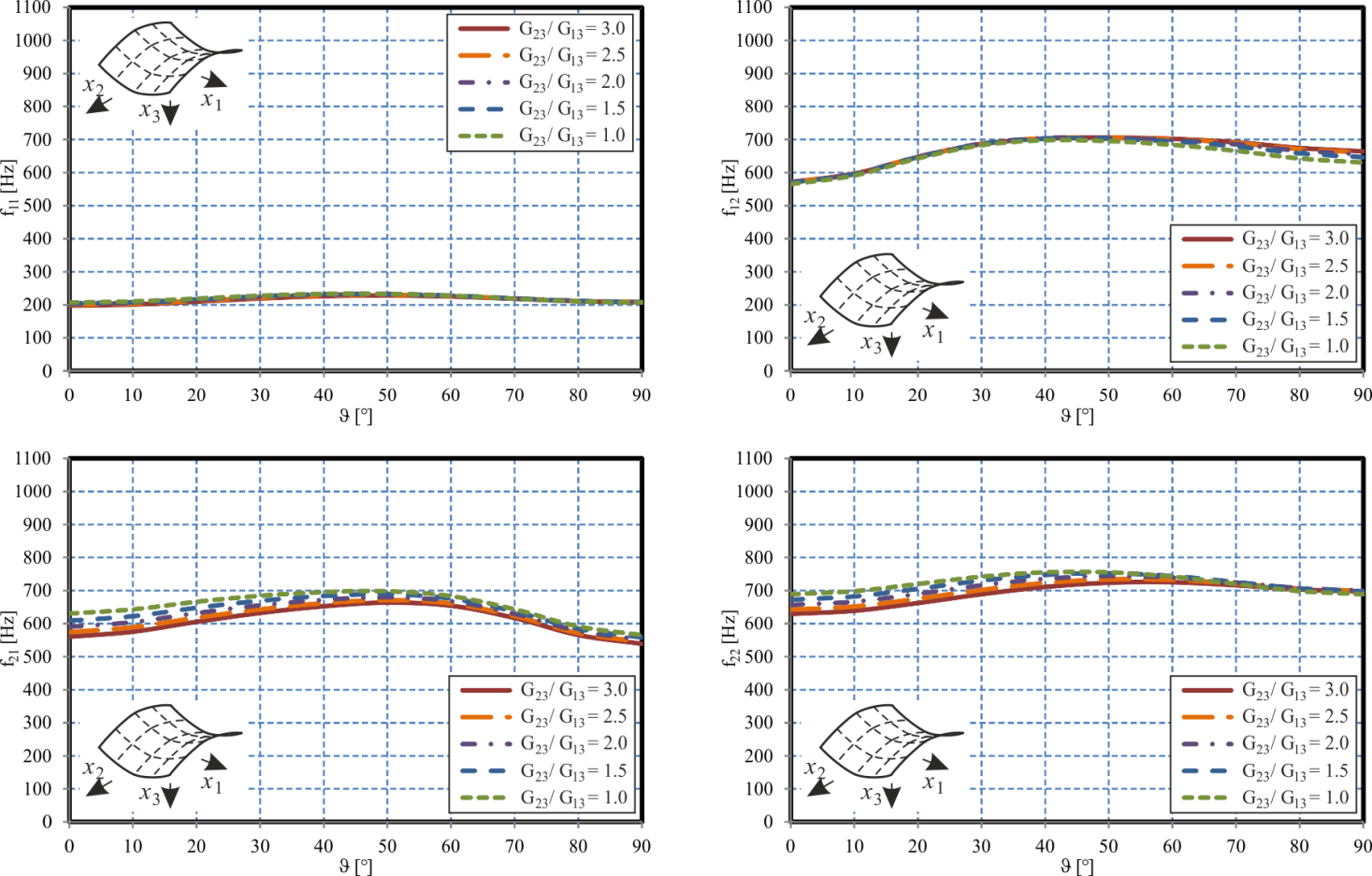 | Figure 9. Sandwich Saddle Shell – Effect of Core and Face Sheet Anisotropy |
5. Conclusions
- The present study is concerned with a numerical analysis of the effect of the anisotropy of core and composite face sheets on the free vibration of plane and curved sandwich plates and shells. For the analysis, a simplified, geometrically linear reformulation of a previous, more general sandwich shell theory is utilized. The model is based on the Kirchhoff-Love model for the face sheets and a second/first order power-series expansion of the core displacements. Consistent equations of motion and boundary conditions are derived by means of Hamilton’s variational principle.For the case of simply supported sandwich plates or shells with rectangular projection, an analytical solution is derived by means of an extended Galerkin procedure. Assuming harmonic oscillations, an eigenvalue problem is obtained, governing the natural frequencies. In a validation against experimental data from literature, the model proves to be accurate and numerically extremely efficient, making it a powerful tool for a fast execution of parametric studies concerning the natural frequencies and corresponding eigenmodes of the considered class of sandwich structures.The model is applied in parametric studies regarding the effect of fibre angles of the composite laminated face sheets and the anisotropy in the transverse shear moduli of the core on the lower natural frequencies of sandwich structures. It is observed that the natural frequencies are affected in a complex combined manner by structural stiffness effects due to the shell curvatures together with the anisotropy in the material stiffness of the principal layers. It is observe that the leading eigenmodes of the free vibration might distinctively be affected by variations in the composite design such as variation in the composite lay-up, fibre angles and assembly angle of an anisotropic honeycomb core. The significance of the effect depends in a complicated manner on the interactions of structural stiffness induced e.g. by panel curvatures and the material stiffness distribution. Hence, care has to be taken when optimizing the composite stacking sequence and fibre angles for the objective of overall static stiffness and strength, since variations in the composite material design may affect the first natural frequencies and may even result in changes in the leading critical eigenmodes.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML