-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2013; 3(6B): 1-9
doi:10.5923/s.cmaterials.201310.01
Modal-Based Non-Destructive Damage Assessment in Composite Structures Using Wavelet Analysis: A Review
Andrzej Katunin
Institute of Fundamentals of Machinery Design, Silesian University of Technology, Gliwice, 44-100, Poland
Correspondence to: Andrzej Katunin , Institute of Fundamentals of Machinery Design, Silesian University of Technology, Gliwice, 44-100, Poland.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The paper presents an overview and a history of development of non-destructive modal-based methods together with advanced signal processing techniques based on wavelet transform applied to the composite fiber-reinforced materials. The wavelet analysis applied for the structural damage assessment gains the popularity due to the high sensitivity to any non-continuities and singularities in the measurement signals, therefore the wavelet-based methods could be used to evaluate the condition of the structure without destruction and even, in the most cases, without contact with a structure. Another great advantage of the wavelet-based methods is an ability of the structure condition evaluation without the reference healthy structure or the model of such a structure. This review summarizes the algorithms used for the damage detection, localization and identification, discusses the crucial factors, which have an influence on the sensitivity and localization accuracy of these methods and indicates the main problems, both mathematical and experimental, which occurs during the application of wavelet-based methods.
Keywords: Wavelet Analysis, Non-destructive Damage Assessment, Polymeric Composites, Fiber-reinforced Materials
Cite this paper: Andrzej Katunin , Modal-Based Non-Destructive Damage Assessment in Composite Structures Using Wavelet Analysis: A Review, International Journal of Composite Materials, Vol. 3 No. 6B, 2013, pp. 1-9. doi: 10.5923/s.cmaterials.201310.01.
Article Outline
1. Introduction
- Wide application of polymeric composites in civil and mechanical engineering, especially in aircraft, aerospace, ship-building and automotive industries, created the necessity of development of suitable structural diagnostic methods and tools, which will be applicable to the heterogeneous materials. Due to the increasing requirements to the technical condition of composite structural elements in above-mentioned industries the diagnostic methods should fulfill several conditions: they should be non-destructive and possibly non-contact, they should be sensitive to the various types of damages occurred in the fibrous composites and should provide the damage detection in possibly early stage of the damage propagation, and finally they should allow for conducting the tests in environmental conditions and be low-cost. The modal-based methods together with advanced signal processing techniques in the most cases satisfy all of these requirements.The classical modal analysis, i.e. the analysis of eigenfrequencies and modal shapes, could detect only the large damages, which confirms several studies[1-5]. Considering a fact, that the polymeric fibrous composites are characterized by the high variability of their mechanical properties and a fact, that a lot of factors may influence on these properties (e.g. changes of the environmental and workload conditions) the analysis of eigenfrequencies in not effective in the damage assessment in these materials. The frequency response functions (FRF) should be compared with FRFs of healthy structures or with FRFs obtained from analytical or numerical models. Moreover, these methods could not be used for the estimation of the damage location.The great potential of the modal-based method was introduced, when the modal shapes of vibration were used for the damage assessment. Several studies in this area (see e.g.[6]) simply analysed the changes in curvatures of modal shapes, used statistical measures in order to evaluate the damage presence[7,8] or analysed the strain energy[9]. The analysis of raw modal shapes allows for localization of damages, but only when these damages were relatively large. In order to detect and localize the damages an additional signal processing tool applied for the modal shapes was necessary. Among other methods, including analysis of random decrement signatures[10], Hilbert-Huang transform [11], genetic algorithm-based optimization used for damage detection[12], temperature analysis and Poincaré maps of damaged structures[13], a group of the most promising techniques is the wavelet-based analysis. A brief overview of the wavelet-based methods used for damage assessment in structural elements was presented in the further section.
2. Development of the Wavelet-Based Damage Assessment Methods
2.1. Brief Overview of Wavelets and Wavelet Transforms
- The first wavelets were introduced by Haar in[14] and named after him. Although the new transform was introduced, its application was limited to the mathematical analysis. The next transform and fundamentals of the continuous wavelet transform (CWT) was introduced by Gabor. He proposed the wavelets[15] named later after him and known as Gabor wavelets or Gabor atoms. Later, Grossmann and Morlet introduces CWT in[16,17]. Several wavelets dedicated for CWT (non-orthogonal and/or with infinite support) were developed in the next period: the real-valued (e.g. Meyer wavelet, Mexican hat wavelet, Shannon wavelet, etc.) and the complex-valued (e.g. Morlet wavelet).The revolution in wavelets practical application and their popularization in almost every branch of science, which uses technical computing and data analysis methods, was introduced by Daubechies. She proposed a new class of orthonormal wavelets[18,19] named after her and introduced the discrete wavelet transform (DWT), which based on the multiresolution framework introduced by Mallat[20]. Several varieties of the Daubechies wavelets were developed later by her scientific group: the coiflets designed by Daubechies on the request of Coifman[19,21], symlets, which are the modified form with increased symmetry of the original Daubechies wavelets[19],Cohen-Daubechies-Feauveau wavelets, which were the first biorthogonal wavelets [19,22], etc. At the same period Chui and Wang developed a class of compactly supported B-spline wavelets[23,24].In the last two decades, due to the increasing application of wavelets (primarily in signal and image processing in graphics and medicine), the development of new transforms and new wavelets could be observed. Holschneider et al.[25] propose the stationary wavelet transform (SWT), a modification of DWT which allows for avoiding of shift-invariance. The new approach was proposed by Sweldens[26]. He constructed an algorithm of DWT with the lifting scheme, i.e. the wavelet design and a transform with use of them is carried out in a single algorithm. This transform is called the lifting wavelet transform (LWT) or the second generation wavelet transform.Currently the topic research on improving the approximation results of the wavelet transforms was carried out. The new class of transforms, the fractional wavelet transforms (FrWT), is under development. Probably the first proposal of FrWT was presented by Unser and Blu[27,28]. They also developed a class of fractional B-spline wavelets, which creates of an infinite number of wavelets with respect to their fractional order and other parameters. Thus, the wavelets of almost arbitrary order could be selected depending necessities in the application domain.
2.2. Algorithms for the Structural Damage Assessment Using Wavelet Transform
- Due to the high sensitivity of wavelet-based methods to the imperfections in the measured vibration signals the great interest to them in structural diagnostics problems has been observed over the last two decades. The first studies on the structural damage detection by the wavelet analysis were carried out during the development of fundamentals of the wavelet theory and multiresolution analysis in early 90. of XX century.Probably the first, who applied the wavelets to the analysis of vibration signals for damage detection purposes, was Surace and Ruotolo[29]. The authors of[30,31] firstly used the spatial wavelet transform based on CWT with a Haar wavelet in order to detect and localize cracks in beams. The first application of DWT for the damage detection in composite laminates was presented in[32]. The authors used Daubechies wavelets for detection of impact damages basing on structural response. This method, however, do not allows for localization of the damages in a structure. Continuing the works presented in[31], the authors of[33] used spatial CWT for damage detection and localization with use of Gabor wavelets. The analysis was performed on numerical model of the beam following the formulation of Timoshenko. From the analysis of vibration signals after performing CWT at different scales the authors show a possibility of precise localization of the modelled crack. Further, the authors generalized the CWT-based method to spatial geometrical domain[34], which allows for the analysis of spatial damages in 2D structures. In[35] they also presented the CWT-based approach for estimation of damage position and relative depth. In all presented works the authors used Gabor wavelets.A slightly different approach was presented by the Greek group. In[36] the authors firstly analysed a type of applied wavelet and indicated that this factor has a great influence on the sensitivity of the wavelet-based methods. Basing on experimental observations they used symlets for the damage detection and localization in beams[36,37] and plates[38,39]. The analysis of damage detection was carried out by Gentile and Messina[40]. They used Gauss wavelets in CWT-based algorithm and analysed the influence of the boundary conditions of beams and the presence of noise on the sensitivity of a proposed method. Interesting studies were presented by the Polish group. Rucka and Wilde presented the studies of damage identification of beams and plates and validated them experimentally[41]. They also presented a comparative study of various wavelets applicable to the investigated problem with respect to specific parameters of wavelets: number of vanishing moments, symmetry and a width of the effective support. Based on this comparative study they selected Gaussian and reversed biorthogonal wavelets as the most effective for the CWT-based damage identification.Another approach was proposed by Zhong and Oyadiji[42]. They used SWT-based method for the crack detection problem and show that the application of SWT with respect to CWT is more computationally efficient. For the analysis they used symlets of order 4, same as the authors of[36]. The authors of[43] combine CWT and DWT in order to develop a new damage detection method, which was based on calculation of the modal assurance criterion. They verified the method experimentally on simply-supported beams with multiple cracks and used the symlets, which were chosen from the analysis of vanishing moments of the compactly supported wavelets. Further, several studies of 2D algorithms based on CWT were performed: Huang et al. use the Mexican hat wavelet[44], while Fan and Qiao[45] used 2D Gaussian wavelet. The researchers started seeking for the ways of improvement of a sensitivity of wavelet-based methods for the damage identification problems and tried to develop novel measures, which estimate the damage presence and position with high precision. The authors of[46] proposed energetic zeroth-order moment approach for the damage identification based on CWT with use of Daubechies wavelets of order 8. The studies of Katunin were concentrated on the development of DWT-based algorithms for the damage identification in composite beams[47,48] and plates[49-51] with use of B-spline wavelets. Regardless to the limitation of DWT, where only the orthogonal compactly supported wavelets could be applied, the application of B-spline wavelets proves the highest sensitivity to the damages with respect to all other compactly supported orthogonal wavelets[49]. It was also proven[51], that DWT is the most effective wavelet transform in comparison with CWT, SWT and LWT, when the appropriate wavelets were selected for the analysis.Recently, the improvement of the damage identification algorithms is based on usage of supporting methods. Rucka and Wilde[52] presented the CWT-based algorithm of the damage detection supported by the artificial neural networks (ANN), Hein and Feklistova[53] used wavelet transform together with ANN for detecting the delaminations in composite beams, while Xiang and Liang[54] presented a two-step algorithm of damage detection, which uses 2D DWT-based algorithm together with particle swarm optimization. Following this, the DWT-based method with use of B-spline wavelets discovered by Katunin was improved by using fractional B-spline wavelets for the structural diagnostics. The application of these wavelets allows for choosing their most suitable parameters in order to improve the sensitivity of the method. Preliminary results of their application to the structural diagnostics problems of composites were presented in[55]. Further studies allows for combining FrWT with genetic algorithm, which was used for selection of optimal parameters of fractional B-spline wavelets[56].Further analysis of damage assessment in composite structures using wavelet-based methods needs an introduction of the fundamentals of a wavelet theory. The main mathematical formulations of this theory will be the topic of the next section.
3. Theoretical Background
- There are two fundamental varieties of the wavelet transforms: CWT and DWT; basing on these varieties other modifications of the wavelet transforms were constructed. In the following section the mechanisms of five above-mentioned transforms will be discussed. The basic formulations in 1D space will be presented, for the description of their 2D analogues see e.g.[51].
3.1. Continuous Wavelet Transform
- The CWT is the oldest wavelet transform based on the integration of square-integrable functions
 in the Hilbert space. This transform convolved the signal with a wavelet function
in the Hilbert space. This transform convolved the signal with a wavelet function  , where
, where  and
and  denote scaling and translation parameters, respectively. The transform could be presented by the following equation:
denote scaling and translation parameters, respectively. The transform could be presented by the following equation: | (1) |
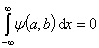 | (2) |
 | (3) |
3.2. Discrete Wavelet Transform
- The DWT was developed mostly by Daubechies in late 80. of XX century basing on the multiresolution signal representation proposed by Mallat in[20]. This representation forms the descending sequence of closed functional spaces
 :
: | (4) |
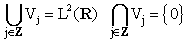 | (5) |
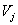 for any
for any 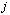 in a space
in a space  is a space with orthonormal base
is a space with orthonormal base 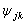 ,
, 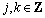 . Thus, there is a limitation for the wavelet and scaling function: they should be orthonormal or (semi-, bi-)orthogonal. During DWT the signal
. Thus, there is a limitation for the wavelet and scaling function: they should be orthonormal or (semi-, bi-)orthogonal. During DWT the signal 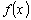 is decomposed to the set of approximation coefficients and the set of detail coefficients in each level of decomposition. The signal could be presented in the following form:
is decomposed to the set of approximation coefficients and the set of detail coefficients in each level of decomposition. The signal could be presented in the following form: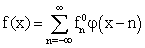 | (6) |
 denotes translation procedure by the scaling function.The DWT-based decomposition could be presented by the set of filters. In this case the resulted sets of approximation and detail coefficients could be presented as:
denotes translation procedure by the scaling function.The DWT-based decomposition could be presented by the set of filters. In this case the resulted sets of approximation and detail coefficients could be presented as: | (7) |
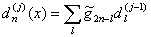 | (8) |
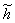 and
and 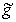 are the impulse responses of the low-pass and high-pass filters, respectively. Due to the downsampling operation during DWT the resulted sets of coefficients have a half length with respect to the original signal in the case of single-level decomposition. Following to the dyadic rule, the resulted length of sets of obtained coefficients reduces twice with each next level of decomposition.
are the impulse responses of the low-pass and high-pass filters, respectively. Due to the downsampling operation during DWT the resulted sets of coefficients have a half length with respect to the original signal in the case of single-level decomposition. Following to the dyadic rule, the resulted length of sets of obtained coefficients reduces twice with each next level of decomposition.3.3. Stationary Wavelet Transform
- The SWT is the redundant transform, i.e. the downsampling procedure during decomposition is omitted. Therefore the decomposition relations (7) and (8) take a form[58]:
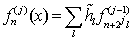 | (9) |
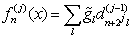 | (10) |
3.4. Lifting Wavelet Transform
- The LWT is a two-step wavelet transform, which started from the decomposition basing on classical DWT and then the lifting procedure is preformed. The lifting is based on the prediction of one of the parts of a signal basing on a set of filters applied for this part according to the fact that these parts are correlated. The decomposition procedure represented by filters is as follows[26]:
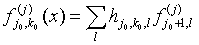 | (11) |
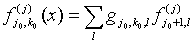 | (12) |
3.5. Fractional Wavelet Transform
- In the FrWT proposed by the authors of[28] the fractional scaling functions are not compactly supported and not symmetric with exceptions, when their order is integer. This implies that they could not be used in DWT. However, the algorithm of FrWT could be constructed basing on Fourier series in order to avoid this problem[27]. The general difference between DWT and FrWT is that the last is defined by filters of fractional order. The orthogonalized high-pass and low-pass filters in z-domain for FrWT are as follows:
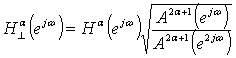 | (13) |
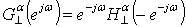 | (14) |
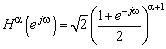 | (15) |
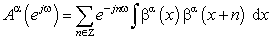 | (16) |
4. Main Factors Influenced on the Proper Damage Assessment
- The damage assessment approaches presented in the previous sections reveal a great variability of wavelet transforms and wavelets applied for the analysis. Besides the algorithm selection problem, there are some problems of data acquisition and post-processing. These problems will be analyzed in the following section.
4.1. Selection of the Wavelet Transform
- From the overview presented in the section 2.2 it could be noticed that the most popular wavelet transform applied for the structural damage assessment problems is the CWT. However, the selected transform is strongly depended on the selected wavelet, which will be discussed later. Thus, the analysis of selection of wavelet transform could be performed on this stage only with respect to the types of applicable wavelets and their computational efficiency.The CWT allows for an application of wide range of wavelets, i.e. there is no limitations as is in the case of DWT. In spite of this, the application of CWT is related to the selection of the proper value of a scale parameter (see e.g.[41,45]), which is evaluated basing on the empirical observations.The limitations of application of DWT come from the requirements of orthonormality or (semi-, bi-)orthogonality of the applied wavelets. However, the DWT provides the lowest time-consuming algorithm in comparison with CWT, SWT and LWT, which is important when the large number of measurement points is considered in the analysis. The comparative study for various wavelet transforms on numerical data was presented in[51].
4.2. Selection of the Suitable Wavelet
- Among the wavelet transform, the selection of suitable wavelet for the analysis is important. In early studies of the wavelet-based damage assessment the wavelets were selected basing on empirical observations[31]. In the next studies[36,60] the number of vanishing moments of a wavelet was used as a measure of wavelet approximation effectiveness. Douka et al.[36] stated that the higher number of vanishing moments causes better performance stability, while Rucka and Wilde[41] observed that the effectiveness of a given wavelet is connected also with the length of its effective support. In this case a compromise should be reached, because the higher value of the length of effective support of a wavelet affected in disturbances on the boundaries of the damage and negatively influences on the accuracy of its localization. In[49] the ratio between the number of vanishing moments and the lengths of effective support was proposed as an indicator for the wavelet effectiveness evaluation. The same values of this ratio were obtained for Daubechies wavelets, symlets and B-spline wavelets. However, an additional factor which influenced on the effectiveness of the wavelet is its symmetry. From the above-mentioned wavelets the B-spline ones have a strict symmetry and thus are the most effective in the damage assessment problems. This fact was conducted both in numerical and experimental studies[49]. Comparing the patterns of vibration modes for the composite square plate using various wavelets it was shown that the B-spline wavelets provide the best filtering during decomposition procedure, i.e. the sets of detail coefficients contain the high-magnitude values only in the locations of damages.
4.3. Number of Measurement Points, Damage Position and Estimation of the Damage Depth
- The number of measurement points, which should be considered during the analysis, creates the next compromise. It is obvious that the larger number of measurement points affected in the higher precision of the damage location, but it also affected in increasing the number of mathematical operations and thus the increase of the measurement and computation time, which has a great influence when the large-area structures are tested. Considering these statements, the number of measurement points should be assumed basing on the expected damage area and the precision to be achieved.The damage position has a great influence on the ability of its localization. In the wavelet transforms, which based on the Mallat’s multiresolution analysis (all of the mentioned above except CWT) the diagnostic information is collected in the sets of detail coefficients, i.e. the modal shape is filtered out and only the singularities of a signal were collected. The sensitivity of the method, i.e. the magnitudes of obtained coefficients strongly depended on the magnitudes of displacements of the modal shapes. Therefore, if the damage is located e.g. near the clamp of an investigated structure the coefficients does not achieve the highest magnitudes and the damage detection will be problematic. Similar situation could happen if the damage location coincides with the node of modal shape, where the magnitudes of displacements are very low. Assuming that the damage position is unknown, the method should be sensitive to the damage in every possible position. In order to avoid this problem the following solution was proposed [49-51]. During the analysis few modes were considered. Then, after performing the wavelet transform, the absolute values of the detail coefficients were determined and all obtained sets of detail coefficients were summed up. The determination of absolute values is necessary in order to avoid the reduction of values of coefficients with different signs. Such a solution amplifies the magnitudes of detail coefficients in the location of the damage by the superimposition of the sets of detail coefficients from various modal shapes of a structure.The estimation of the damage depth during wavelet-based analysis is one of the most difficult tasks. The proposition of crack depth estimation could be found in[36-39]. The authors estimated the relative crack depth basing on two approaches: first approach is based on the analysis of the magnitudes of detail coefficients in the location of the damage and the second one is based on analysis of the energy of a signal. However, there are several factors which influence on the magnitudes of the detail coefficients. As it was mentioned previously, the detail coefficients are depended on the magnitudes of displacements, i.e. in the case of another position of the damage the coefficients reach another values, even if the normalized values are considered. The next factor is the number of considered measurement points: the coefficients will vary if this number will be changed. Finally, the magnitudes of coefficients depend on the applied wavelet. Therefore, the estimation of the damage depth following the approaches presented in[36-39] could be used only for preliminary analysis of the sensitivity of a method and the obtained values do not coincide with real depths of the damages.
4.4. Boundary Effect and the Influence of Measurement Noise
- The boundary effect caused by mathematical specificity of the wavelet transform is an important phenomenon, which may leads to wrong interpretation of the obtained results. Considering that the analysed signals have a finite length the wavelet produces the high-magnitude coefficients at the boundaries of a signal due to the sudden drop to zero-valued magnitude of displacements in these regions. The length of such perturbed coefficients depends on the number of vanishing moments of the applied wavelet.In order to reduce or eliminate this effect several approaches were proposed. The authors of[45] propose to exclude the regions biased by the boundary effect from the evaluation; however such a solution reduces the diagnostic information. There are several methods of reducing the boundary effect, which based on the synthetic signal extension before the wavelet transform and reducing it to the previous size after the transform. The most common and often used methods are zero-padding, constant-padding, reflection, antisymmetric reflection and periodization[61,62]. Another method was proposed in[36,41]. The authors used the cubic spline interpolation of neighbour measurement points in the problem of damage assessment in a polymeric plate. The effectiveness of these methods in application to the damage assessment problem in composite plate was studied in[63]. Obtained results show that the most effective method is the cubic spline interpolation, which almost completely reduces the boundary effect. The methods based on signal extension, however, do not allow for the proper damage detection and identification in the boundary regions of an investigated structure. An alternative solution was proposed by the authors of[64,65]. The proposed algorithm is based on the modification of a wavelet transform by replacement of wavelets on the boundaries by so-called edge or interval wavelets. This allows for avoiding the problem of the boundary effect, but additionally complicates the algorithm.The great influence on the detectibility of the structural damages has a measurement noise. Generally, the wavelet-based damage assessment methods are very sensitive to the noise presence. Several studies were performed in order to investigate this problem. The authors of[36] investigated an influence of the artificially added noise of 1% with respect to the magnitude of a signal. Results show that the detection and identification of damages seems to be problematic and is impossible when the relative value of the noise achieves 5%, as the authors stated. Therefore, they used denoising procedures on experimental data based on spline interpolation. In[39] the authors found that the highest possible noise level is about 78 dB, i.e. if this value is lower than the method proposed by these authors remains insensitive to the damages. It should be noted, that the maximal depth of the investigated damages equalled 50% of the total thickness. The authors of[41] stated that the measurement noise in experimental data does not corrupt the singularities in the sets of coefficients caused by the damage, however the damage depth was relatively large and equal 25% of total thickness of the investigated square plate. The results presented in[49] show that the application of DWT together with B-spline wavelets allow for identification of damages of the depth of 18.9% without any difficulties. Additional analysis of the noise influence on the sensitivity of the wavelet-based method was presented in[51]. It was shown that the damage is still detectable when the noise level is 55 dB. The increasing of the damage detectability for the noised data is possible, when the prefiltering will be applied to the measured signal before the application of wavelet transform.
5. Testing Apparatus
- An overview presented in the section 4.4 shows that the measurement noise has a great influence on the detectibility and accuracy of localization of damages during application of wavelet-based method. The following section discusses the measurement equipment used for the structural analysis.
5.1. Contact Measurement Systems
- The first experimental studies of the damage identification in beams and plates were carried out by the Greek group in[36-39]. Their experimental set-up consisted of electromagnetic vibrator connected with the tested structure and two accelerometers, where the first was used directly for the measurements of displacements and the second – as a reference. Therefore, the classical experimental modal analysis was used. The authors of[41,43,45] also conducted the tests basing on modal analysis principles, but used the modal hammer for the excitation of tested structures. The application of contact measurements presented in these studies causes that the measurement sensors (accelerometers) influence on the natural frequencies and modal shapes. This influence becomes greater when the mass of a sensor is considerable with respect to the mass of the tested structure.
5.2. Non-Contact Measurement Systems
- An interesting approach of the structural damage identification was proposed in[66]. The authors analysed the static deflection profiles of a beam using optical sensing, i.e. the high-resolution camera was registered these profiles.The great improvement of the accuracy of the measurement signals could be obtained by an application of laser vibrometers. The experimental test rigs presented in[47-49] used two laser vibrometers: the scanning one for the high-precision measurements of displacements and the point vibrometer as a reference. Similar equipment was used in[67]. The tested structures were excited by the modal shaker. Such a solution allows for removing the influence of measurement devices on the structure, which additionally improves the accuracy of measurements. However, the surface of the tested structure should be covered by the reflective material, which influence on the measurements.
5.3. Embedded Measurement Systems
- A great potential has the application of various embedded measurement systems. One of the most popular devices embedded into the composite structures is the PZT (piezoceramic transducer) plate or film. Such a solution was used by the authors of[32]. Another solution, which gives high-precision measurements, is the application of guided Lamb waves for the estimation of the damage position. Such systems used an array of PZT sensors/actuators. The application of such systems for the damage assessment in composites was described e.g. in[68]. The authors of[69] proposed the measurement system based on the optical FBG (fiber Bragg grating) sensors. The measurements of displacements were carried out with very high precision and than evaluated using DWT-based algorithm.Above-presented measurement systems allow for measurements of displacements with a very high precision, however it is suitable to use them for structure health monitoring, because the investigated structure should be supplied with such systems on the stage of its manufacturing.
6. Conclusions
- Numerous publications dealing with various approaches of the damage assessment of composite structures have been reviewed. Most of them described the analysing methods, which based on CWT. Nevertheless, the necessity of improvement of precision of the wavelet-based methods cause the development of novel approaches, which based on various types of wavelet transforms, sometimes supported by optimization computational algorithms. The previous studies in the area of wavelet-based structural diagnostics as well as novel approaches were discussed in this review. The five wavelet transforms were described; all of them are currently used in the structural diagnostics problems. The main factors, which have a great importance in the proper damage identification in composites were deeply analysed and the best known solutions were pointed out. Finally, a brief overview of the testing devices used in the structural diagnostics was introduced.The significant advances were made in the last five years both in the development of the wavelet-based damage assessment methodology and the testing methods and procedures. It could be expected that the future development of the wavelet-based methods will straightforward to the hybridization of them with powerful approximation and optimization tools as well as application of new types of wavelet transforms and wavelets. The measurement devices used for the diagnostics probably will lead to the miniaturization and improvement of measurement accuracy. It could be also expected that the wavelet-based methods will be the common ones both in diagnostics as well as in monitoring of composite structures.
ACKNOWLEDGEMENTS
- The research project was financed by the National Science Centre (Poland) granted according the decision no. DEC-2011/03/N/ST8/06205.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML