| [1] | Thompson, W. E., 1986, Analysis of dynamic behavior of roads subject to longitudinally moving loads., HRB, 39, 1-24. |
| [2] | Gbadeyan, J. A., Oni, S. T., 1992, Dynamic response to moving concentrated masses of elastic plates on a non-Winkler elastic foundation., Journal of Sound and Vibration, 154, 343–358. |
| [3] | Kim, S. M., Roesset, J. M., 1998, Moving loads on a plate on elastic foundation., Journal of Engineering Mechanics, 124, 1010–1017. |
| [4] | Cheng, Z. Q., 1999, Kitipornchai S. Membrane analogy of buckling and vibration of inhomogeneous plates., Journal of Engineering Mechanics, 125, 1293–1297. |
| [5] | Chien, R. D., Chen, C. S., 2006, Nonlinear vibration of laminated plates on an elastic foundation., Thin-Walled Structures, 44, 852–860. |
| [6] | Aiello, M. A., Ombres, L., 1994, Buckling and vibrations of unsymmetric laminates resting on elastic foundations under in-plane and shear forces., Computers and Structures, 44, 31–41. |
| [7] | Omurtag, M. H., Kadioglu, F., 1998, Free vibration analysis of orthotropic plates resting on Pasternak foundation by mixed finite element formulation., Computers and Structures, 67, 253–265. |
| [8] | Malekzadeh, K., Khalili, S. M. R., Abbaspour, P., 2010, Vibration of non-ideal simply supported laminated plate on an elastic foundation subjected to in-plane stresses., Composite Structures, 92, 1478-1484. |
| [9] | Liu, G. R., Nguyen Thoi Trung., 2010, Smoothed Finite Element Methods, New York, CRC Press. |
| [10] | [10]Chen, J. S., Wu, C. T., Yoon, S., You, Y., 2001, A stabilized conforming nodal integration for Galerkin mesh-free methods., International Journal for Numerical Methods in Engineering, 50, 435–466. |
| [11] | Liu, G. R., Dai, K. Y., Nguyen, T. T., 2007, A smoothed finite element for mechanics problems., Computational Mechanics, 39, 859–877. |
| [12] | Liu, G.R., Nguyen-Thoi, T., Nguyen-Xuan, H., Dai, K.Y., Lam, K.Y., 2009, On the essence and the evaluation of the shape functions for the smoothed finite element method (SFEM)., International Journal for Numerical Methods in Engineering, 77, 1863-1869. |
| [13] | Liu, G. R., Nguyen-Xuan, H., Nguyen-Thoi, T., 2010, A theoretical study on the smoothed FEM (S-FEM) models: properties, accuracy and convergence rates., International Journal for Numerical Methods in Engineering, 84(10), 1222-1256. |
| [14] | Liu, G. R, Nguyen-Thoi, T., Dai, K. Y., Lam, K. Y., 2007, Theoretical aspects of the smoothed finite element method (SFEM)., International journal for numerical methods in Engineering, 71, 902-930. |
| [15] | Liu, G. R., Nguyen-Thoi, T., Nguyen-Xuan, H., Lam, K. Y., 2009, A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems., Computers and Structures, 87, 14-26. |
| [16] | Nguyen-Thoi, T., Liu, G. R., Nguyen-Xuan, H., Nguyen-Tran, C., 2011, Adaptive analysis using the node-based smoothed finite element method (NS-FEM), Communications in Numerical Methods in Engineering, 27(2), 198-218. |
| [17] | Nguyen-Thoi, T., Liu, G. R., Nguyen-Xuan, H., 2009, Additional properties of the node-based smoothed finite element method (NS-FEM) for solid mechanics problems., International Journal of Computational Methods, 6(4), 633-666. |
| [18] | Liu, G. R., Nguyen-Thoi, T., Lam, K. Y., 2009, An edge-based smoothed finite element method (ES-FEM) for static and dynamic problems of solid mechanics., Journal of Sound and Vibration, 320, 1100-1130. |
| [19] | Nguyen-Thoi, T., Liu, G. R., Nguyen-Xuan, H., 2011, An n-sided polygonal edge-based smoothed finite element method (nES-FEM) for solid mechanics., Communications in Numerical Methods in Engineering, 27(9), 1446-1472. |
| [20] | Nguyen-Thoi, T., Liu, G. R., Lam, K. Y., Zhang, G. Y., 2009, A face-based smoothed finite element method (FS-FEM) for 3D linear and nonlinear solid mechanics problems using 4-node tetrahedral elements., International Journal for Numerical Methods in Engineering, 78, 324–353. |
| [21] | Nguyen-Thoi, T., Phung-Van, P., Luong-Van, H., Nguyen-Van, H., Nguyen-Xuan, H., 2013, A cell-based smoothed three-node Mindlin plate element (CS-MIN3) for static and free vibration analyses of plates., Computational Mechanics, 50(1), 65-81. |
| [22] | Nguyen-Thoi, T., Phung-Van, .P, Thai-Hoang, C., Nguyen - Xuan, H., 2013, A cell-based smoothed discrete shear gap method (CS-DSG3) using triangular elements for static and free vibration analyses of shell structures., International Journal of Mechanical Sciences, 74, 32-45. |
| [23] | Nguyen-Thoi, T., Bui-Xuan, T., Phung-Van, P., Nguyen-Xuan, H., Ngo-Thanh, P., 2013, Static, free vibration and buckling analyses of stiffened plates by CS-FEM-DSG3 using triangular elements., Computers and Structures, 125, 100-113. |
| [24] | Nguyen-Thoi, T., Bui-Xuan, T., Phung-Van, P., Nguyen - Hoang, S., Nguyen-Xuan, H., 2013, An edge-based smoothed three-node Mindlin plate element (ES-MIN3) for static and free vibration analyses of plates., KSCE Journal of Civil Engineering, (accepted). |
| [25] | Phung-Van, P., Nguyen-Thoi, T., Tran V.Loc., Nguyen-Xuan, H., 2013, A cell-based smoothed discrete shear gap method (CS-DSG3) based on the C0-type higher-order shear deformation theory for static and free vibration analyses of functionally graded plates., Computational Materials Science, doi: 10.1016/j.commatsci.2013.06.010. |
| [26] | Nguyen-Xuan, H., Liu G. R., Thai-Hoang, C., Nguyen-Thoi, T., 2009., An edge-based smoothed finite element method with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates., Computer Methods in Applied Mechanics and Engineering, 199, 471-489. |
| [27] | Nguyen-Xuan, H., Liu. G. R., Nguyen-Thoi, T., Nguyen-Tran, C., 2009, An edge – based smoothed finite element method (ES-FEM) for analysis of two–dimensional piezoelectric structures., Smart Materials and Structures, 18(065015), 1-12. |
| [28] | Phung-Van, P., Nguyen-Thoi, T., Le-Din,h T., Nguyen-Xuan, H., 2013, Static, free vibration analyses and dynamic control of composite plates integrated with piezoelectric sensors and actuators by the cell-based smoothed discrete shear gap method (CS-FEM-DSG3)., Smart Materials and Structures, (accepted). |
| [29] | Nguyen-Thoi, T., Liu, G. R., Vu-Do, H. C., Nguyen-Xuan, H., 2009, An edge-based smoothed finite element method (ES-FEM) for visco-elastoplastic analyses of 2D solids using triangular mesh., Computational Mechanics, 45, 23- 44. |
| [30] | Nguyen-Thoi, T., Liu, G. R., Vu-Do, H. C., Nguyen-Xuan, H., 2009, A face-based smoothed finite element method (FS-FEM) for visco-elastoplastic analyses of 3D solids using tetrahedral mesh., Computer Methods in Applied Mechanics and Engineering, 198, 3479-3498. |
| [31] | Tran, T. N., Liu, G. R., Nguyen-Xuan, H., Nguyen-Thoi, T., 2010, An edge-based smoothed finite element method for primal-dual shakedown analysis of structures., International Journal for Numerical Methods in Engineering, 82, 917–938. |
| [32] | Nguyen-Thoi, T., Phung-Van, P., Rabczuk, T., Nguyen-Xuan, H., Le-Van, C., 2013, An application of the ES-FEM in solid domain for dynamic analysis of 2D fluid-solid interaction problems., International Journal of Computational Methods, 10(1), 1340003. |
| [33] | Liu, G. R., Nguyen-Xuan, H., Nguyen-Thoi, T., Xu, X., 2009, A novel Galerkin-like weakform and a superconvergent alpha finite element method (SFEM) for mechanics problems using triangular meshes., Journal of Computational Physics, 228, 4055-4087. |
| [34] | Nguyen-Thoi, T., Phung-Van, P., Rabczuk, T., Nguyen-Xuan, H., Le-Van, C., 2013, Free and forced vibration analysis using the n-sided polygonal cell-based smoothed finite element method (nCS-FEM)., International Journal of Computational Methods, 10(1), 1340008. |
| [35] | Nguyen-Thoi, T., Phung-Van, P., Nguyen-Xuan, X., Thai-Hoang, C., 2012, A cell-based smoothed discrete shear gap method using triangular elements for static and free vibration analyses of Reissner–Mindlin plates., International journal for numerical methods in Engineering, 91, 705-741. |
| [36] | Bletzinger, K. U., Bischoff, M., Ramm, E., 2000, A unified approach for shear-locking free triangular and rectangular shell finite elements., Computers and Structures, 75, 321–334.. |
| [37] | Reddy, J. N., 1997, Mechanics of laminated composite plates – Theory and Analysis, New York, CRC Press. |
| [38] | [38]Phan-Dao, H. H., Nguyen-Xuan, H., Thai, C. H., Nguyen-Thoi, T., Rabczuk, T., 2013, An edge-based smoothed finite element method for analysis of laminated composite plates., International Journal of Computational Methods, 10(1), 1340005. |
| [39] | Reddy, J. N., 2004, Mechanics of Laminated Composite Plates and Shells Theory and Analysis, CRC Press. |
| [40] | Liew, K. M., 1996, Solving the vibration of thick symmetric laminates by Reissner/Mindlin plate theory and the p-Titz method., Journal of Sound and Vibration, 198, 343–360. |
| [41] | Zhen, W., Wanji, C., 2006, Free vibration of laminated composite and sandwich plates using global–local higher-order theory., Journal of Sound and Vibration, 298, 333–349. |
| [42] | Ferreira, A. J. M., Luís, M. S. C., Silvia, B., 2009, A high order collocation method for the static and vibration analysis of composite plates using a first-order theory., Composite Structures, 89(3), 424-432. |
| [43] | Lal, A., Singh, B. N., Kumar, R., 2008, Nonlinear free vibration of laminated composite plates on elastic foundation with random system properties., International Journal of Mechanical Sciences, 50, 1203–1212. |

 ,
,
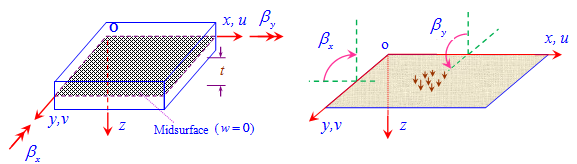
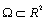 . The displacement field according to Reissner–Mindlin model which based on the first-order shear deformation theory[37] can be expressed by
. The displacement field according to Reissner–Mindlin model which based on the first-order shear deformation theory[37] can be expressed by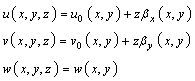
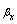 ,
, 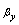 are the rotations of the middle plane around y-axis and x–axis, respectively, with the positive directions defined in Figure 1.The linear strain can be given as
are the rotations of the middle plane around y-axis and x–axis, respectively, with the positive directions defined in Figure 1.The linear strain can be given as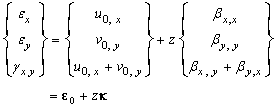
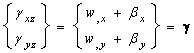

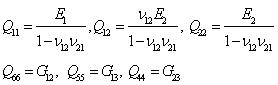

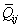 are transformed material constants of the kth lamina as in Ref[37].The Galerkin weakform of transient analysis of composite plates on Pasternak foundation can be written as[8]:
are transformed material constants of the kth lamina as in Ref[37].The Galerkin weakform of transient analysis of composite plates on Pasternak foundation can be written as[8]: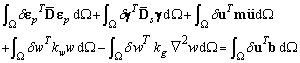
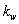 and
and 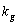 contains the elastic moduli of Pasternak foundation; m is the matrix containing the mass density of the material;
contains the elastic moduli of Pasternak foundation; m is the matrix containing the mass density of the material; 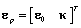 ;
; 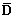 and
and 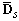 are material constant matrices given in the form of
are material constant matrices given in the form of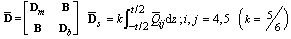
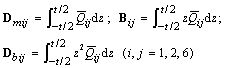
 of the composite plate into
of the composite plate into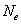 finite elements such that
finite elements such that 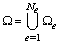 and
and 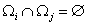 ,
, 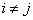 , then the finite element solution
, then the finite element solution 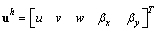 of a displacement model for the composite plate is expressed as
of a displacement model for the composite plate is expressed as
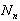 is the total number of nodes of problem domain discretized;
is the total number of nodes of problem domain discretized; 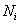 is shape function at ith node;
is shape function at ith node; 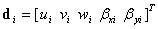 is the displacement vector of the nodal degrees of freedom of
is the displacement vector of the nodal degrees of freedom of 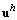 associated to ith node, respectively. The membrane, bending and shear strains can be then expressed in the matrix forms as
associated to ith node, respectively. The membrane, bending and shear strains can be then expressed in the matrix forms as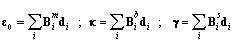
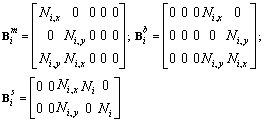
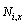 and
and 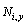 are the derivatives of the shape functions in x-direction and y-direction, respectivelyThe discretized system of equations of composite plates on Pastarnak foundation using the FEM for transient analysis then can be expressed as
are the derivatives of the shape functions in x-direction and y-direction, respectivelyThe discretized system of equations of composite plates on Pastarnak foundation using the FEM for transient analysis then can be expressed as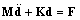
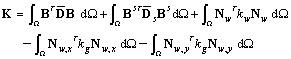
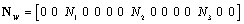 ; B =[Bm Bb] and F, M are the load vector defined by
; B =[Bm Bb] and F, M are the load vector defined by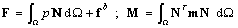
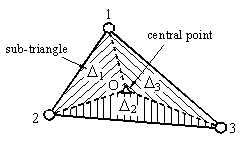
 created from the triangle 1-2-3 in the CS-MIN3 by connecting the central point O with three field nodes 1, 2 and 3
created from the triangle 1-2-3 in the CS-MIN3 by connecting the central point O with three field nodes 1, 2 and 3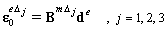
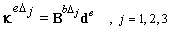
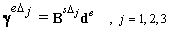
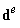 is the vector containing the nodal degrees of freedom of the element;
is the vector containing the nodal degrees of freedom of the element; 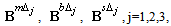 are membrane, bending and shearing gradient matrices by the DSG3[36] of jth sub-triangle, respectively.Now, applying the cell-based strain smoothing operation in the CS-FEM[11], the constant membrane, bending and shear strains
are membrane, bending and shearing gradient matrices by the DSG3[36] of jth sub-triangle, respectively.Now, applying the cell-based strain smoothing operation in the CS-FEM[11], the constant membrane, bending and shear strains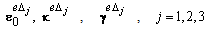 are, respectively, used to create element smoothed strains
are, respectively, used to create element smoothed strains 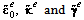 on the triangular element
on the triangular element 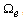 , such as:
, such as: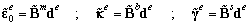
 are the smoothed strain gradient matrices, respectively, given by
are the smoothed strain gradient matrices, respectively, given by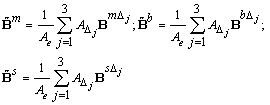
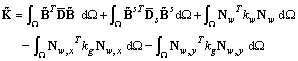
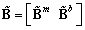
 at the time
at the time 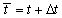 are defined as
are defined as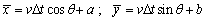
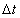 is step time.
is step time.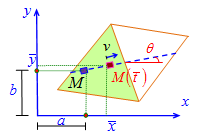
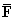 is transformed from the moving mass at the position
is transformed from the moving mass at the position 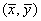 into the load at nodes of elements is defined by
into the load at nodes of elements is defined by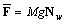
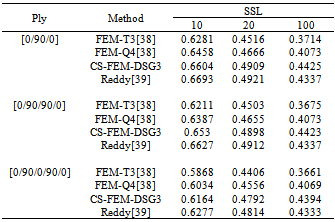
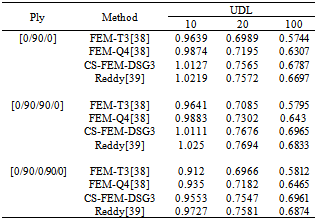
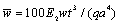 is used. Table 1 and Table 2 display the non-dimensional central node deflection of the simply supported composite plate subjected to SSL and UDL load with ratios length-to-thickness a/t = 10, 20, 100. It is seen that the results by the CS-FEM-DSG3 agree well with those by the Reddy[39] and are better than those of FEM-T3[38] and FEM-Q4[38].
is used. Table 1 and Table 2 display the non-dimensional central node deflection of the simply supported composite plate subjected to SSL and UDL load with ratios length-to-thickness a/t = 10, 20, 100. It is seen that the results by the CS-FEM-DSG3 agree well with those by the Reddy[39] and are better than those of FEM-T3[38] and FEM-Q4[38].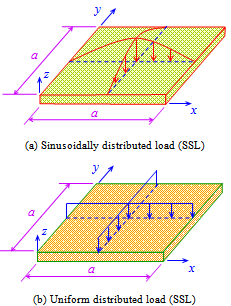
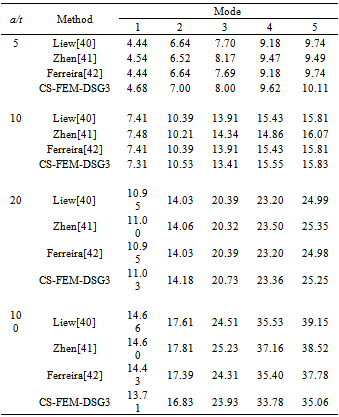
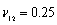 . A non-dimensional frequency parameter
. A non-dimensional frequency parameter 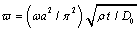 is also used, where
is also used, where 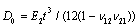 is the flexural rigidity of the plate.
is the flexural rigidity of the plate.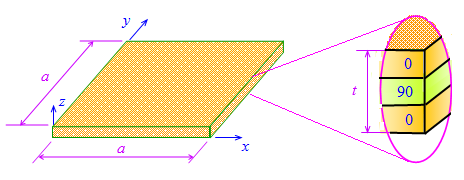
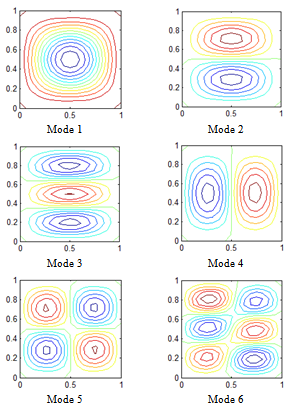
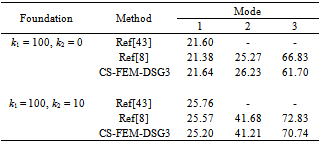
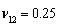 ; G12=0.6E2; a/t = 100. A non-dimensional frequency parameter
; G12=0.6E2; a/t = 100. A non-dimensional frequency parameter 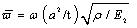 is also used.
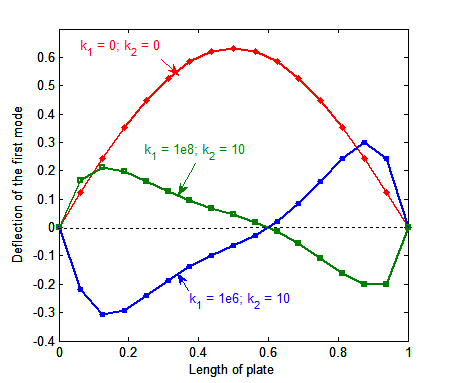
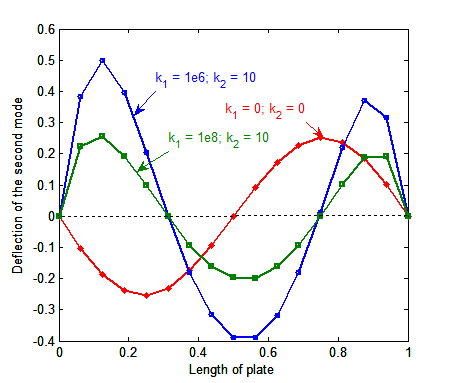
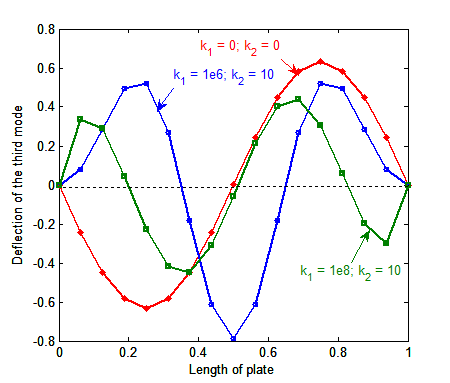
is also used.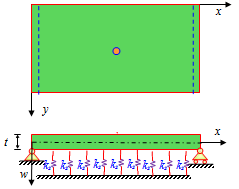
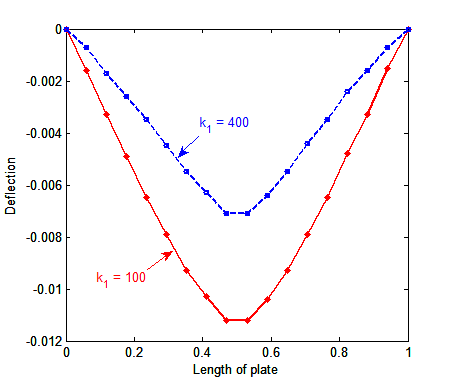
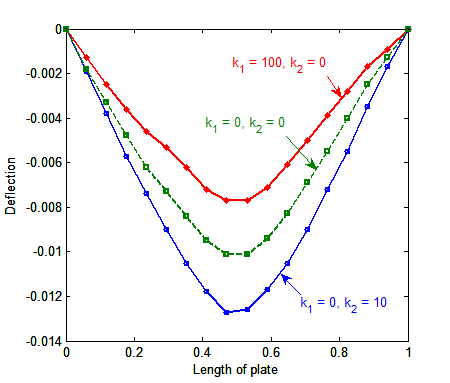
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML