-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2013; 3(6A): 10-18
doi:10.5923/s.cmaterials.201309.02
A Rotation-free Isogeometric Analysis for Composite Sandwich Thin Plates
Chien. H. Thai 1, T. Rabczuk 2, H. Nguyen-Xuan 1, 3
1Division of Computational Mechanics, Ton Duc Thang University HoChiMinh City, Vietnam
2Institute of Structural Mechanics, Bauhaus-University Weimar, Marienstraße 15, Weimar, 99423, Germany
3Department of Mechanics, Faculty of Mathematics & Computer Science, University of Science HoChiMinh City, Vietnam
Correspondence to: T. Rabczuk , Institute of Structural Mechanics, Bauhaus-University Weimar, Marienstraße 15, Weimar, 99423, Germany.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a rotation-free isogeometric formulation for static analysis of composite sandwich plates is presented. The idea relies on a combination of isogeometric analysis with a classical laminate plate theory (CLPT). Isogeometric analysis (IGA) based on non-uniform rational B-spline(NURBS) basic function was recently proposed to preserve exact geometries and to enhance very significantly the accuracy of the traditional finite elements. B-splines basis functions (or NURBS) is used to represent for both geometric and field variable approximations, which provide a flexible way to make refinement and degree elevation. They enable us to achieve easily the smoothness with arbitrary continuity order compared with the traditional FEM. CLPT ignores the transverse shear deformation so it is only applied for thin plates. In our formulation, only deflection variables (without rotational degrees of freedom (dof)) are used for each control point. Essential displacements and rotations boundary conditions can be satisfied strongly by assigning control variable values on the boundary and these adjacent to the boundary, respectively. Several numerical examples are illustrated to demonstrate the performance of the present method in comparison with other published methods.
Keywords: NURBS, Isogeometric analysis, Rotation-free isogeometric formulation, Composite sandwich plates
Cite this paper: Chien. H. Thai , T. Rabczuk , H. Nguyen-Xuan , A Rotation-free Isogeometric Analysis for Composite Sandwich Thin Plates, International Journal of Composite Materials, Vol. 3 No. A, 2013, pp. 10-18. doi: 10.5923/s.cmaterials.201309.02.
Article Outline
1. Introduction
- Sandwich structures have been widely used in various engineering such as aircrafts, aerospace, vehicles, buildings, etc. Sandwich structures are made of three layers (two face sheets and a core) with different materials stacked together to achieve desired properties (e.g. high stiffness and strength-to-weight ratios, long fatigue life, wear resistance, lightweight, etc). For the analysis of sandwich plate, the exact elasticity solution first has been proposed by Pagano[1] to predict accurately of static behavior. Elasticity solution three-dimensional (3D) can become very expensive when the complex structures are modeled. Generally, computational costs are reduced when two-dimensional model is used. Using two-dimensional model, several plate theories using equivalent single layer have been developed to analyze laminated composite sandwich plates. The classical laminate plate theory (CLPT)[3] can only give good results to thin plates because it ignores the transverse shear deformation. The first-order shear deformation theory (FSDT)[2] can be applied for both moderately thick and thin plates. This theory assumes that transverse shear stresses are constant through the thickness and a shear correction factor is needed to take into account the non-linear distribution of shear stresses. To bypass the limitations of the FSDT, the higher-order shear deformation theories (HSDT) have been developed by Kant et al.[2] for the static analysis of composite sandwich plates based on analytical methods (Navier’s solution). Analytical methods have available for benchmark problems. Thanks to advanced numerical approaches such as finite elements[4, 5], smoothed finite elements(SFEM)[6, 7, 8], meshfree methods [9, 10, 11] and extended meshfree methods[12, 13, 14], we can solve effectively more complicated problems in practice. For illustration of this work, finite element analysis for composite sandwich plates is given by Tran et al.[15] based on HSDT. In addition, two-dimensional model based on zigzag theory is also used to calculate the composite sandwich such as: the static analysis of composite sandwich plate with soft-core by Pandit et al.[16], C0 finite element model for the analysis of sandwich laminates with general layup by Singh et al.[17] and an improved C0 finite element model for the analysis of laminated sandwich plate with soft- core by Chalak et al.[19], etc. In the traditional FE method, a discretized geometry obtained through the so-called meshing process is required. This process often leads to geometrical errors even using the higher-order FEM. Also, the communication of the geometry model and the mesh generation during an analysis process that aims to provide the desired accuracy for the solution is always needed and this constitute a time-consuming part in the overall analysis-design process, especially for industrial problems[20]. To overcome this disadvantage, Hughes et al. [20] have recently proposed a NURBS-based isogeometric analysis to bridge the gap between Computer Aided Design (CAD) and Finite Element Analysis (FEA). In contrast to the standard FEM with Lagrange polynomial basis, isogeometric approach utilized more general basis functions such as Non-Uniform Rational B-splines (NURBS) that are common in CAD approaches. Isogeometric analysis is thus very promising because it can directly use CAD data to describe both exact geometry and approximate solution. For structural mechanics, isogeometric analysis has been extensively studied for structural vibrations[21], the Reissner-Mindlin composite plate[24], the composite plate based on HSDT [25], laminated composite layerwise plates [28], the Reissner-Mindlin shell[22] and Kirchhoff-Love shell[23, 27] and further developments[26], etc. The plates are commonly employed in engineering applications as thin plates. So, CLPT is utilized in this paper to reduce computational costs. We focus on NURBS elements using a rotation-free isogeometric formulation for static analysis of composite sandwich plates. The paper is arranged as follows: a brief of the B-spline and NURBS surface is described in section 2. Section 3 describes an isogeometric approximation for composite sandwich plates. Several numerical examples are illustrated in section 4. Finally we close our paper with some concluding remarks.
2. Nurbs-Based Isogeometric Analysis Fundamentals
2.1. Knot Vectors and Basis Functions
- Let be a nondecreasing Ξ={ξ1,ξ2...,ξn+p+1} sequence of parameter values,
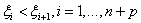 . The
. The 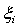 is called knots, and Ξ is the set of coordinates in the parametric space. If all knots are equally spaced the knot vector is called uniform. If the first and the last knots are repeated p + 1 times, the knot vector is described as open. A B-Spline basis function is
is called knots, and Ξ is the set of coordinates in the parametric space. If all knots are equally spaced the knot vector is called uniform. If the first and the last knots are repeated p + 1 times, the knot vector is described as open. A B-Spline basis function is 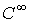 continuous inside a knot span and
continuous inside a knot span and 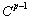 continuous at a single knot. A knot value can appear more than once and is then called a multiple knot. At a knot of multiplicity k the continuity is
continuous at a single knot. A knot value can appear more than once and is then called a multiple knot. At a knot of multiplicity k the continuity is 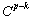 .Given a knot vector, the B-spline basis functions
.Given a knot vector, the B-spline basis functions 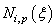 of order p = 0 are defined recursively on the corresponding knot vector as follows
of order p = 0 are defined recursively on the corresponding knot vector as follows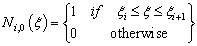 | (1) |
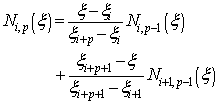 | (2) |
 . In this study, we consider basis functions with
. In this study, we consider basis functions with 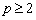 .
.2.2. NURBS Surface
- The B-spline curve is defined as:
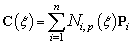 | (3) |
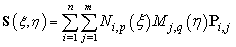 | (4) |
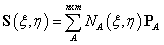 | (5) |
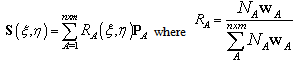 | (6) |
3. A Rotation-Free Isogeometric Formulation for Kirchhoff Plate Model
- Let
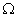 be the domain in R2 occupied by the mid-plane of the plate and u, v and w denote the displacement components in the x, y and z directions, respectively. Using the Kirchhoff model[3], the displacements of any point in the plate can be expressed as
be the domain in R2 occupied by the mid-plane of the plate and u, v and w denote the displacement components in the x, y and z directions, respectively. Using the Kirchhoff model[3], the displacements of any point in the plate can be expressed as 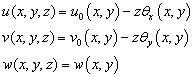 | (7) |
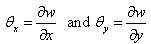 | (8) |
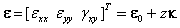 | (9) |
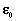 and
and 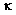 are the in-plane deformations and curvatures of the middle surface, respectively:
are the in-plane deformations and curvatures of the middle surface, respectively: 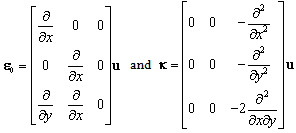 | (10) |
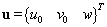 is displacement components at the middle surface.The Hook’s law for an arbitrary layer k, the stress in plane is expressed as
is displacement components at the middle surface.The Hook’s law for an arbitrary layer k, the stress in plane is expressed as 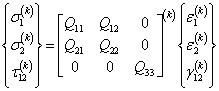 | (11) |
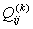 are given by
are given by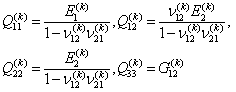 in which
in which 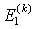 ,
, 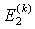 ,
, 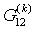 ,
, 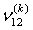 and
and 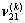 are independent material properties for each layer.The laminate is usually made of several orthotropic layers. Each layer must be transformed into the laminate coordinate system (x, y, z). The stress - strain relationship is given as
are independent material properties for each layer.The laminate is usually made of several orthotropic layers. Each layer must be transformed into the laminate coordinate system (x, y, z). The stress - strain relationship is given as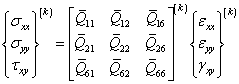 | (12) |
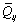 is the transformed material constant matrix[3].A weak form of the static model for composite sandwich plates can be briefly expressed as:
is the transformed material constant matrix[3].A weak form of the static model for composite sandwich plates can be briefly expressed as: 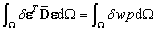 | (13) |
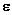 and w are the strains and the deflection and the material matrix
and w are the strains and the deflection and the material matrix 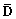 :
: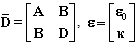 | (14) |
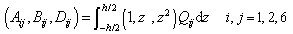 Using the same NURBS basis functions, both the description of the geometry (or the physicalpoint) and the displacement field are expressed as
Using the same NURBS basis functions, both the description of the geometry (or the physicalpoint) and the displacement field are expressed as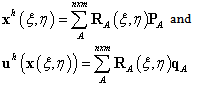 | (15) |
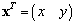 is the physical coordinates vector.
is the physical coordinates vector. 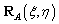 is rational basic functions and
is rational basic functions and 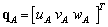 is the degrees of freedom of uh associated to control point A.The strains in Eq. (14) can be expressed to following nodal displacements as:
is the degrees of freedom of uh associated to control point A.The strains in Eq. (14) can be expressed to following nodal displacements as: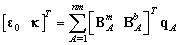 | (16) |
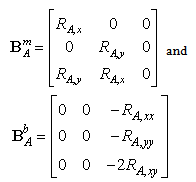 | (17) |
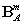 and
and 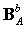 are membrane and bending strain-displacement matrices gained from derivative of shape functions, respectively. The IGA formulation of composite sandwich plates can then be obtained for static analysis:
are membrane and bending strain-displacement matrices gained from derivative of shape functions, respectively. The IGA formulation of composite sandwich plates can then be obtained for static analysis: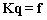 | (18) |
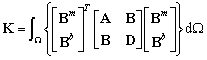 | (19) |
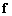 is the global force matrix:
is the global force matrix: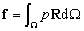 | (20) |
4. Numerical Results
- In this section, several numerical studies using a rotation-free isogeometric analysis are presented. For all numerical examples, quadratic, cubic and quartic NURBS elements integrated with nG = ( p + 1)(q + 1) Gauss points are used . The material parameters are assumed as:Material I: E1 = 25E2; G12 = G13 = 0.5E2; G23 = 0.2E2; v12 = 0.25Material II: Face sheets : E1 = 172.4 GPa; E2= 6.89 GPa; G12 = G13 = 3.45 GPa; G23 = 1.378 GPa; v12 = 0.25 Core: E1 = E2= 0.276 GPa; G12 = 0.1104 GPa; G13 = G23 = 0.414 GPa; v12 = 0.25The normalized displacement and in-plane stresses of composite sandwich plate are defined as:
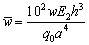 ,
, 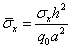 ,
, 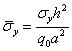 and
and 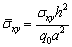 .
.4.1. Three Layer (00/900/00) Square Laminated Plate Under Sinusoidally Distributed Load
- Let us consider a simply supported square laminated plate subjected to a sinusoidal load
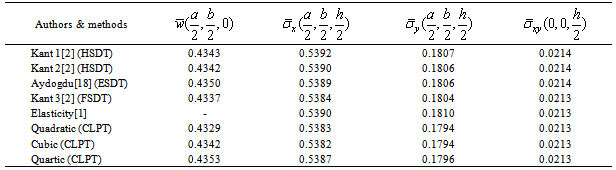
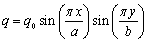 . The length to width ratios is a/b=1 and the length to thickness ratios is a/h=100. Material I described is use. The plate is modeled by 9x9, 13x13, 17x17 and 21x21 B-spline elements. The convergence of normalized displacement and in-plane stresses are given in Figure 1. It can be seen that, the obtained results is very closed with analytical solutions by Kant[2] based on the third shear deformation plate theory and the elasticity solution 3D by Pagano[1]. In order to compare the results, we calculate the normalized displacement and in-plane stresses of the sandwich square plate using 21x21 B-spline elements, as given in Table 1. Obtained results are compared with the several other methods including the close form solution (CFS) based on the exponential shear deformation plate theory (ESDT) by Aydogdu[18], the elasticity solution given in Pagano[1] and analytical solutions based on Navier’s technique by Kant[2]. In[2], there are three-solutions such as: the fully third shear deformation plate theory using 12 dof/node (Kant 1), the third shear deformation plate theory of Reddy using 5 dof/node(Kant 2) and the first shear deformation plate theory 5 dof/node (Kant 3). It is observed that for deflection and stresses the results of the present method agrees well with published results. Figure 2 plots the distribution of stresses through the thickness of the plate. The obtained results are in good agreement with those reported by Kant[2].
. The length to width ratios is a/b=1 and the length to thickness ratios is a/h=100. Material I described is use. The plate is modeled by 9x9, 13x13, 17x17 and 21x21 B-spline elements. The convergence of normalized displacement and in-plane stresses are given in Figure 1. It can be seen that, the obtained results is very closed with analytical solutions by Kant[2] based on the third shear deformation plate theory and the elasticity solution 3D by Pagano[1]. In order to compare the results, we calculate the normalized displacement and in-plane stresses of the sandwich square plate using 21x21 B-spline elements, as given in Table 1. Obtained results are compared with the several other methods including the close form solution (CFS) based on the exponential shear deformation plate theory (ESDT) by Aydogdu[18], the elasticity solution given in Pagano[1] and analytical solutions based on Navier’s technique by Kant[2]. In[2], there are three-solutions such as: the fully third shear deformation plate theory using 12 dof/node (Kant 1), the third shear deformation plate theory of Reddy using 5 dof/node(Kant 2) and the first shear deformation plate theory 5 dof/node (Kant 3). It is observed that for deflection and stresses the results of the present method agrees well with published results. Figure 2 plots the distribution of stresses through the thickness of the plate. The obtained results are in good agreement with those reported by Kant[2].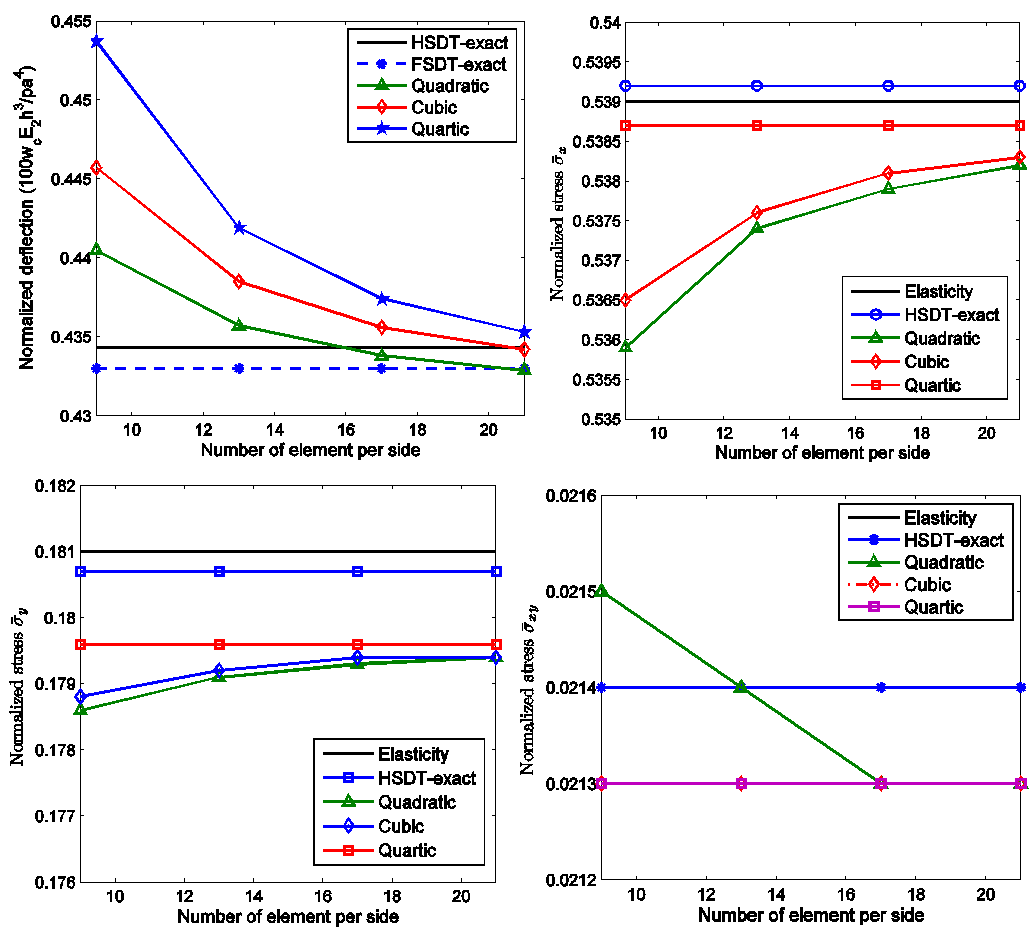 | Figure 1. The in-plane normal and shear stresses of the three-layer composite (00/900/00) simple supported square plates |
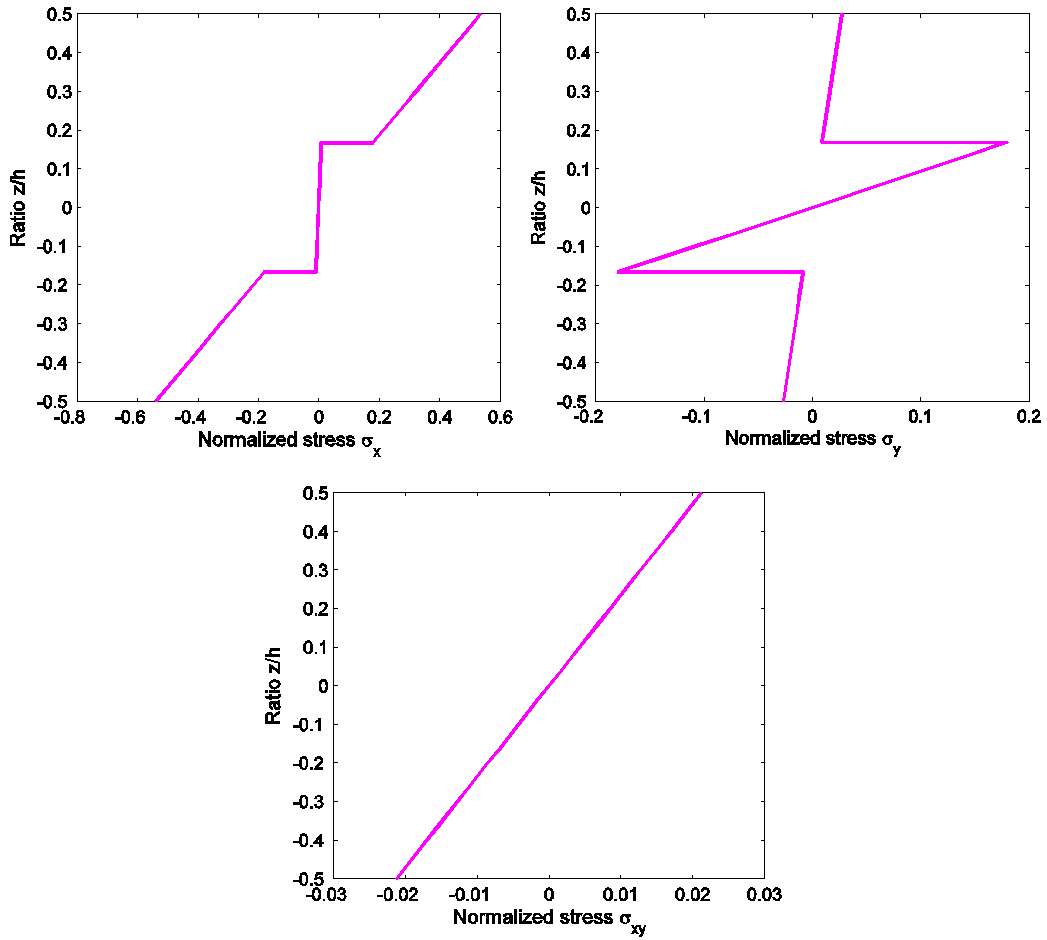 | Figure 2. The in-plane normal and shear stresses of the three-layer composite (00/900/00) simple supported square plates |
|
4.2. The Sandwich (00/core/00) Square Plate under Sinusoidally Distributed Load
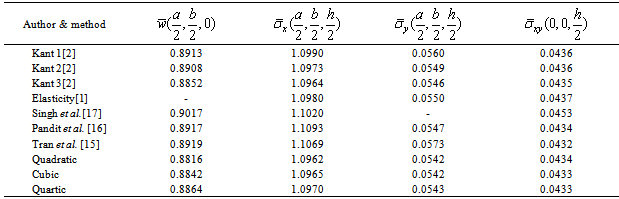
- We consider the sandwich (00/core/00) simply supported square plate subjected to sinusoidally distributed load with the thickness of each face sheet equal h/10. Material II is used. The plate is modeled by 21x21 B-spline element. The normalized transverse displacement and normalized stresses are reported Table 2. The obtained results are compared with the exact elasticity solution by[1], the analytical solution by[2], FEM solutions based on the higher order zigzag plate theory (HOZT) by[16, 17] and and FEM solutions based on the third shear deformation plate theory by[15]. It is found that the results of present method shown good agreements with those solutions. The distribution of stresses through the thickness of the plate is illustrated in Figure 3.
|
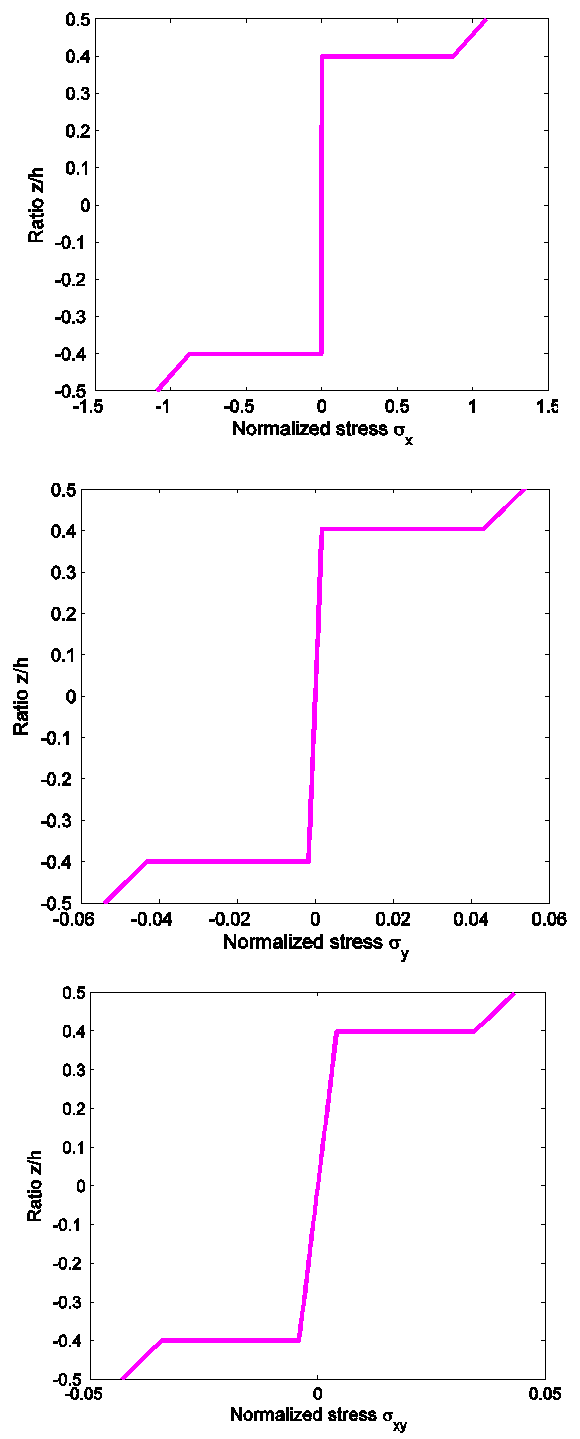 | Figure 3. The in-plane normal and shear stresses of the sandwich (0/core/0) simple supported square plates |
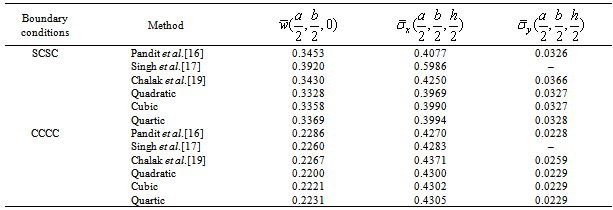
4.3. An-symmetry the Sandwich (00/900/core/00/900) Square Plate under Sinusoidally Load
|
5. Conclusions
- An isogeometric formulation has been developed for static analysis of the composite sandwich plates using a rotation-free isogeometric formulation of CLPT. Weak form of the static model for composite sandwich plates using CLPT was derived. The present method only used three degrees of freedom per node (3 dof/node), and the obtained results are in very good agreement with analytical solution by Kant 1[2] using 12 dof/node, Kant 2[2] using 5 dof/node, FEM solutions using 11 dof/node[16, 17, 19] and FEM solutions using 9 dof/node[15]. The distribution of stresses through the thickness of the sandwich plates are in very good agreement with those of other existing methods.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML