Azam Khalili, Amir Rastegarnia, Bahareh Darvish
Department of Electrical Engineering, Malayer University, Malayer, Iran
Correspondence to: Azam Khalili, Department of Electrical Engineering, Malayer University, Malayer, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The carrier frequency offset (CFO) severely degrades the bit error rate (BER) performance of orthogonal frequency division multiple (OFDM) systems. In this paper, our aim is to develop a robust adaptive CFO estimation algorithm for OFDM system which is able to provide accurate estimate of CFO even in the presence of impulsive noise. To this end, we formulate the CFO estimation in terms of the maximum correntropy criterion (MCC) which is a robust optimality criterion for impulsive noise. Then, we utilize the gradient-ascent method and also apply instantaneous approximation to derive the robust adaptive algorithm. The proposed algorithm has computational complexity similar to the popular least mean-square (LMS), while it is robust against the impulsive signal because of using higher order moments beyond just second order moments. The performance of the proposed algorithm is evaluated under different conditions, including the Gaussian noise, impulsive noise, and time-varying CFO, where simulation results reveal the effectiveness of the proposed algorithm.
Keywords:
Adaptive algorithm, CFO, maximum correntropy criterion, OFDM
Cite this paper: Azam Khalili, Amir Rastegarnia, Bahareh Darvish, A Robust Adaptive Carrier Frequency Offset Estimation Algorithm for OFDM, American Journal of Signal Processing, Vol. 5 No. 2A, 2015, pp. 26-31. doi: 10.5923/s.ajsp.201501.04.
1. Introduction
The orthogonal frequency division multiplexing (OFDM) enables high data rate transmissions in wireless communication systems. It has been chosen as the standards for the European digital and video broadcasting, IEEE802.11a and HIPERLAN/2 [1]. However, the OFDM system is very sensitive to the carrier frequency offset (CFO). CFO is mainly caused by two sources [2]. The first one is the mismatch of carrier frequencies between oscillators in transmitter and receiver, and the other one is due to the Doppler shift, which may change from time to time. Unfortunately CFO destroys the orthogonality among subcarriers, which in turn causes inter-carrier interference (ICI) and degrades the bit error rate (BER) performance severely [2]. This issue motivated the development of CFO estimation algorithms. So far several schemes have been proposed in the literature to estimate the CFO of OFDM systems [3-8]. In [4] a CFO estimation scheme has been developed which uses a training symbol with two identical halves. The given algorithm in [5] utilizes a training symbol with more than two identical halves which increases the estimation range twice that of the scheme in [4]. The algorithm in [6] relies on the maximum-likelihood (ML) criterion and same training symbol as in [5]. A periodogram-based CFO estimation scheme has been proposed in [6], whose estimation range is as large as the bandwidth of the OFDM signal while maintaining the same level of the estimation performance as those of [4, 5]. Most of available works assume CFO as a stationary parameter and do not consider the variation of the offset caused by the Doppler shift. Thus these types of algorithms fail when frequency offset changes from time to time. In [8] an adaptive LMS-based filter has been proposed to estimate CFO, which can track the variation of the offset caused by the Doppler shift. The proposed algorithm in [8] works well under the assumption of the Gaussian distributed noise. However, in many wireless channels, it has been observed that the noise often follows non-Gaussian distribution [9]. Thus, the conventional estimators could suffer from performance degradation in the non-Gaussian noise environments. To address this issue, in this paper our aim is to develop a robust and adaptive algorithm to estimate the CFO which is robust in presence of impulsive noise. To this end we need to go beyond mean squared error to exploit higher order moments of the error. Information theoretic quantities have also been proposed as cost functions in adaptive filters (algorithms). For example a family of Minimum Error Entropy (MEE) based adaptive filters has been proposed [10], [11], wherein the weights are adapted such that the entropy or the information content of the error signal is minimized. Although MEE based algorithm shows robustness in presence of non-Gaussian and impulsive noise, however, it has high computational complexity. The use of Correntropy as a cost function in order to train the filter weights has been proposed in [12]. The given algorithm in [12] which uses maximum correntropy as the cost function has lower computational complexity than MEE, while its robustness is similar to the MEE based algorithm. Thus, in this paper we develop a MCC based adaptive algorithm for CFO estimation. To derive the proposed algorithm, we firstly formulate the CFO estimation according to the MCC, and then we utilize the gradient-ascent method with suitable instantaneous approximations to solve it. We compare the performance of the proposed algorithm with the LMS-based algorithm in [8] in different conditions including the Gaussian noise, impulsive noise, and time varying CFO, where the results show the superior performance of the proposed algorithm.Notation: Through the paper we use lower case bold letters to denote vectors, capital bold letters for matrices. We also use 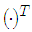 to denote transposition, and
to denote transposition, and 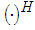 to denote Hermitian transpose. Moreover
to denote Hermitian transpose. Moreover 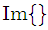 denotes the imaginary part of its argument and
denotes the imaginary part of its argument and 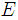 stands for the statistical expectation.The rest of this paper is organized as follows: In section 2, we present some background on CFO estimation problem and also introduce the MCC. The proposed algorithm is presented in section 3. Simulation results are presented in section 4. Section 5 concludes the paper.
stands for the statistical expectation.The rest of this paper is organized as follows: In section 2, we present some background on CFO estimation problem and also introduce the MCC. The proposed algorithm is presented in section 3. Simulation results are presented in section 4. Section 5 concludes the paper.
2. Background
2.1. CFO Estimation Problem
Let us define 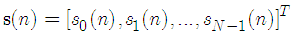 as the nth OFDM data block to be transmitted, where N is the number of subcarriers in the OFDM system. The data are used to modulate orthogonal subcarriers and this modulation can be implemented by inverse discrete Fourier transform (IDFT). Using the matrix representation, the nth block of the modulated signal is [14]
as the nth OFDM data block to be transmitted, where N is the number of subcarriers in the OFDM system. The data are used to modulate orthogonal subcarriers and this modulation can be implemented by inverse discrete Fourier transform (IDFT). Using the matrix representation, the nth block of the modulated signal is [14]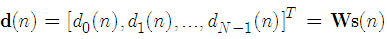 | (1) |
where 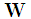 is the
is the 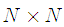 IDFT matrix which is given by
IDFT matrix which is given by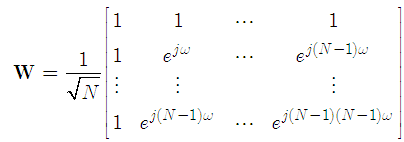 | (2) |
where in (2) 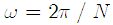 . Then, a cyclic prefix (CP) is inserted where it is assumed that the length of CP is longer than the maximum delay spread of the channel to avoid intersymbol interference (ISI). Finally, the resultant baseband signal is up-converted to the radio frequency (RF) before transmission. At the receiver side, the signal is firstly down-converted and demodulated using discrete Fourier transform (DFT) to recover the desired signal. Without CFO, the received signal can be expressed by
. Then, a cyclic prefix (CP) is inserted where it is assumed that the length of CP is longer than the maximum delay spread of the channel to avoid intersymbol interference (ISI). Finally, the resultant baseband signal is up-converted to the radio frequency (RF) before transmission. At the receiver side, the signal is firstly down-converted and demodulated using discrete Fourier transform (DFT) to recover the desired signal. Without CFO, the received signal can be expressed by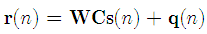 | (3) |
where 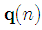 denotes the additive white Gaussian noise (AWGN) and
denotes the additive white Gaussian noise (AWGN) and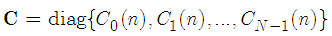 | (4) |
represents the channel characteristics in the frequency domain. In this paper, we assume AWGN channel which means we have 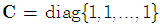 . In the presence of CFO the received signal, after the removal of the CP, is given as
. In the presence of CFO the received signal, after the removal of the CP, is given as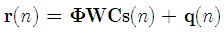 | (5) |
where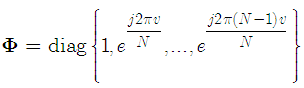 | (6) |
represents the CFO matrix and is the frequency offset normalized to subcarrier spacing. To guarantee the system performance, the CFO must be estimated and compensated before the DFT demodulation. In the presence of the CFO, the received signal, after DFT demodulation, is given by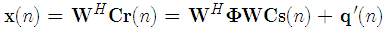 | (7) |
where 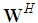 represents the DFT demodulation matrix.
represents the DFT demodulation matrix.
2.2. Maximum Correntropy Criterion
Given two random variable 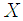 and
and 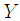 , the correntropy is defined as follows
, the correntropy is defined as follows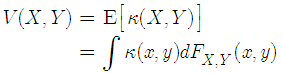 | (8) |
where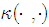 is a shift-invariant Mercer kernel, and
is a shift-invariant Mercer kernel, and 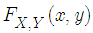 denotes the joint distribution function of
denotes the joint distribution function of 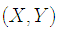 . The Gaussian kernel is the most widely used kernel in correntropy
. The Gaussian kernel is the most widely used kernel in correntropy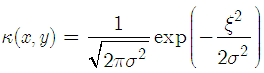 | (9) |
Where 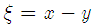 , and
, and  is the kernel width. The maximum correntropy cost function is given by
is the kernel width. The maximum correntropy cost function is given by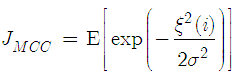 | (10) |
In the sequel, we will use this cost function to derive the proposed algorithm.
3. Proposed CFO Estimation Algorithm
In this section, we present our adaptive CFO estimation algorithm. To this end, let us denote ith sample of recovered signal on subcarrier k as 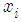 (we ignore the subcarrier index for the sake of simplicity). We also use the training symbols in
(we ignore the subcarrier index for the sake of simplicity). We also use the training symbols in 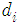 where every
where every 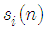 in (2) is a quadrature amplitude modulation (QAM) or phase-shift-keying (PSK) symbol. Then, by comparing the estimation with the training symbols
in (2) is a quadrature amplitude modulation (QAM) or phase-shift-keying (PSK) symbol. Then, by comparing the estimation with the training symbols 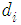 , we define the error signal as
, we define the error signal as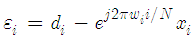 | (11) |
where 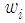 is a real-valued. We now define the cost function in terms of the error signal as
is a real-valued. We now define the cost function in terms of the error signal as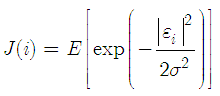 | (12) |
we have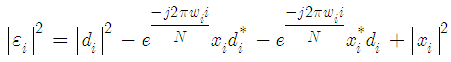 | (13) |
To find the optimum weight that maximizes the cost function in (12), we can use iterative gradient ascent approach as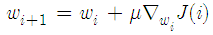 | (14) |
where 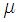 is the step-size parameter and
is the step-size parameter and 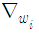 denotes the gradient with respect to
denotes the gradient with respect to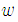 . By computing the gradient
. By computing the gradient 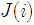 with respect
with respect 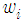 to we obtain
to we obtain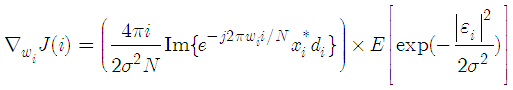 | (15) |
Substituting 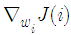 from (15) in (14) gives
from (15) in (14) gives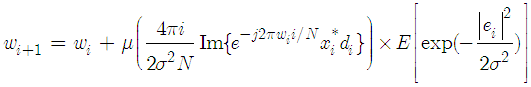 | (16) |
Then, the proposed algorithm can be obtained by replacing the statistical moment in (16) by instantaneous approximation as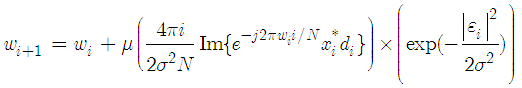 | (17) |
The estimate of CFO is given in terms of 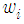 as
as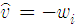 , where the number of iterations equals the number of pilot symbols.
, where the number of iterations equals the number of pilot symbols.
4. Simulation Results
In this section, we evaluate the performance of the proposed algorithm and compare it with the given LMS-based algorithm in [8]. We consider the number of subcarriers in the OFDM system as 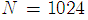 . We consider the mean-square-error (MSE) as the performance metric which is defined as
. We consider the mean-square-error (MSE) as the performance metric which is defined as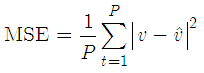 | (18) |
where 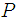 is the number of Monte Carlo runs, which in our simulations was
is the number of Monte Carlo runs, which in our simulations was 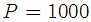 . The CFO is assumed as
. The CFO is assumed as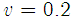 in the following set of simulations. In the first set of simulation we consider Gaussian noise condition where
in the following set of simulations. In the first set of simulation we consider Gaussian noise condition where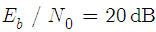 . Fig. 1 shows the learning curves of the proposed algorithm and the LMS-based algorithm for
. Fig. 1 shows the learning curves of the proposed algorithm and the LMS-based algorithm for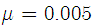 ,
, 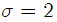 . We can see that the proposed algorithm exhibits a better performance than the algorithm LMS algorithm since it has smaller estimation variance. Fig. 2 presents the MSE versus Eb/N0 for various step-size parameters. It is observed that for both algorithms, the MSE decreases as
. We can see that the proposed algorithm exhibits a better performance than the algorithm LMS algorithm since it has smaller estimation variance. Fig. 2 presents the MSE versus Eb/N0 for various step-size parameters. It is observed that for both algorithms, the MSE decreases as 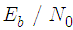 increases or when the step size parameter decreases.
increases or when the step size parameter decreases. 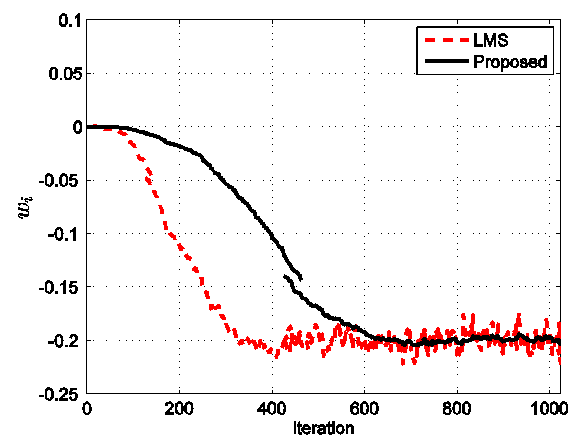 | Figure 1. The learning curves of the proposed algorithm and the LMS-based algorithm for Eb/N0=20 dB |
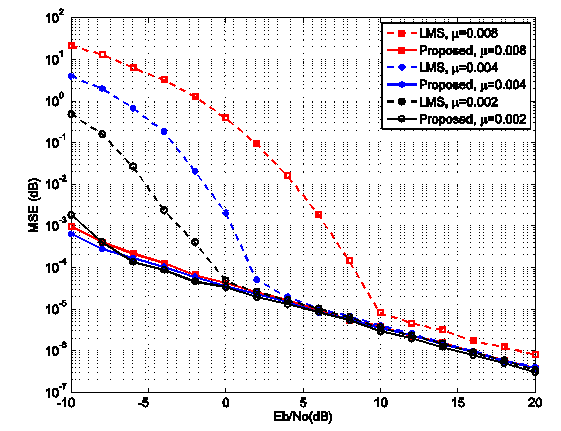 | Figure 2. The MSE performance of both algorithms in terms of the Eb/N0 for different step size parameters |
For small 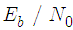 values, the proposed algorithm performs better than the LMS- based algorithm for all step-size values. As
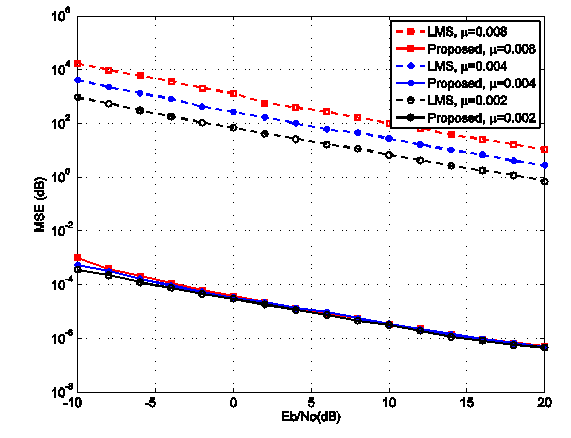
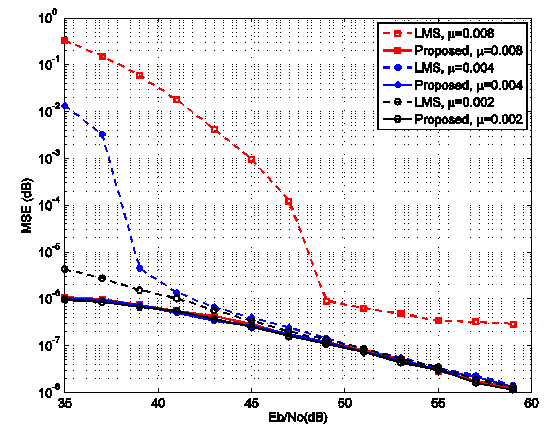
values, the proposed algorithm performs better than the LMS- based algorithm for all step-size values. As 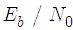 increases, the performance of both algorithms becomes similar, specially for small step-size values.In the next simulation setup, we assume again an OFDM system described above but with impulsive noise. To model the impulsive noise we add a zero-mean complex-valued doubly white Gaussian noise at 0.2dB SNR with probability Pr = 0.03, where Pr denotes the probability that the impulsive noise occurs. The learning curves of the proposed algorithm and the LMS-based algorithm is shown in Fig. 3. The MSE versus Eb/N0 for various step-size parameters indifferent ranges of Eb/N0 are shown in Fig. 4 and Fig. 5. We can see that in the presence of impulsive noise, the performance of LMS-based algorithm decreases, while the proposed algorithm works well in this condition. In Fig. 6, we compare the estimation range of both the proposed LMS-based algorithm and the proposed algorithm under the Gaussian noise and impulsive noise conditions. It is clear that the proposed algorithm has better performance for the whole range of CFO than the LMS-based algorithm.
increases, the performance of both algorithms becomes similar, specially for small step-size values.In the next simulation setup, we assume again an OFDM system described above but with impulsive noise. To model the impulsive noise we add a zero-mean complex-valued doubly white Gaussian noise at 0.2dB SNR with probability Pr = 0.03, where Pr denotes the probability that the impulsive noise occurs. The learning curves of the proposed algorithm and the LMS-based algorithm is shown in Fig. 3. The MSE versus Eb/N0 for various step-size parameters indifferent ranges of Eb/N0 are shown in Fig. 4 and Fig. 5. We can see that in the presence of impulsive noise, the performance of LMS-based algorithm decreases, while the proposed algorithm works well in this condition. In Fig. 6, we compare the estimation range of both the proposed LMS-based algorithm and the proposed algorithm under the Gaussian noise and impulsive noise conditions. It is clear that the proposed algorithm has better performance for the whole range of CFO than the LMS-based algorithm. 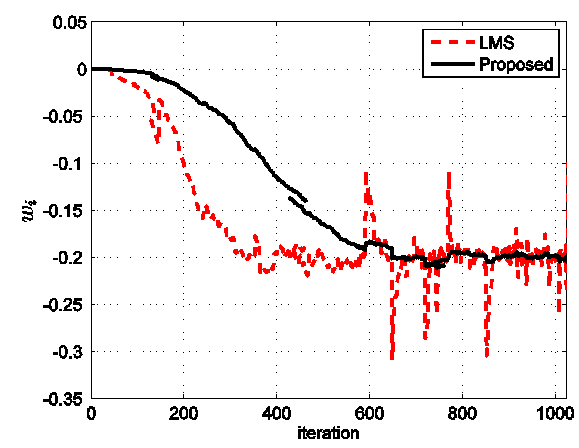 | Figure 3. The MSE performance of both algorithms in terms of the Eb/N0 for different step size parameters |
 | Figure 4. The MSE versus Eb/N0 for various step size parameters under impulsive noise condition |
 | Figure 5. The MSE versus Eb/N0 for various step size parameters under impulsive noise condition |
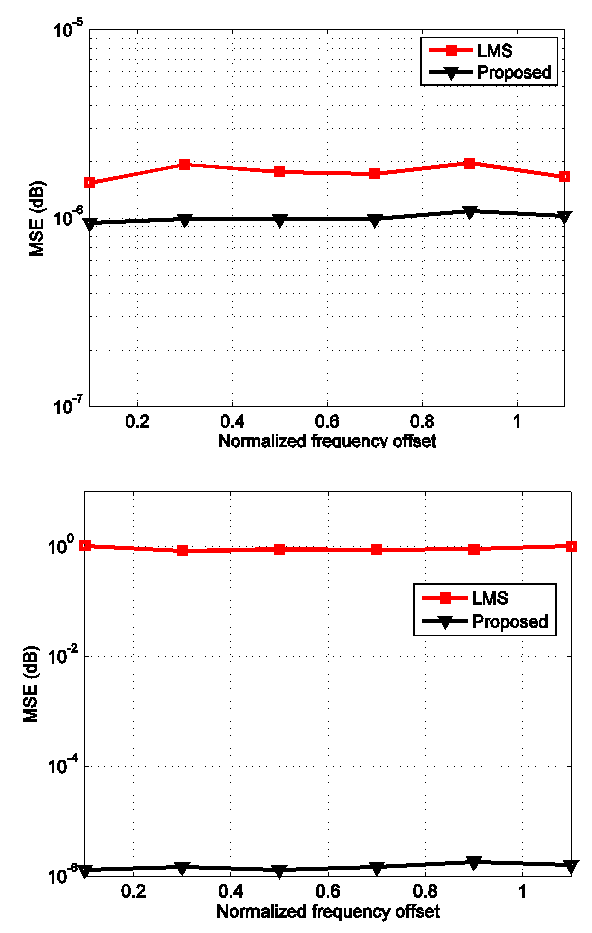 | Figure 6. The estimation range of the proposed LMS-based algorithm and the proposed algorithm under the Gaussian noise (top) and impulsive noise (bottom) conditions |
In Fig. 7, we compare the tracking performance of both algorithms in the presence of impulsive noise. In this case we assume that the normalized frequency offset changes in time according to the following model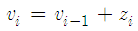 | (19) |
where 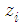 is a zero-mean Gaussian noise with variance 0.005. As we can see the proposed algorithm can track the variation of the CFO and the estimation accuracy is not affected by the impulsive noise
is a zero-mean Gaussian noise with variance 0.005. As we can see the proposed algorithm can track the variation of the CFO and the estimation accuracy is not affected by the impulsive noise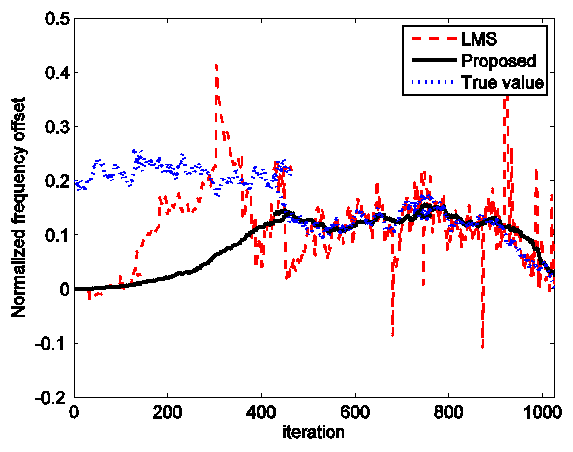 | Figure 7. Tracking performance of both algorithms in the presence of impulsive noise |
5. Conclusions
The carrier frequency offset degrades the performance of OFDM systems. In this paper, we have proposed a correntropy-based adaptive algorithm to estimate the CFO simultaneously in OFDM systems. The proposed algorithm achieves comparable performance and a wider estimation range in comparison with the LMS-based algorithm. The time-varying nature of Doppler shift causes the frequency offset to change from time to time, which affects the estimation accuracy of many existing estimators. The proposed algorithm can track the variation of the Doppler shift well and the estimation accuracy is not affected in the presence of impulsive noise.
References
| [1] | M. Morelli, C.-C. J. Kuo, and M.-O. Pun, Synchronization techniques for orthogonal frequency division multiple access (OFDMA): a tutorial review, Proc. IEEE, 95(7), 1394-1427, July 2007. |
| [2] | T. Pollet, M. Van Bladel, and M. Moeneclaey, BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise, IEEE Trans. Commun., 43(2), 191–193, Feb. 1995. |
| [3] | W. Xu and X. Fu, Blind Frequency Ambiguity Resolution in OFDM Systems Using a Linear Precoder, Wireless Pers Commu, 577-588, 2012. |
| [4] | T. M. Schmidl and D. C. Cox, Robust frequency and timing synchronization for OFDM, IEEE Trans. Commun., 45(12), 1613-1621, Dec. 1997. |
| [5] | S. Chang and E. J. Powers, Efficient frequency-offset estimation in OFDM-based WLAN systems, Electron. Lett., 39(21), 1554-1555, Oct. 2003. |
| [6] | M.-H. Cheng and C.-C. Chou, Maximum-likelihood estimation of frequency and time offsets in OFDM systems with multiple sets of identical data, IEEE Trans. Sig. Process., 54 (7), 2848-2852, July 2006. |
| [7] | G. Ren, Y. Chang, H. Zhang, and H. Zhang, An efficient frequency offset estimation method with a large range for wireless OFDM systems, IEEE Trans. Vehic. Technol., 56(4), 1892-1895, July 2007. |
| [8] | F. Yang, K. H. Li and K. C. Teh, Adaptive LMS-ased algorithm for Carrier Frequency Offset Estimation in OFDM Systems, Proceedings of the 8th International Symposium on Signal Processing and Its Applications, 131–134, 2005. |
| [9] | T. K. Blankenship and T. S. Rappaport, Characteristics of impulsive noise in the 450-MHz band in hospitals and clinics, IEEE Trans. Antennas, Propag., 46(2), 194-203, Feb. 1998. |
| [10] | D. Erdogmus and J. Principe, Generalized information potential criterion for adaptive system training, IEEE Transactions on Neural Networks, 13(5), 1035-1044, September 2002. |
| [11] | D. Erdogmus, Information theoretic learning: Renyi's entropy and its applications to adaptive system training, Ph.D. dissertation, University of Florida, 2002. |
| [12] | A. Singh and J. C. Principe, Using correntropy as a cost function in linear adaptive filters, in Proc. Int. Joint Conf. Neural Networks (IJCNN), 2009, 2950–2955. |
| [13] | B. Chen, L. Xing, J. Liang, N. Zheng, and J. Principe, Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion , IEEE Signal Processing Letters, 21(7), 880–884, July 2014. |
| [14] | F. Yang, K. H. Li, and K. C. Teh, A carrier frequency offset estimator with minimum output variance for OFDM systems, IEEE Commun. Lett., 8, 677–679, Nov. 2004. |

 to denote transposition, and
to denote transposition, and 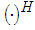 to denote Hermitian transpose. Moreover
to denote Hermitian transpose. Moreover 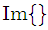 denotes the imaginary part of its argument and
denotes the imaginary part of its argument and 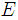 stands for the statistical expectation.The rest of this paper is organized as follows: In section 2, we present some background on CFO estimation problem and also introduce the MCC. The proposed algorithm is presented in section 3. Simulation results are presented in section 4. Section 5 concludes the paper.
stands for the statistical expectation.The rest of this paper is organized as follows: In section 2, we present some background on CFO estimation problem and also introduce the MCC. The proposed algorithm is presented in section 3. Simulation results are presented in section 4. Section 5 concludes the paper.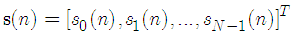 as the nth OFDM data block to be transmitted, where N is the number of subcarriers in the OFDM system. The data are used to modulate orthogonal subcarriers and this modulation can be implemented by inverse discrete Fourier transform (IDFT). Using the matrix representation, the nth block of the modulated signal is [14]
as the nth OFDM data block to be transmitted, where N is the number of subcarriers in the OFDM system. The data are used to modulate orthogonal subcarriers and this modulation can be implemented by inverse discrete Fourier transform (IDFT). Using the matrix representation, the nth block of the modulated signal is [14]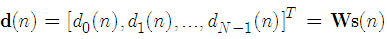
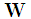 is the
is the  IDFT matrix which is given by
IDFT matrix which is given by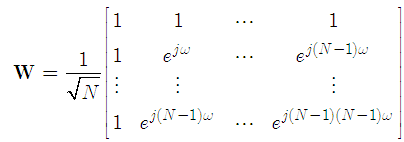
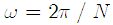 . Then, a cyclic prefix (CP) is inserted where it is assumed that the length of CP is longer than the maximum delay spread of the channel to avoid intersymbol interference (ISI). Finally, the resultant baseband signal is up-converted to the radio frequency (RF) before transmission. At the receiver side, the signal is firstly down-converted and demodulated using discrete Fourier transform (DFT) to recover the desired signal. Without CFO, the received signal can be expressed by
. Then, a cyclic prefix (CP) is inserted where it is assumed that the length of CP is longer than the maximum delay spread of the channel to avoid intersymbol interference (ISI). Finally, the resultant baseband signal is up-converted to the radio frequency (RF) before transmission. At the receiver side, the signal is firstly down-converted and demodulated using discrete Fourier transform (DFT) to recover the desired signal. Without CFO, the received signal can be expressed by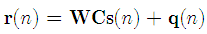
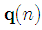 denotes the additive white Gaussian noise (AWGN) and
denotes the additive white Gaussian noise (AWGN) and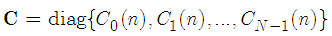
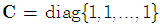 . In the presence of CFO the received signal, after the removal of the CP, is given as
. In the presence of CFO the received signal, after the removal of the CP, is given as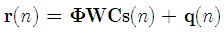
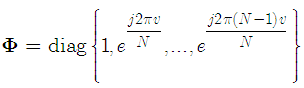
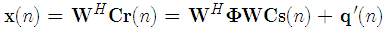
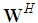 represents the DFT demodulation matrix.
represents the DFT demodulation matrix.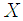 and
and 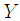 , the correntropy is defined as follows
, the correntropy is defined as follows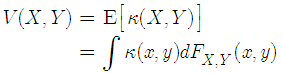
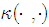 is a shift-invariant Mercer kernel, and
is a shift-invariant Mercer kernel, and 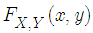 denotes the joint distribution function of
denotes the joint distribution function of 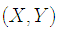 . The Gaussian kernel is the most widely used kernel in correntropy
. The Gaussian kernel is the most widely used kernel in correntropy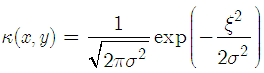
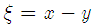 , and
, and  is the kernel width. The maximum correntropy cost function is given by
is the kernel width. The maximum correntropy cost function is given by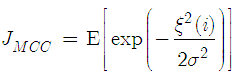
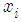 (we ignore the subcarrier index for the sake of simplicity). We also use the training symbols in
(we ignore the subcarrier index for the sake of simplicity). We also use the training symbols in 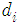 where every
where every 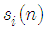 in (2) is a quadrature amplitude modulation (QAM) or phase-shift-keying (PSK) symbol. Then, by comparing the estimation with the training symbols
in (2) is a quadrature amplitude modulation (QAM) or phase-shift-keying (PSK) symbol. Then, by comparing the estimation with the training symbols 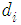 , we define the error signal as
, we define the error signal as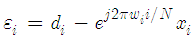
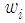 is a real-valued. We now define the cost function in terms of the error signal as
is a real-valued. We now define the cost function in terms of the error signal as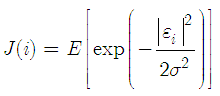
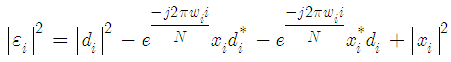
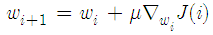
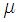 is the step-size parameter and
is the step-size parameter and 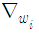 denotes the gradient with respect to
denotes the gradient with respect to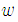 . By computing the gradient
. By computing the gradient 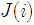 with respect
with respect 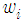 to we obtain
to we obtain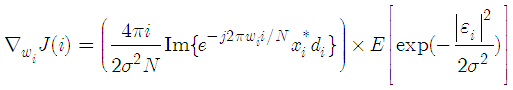
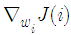 from (15) in (14) gives
from (15) in (14) gives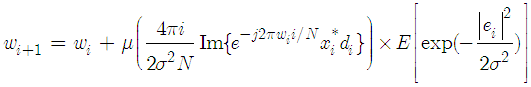
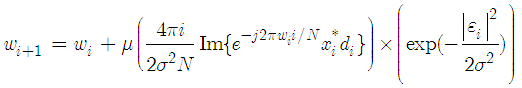
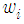 as
as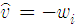 , where the number of iterations equals the number of pilot symbols.
, where the number of iterations equals the number of pilot symbols.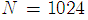 . We consider the mean-square-error (MSE) as the performance metric which is defined as
. We consider the mean-square-error (MSE) as the performance metric which is defined as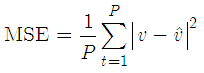
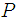 is the number of Monte Carlo runs, which in our simulations was
is the number of Monte Carlo runs, which in our simulations was 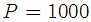 . The CFO is assumed as
. The CFO is assumed as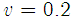 in the following set of simulations. In the first set of simulation we consider Gaussian noise condition where
in the following set of simulations. In the first set of simulation we consider Gaussian noise condition where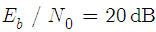 . Fig. 1 shows the learning curves of the proposed algorithm and the LMS-based algorithm for
. Fig. 1 shows the learning curves of the proposed algorithm and the LMS-based algorithm for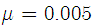 ,
, 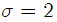 . We can see that the proposed algorithm exhibits a better performance than the algorithm LMS algorithm since it has smaller estimation variance. Fig. 2 presents the MSE versus Eb/N0 for various step-size parameters. It is observed that for both algorithms, the MSE decreases as
. We can see that the proposed algorithm exhibits a better performance than the algorithm LMS algorithm since it has smaller estimation variance. Fig. 2 presents the MSE versus Eb/N0 for various step-size parameters. It is observed that for both algorithms, the MSE decreases as 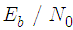 increases or when the step size parameter decreases.
increases or when the step size parameter decreases. 

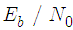 values, the proposed algorithm performs better than the LMS- based algorithm for all step-size values. As
values, the proposed algorithm performs better than the LMS- based algorithm for all step-size values. As 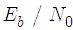 increases, the performance of both algorithms becomes similar, specially for small step-size values.In the next simulation setup, we assume again an OFDM system described above but with impulsive noise. To model the impulsive noise we add a zero-mean complex-valued doubly white Gaussian noise at 0.2dB SNR with probability Pr = 0.03, where Pr denotes the probability that the impulsive noise occurs. The learning curves of the proposed algorithm and the LMS-based algorithm is shown in Fig. 3. The MSE versus Eb/N0 for various step-size parameters indifferent ranges of Eb/N0 are shown in Fig. 4 and Fig. 5. We can see that in the presence of impulsive noise, the performance of LMS-based algorithm decreases, while the proposed algorithm works well in this condition. In Fig. 6, we compare the estimation range of both the proposed LMS-based algorithm and the proposed algorithm under the Gaussian noise and impulsive noise conditions. It is clear that the proposed algorithm has better performance for the whole range of CFO than the LMS-based algorithm.
increases, the performance of both algorithms becomes similar, specially for small step-size values.In the next simulation setup, we assume again an OFDM system described above but with impulsive noise. To model the impulsive noise we add a zero-mean complex-valued doubly white Gaussian noise at 0.2dB SNR with probability Pr = 0.03, where Pr denotes the probability that the impulsive noise occurs. The learning curves of the proposed algorithm and the LMS-based algorithm is shown in Fig. 3. The MSE versus Eb/N0 for various step-size parameters indifferent ranges of Eb/N0 are shown in Fig. 4 and Fig. 5. We can see that in the presence of impulsive noise, the performance of LMS-based algorithm decreases, while the proposed algorithm works well in this condition. In Fig. 6, we compare the estimation range of both the proposed LMS-based algorithm and the proposed algorithm under the Gaussian noise and impulsive noise conditions. It is clear that the proposed algorithm has better performance for the whole range of CFO than the LMS-based algorithm. 



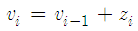
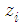 is a zero-mean Gaussian noise with variance 0.005. As we can see the proposed algorithm can track the variation of the CFO and the estimation accuracy is not affected by the impulsive noise
is a zero-mean Gaussian noise with variance 0.005. As we can see the proposed algorithm can track the variation of the CFO and the estimation accuracy is not affected by the impulsive noise
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML