-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2015; 5(2A): 16-25
doi:10.5923/s.ajsp.201501.03
Frequency Estimation of Unbalanced Three-Phase Power Systems Using the Modified Adaptive Filtering
Amir Rastegarnia1, Azam Khalili1, Vahid Vahidpour1, Md Kafiul Islam2
1Department of Electrical Engineering, Malayer University, Malayer, Iran
2Department of Electrical and Computer Engineering, National University of Singapore, Singapore
Correspondence to: Amir Rastegarnia, Department of Electrical Engineering, Malayer University, Malayer, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper, the problem of frequency estimation using adaptive filters is addressed based on the augmented complex normalized least mean squares (ACNLMS) technique. In other words, motivated from ACLMS technique, a new version called ACNLMS that outperforms the previous techniques is proposed. The proposed method makes use of two weight coefficients, like ACLMS, together with normalized time variant step size, thus its promising in increasing and enhancing both convergence rate and accuracy. Then, using derived weight coefficient, the frequency is estimated at each step. The performance and convergence analysis of the proposed method along with simulation results comparing with two existing techniques, CLMS and ACLMS, are provided in critical cases such as various unbalanced conditions and presence of harmonic distortion. Simulation results indicate that the proposed technique achieves a better performance in terms of convergence rate and frequency estimation accuracy as compared with CLMS and ACLMS techniques. Moreover, ACLMS achieves a smaller error variance than the other mentioned cases.
Keywords: Adaptive filter, Frequency estimation, Power systems, Complex signal
Cite this paper: Amir Rastegarnia, Azam Khalili, Vahid Vahidpour, Md Kafiul Islam, Frequency Estimation of Unbalanced Three-Phase Power Systems Using the Modified Adaptive Filtering, American Journal of Signal Processing, Vol. 5 No. 2A, 2015, pp. 16-25. doi: 10.5923/s.ajsp.201501.03.
Article Outline
1. Introduction
- In power networks, knowing the dynamic states of a system is necessary to utilize the system. Since frequency indicates balance/imbalance between load and generation, it has crucial role in a power system. Furthermore, the fact that the amount of active power produced should be always equal to the active power consumed plus losses, is one of the major difficulties in power systems. If the consumed power is more than the produced power, then the frequency would fall and vice versa. Consequently, variations from nominal frequency value indicate lack of balance, such as unexpected abnormal system conditions, between active power consumed plus losses and active power produced. Even small deviations from this value would damage synchronous machines and other applicants. Therefore, making sure of the frequency being constant is of great importance to power system networks. Control and protection of power system require fast and accurate frequency estimation and thus it is a challenging problem that has attracted a lot of attention.Akke [1] considered a test criterion that reflects relevant demands to compare different frequency estimation and detection method. These demands are: speed of convergence, accuracy, and noise rejection. Several frequency estimation techniques have been developed in literature, for example, zero-crossing-based techniques [2], least square error-based adaptive filters (LES) [3], Newton type algorithm [4], discrete Fourier transform (DFT) [5], least mean squares method [6], phase locked loop [7], recursive state estimation-based techniques, and Kalman filters [8], [9]. Among them recursive state estimation-based techniques achieve accurate frequency estimation under critical conditions (unbalanced voltage). Most of these methods, which are based on a single-phase measurement of a system, are limited in terms of system frequency characterization. In a three-phase system, due to existence of six different single-phase voltage signals, no single-phase signal can adequately characterize the system frequency even though line-to-line voltages are considered [10]. Thus, one practical solution is consideration of all three-phase voltages simultaneously, enables unified system frequency estimation as a whole and provides improved robustness.To construct a complex-valued signal from all three-phase voltages, Clark’s αβ transformation is utilized. Among the solutions that have been derived based on Clark transformation, adaptive algorithms are broadly used due to their computational efficiency, simplicity, and robust performance on frequency estimation in the presence of harmonic distortions and noise. Nevertheless, in critical cases under unbalanced voltage conditions, such as when a voltage sag in one or two phases is taking place, standard phase angel calculation techniques utilized in a linear adaptive filter have been proven as suboptimal.In this paper, a modified technique for frequency estimation, which is based on the widely linear complex-valued signal modeling derived from three-phase voltages by Clark transformation under unbalanced conditions, is proposed. It makes use of two weight coefficients, like ACLMS, along with normalized time variant step size to enhance convergence rate and speed using the fact that under unbalanced conditions the complex-valued signal is second order noncircular. To model noncircular signals, not only the standard linear estimation, which is based on covariance matrix of a complex-valued random vector x, i.e., Cxx=E[xxH], is adequate, but the pseudo-covariance matrix Pxx=E[xxT] should also be considered to describe the complete second-order behaviour [11], [12]. In practice, this is accomplished due to widely linear modeling [11], [13], where both x and its complex conjugate x* are combined into augmented input xa=[xT, xH]T. Thus, in order to estimate online frequency of noncircular signals, widely linear modeling-based adaptive filtering method is utilized [14].The remainder of this article is organized as follows. In section 2, we present an overview of CLMS frequency estimation technique Another method called ACLMS [15-19] is also introduced in this section. Wand present our proposed algorithm. In section 3, numerical simulations are presented to illustrate the effectiveness and advantages of the proposed algorithms. Section 4 summarizes the main conclusions of the paper.
2. Frequency Estimation Based on Adaptive Filtering
- The voltages in the power system in a noise free environment can be represented as follows:
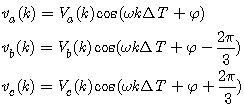 | (1) |
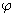 is the phase of fundamental component, and ω=2πf is the angular frequency of the voltage signal, with f being the system frequency. The time-dependent three-phase voltage is transformed by the orthogonal αβ0 transformation matrix [20] into zero-sequence v0 and direct and quadrature axis components, vα and vβ, as Clark’s transform
is the phase of fundamental component, and ω=2πf is the angular frequency of the voltage signal, with f being the system frequency. The time-dependent three-phase voltage is transformed by the orthogonal αβ0 transformation matrix [20] into zero-sequence v0 and direct and quadrature axis components, vα and vβ, as Clark’s transform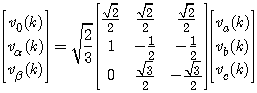 | (2) |
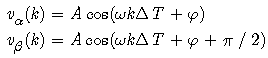 where A is constant amplitude, and vα(k) and vβ(k) are the orthogonal coordinates of a point whose position is time variant at a rate proportional to the system frequency. Only the vα and vβ components are generally utilized in the modeling in practice. Therefore, the complex voltage signal v(k) of the system is given by
where A is constant amplitude, and vα(k) and vβ(k) are the orthogonal coordinates of a point whose position is time variant at a rate proportional to the system frequency. Only the vα and vβ components are generally utilized in the modeling in practice. Therefore, the complex voltage signal v(k) of the system is given by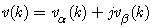 | (3) |
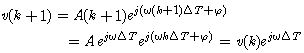 | (4) |
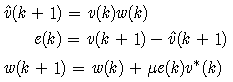 | (5) |
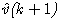 is the estimate of desired signal v(k+1), e(k) is estimation error, and μ is the step size. Comparing (4) and the linear estimation model in (5), the system frequency can be estimated from
is the estimate of desired signal v(k+1), e(k) is estimation error, and μ is the step size. Comparing (4) and the linear estimation model in (5), the system frequency can be estimated from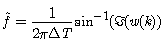 | (6) |
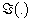 denotes the imaginary part of a complex-valued number.
denotes the imaginary part of a complex-valued number.2.1. Frequency Estimation based on ACLMS Technique
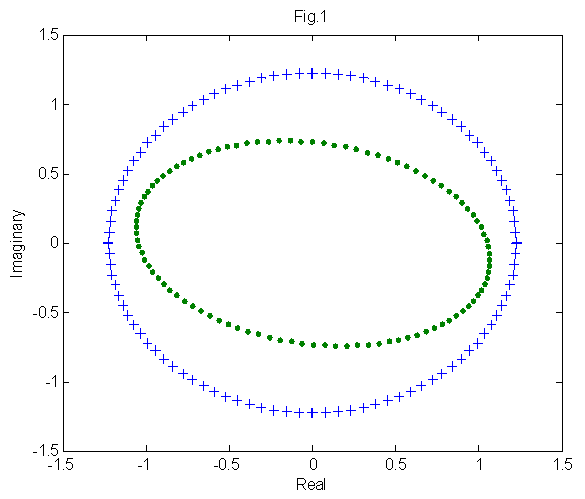
- When three-phase power system deviates from its normal condition, such as, when the voltages of three channels show various levels of transients and dips, voltages Va(k), Vb(k), and Vc(k) are not identical, and samples of v(k) are not located on a constant radius circle, as denoted by ellipse in Fig. 1, lead to breaking down of the v(k) iterative model in (4). In such instance, v(k) has noncircular distribution. From standard three-phase system in (1) and (2), vα(k) and vβ(k) coordinates of complex voltage vα(k) + jvβ(k) is accurately expressed as
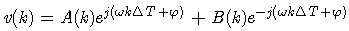 | (7) |
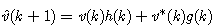 | (8) |
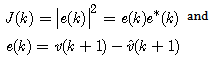 | (9) |
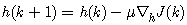 | (10) |
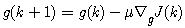 | (11) |
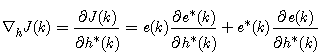 | (12) |
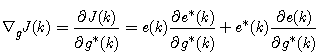 | (13) |
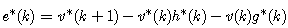 | (14) |
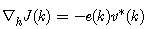 | (15) |
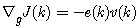 | (16) |
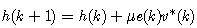 | (17) |
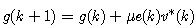 | (18) |
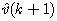 can be give by
can be give by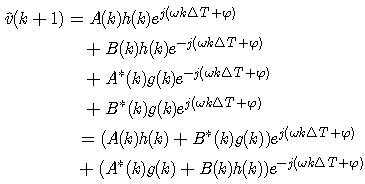 | (19) |
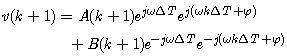 | (20) |
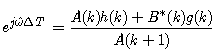 | (21) |
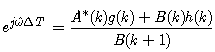 | (22) |
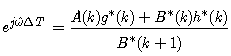 | (23) |
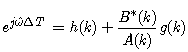 | (24) |
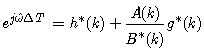 | (25) |
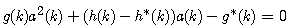 | (26) |
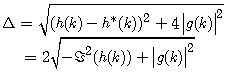 | (27) |
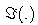 denotes the imaginary part of a complex-valued number. Since a(k)is complex valued, the discriminant is negative, and the two roots can be found as
denotes the imaginary part of a complex-valued number. Since a(k)is complex valued, the discriminant is negative, and the two roots can be found as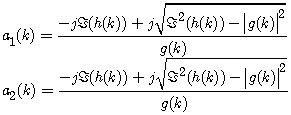 | (28) |
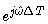 is estimated either by using h(k)+a1(k)g(k) or h(k)+a2(k)g(k). Since the system frequency is far smaller than the sampling frequency, the imaginary part of
is estimated either by using h(k)+a1(k)g(k) or h(k)+a2(k)g(k). Since the system frequency is far smaller than the sampling frequency, the imaginary part of 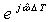 is positive, thus excluding the solution based on a2(k). The system frequency
is positive, thus excluding the solution based on a2(k). The system frequency 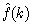 is therefore estimated in the form
is therefore estimated in the form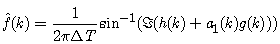 | (29) |
2.2. The Proposed Technique for Frequency Estimation Based on Adaptive Filtering
- In order for frequency estimation of unbalanced three-phase power system to be performed in real-time, the ACLMS technique outperforms the CLMS algorithm. This technique can adapt itself in a successful and satisfactory way in unbalanced conditions and illustrates low sensitivity to three-phase voltage amplitude variations during the time and even in the existence of high-order harmonics. The main disadvantage of ACLMS technique is the speed of convergence. To overcome this, we are motivated to propose a novel technique.Considering the weight coefficients updates h(k) and g(k) of ACLMS algorithm from (17) and (18). The step size μ take constant value. The choice of step size μ is crucial, if not chosen with care; it can destroy the desirable behavior. In many instances, it may be desirable to vary the value of the step size in order to obtain better control over the speed of convergence of the algorithm. Consequently, the bigger the step size, the higher the convergence speed. The updates of both the standard and the conjugate term weight coefficients h(k) and g(k) of ACLMS (proposed algorithm) can be expressed as
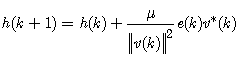 | (30) |
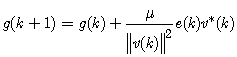 | (31) |
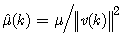 , as opposed to the constant step size, μ, which is used by ACLMS. The performance of ACNLMS is less sensitive in critical state and unbalanced condition than ACLMS.After calculation of weight coefficients h(k) and g(k), the estimated frequency at each step is expressed as
, as opposed to the constant step size, μ, which is used by ACLMS. The performance of ACNLMS is less sensitive in critical state and unbalanced condition than ACLMS.After calculation of weight coefficients h(k) and g(k), the estimated frequency at each step is expressed as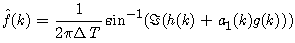 | (32) |
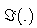 denotes the imaginary part of a complex-valued number, h(k) and g(k) are the standard and conjugate weight coefficients updates respectively, and a1(k) is the acceptable root of the following equation
denotes the imaginary part of a complex-valued number, h(k) and g(k) are the standard and conjugate weight coefficients updates respectively, and a1(k) is the acceptable root of the following equation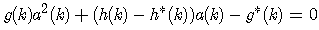 | (33) |
3. Performance Evaluation
- This section is devoted for performance evaluation of the ACNLMS estimator and then examines the tracking abilities of the estimator with respect to several typical power system operating conditions. Capability of proposed technique in (32) in comparison to ACLMS and standard CLMS algorithm in (29) and (6), respectively, is also presented. Simulations were performed in Matlab programming environment with a sampling frequency of 5 kHz and the step size, μ and weight coefficient, w were initialized at 0.001 and 0.998+j0.0634, respectively. Unbalanced three-phase voltages were set according to Va(k)=1.2, Vb(k)=0.7, and Vc(k)=0.3.
3.1. Convergence Speed Comparison of Frequency Estimation under Unbalanced Condition
- In this case study, at t=0.05 s, the unbalanced conditions were imposed to the system. Figure 2 illustrates the tracking performance of the ACNLMS, ACLMS, and CLMS techniques. Both ACNLMS and ACLMS algorithms achieved accurate frequency estimation, however, the convergence speed in ACNLMS technique is faster than ACLMS one.
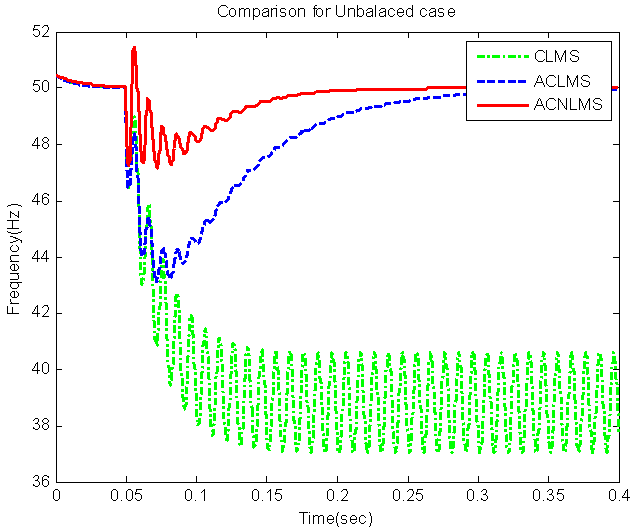 | Figure 2. Comparison of the proposed ACNLMS, ACLMS, and CLMS convergence speed under unbalanced conditions at t=0.05 s |
3.2. Detail Variance Examination of Error Estimation
- In this section, simulations addressed the variance performance of ACNLMS and ACLMS algorithms on frequency estimation of unbalanced system against different levels of noise. The result was obtained by averaging 1000 independent trails. The unbiased property of both ACNLMS and ACLMS estimator can be observed in high SNR region. In Figure 3, the ACNLMS achieved smaller error variance than ACLMS.
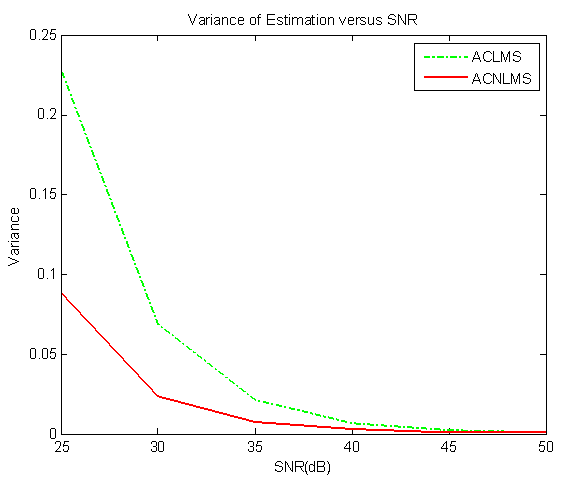 | Figure 3. Comparison of the proposed ACNLMS and ACLMS at different SNRs, obtained by 1000 independent trials |
3.3. The Effect of 100% Single-phase Voltage Sag
- This section shows a 100% single-phase voltage sag suddenly occurred at t=0.05 s in channel c (Vc=0) of the unbalanced three-phase system. The tracking performance in Figure 4 indicates that the CLMS algorithm losts its frequency tracking capability, whereas after convergence, both ACNLMS and ACLMS algorithm were able to accurately track the system frequency, with no oscillations. Once again, the speed of the response of the proposed method is higher than others, such that, at around t=0.15 s, the proposed method converges; whereas, the other algorithms still do not converge.
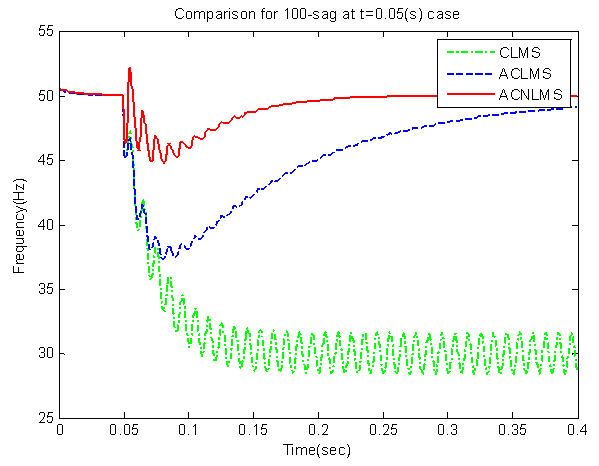 | Figure 4. Frequency estimation by ACNLMS, ACLMS, and CLMS for up to 0.4 s when a 100% single-phase voltage sag occurred in phase channel c (Vc=0) at t=0.05 s |
3.4. The Impact of Oscillatory Variations of Magnitude on the Estimated Frequency
- This set of simulations addressed the impact of oscillatory variations of magnitude on the estimated frequency. In this case study, at t = 0.05 s, the magnitudes of balanced three-phase voltages changed from their normal values. Figure 5 shows that the tracking performance of the proposed ACNLMS algorithm exhibited smaller oscillatory steady-state error than ACLMS algorithm. These small oscillatory steady-state errors of the ACNLMS and ACLMS stems from the assumptions that, at two successive time instants, A(k + 1) ≈ A(k) and B(k +1) ≈ B(k).
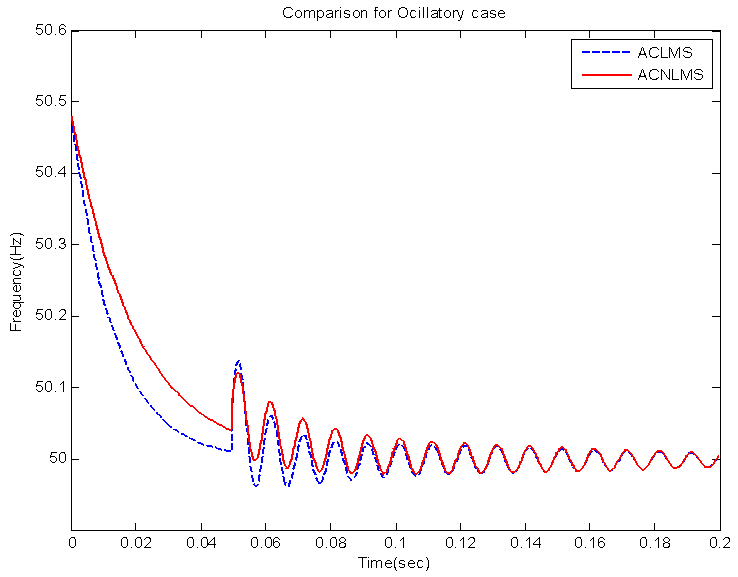 | Figure 5. The impact of oscillatory variations of magnitude on the frequency estimation by ACLMS and ACLMS |
3.5. The Effect of Harmonics on the Performance of Frequency Estimator
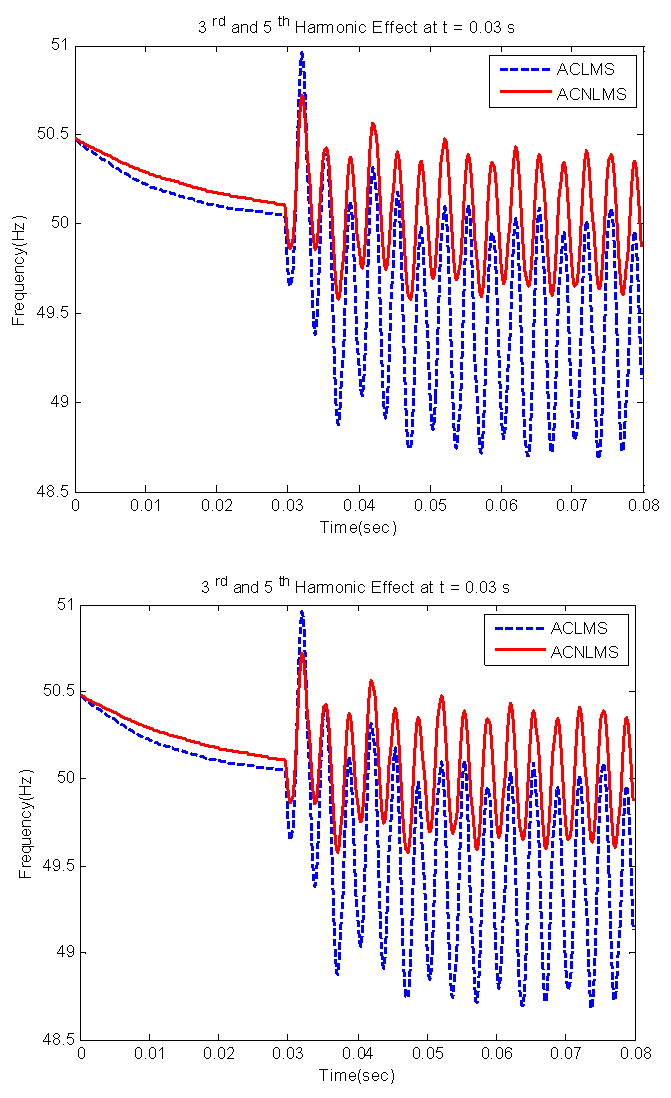
- In this section, effects of harmonic on the performance of the frequency estimator are studied. When the input signal of the estimator is contaminated with harmonics, the estimated frequency is subject to an oscillatory steady-state error and it also deviates from the nominal value by an offset error. In Figure 6(a), a balanced 10% third harmonic and a 5% fifth harmonic of the fundamental frequency were added into the unbalanced three-phase power system at t = 0.03 s. The ACNLMS algorithm achieved better performance with a smaller oscillation error at the steady state as compared with the CLMS algorithm; this advantage was most pronounced when the magnitudes of the third and fifth harmonics varied over a range of (0.0–0.4) p.u., as shown in Figure 6(b).
3.6. The Performance of the Proposed and ACLMS Algorithm for the Case of Frequency Variation
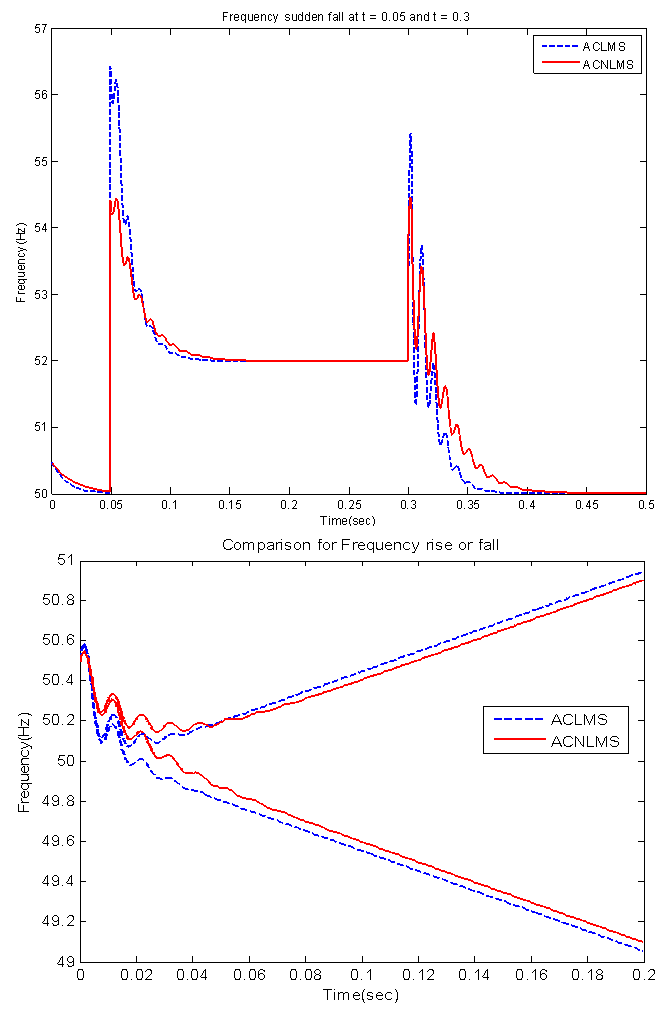
- This section is devoted for performance evaluation of the proposed and ACLMS algorithms for the case of frequency variation. In Figure 7 a balanced voltage signal was affected by the 2-Hz step change in frequency from 50 to 52 Hz at 0.05 s. In this case, both algorithms achieved accurate frequency estimation; however, at t = 0.3 s when the system signal became unbalanced and the frequency was simultaneously changed back to 50 Hz, both ACNLMS and ACLMS algorithms could still track the system frequency with no steady-state error. In Figure 7 (bottom), the 50-Hz fundamental frequency of the unbalanced signal arose and decayed at a rate of 5 Hz/s. The tracking performances of both algorithms are quite similar.
4. Conclusions
- A new method for estimation of frequency under unbalanced condition for three-phase power system is introduced. The method utilizes the newly developed concept of ACLMS which is originally based on the widely linear modeling of the complex-valued signal, derived from three-phase voltages by the Clark transformation. The algorithm was simulated under some unbalanced conditions and exhibited good performance. In contrast to the previous estimator mentioned in literature, the proposed estimator can provide fast and accurate frequency estimate. This paper also compares the proposed technique with standard CLMS and ACLMS techniques. Based on our simulation results, we can conclude that the proposed technique provides robust performance with respect to distortion of the input signal, e.g., harmonics and noise distortions; and also variations of its internal parameter. Moreover, it has the capability to provide fast and accurate frequency estimation under various unbalanced conditions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML