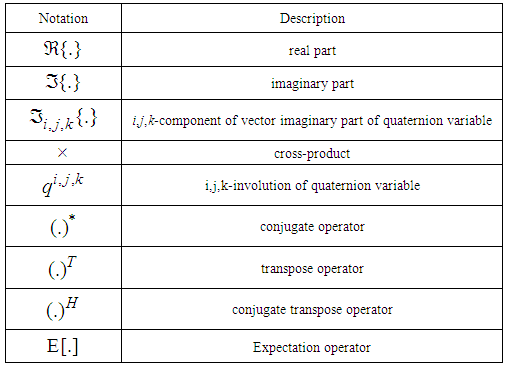
-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2015; 5(2A): 9-15
doi:10.5923/s.ajsp.201501.02
An Adaptive Incremental Algorithm for Distributed Filtering of Hypercomplex Processes
Reza G. Rahmati, Azam Khalili, Amir Rastegarnia, Hossein Mohammadi
Department of Electrical Engineering, Malayer University, Malayer, Iran
Correspondence to: Azam Khalili, Department of Electrical Engineering, Malayer University, Malayer, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
An adaptive network is a collection of agents (nodes) that collaborate with each other through in-network local processing rules in order to perform distributed information processing tasks. In this paper we propose an adaptive incremental network (algorithm) for distributed adaptive filtering of three- and four-dimensional processes. The proposed algorithm exploits spatiotemporal diversity. Moreover, the proposed algorithm employs both the covariance and pseudocovariance terms within its update and can therefore cater for noncircularly symmetric quaternion data. We show that the distributed widely linear (equivalent to augmented term) model outperforms the distributed standard linear model and non-cooperative case. Simulations in the prediction setting on benchmark 4D and 3D signals show the results.
Keywords: Multidimensional adaptive filters, Widely linear model, Quadrivariate processes, Incremental network
Cite this paper: Reza G. Rahmati, Azam Khalili, Amir Rastegarnia, Hossein Mohammadi, An Adaptive Incremental Algorithm for Distributed Filtering of Hypercomplex Processes, American Journal of Signal Processing, Vol. 5 No. 2A, 2015, pp. 9-15. doi: 10.5923/s.ajsp.201501.02.
Article Outline
1. Introduction
- Complex-valued random signals appear in great number of applications such as communications, radar, sonar, geophysics oceanography, optics, and electromagnetic [1]. The complex domain
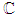 is adequate to process two dimensional signals. A common assumption in complex signal processing is that they are proper or circular. A proper complex random signal is uncorrelated with its complex conjugate, and a circular complex random variable has a probability distribution that is rotationally invariant in the complex plane [2]. Although assumptions are convenient because and simplify many computations, however, there are also many situations where proper and circular signals are very poor models of the underlying physics [3]. To exploit the improper or noncircular nature of complex signals, we need to utilize the complete statistical characterization of complex-valued random signals. For example, to completely extract the second-order information available within the general complex signals we need to consider both the covariance and pseudo-covariance matrices. To access the information contained in this correlation, we can employ widely linear model that take the full second order statistics into account. Widely linear model suitable for processing of general complex signals, both circular and noncircular, is introduced by Picinbono [4]. The augmented representation, i.e.,
is adequate to process two dimensional signals. A common assumption in complex signal processing is that they are proper or circular. A proper complex random signal is uncorrelated with its complex conjugate, and a circular complex random variable has a probability distribution that is rotationally invariant in the complex plane [2]. Although assumptions are convenient because and simplify many computations, however, there are also many situations where proper and circular signals are very poor models of the underlying physics [3]. To exploit the improper or noncircular nature of complex signals, we need to utilize the complete statistical characterization of complex-valued random signals. For example, to completely extract the second-order information available within the general complex signals we need to consider both the covariance and pseudo-covariance matrices. To access the information contained in this correlation, we can employ widely linear model that take the full second order statistics into account. Widely linear model suitable for processing of general complex signals, both circular and noncircular, is introduced by Picinbono [4]. The augmented representation, i.e., 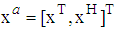 , is required to fully model the second order statistical information within the complex domain, that is,
, is required to fully model the second order statistical information within the complex domain, that is, 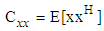 and
and 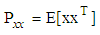 respectively the covariance and pseudo-covariance matrices of complex-valued vector x. Complex-valued adaptive filtering algorithms have been used in a wide range of application. Different complex-valued adaptive filtering algorithms based on the augmented complex statistics have been introduced in the literature [3]. These algorithms are usually termed widely linear or augmented, such as the widely linear LMS (WL-LMS) augmented CLMS (ACLMS) [5,6,7], augmented affine projection (AAPA) [8], widely linear Recursive Least Squares (WL-RLS) algorithms [9], regularized normalized augmented complex LMS (RN-ACLMS) algorithm [10]. To deal with three and four-dimensional processes, Quaternion domain
respectively the covariance and pseudo-covariance matrices of complex-valued vector x. Complex-valued adaptive filtering algorithms have been used in a wide range of application. Different complex-valued adaptive filtering algorithms based on the augmented complex statistics have been introduced in the literature [3]. These algorithms are usually termed widely linear or augmented, such as the widely linear LMS (WL-LMS) augmented CLMS (ACLMS) [5,6,7], augmented affine projection (AAPA) [8], widely linear Recursive Least Squares (WL-RLS) algorithms [9], regularized normalized augmented complex LMS (RN-ACLMS) algorithm [10]. To deal with three and four-dimensional processes, Quaternion domain 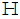 introduces a natural framework for a unified treatment of them. The quaternion algorithms have been developed in the signal processing community, consist of Kalman filtering [11], MUSIC spectrum estimation [12], singular value decomposition for vector sensing [13], and the least-mean-square estimation [14]. The quaternion domain can be significantly used in many multivariate problems based on vector sensors (motion body sensors, seismic, wind modeling). It is therefore natural to extend the so-called augmented complex statistics and widely linear modeling in the complex domain to the quaternion domain. Such widely linear models, include AQLMS [14], widely linear QLMS (WL-QLMS) [15] and WLIQLMS [16]. Distributed information processing tasks appear in many practical applications [17]. There are already several useful strategies for estimation over distributed networks. An example of a distributed method is the consensus strategy [18] in which each node performs a local estimation and fuses its estimate with those of its neighbors so that all nodes converge to the same estimate as the number of iterations increases. The main problem of mentioned methods is that the framework does not allow the network to undertake a continuous learning and optimization which motivated the development of adaptive networks. An adaptive network is a collection of agents (nodes) that collaborate with each other through in-network local processing rules in order to estimate and track parameters of interest [19]. Two major classes of adaptive networks are incremental strategy [20-22] and diffusion strategy [23-25]. In the incremental mode, nodes passing updates to each other in a Hamiltonian cycle in the network, while in diffusion mode, each node can communicate with a subset of neighboring nodes. Adaptive networks based on the widely linear models have been considered in some recent works such as [26-30]. In this paper, we propose an incremental based adaptive network for distributed adaptive filtering of three- and four-dimensional processes, such as those observed in atmospheric modeling (wind, vector fields). The proposed algorithm has the advantage that exploits spatiotemporal diversity to improve the filtering performance. Moreover, it accounts for complex nonlinear dynamics and coupling between the dimensions, which are the main problems of mentioned multidimensional processes. The proposed algorithm employs both the covariance and pseudocovariance terms within its update and can therefore cater for noncircularly symmetric quaternion data. We evaluate the performance of the proposed algorithm with some simulation results.The organization of the paper is as follows: in Section 2 we briefly review the elements of quaternion algebra. In section 3 we derive the proposed algorithm. In section 4 simulations will be presented and finally we conclude our work in section 5. For convenience, a summary of notations is given in Table 1.
introduces a natural framework for a unified treatment of them. The quaternion algorithms have been developed in the signal processing community, consist of Kalman filtering [11], MUSIC spectrum estimation [12], singular value decomposition for vector sensing [13], and the least-mean-square estimation [14]. The quaternion domain can be significantly used in many multivariate problems based on vector sensors (motion body sensors, seismic, wind modeling). It is therefore natural to extend the so-called augmented complex statistics and widely linear modeling in the complex domain to the quaternion domain. Such widely linear models, include AQLMS [14], widely linear QLMS (WL-QLMS) [15] and WLIQLMS [16]. Distributed information processing tasks appear in many practical applications [17]. There are already several useful strategies for estimation over distributed networks. An example of a distributed method is the consensus strategy [18] in which each node performs a local estimation and fuses its estimate with those of its neighbors so that all nodes converge to the same estimate as the number of iterations increases. The main problem of mentioned methods is that the framework does not allow the network to undertake a continuous learning and optimization which motivated the development of adaptive networks. An adaptive network is a collection of agents (nodes) that collaborate with each other through in-network local processing rules in order to estimate and track parameters of interest [19]. Two major classes of adaptive networks are incremental strategy [20-22] and diffusion strategy [23-25]. In the incremental mode, nodes passing updates to each other in a Hamiltonian cycle in the network, while in diffusion mode, each node can communicate with a subset of neighboring nodes. Adaptive networks based on the widely linear models have been considered in some recent works such as [26-30]. In this paper, we propose an incremental based adaptive network for distributed adaptive filtering of three- and four-dimensional processes, such as those observed in atmospheric modeling (wind, vector fields). The proposed algorithm has the advantage that exploits spatiotemporal diversity to improve the filtering performance. Moreover, it accounts for complex nonlinear dynamics and coupling between the dimensions, which are the main problems of mentioned multidimensional processes. The proposed algorithm employs both the covariance and pseudocovariance terms within its update and can therefore cater for noncircularly symmetric quaternion data. We evaluate the performance of the proposed algorithm with some simulation results.The organization of the paper is as follows: in Section 2 we briefly review the elements of quaternion algebra. In section 3 we derive the proposed algorithm. In section 4 simulations will be presented and finally we conclude our work in section 5. For convenience, a summary of notations is given in Table 1.
|
2. Quaternion Domain
- A quaternion variable
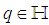 consists of a real part
consists of a real part 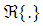 (denoted by subscript
(denoted by subscript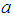 ) and a vector part
) and a vector part 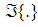 also known as a pure quaternion, consisting of three imaginary components, and can be expressed as
also known as a pure quaternion, consisting of three imaginary components, and can be expressed as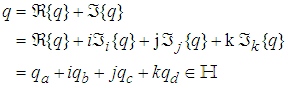 | (1) |
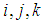 (also known as orthogonal unit vectors) are described as follows
(also known as orthogonal unit vectors) are described as follows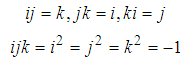 | (2) |
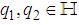 , is defined as
, is defined as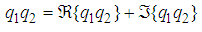 where
where 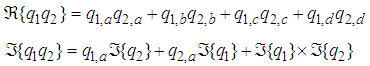 | (3) |
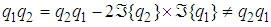 , the noncommutativity of the quaternion multiplication can be observed. The quaternion conjugate is also defined as
, the noncommutativity of the quaternion multiplication can be observed. The quaternion conjugate is also defined as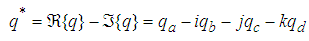 | (4) |
2.1. Quaternion Involutions and Augmented Basis Vector
- In the complex domain
 , elements of a complex number
, elements of a complex number 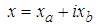 in
in 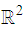 can be described using `augmented' basis vector
can be described using `augmented' basis vector 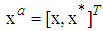 as
as 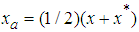 and
and 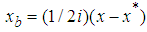 . In the quaternion domain
. In the quaternion domain 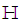 , we seek an `augmented' basis vector to relate its components to those of a quaternion valued variable in
, we seek an `augmented' basis vector to relate its components to those of a quaternion valued variable in 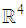 . For this reason, we define three perpendicular quaternion involutions as
. For this reason, we define three perpendicular quaternion involutions as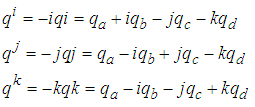 | (5) |
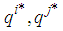 and
and 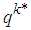 are described as
are described as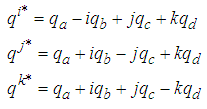 | (6) |
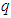 can be computed as
can be computed as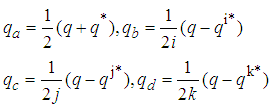 | (7) |
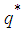 is also an involution, and is given by
is also an involution, and is given by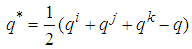 | (8) |
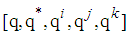 to define an augmented quaternion vector. One augmented basis vector is
to define an augmented quaternion vector. One augmented basis vector is 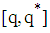 and will be used in this work.
and will be used in this work.2.2. Second Order Circularity in 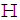 and
and 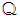 -Properness
-Properness
- For a complex-valued variable
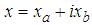 to be second order circular (or
to be second order circular (or 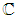 -proper), its probability distribution should be rotation-invariant in complex plane, and therefore have two conditions
-proper), its probability distribution should be rotation-invariant in complex plane, and therefore have two conditions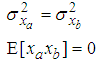 | (9) |
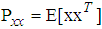 1. Second order circularity is established for a quaternion variable
1. Second order circularity is established for a quaternion variable  when its probability distribution be rotation-invariant with respect to the six pairs of axes:
when its probability distribution be rotation-invariant with respect to the six pairs of axes: 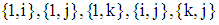 and
and 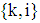 , where ‘1’ denotes the real axis and
, where ‘1’ denotes the real axis and 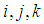 denote the corresponding imaginary axes. In other words, the probability distribution of a
denote the corresponding imaginary axes. In other words, the probability distribution of a  -proper variable is rotation-invariant with respect to all these six pairs of axes. Despite for a
-proper variable is rotation-invariant with respect to all these six pairs of axes. Despite for a 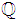 -proper signal, the scalar/real part
-proper signal, the scalar/real part 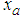 and the vector/imaginary part
and the vector/imaginary part 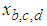 have equal power and are uncorrelated, but the pseudo-covariance
have equal power and are uncorrelated, but the pseudo-covariance 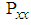 does not vanish, that is,
does not vanish, that is,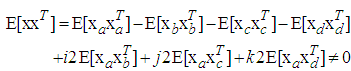 | (10) |
3. I-AQLMS Algorithm
3.1. The Augmented QLMS (AQLMS)
- For the Quaternion LMS, where the output
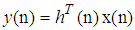 , with
, with 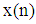 and
and 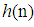 denoting respectively the filter input and the adaptive weight vectors, the update of the adaptive weight vector of QLMS can be obtained as [14]
denoting respectively the filter input and the adaptive weight vectors, the update of the adaptive weight vector of QLMS can be obtained as [14]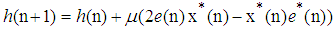 | (11) |
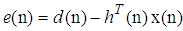 , with
, with 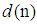 denoting the desired signal. Following the augmented CLMS, augmented CRTRL, and augmented statistics for wind profile [14, 15], we can employ a quaternion-valued widely linear model to cater for both circular and noncircular quaternion processes, given by
denoting the desired signal. Following the augmented CLMS, augmented CRTRL, and augmented statistics for wind profile [14, 15], we can employ a quaternion-valued widely linear model to cater for both circular and noncircular quaternion processes, given by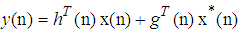 | (12) |
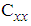 and pseudocovariance
and pseudocovariance 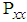 . Similarly to update for vector
. Similarly to update for vector  , that for vectorin (12) can be obtained as follows
, that for vectorin (12) can be obtained as follows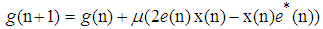 | (13) |
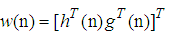 | (14) |
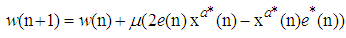 | (15) |
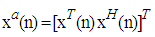 and error
and error 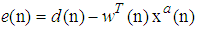 .
.3.2. Derivation of I-AQLMS Algorithm
- Consider a network with N distributed nodes over an area, as shown in Figure 3. Each node
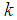 has access to local measurement
has access to local measurement 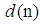 and a regressor vector
and a regressor vector 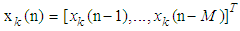 , at time instant n. the flow of data in a sequential manner from one node to the adjacent node by an incremental protocol can be described as follows: assume that
, at time instant n. the flow of data in a sequential manner from one node to the adjacent node by an incremental protocol can be described as follows: assume that 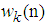 denotes the local estimate of optimum weight vector
denotes the local estimate of optimum weight vector 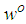 at node
at node 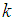 at time n, and node
at time n, and node 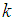 has access to local estimate
has access to local estimate 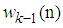 at previous node
at previous node 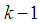 in the defined cycle. by starting with the initial condition
in the defined cycle. by starting with the initial condition 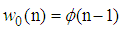 in node 1, and going across the network, then at the end of cycle, the local estimate at node N,
in node 1, and going across the network, then at the end of cycle, the local estimate at node N, 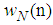 , will be considered as
, will be considered as 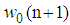 for next iteration. This algorithm for AQLMS is summarized in Table 2, where
for next iteration. This algorithm for AQLMS is summarized in Table 2, where 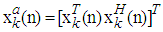 and
and 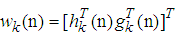 .
.
|
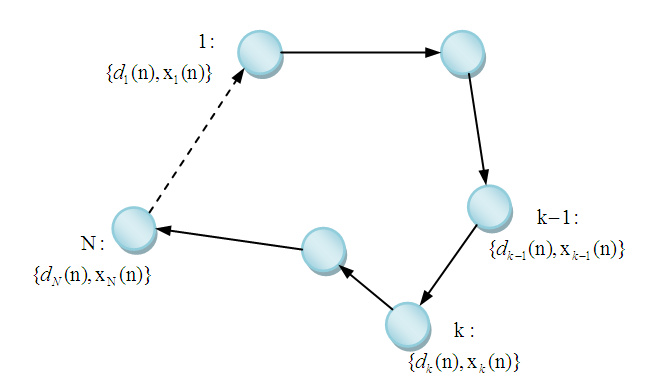 | Figure 1. Incremental mode of cooperation structure |
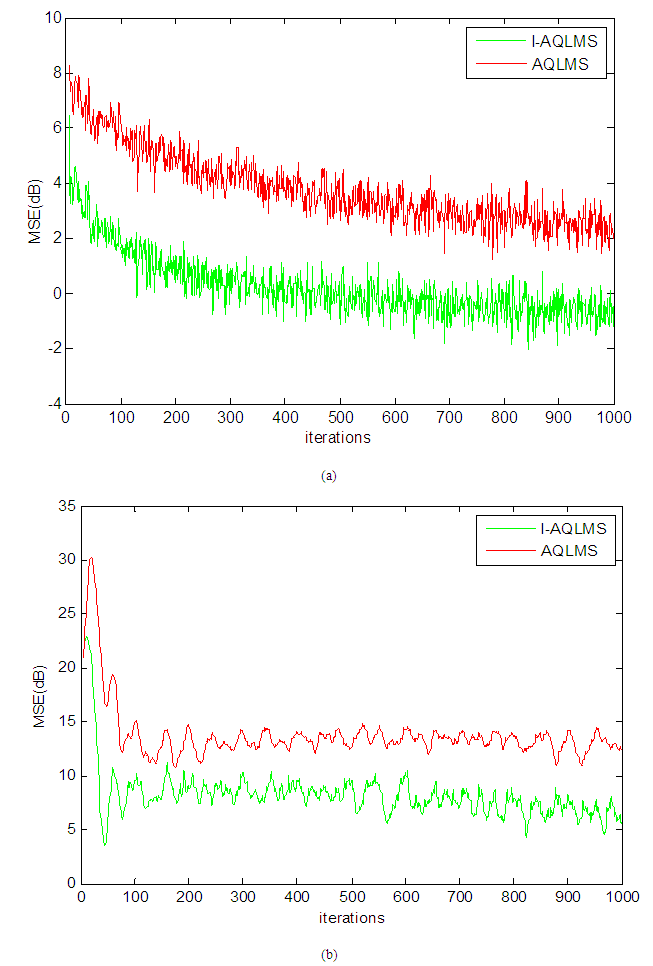 | Figure 2. Comparison of MSEs of non-cooperative AQLMS and Incremental AQLMS algorithms for prediction of (a) circular 4D AR(4) process with 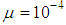 , and (b) noncircular 3D Lorenz signal with , and (b) noncircular 3D Lorenz signal with 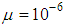 |
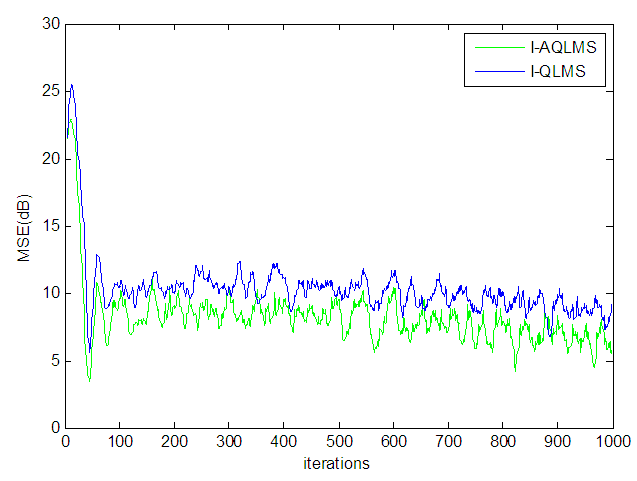 | Figure 3. Comparison of MSEs of I-AQLMS and I-QLMS algorithms for prediction of noncircular 3D Lorenz signal with 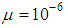 |
4. Simulation
- The one step ahead prediction performance of proposed algorithms I-AQLMS is compared with its standard linear counterpart (I-QLMS) and non-cooperative case. The network consist of N = 10 nodes, and filter order is set to M = 5. For evaluating the algorithms performance, we employ two signals, one is a three-dimensional nonlinear system known as the Lorenz attractor used originally to model atmospheric turbulence, but also to model lasers, dynamos, and the motion of waterwheel [5]. Mathematically, the Lorenz system can be expressed as a system of coupled differential equations:
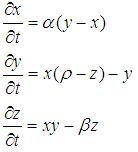 | (16) |
 , and the other signal is generated by a linear AR(4) model as follows
, and the other signal is generated by a linear AR(4) model as follows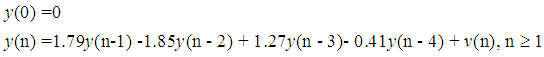 | (17) |
5. Conclusions
- We have proposed an Incremental Augmented QLMS (I-AQLMS) algorithm for processing of both circular and noncircular quaternion-valued signals collaboratively. The advantage of the widely linear incremental algorithm over standard linear incremental and noncooperative case in terms of convergence speed and steady state performance has been shown in simulations on synthetic signals.
Note
- 1. For a
 -proper signal, the pseudo-covariance
-proper signal, the pseudo-covariance 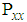 vanishes, that is,
vanishes, that is, 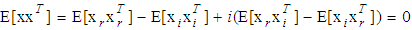 , this is because for a
, this is because for a  -proper signal, the real part
-proper signal, the real part 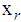 and the imaginary part
and the imaginary part 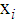 have the same power and are uncorrelated.
have the same power and are uncorrelated. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML