-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2015; 5(2A): 1-8
doi:10.5923/s.ajsp.201501.01
An Adaptive Diffusion Algorithm Based on Augmented QLMS for Distributed Filtering of Hypercomplex Processes
Azam Khalili, Reza G. Rahmati, Amir Rastegarnia
Department of Electrical Engineering, Malayer University, Malayer, Iran
Correspondence to: Azam Khalili, Department of Electrical Engineering, Malayer University, Malayer, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
An adaptive network consists of a set of adaptive filters that cooperate with each other to solve an optimization problem using a predefined cost function. In this paper we propose an adaptive diffusion algorithm based on augmented quaternion least mean square (AQLMS) for processing of three and four-dimensional processes collaboratively. We provide mean stability of proposed algorithm and show that the distributed widely linear (equivalent to augmented term) model outperforms the distributed standard linear model and non-cooperative case. Simulations in the prediction setting on benchmark 4D and 3D signals show the results.
Keywords:
Multidimensional adaptive filters,  -properness, Widely linear model, Quadrivariate processes, Cooperation, Prediction, Diffusion, Adaptive network
-properness, Widely linear model, Quadrivariate processes, Cooperation, Prediction, Diffusion, Adaptive network
Cite this paper: Azam Khalili, Reza G. Rahmati, Amir Rastegarnia, An Adaptive Diffusion Algorithm Based on Augmented QLMS for Distributed Filtering of Hypercomplex Processes, American Journal of Signal Processing, Vol. 5 No. 2A, 2015, pp. 1-8. doi: 10.5923/s.ajsp.201501.01.
Article Outline
1. Introduction
- Network is the science related to issues such as assemblage, processing, cooperation, and distribution information over graphs connecting a multitude of nodes, in which collaboration among nodes can result in superior adaptation and learning performance over graphs [1]. The applications include the areas of intrusion detection, spectrum sensing, online dictionary learning, sparse data recovery, target localization, and biological networks. In the first scenario, each node acquires data and processes it independently of the other nodes. We refer to this mode of processing as noncooperative mode. In the second scenario, the nodes transmit their own data to a fusion center for processing. We refer to this mode of processing as centralized or batch mode. although centralized solution is powerful, but it suffers from a number of drawbacks such as fusion center failures and communication burden between the nodes and the fusion center.There are several distributed strategies to solve these problems that are based on incremental (e.g., [2-6]), consensus (e.g., [7-9]), and diffusion (e.g., [10-14]) techniques. although the incremental method requires low communication traffic between nodes with each node receiving data from one preceding node and sharing data with one subsequent node, but this mode of cooperation suffers from a number of limitation such as node and link failures, whilst determining a cyclic path that visits all nodes is generally an NP-hard problem. We can motivate two other distributed techniques based on consensus and diffusion strategies that do not suffer from these limitations. Despite its high communication in analogy to incremental strategy, diffusion strategy has robustness to link and node failures.A superior result in augmented complex statistics is the work by Neeser and Massey [15], who have devised a comprehensive description of the concept of properness (second order circularity) and rotation invariant probability distribution for processing of the complex-valued (two dimensional) signals. They showed that the covariance matrix
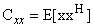 of a complex random vector x alone is not adequate to describe second order statistical information completely for general complex-valued signals and thus the pseudocovariance or complementary covariance matrix
of a complex random vector x alone is not adequate to describe second order statistical information completely for general complex-valued signals and thus the pseudocovariance or complementary covariance matrix 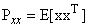 also needs to be taken into account. These fundamentals have been successfully used to design widely linear algorithms for processing of the improper complex-valued signals optimally in adaptive signal processing [16], that is, for an optimal linear estimator, the 'augmented' input
also needs to be taken into account. These fundamentals have been successfully used to design widely linear algorithms for processing of the improper complex-valued signals optimally in adaptive signal processing [16], that is, for an optimal linear estimator, the 'augmented' input 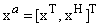 must be used, leading to the widely linear model given by
must be used, leading to the widely linear model given by 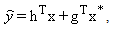 with h and g denoting filter coefficients.In order to deal with three and four dimensional signals (such as bodysensor measurements [17], color images [18], wind and renewable energy [19]), Quaternion domain
with h and g denoting filter coefficients.In order to deal with three and four dimensional signals (such as bodysensor measurements [17], color images [18], wind and renewable energy [19]), Quaternion domain  is introduced and can be regarded as a non-commutative extension of complex domain
is introduced and can be regarded as a non-commutative extension of complex domain  [20]. It is therefore natural to extend the developments in so-called augmented complex statistics and widely linear modeling in the complex domain to the quaternion domain, in order to provide enhanced accuracy especially for processes with of different powers in data channels, such as in wind modeling. Some of adaptive filtering algorithms introduced in quaternion domain include widely linear quaternion least mean square (WLQLMS) [21], widely linear involution quaternion LMS (WLIQLMS) [22], augmented QLMS (AQLMS) [23]. Adaptive networks based on the widely linear models have been considered in some recent works such as [24-28]. In this paper, we propose a diffusion based adaptive network for distributed adaptive filtering of three- and four-dimensional processes, such as those observed in atmospheric modeling (wind, vector fields). The proposed algorithm has the advantage that exploits spatiotemporal diversity to improve the filtering performance. Moreover, it accounts for complex nonlinear dynamics and coupling between the dimensions, which are the main problems of mentioned multidimensional processes. The proposed algorithm employs both the covariance and pseudocovariance terms within its update and can therefore cater for noncircularly symmetric quaternion data. We derive the required condition for mean stability of the proposed algorithm. We evaluate the performance of the proposed algorithm with some simulation results, where the results show the superior performance of the proposed algorithm.The organization of this paper is as follows: in section 2, we introduce the quaternion domain. In section 3, we derive the proposed distributed algorithm. In section 4, we analyze the mean stability of proposed algorithm. In section 5, the simulations will be presented and finally in section 6, we conclude our work.A summary of notations is given in Table 1.
[20]. It is therefore natural to extend the developments in so-called augmented complex statistics and widely linear modeling in the complex domain to the quaternion domain, in order to provide enhanced accuracy especially for processes with of different powers in data channels, such as in wind modeling. Some of adaptive filtering algorithms introduced in quaternion domain include widely linear quaternion least mean square (WLQLMS) [21], widely linear involution quaternion LMS (WLIQLMS) [22], augmented QLMS (AQLMS) [23]. Adaptive networks based on the widely linear models have been considered in some recent works such as [24-28]. In this paper, we propose a diffusion based adaptive network for distributed adaptive filtering of three- and four-dimensional processes, such as those observed in atmospheric modeling (wind, vector fields). The proposed algorithm has the advantage that exploits spatiotemporal diversity to improve the filtering performance. Moreover, it accounts for complex nonlinear dynamics and coupling between the dimensions, which are the main problems of mentioned multidimensional processes. The proposed algorithm employs both the covariance and pseudocovariance terms within its update and can therefore cater for noncircularly symmetric quaternion data. We derive the required condition for mean stability of the proposed algorithm. We evaluate the performance of the proposed algorithm with some simulation results, where the results show the superior performance of the proposed algorithm.The organization of this paper is as follows: in section 2, we introduce the quaternion domain. In section 3, we derive the proposed distributed algorithm. In section 4, we analyze the mean stability of proposed algorithm. In section 5, the simulations will be presented and finally in section 6, we conclude our work.A summary of notations is given in Table 1.
|
2. Quaternion Domain
- The quaternion domain is a non-commutative extension of the complex domain, and devises an adequate framework to process three and four-dimensional signals. A quaternion variable
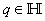 constitutes a real part
constitutes a real part 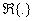 and a vector part
and a vector part 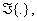 also known as a pure quaternion, consisting of three imaginary components, and can be expressed as
also known as a pure quaternion, consisting of three imaginary components, and can be expressed as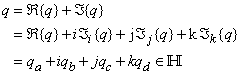 | (1) |
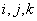 are related as follows
are related as follows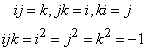 | (2) |
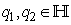 , the noncommutativity property of the quaternion product is described as follows
, the noncommutativity property of the quaternion product is described as follows with
with 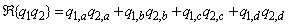
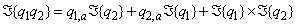 | (3) |
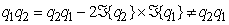 , with symbol
, with symbol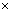 denoting the vector product. The quaternion conjugate is also defined as
denoting the vector product. The quaternion conjugate is also defined as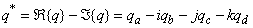 | (4) |
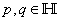 , It follows that
, It follows that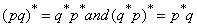 | (5) |
2.1. Augmented Basis Vector
- The real and imaginary parts of a complex variable
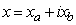 can be extracted as
can be extracted as 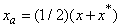 and
and 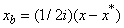 . It is therefore natural to consider ‘augmented’ basis vector as
. It is therefore natural to consider ‘augmented’ basis vector as 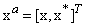 to describe the elements of the corresponding bivariate signal in
to describe the elements of the corresponding bivariate signal in 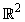 . In order to employ such manipulation in the quaternion domain, three perpendicular quaternion involutions (self-inverse mappings) is defined as follows
. In order to employ such manipulation in the quaternion domain, three perpendicular quaternion involutions (self-inverse mappings) is defined as follows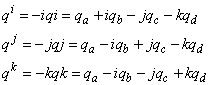 | (6) |
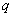 can now be expressed as [29]
can now be expressed as [29]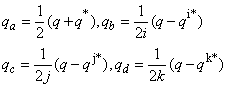 | (7) |
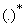 is also an involution, and is expressed as
is also an involution, and is expressed as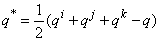 | (8) |
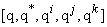 to define an augmented quaternion vector in quaternion domain
to define an augmented quaternion vector in quaternion domain  to relate the components of quaternion signal to its real valued quadrivariate counterpart in
to relate the components of quaternion signal to its real valued quadrivariate counterpart in  . In this paper, we use the vector
. In this paper, we use the vector 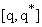 as augmented basis vector for widely linear modeling.
as augmented basis vector for widely linear modeling.2.2. Second Order Circularity in  and
and  -Properness
-Properness
- Second order circularity is established for a quaternion variable
 when its probability distribution be rotation-invariant with respect to the six pairs of axes:
when its probability distribution be rotation-invariant with respect to the six pairs of axes: 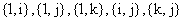 and
and  , with ‘1’ denoting the real axis and
, with ‘1’ denoting the real axis and  the corresponding imaginary axes. In other words, for a quaternion random variable to be
the corresponding imaginary axes. In other words, for a quaternion random variable to be  -proper, it should satisfy the properties summarised in Table 2 [30].
-proper, it should satisfy the properties summarised in Table 2 [30].
|
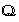 -proper random variables. Finally, the fourth property P4 denotes that the covariance of a quaternion random variable is a sum of the covariances of the variable components.
-proper random variables. Finally, the fourth property P4 denotes that the covariance of a quaternion random variable is a sum of the covariances of the variable components.3. Derivation of D-AQLMS Algorithm
- In order to cater for both circular and noncircular quaternion processes, a quaternion-valued widely linear model based on the augmented basis vector as
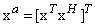 is introduced in [23] and is given by
is introduced in [23] and is given by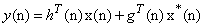 | (9) |
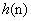 and
and 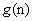 into the compact form
into the compact form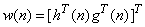 and regarding the non-commutativity of the quaternion products, weight update of the Augmented QLMS (AQLMS) is then given by
and regarding the non-commutativity of the quaternion products, weight update of the Augmented QLMS (AQLMS) is then given by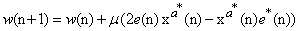 | (10) |
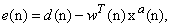 with
with 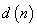 denoting the desired response. In order to investigate this learning algorithm in a distributed manner by diffusion strategy, consider a network with N distributed nodes (as Figure 1) with each node k equipped with an AQLMS filter which has access the realizations
denoting the desired response. In order to investigate this learning algorithm in a distributed manner by diffusion strategy, consider a network with N distributed nodes (as Figure 1) with each node k equipped with an AQLMS filter which has access the realizations 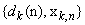 at time n. we denote the desired signal by
at time n. we denote the desired signal by 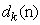 and input regressor vector with length M by
and input regressor vector with length M by 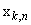 . Each node k also can have access to data from the set of nodes defined as neighborhood
. Each node k also can have access to data from the set of nodes defined as neighborhood 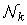 so that they are directly linked to node k. by Combine-Then-Adapt (CTA) form of diffusion protocol, at first, each node k combine the weight vectors from the neighborhood including itself as follows
so that they are directly linked to node k. by Combine-Then-Adapt (CTA) form of diffusion protocol, at first, each node k combine the weight vectors from the neighborhood including itself as follows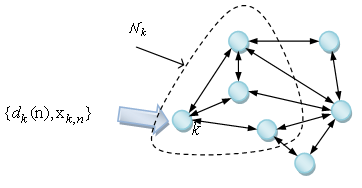 | Figure 1. Diffusion mode of cooperation structure |
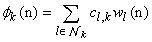 | (11) |
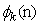 denotes the combinational weight vector in node k which is computed by non-negative real combiner coefficients
denotes the combinational weight vector in node k which is computed by non-negative real combiner coefficients 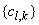 satisfying following conditions
satisfying following conditions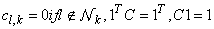 | (12) |
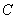 is a
is a 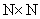 matrix with entries
matrix with entries 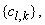 and
and 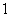 denotes the
denotes the 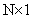 vector with unit entries. Then, in Adapt step, the local weight update at node k can be expressed as
vector with unit entries. Then, in Adapt step, the local weight update at node k can be expressed as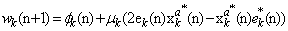 | (13) |
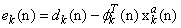 .
.4. Mean Stability Analysis of D-AQLMS Algorithm
- In order to analyze the convergence in the mean of D-AQLMS algorithm, we rewrite the combinational weight vector (11) and weight update (13), by regarding the property (5), in the global form as follows
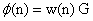 | (14) |
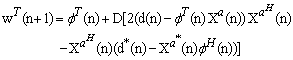 | (15) |
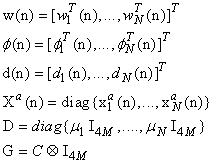 where diag{.} operator denotes the diagonal matrix and
where diag{.} operator denotes the diagonal matrix and 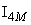 the
the 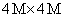 identity matrix with M representing the filter order. We also consider a teaching signal in the global form as a linear model for data as follows
identity matrix with M representing the filter order. We also consider a teaching signal in the global form as a linear model for data as follows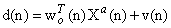 | (16) |
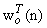 represents the optimal (and unknown) local augmented weight vector, and
represents the optimal (and unknown) local augmented weight vector, and 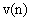 the quadruply white Gaussian noise with zero mean and variance
the quadruply white Gaussian noise with zero mean and variance 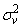 , which assumed to be uncorrelated with
, which assumed to be uncorrelated with 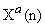 . By substituting the signal (16) into the weight update (15), we have
. By substituting the signal (16) into the weight update (15), we have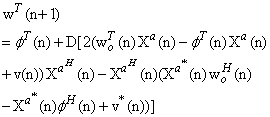 | (17) |
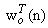 we obtain
we obtain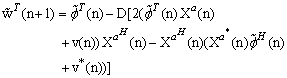 | (18) |
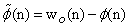 and
and 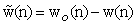 . by substituting the relation (14) into the (18) and then applying the statistical expectation operator we obtain
. by substituting the relation (14) into the (18) and then applying the statistical expectation operator we obtain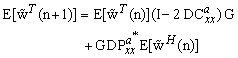 | (19) |
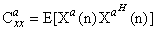 and
and 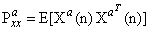 . We have equivalently
. We have equivalently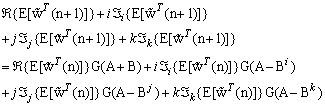 | (20) |
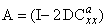 and
and 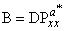 . Where
. Where 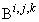 denote the involutions of B and we indeed have used the following property for a given quaternion variable
denote the involutions of B and we indeed have used the following property for a given quaternion variable 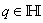
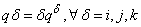 | (21) |
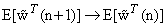 as
as 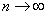 , or equivalently
, or equivalently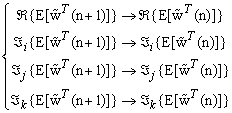 | (22) |
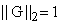 (because the rows and columns add to 1), we must have
(because the rows and columns add to 1), we must have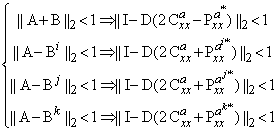 | (23) |
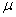 , we can obtain the following lower bounds for the stepsize
, we can obtain the following lower bounds for the stepsize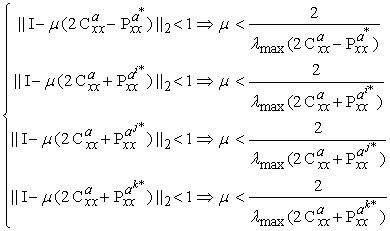 | (24) |
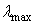 denotes the dominant eigenvalue. Finally, we can say
denotes the dominant eigenvalue. Finally, we can say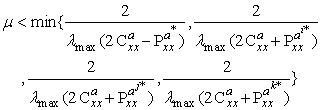 | (25) |
5. Simulations
- In this section, we will compare the performance of proposed algorithm D-AQLMS with its standard linear counterpart (D-QLMS) and non-cooperative case in one step ahead prediction setting. The network include N = 6 nodes, and filter order is set to M = 5. Among the several static combination rules [10], by using network topology in Figure 2, we employ the Metropolis rule described as follows
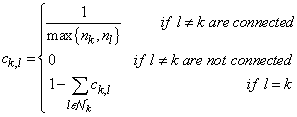 | (26) |
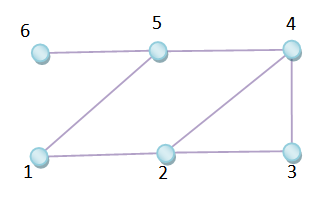 | Figure 2. Diffusion network topology used in simulations |
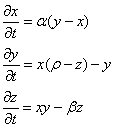 | (27) |
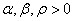 . The other signal is generated by a linear AR(4) model as follows
. The other signal is generated by a linear AR(4) model as follows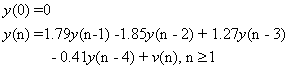 | (28) |
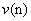 denotes the circular quadruply white Gaussian noise. Figure 3 illustrates the evaluation of mean square error (MSE) of proposed algorithm in analogy to non-cooperative case for one step ahead prediction of the mentioned signals. Observe that as expected the proposed cooperative algorithm outperforms the non-cooperative case. Figure 4 shows the evaluation of MSE for one step ahead prediction of the noncircular Lorenz signal for comparing the proposed algorithm with its standard linear counterpart. It is worth noting that due to non-circular nature of the Lorenz signal, the widely linear distributed algorithm has better performance than standard linear distributed one.
denotes the circular quadruply white Gaussian noise. Figure 3 illustrates the evaluation of mean square error (MSE) of proposed algorithm in analogy to non-cooperative case for one step ahead prediction of the mentioned signals. Observe that as expected the proposed cooperative algorithm outperforms the non-cooperative case. Figure 4 shows the evaluation of MSE for one step ahead prediction of the noncircular Lorenz signal for comparing the proposed algorithm with its standard linear counterpart. It is worth noting that due to non-circular nature of the Lorenz signal, the widely linear distributed algorithm has better performance than standard linear distributed one.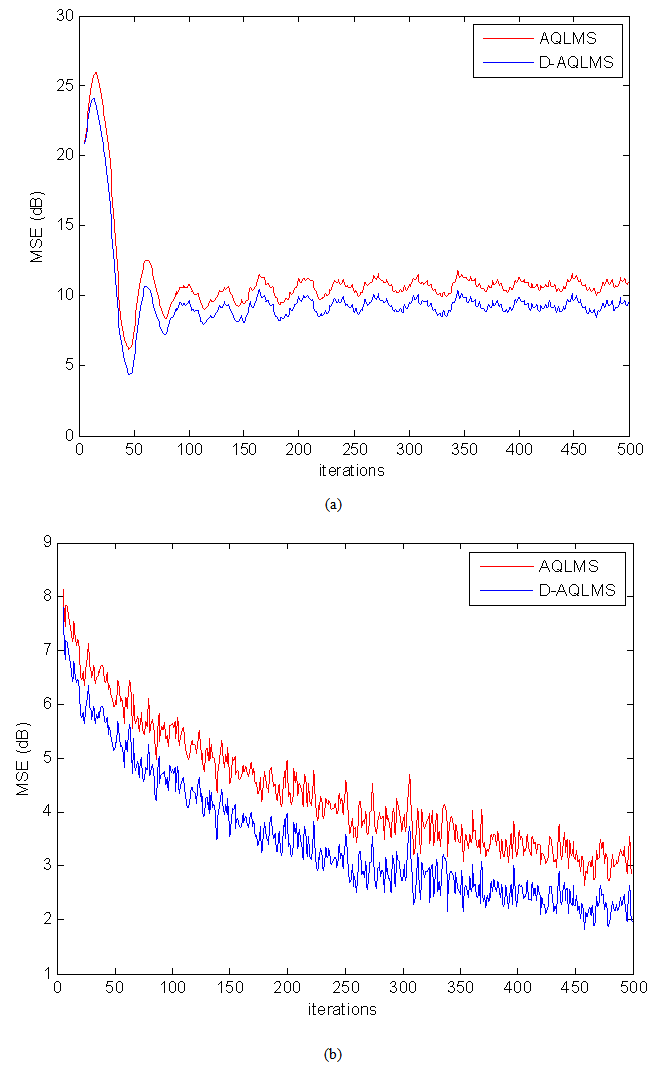 | Figure 3. Comparison of MSEs of non-cooperative AQLMS and Diffusion AQLMS algorithms for prediction of (a) circular 4D AR(4) process with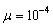 , and (b) noncircular 3D Lorenz signal with , and (b) noncircular 3D Lorenz signal with 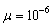 |
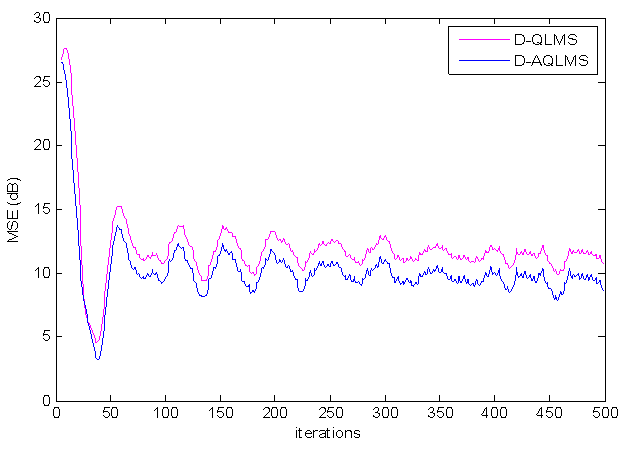 | Figure 4. Comparison of MSEs of D-AQLMS and D-QLMS for prediction of noncircular 3D Lorenz signal with 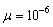 |
6. Conclusions
- We have proposed a Diffusion Augmented QLMS (D-AQLMS) algorithm for distributed processing of both circular and noncircular quaternion-valued signals. The advantage of the widely linear diffusion algorithm over standard linear diffusion and noncooperative case in terms of steady state performance has been shown in simulations on synthetic signals.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
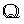 -proper random variable
-proper random variable