1. Introduction

Due to high competition the retention of impatient customers has become a key issue for any business. Insurance business is not exceptional as well. In thrust of maximizing profit companies try to reach more and more customers. Impatient customers may also make some potential customer balk (customers leave without joining the queue) away by communicating their level of dissatisfaction. So companies facing customer impatience are impacted with another blow in form of customer balking resulting in loss of more customers. To minimize above mentioned customer loss, high level of customer service is required and that includes high cost of service, which also varies with rate of service. One way to increase profit is by minimizing the cost. Thus, there is a need to enforce optimum service rate, so that cost of service can be minimized, customers are served more satisfactorily and total profit can be optimized.

Cochran et al.[10] explores the concept of customer impatience and the loss due to this the business faces. Wu et al.[12] focus on an M/M/s queue with multiple vacations such that the server works with different service rates rather than no service during vacation period. They generalize an M/M/1 queue with working vacations. A cost function is formulated to determine the optimal number of servers subject to the stability conditions. Direct search and Newton-Quasi algorithm is applied to find an approximate solution. Same algorithm is applied to investigate the M/M/R machine repair problem with second optional repair by Wang et al.[9]. A cost model is derived to determine the optional number of repairmen, the optimal values of the first essential repair rate, and the second optional repair rate while maintaining the system availability at a specified level. Ke et al.[8] construct the membership functions of the system characteristics of a heterogeneous-server queuing model with fuzzy customer arrival and service rates. Ching et al.[7] find that when the marginal cost of service capacity is low relatively to the revenue per customer, a unique Nash equilibrium exists, in which all servers choose the same service capacity and the expected waiting times are finite. Tadj et al.[11] use a vacation queuing model and develop a set of quantitative performance measures for a two-parameter time allocation policy. Based on the renewal cycle analysis, they derive an average cost expression and propose a search algorithm to find the optimal time allocation policy that minimizes the average cost. Yue et al.[6] study a two-server Markovian network system with balking and a Bernoulli schedule under a single vacation policy, where servers have different service rates. Yue et al. further in[4] present analysis for an M/M/R/N queuing system with balking, reneging and server breakdowns. A cost model is developed to determine the optimum number of servers while the system availability is maintained at a certain level.

Wang et al. in[1] develop a cost model for an M/M/R queuing system with finite capacity balking, reneging and server breakdowns. Sensitivity analysis of the model along with numerical results is also performed. Pan[5] studies an M/M/1/N queuing model with variable input rates and points out the appropriate service speeds for the business. Yue et al.[3] present an analysis for an M/M/c/N queuing system with balking, reneging and synchronous vacations of partial servers together formulate a cost model to determine the optimal number of servers on vacation. They perform sensitivity analysis through numerical experiments. Literature survey shows the importance of cost modeling and its solution in way to optimize profit. Borst et al.[2] apply queuing theory for designing the call centers. Recently, Kumar and Sharma[13] study a single server, finite capacity Markovian queuing model with retention of reneged customers and balking and derive its steady state solution.

2. Description of the Model

In this paper, we propose a single server, finite capacity Markovian queuing model with retention of reneged customers and balking for any insurance firm facing the problem of customer impatience (reneging and balking) and implementing different customer retention strategies as studied by Kumar and Sharma[13]. The customers arrive in the system according to a Poisson process with mean rate λ. An arrival to the system represents the sale of one insurance policy. There is a single server and the customers are served in order of their arrival The service time distribution is exponential with parameter μ. Here, the service of a customer represents the claim processing at the maturity of the policy. The insured customers at any stage before maturity may get impatient due to various reasons like dissatisfaction of service, immediate requirement of money, better opportunities with the other insurers etc. and withdraw them. This phenomenon is analogous to reneging in case of queuing theory. The customers get impatient (reneged) following exponential distribution with parameter ξ. As the customer impatience has highly negative impact on the business of the firms, they employ different customer retention strategies to retain their customers. It is envisaged that if the firms employ certain customer retention strategies, then there are chances that a certain proportion of impatient customers may be retained. Thus, an impatient customer may be retained in the system with some probability q (say) and he may not be convinced to stay in the system for his complete service with probability 1 – q (= p). The customer retention strategies in insurance business can be the convincing of customers by phone, better and reliable service, providing better returns, discounts on premium etc. The arriving customers balk with probability n/N, where n is the number in system and N is the maximum number allowed in the system (i.e. some customer may not decide to purchase the policy due to dissatisfaction about company policies).

The steady state probabilities of the models are given by:

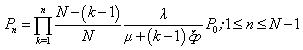(1)

Also for n=N, we get

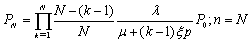(2)

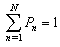Using the normalization condition, , we get

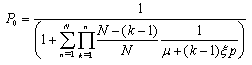(3)

The expected system size is:

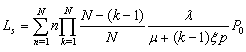(4)

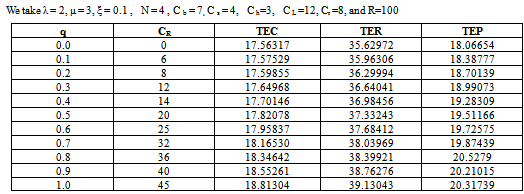
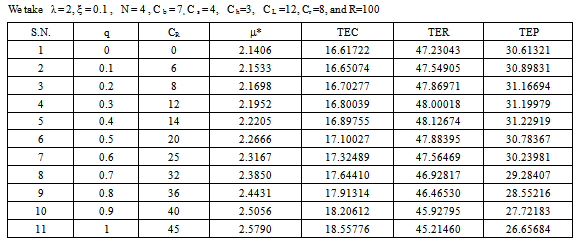
3. Cost Model

In this section, we present the cost-model and perform optimization.

Notations:

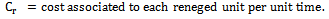
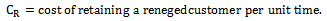
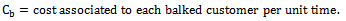
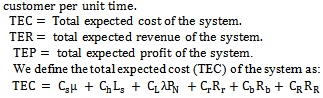Where the average reneging rate R_r , the average retention rate R_R and the average balking rate are given by;

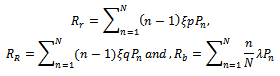Let R be the revenue earned for providing service to each customer per unit time, then RL_s is the total earned revenue by providing service to average number of customers in the system. Rλ P_N, RR_r and RR_b are the losses in the revenue of the system due to number of lost customers per unit time, due to reneging of customers and due to balking of customers per unit time respectively. Hence, total expected revenue (TER) of the system is given by:

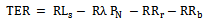Now, total expected profit (TEP) of the system is defined as:

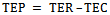Thus, we have the TEC, TER and TEP functions in terms of various parameters involved. The cost – profit analysis of the model is performed numerically by using these functions and the results are discussed accordingly. The optimization of the model is also carried out in order to obtain the optimal service rate and to obtain the optimum values of TEC, TER and TEP. The impact of various customer retention strategies on the total optimal profit is also analyzed. It becomes quiet intractable to proceed analytically for optimum value of service rate (μ*) at which the TEC is minimum. Therefore, we have used MATLAB software to get the optimum values using a computational algorithm.

Computational algorithm:

Step 1: Define variables

Step 2: Write the formula of function TEC in terms of μ

Step 3: Obtain critical values for TEC

Step 4: Find the value of μ at which TEC is minimum (let it be μ*)

Step 5: Compute the values of TEC, TER and TEP at μ*

Table 1. Variation in TEC, TER and TEP with the change in probability of customer retention, q

Table-1 presents the cost-profit analysis of the model and the effect of customer retention strategies on the total expected profit. It is obvious that a better customer retention strategy involves higher retention cost than the others. Therefore, in the third column of the table we have associated different customer retention costs to different strategies. It is observed that as the probability of customer retention associated with a particular strategy increases the total expected profit of the system also increases. When the probability of customer retention is zero, the total expected profit is minimum. This is the case of no customer retention. When q = 1 the total expected profit is maximum. In this case all the reneged customers are retained. Thus, one may have a snapshot of the long run performance of different customer retention strategies on the business.

Table 2. Variation in TEC, TER and TEP with the change in probability of customer retention, q at optimal service rate

We have performed the optimization of the model under investigation to determine the optimum service rate, and the optimal values of total expected revenue, total expected cost and total expected profit. A computational algorithm translated in MATLAB is used to obtain the optimum values. In table – 1, a simple cost-profit analysis of the model is presented, while in table-2 t he optimum results are presented. As the probability of customer retention increases, the optimum service rate also increases. This may be attributed to the fact that the increase in probability of customer retention leads to the increase in the number of customers in queue and therefore higher, service rate is needed to serve more and more customers for revenue generation.

It can be observed that the total expected cost increases with increase in the probability of customer retention from q = 0 to q = 1. This is due to the fact that the cost of customer retention strategies also increases. The total expected profit increases regularly from q = 0 to q = 0.4. It attains maximum value at q = 0.4 and μ* = 2.2205 and then decreases gradually. This is the optimum choice of probability of customer retention and the service rate at which the customers must be served to maximize the profit. Thus one can choose the best customer retention strategy from among many.

4. Conclusions

A queuing theory approach is used to model insurance business problems. A single server finite capacity Markovian queuing model with retention of reneged customers, and balking is proposed for any insurance firm facing the problem of customer impatience (reneging and balking) and implementing different customer retention strategies.

The cost – profit analysis of the model is performed and the impact of various customer retention strategies on the total expected profit of the system is studied.

The optimization of the model is performed in order to minimize the total expected cost of the system with respect to the service rate. The analysis carried out in this paper is very useful to any insurance firm, as it helps to choose the best customer retention strategy.

The model can further be optimized for other parameters available.