Gulab Singh Bura1, Rakesh Kumar2
1Deptartment of Mathematics & Statistics, Banasthali University, Rajasthan, India
2School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320, Jammu and Kashmir, India
Correspondence to: Rakesh Kumar, School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320, Jammu and Kashmir, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we have obtained the time- dependent solution of a varying catastrophic intensity-cum- restorative Markovian queueing model with finite capacity. The transient solution has been obtained recursively. The simulation of the model has also been performed and various measures of performance have been computed. The steady-state solution is also derived. Further, some particular cases of the queuing model have been derived and discussed.
Keywords:
Varying Catastrophic Intensity, Restoration Time, Markovian Queueing System, Steady State Solution
Cite this paper: Gulab Singh Bura, Rakesh Kumar, Transient Analysis of a Limited Capacity Markovian Queueing System Subjected to Varying Catastrophic Intensity and Restoration, American Journal of Operational Research, Vol. 3 No. A, 2013, pp. 34-43. doi: 10.5923/s.ajor.201305.05.
1. Introduction
During the last three decades the attention of the queueing models has been focused on certain extension that includes the effect of catastrophes, in particulars, birth and death models. A large number of research papers have been published on population processes under the influence of catastrophes, for instance, Swift[12], Kyriakidis[3], Brockwell[9, 10, and 11] among other have discussed birth and death models with catastrophes. Queuing models continue to be one of the most important area of computer networks and have played a vital role in performance evaluation of computer systems. In computer system, if a job is infected, this job may transmit virus which may be transferred to the other processors. Hence computer network with virus may be modeled by queuing networks with catastrophes[2]. In the above mentioned research work the authors has assumed that the random occurrence of catastrophe destroys all the customers in a queuing system. But it is not always the case. So, necessary amendment is incorporated by Jain and Bura[6, 7] in the form of varying catastrophic intensity to destroy a finite number of customers at a time. The number of customers in a queuing system is instantly reset to zero or not depends upon the intensity of catastrophe. Queuing models with varying catastrophic intensity are applied in various field of biological sciences and agriculture. The concept of restoration time is considered by Jain and Kumar[8]. If the catastrophic intensity destroys all the customers in a queuing system then the system will require some sort of time to function in a normal way, which is taken as restoration time. Hence, an assumption of restoration is added in addition to the assumption of varying catastrophic intensity. In restoration case, we assume that during the restoration time no arrival is allowed to occur.
2. Queuing Model
The queuing model investigated in this paper is based on the following assumptions:-(i) The customers arrive in the system one by one in accordance with a Poisson process at a single service station with rate 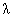 > 0. (ii) The customers are served one by one by a single server and the service times are independently, identically, and exponentially distributed with rate
> 0. (ii) The customers are served one by one by a single server and the service times are independently, identically, and exponentially distributed with rate 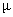 > 0.(iii) When the system is not empty, catastrophes occur according to a Poisson process with rate and intensity Cr ,
> 0.(iii) When the system is not empty, catastrophes occur according to a Poisson process with rate and intensity Cr , 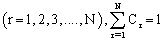 . It depends upon the intensity of the catastrophe whether it destroys all the customers or not. If it destroys all the customers, then the system will require some sort of time to re-function in a normal way, which is taken as restoration time.(iv) The restoration time is independently, identically and exponentially distributed With parameter
. It depends upon the intensity of the catastrophe whether it destroys all the customers or not. If it destroys all the customers, then the system will require some sort of time to re-function in a normal way, which is taken as restoration time.(iv) The restoration time is independently, identically and exponentially distributed With parameter 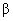 . During the restoration time no arrival is allowed to occur.(v) The queue discipline is first- come first- served.(vi) The capacity of the system is limited to N. i.e., if at any instant there are N customers in the system, then the customers arriving in the duration for which the system remains in state N are not permitted to join the queue and considered lost for the system with probability one.(vii) Initially, there are zero customers in the system.Define
. During the restoration time no arrival is allowed to occur.(v) The queue discipline is first- come first- served.(vi) The capacity of the system is limited to N. i.e., if at any instant there are N customers in the system, then the customers arriving in the duration for which the system remains in state N are not permitted to join the queue and considered lost for the system with probability one.(vii) Initially, there are zero customers in the system.Define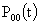 = the probability that there are zero customer in the system at time t without the occurrence of catastrophe.
= the probability that there are zero customer in the system at time t without the occurrence of catastrophe.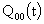 =the probability that there are zero customer in the system at time t with the occurrence of catastrophe destroying all the customers.
=the probability that there are zero customer in the system at time t with the occurrence of catastrophe destroying all the customers.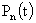 =the probability that there are n customers in the system at time t.
=the probability that there are n customers in the system at time t.
3. Transient Solution
The differential-difference equations governing the system are: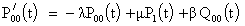 | (1) |
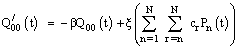 | (2) |
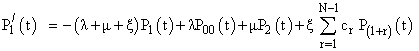 | (3) |
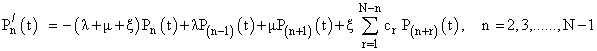 | (4) |
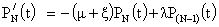 | (5) |
Taking, Laplace Transform of equations (1), to (5) w.r.t.‘t’, we have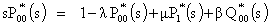 | (6) |
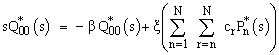 | (7) |
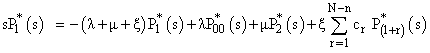 | (8) |
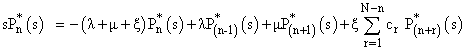 | (9) |
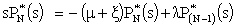 | (10) |
Where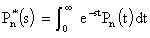 and
and  Solving this set of equations recursively, we have
Solving this set of equations recursively, we have | (11) |
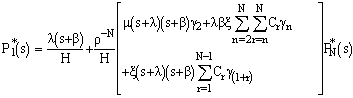 | (12) |
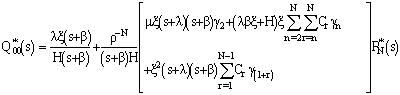 | (13) |
and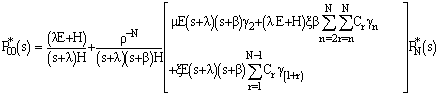 | (14) |
Where 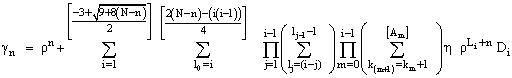
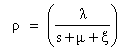 ,
, 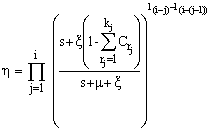 ,
, 
 An integral function.
An integral function.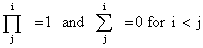 ,
, 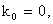
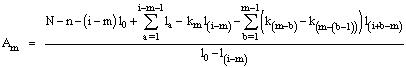
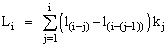 ,
, 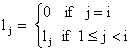 ,
, 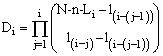
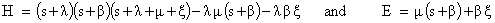 Using normalization condition, we have
Using normalization condition, we have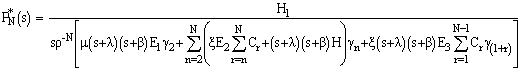 | (15) |
Where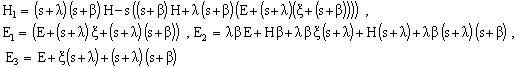 Using (15) in (11) to (14) we have
Using (15) in (11) to (14) we have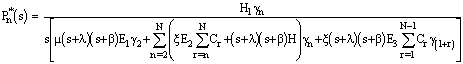 | (16) |
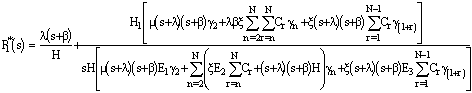 | (17) |
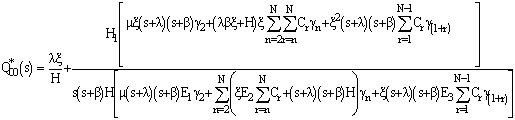 | (18) |
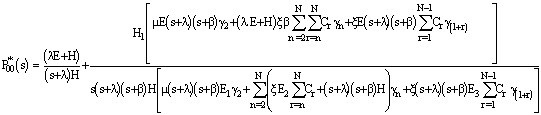 | (19) |
After taking Laplace inverse of (16) to (19), we can find all the probabilities.
4. Simulation Results
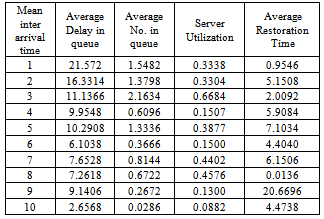
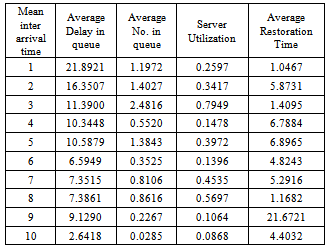
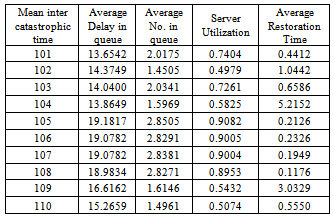
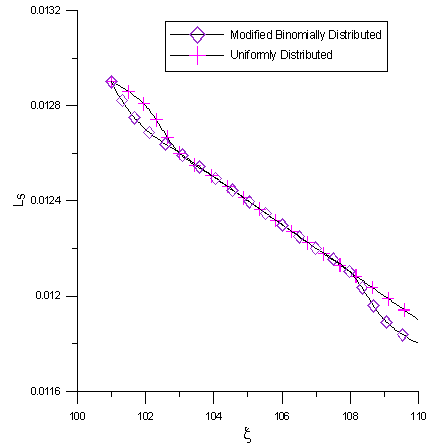
We obtain numerically the various measures of performance i.e. average delay in queue, average no. in queue; sever utilization time and average restoration time of this model by using simulation technique. The simulation analysis of the queueing model under investigation is carried out by using a computer program written in C language. The simulation results have been shown in tables 1-6. In tables 1-3, the simulation results are obtained by assuming that the catastrophic intensity follows the uniform distribution while in tables 4-6, the simulation results are obtained by assuming that the catastrophic intensity follows the modified binomial distribution. Table 1.
 |
| |
|
In Table- 1we obtained the various measures of an M/M/1/N queueing model with uniformly distributed catastrophic intensity subjected to restoration for the effect of change in means inter arrival time  for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.Table 2.
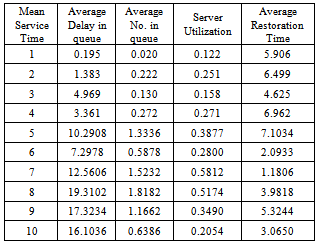 |
| |
|
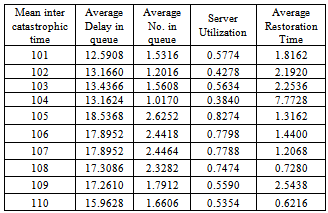
In Table- 2 we obtained the various measures of an M/M/1/N queueing model with uniformly distributed catastrophic intensity subjected to restoration for the effect of change in means inter service time 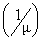 for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.Table 3.
 |
| |
|
In Table- 3 we obtained the various measures of an M/M/1/N queueing model with uniformly distributed catastrophic intensity subjected to restoration for the effect of change in means inter catastrophe time 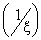 for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.
for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.Table 4.
 |
| |
|
In Table- 4 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter arrival time 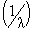 for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.Table 5.
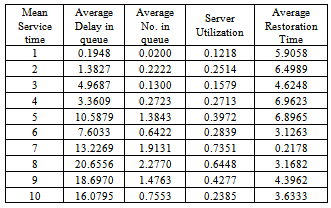 |
| |
|
In Table- 5 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter service time 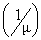 for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.In Table-6 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter catastrophe time
for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.In Table-6 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter catastrophe time 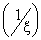 for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.
for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.Table 6.
 |
| |
|
5. Steady State Solution
Using the property 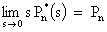 , We have from (16) to (19)
, We have from (16) to (19)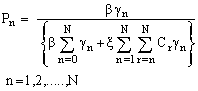 | (20) |
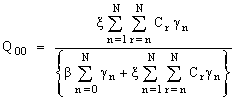 | (21) |
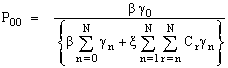 | (22) |
6. Measures of Effectiveness
The steady state probability distribution for the system size allows us to calculate what are commonly called measures of effectiveness. Two, of immediate interest are the expected number of customers in the system and the expected number of customers in the queue. To derive the foregoing measures, let Ls represents the expected number in the system and Lq represents the expected number in the queue. Thus we have 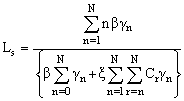 and
and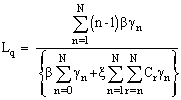
7. Important Particular Cases of the Model
(I) In case the catastrophic intensity follows the uniform distribution then we get: 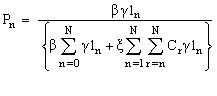
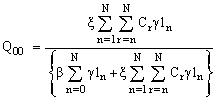
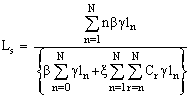
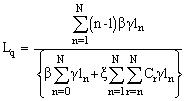 Where
Where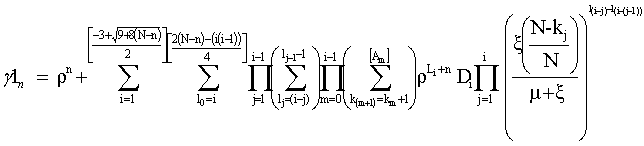 (II) In case the catastrophic intensity follows the modified binomially distribution then we get:
(II) In case the catastrophic intensity follows the modified binomially distribution then we get: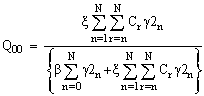
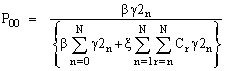
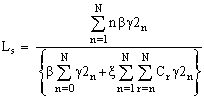
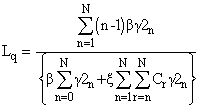 Where
Where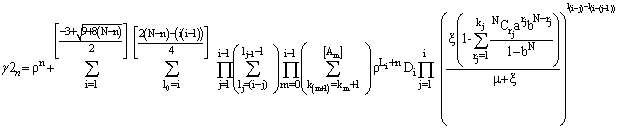
8. Graphical Presentation
So far, we have obtained explicit expression for P00, Q00, Pn n=1, 2… N. The steady state probabilities of the system size, Ls, the mean number of customers in the system, Lq, the mean number of customers in the queue for both the cases in which the catastrophic intensity follows (I) the uniform distribution (II) the modified binomial distribution. Now here, we present some graphical presentation to highlight the effects of the catastrophe parameter 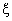 , the arrival rate
, the arrival rate 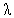 and the service rate
and the service rate 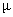 on P00, Q00 and Ls for N = 8.In fig. 1, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
on P00, Q00 and Ls for N = 8.In fig. 1, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of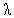 . P00 decreases as the arrival rate
. P00 decreases as the arrival rate 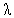 increases.In fig. 2, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
increases.In fig. 2, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of 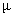 . P00 increases with the increase in service rate
. P00 increases with the increase in service rate 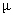 In fig. 3, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
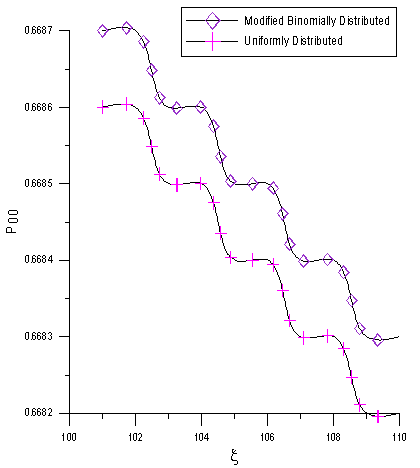
In fig. 3, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of 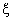 . P00 decreases as the catastrophe rate
. P00 decreases as the catastrophe rate 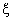 increases.In fig. 4, we illustrate the effect of the arrival rate
increases.In fig. 4, we illustrate the effect of the arrival rate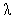 , on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of
, on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of 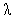
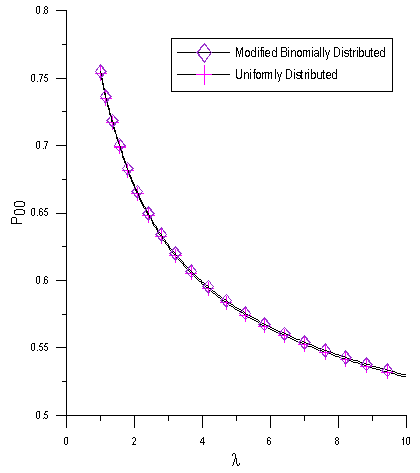 | Figure 1. P00 as a function of  for for  |
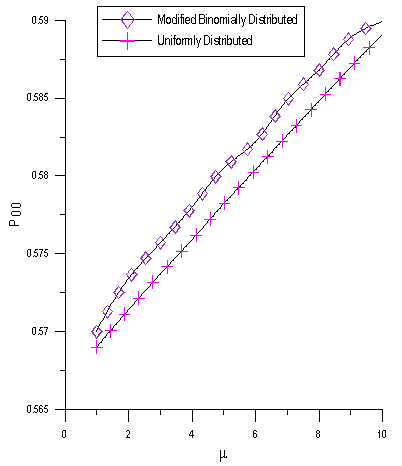 | Figure 2. P00 as a function of 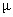 for for 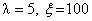 |
 | Figure 3. P00 as a function of 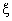 for for 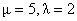 |
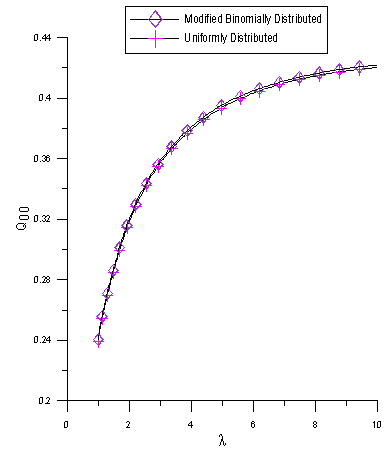 | Figure 4. Q00 as a function of for 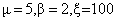 |
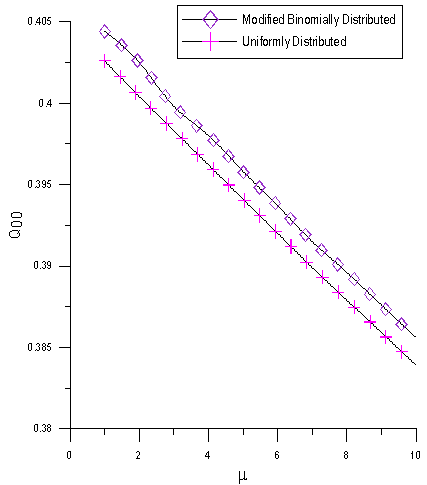 | Figure 5. Q00 as a function of 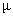 for for 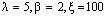 |
In fig. 5 we illustrate the effect of service rate 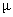 on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is a decreasing function of
on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is a decreasing function of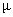 .
.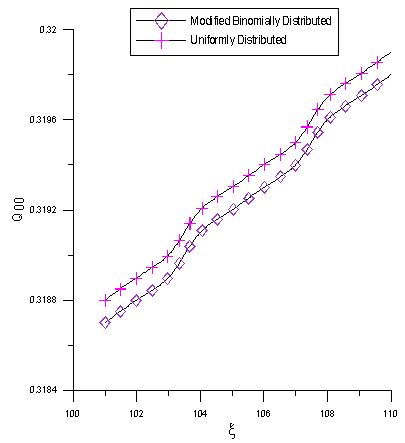 | Figure 6. Q00 as a function of 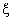 for for 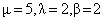 |
In fig. 6 we illustrate the effect of the catastrophe rate 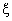 on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of
on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of 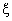 .
.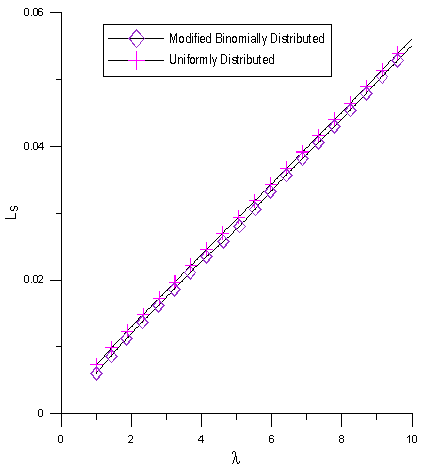 | Figure 7. Ls as a function of 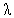 for for 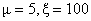 |
In fig. 7 we illustrate the effect of the arrival rate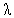 on Ls. It has been noticed that Ls is an increasing function of
on Ls. It has been noticed that Ls is an increasing function of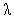 .
.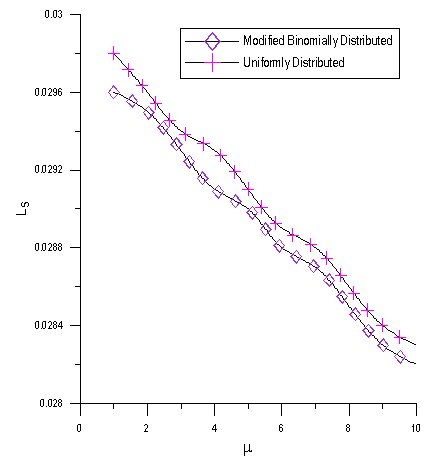 | Figure 8. Ls as a function of 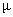 of for of for 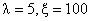 |
In fig. 8 we illustrate the effect of the service rate 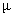 on Ls. It has been noticed that Ls is a decreasing function of
on Ls. It has been noticed that Ls is a decreasing function of 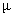 .
.  | Figure 9. Ls as a function 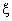 for for 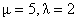 |
In figs. 9 we illustrate the effect of the catastrophe rate 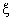 on Ls. It has been noticed that Ls is a decreasing function of
on Ls. It has been noticed that Ls is a decreasing function of 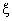 .
.
9. Conclusions
In the present paper, we have studied a varying catastrophic intensity-cum- restorative Markovian queueing model with finite capacity. The concept of varying catastrophic intensity has numerous applications in a wide variety of areas particularly in agriculture and biosciences etc. In agriculture, if a crop is infected with some disease then for the treatment of such type of disease we use some chemicals. The destruction of the number of bacteria present in the crops depends upon the intensity of the chemicals used, that is, the application of the chemical may destroy all or a part there of. The use of the chemicals is like the occurrence of catastrophe. Therefore the infected crops with use of chemical are modeled by the birth and death queue with varying catastrophic intensity. With the introduction of restoration time the practical utility of the model is considerably increased.
References
| [1] | A. Di Crescenzo, V. Giorno, A.G. Nobile, and L.M. Ricciardi, “On the M/M/1 queue with catastrophes and its continuous approximation”, Queuing System, vol. 43, pp. 329- 347, 2003. |
| [2] | B. Krishna Kumar, and D. Arivudainambi, “Transient solution of an M/M/1 queue with catastrophes”, Computers & Mathematics with Application, vol. 40, pp. 1233-1240, 2000. |
| [3] | E.G., Kyriakidis, “Stationary probabilities for a simple immigration birth-death process under the influence of total catastrophes”, Statistics & Probability Letters, vol. 20, issue 3, pp. 239-240, 1994. |
| [4] | M. Law, and W. D. Kelton, “Simulation modeling and analysis”, 3rd edition, McGraw Hill Book Company, New York. 2003. |
| [5] | Narsingh Deo, “System simulation with digital computer”, Prentice hall of India Private. Ltd, 2007. |
| [6] | N.K. Jain, and Gulab Singh Bura, “A queue with modified binomially distributed Catastrophic intensity”, International Journal. of Statistics and Systems, vol. 4, No.2, pp. 111-116, 2009. |
| [7] | N.K. Jain and Gulab Singh Bura, “A queue with varying catastrophic intensity”, International journal of computational and applied mathematics, vol. 5, No.1 pp. 41-46, 2010. |
| [8] | N.K. Jain and Rakesh Kumar, “Transient solution of a catastrophic-cum-restorative queuing problem with correlated arrivals and variable service capacity”, International Journal of Information and Management Sciences, Taiwan, vol. 18, no. 4, pp. 461- 465, 2007. |
| [9] | P.J., Brockwell, “The extinction time of a birth, death and catastrophe process and of a related diffusion model”, Advance in Appliied. Probability, vol. 17, pp. 42-52, 1985. |
| [10] | P.J, Brockwell, The extinction time of a general birth and death process with Catastrophe”, Journal of Applied Probability, vol. 23, pp. 851-858, 1986. |
| [11] | P.J. Brockwell, J. Gani, and S.I, Resnick, “Birth immigration and catastrophe Process”. Advance in Applied Probability, vol. 14, pp. 709-731, 1982. |
| [12] | R.G., Swift, “Transient probabilities for simple birth-death immigration process under the influence of total Catastrophes”, International Journal of Mathematics & Mathematical Sciences, vol. 25, No. 10, pp. 689- 692, 2001. |

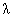 > 0. (ii) The customers are served one by one by a single server and the service times are independently, identically, and exponentially distributed with rate
> 0. (ii) The customers are served one by one by a single server and the service times are independently, identically, and exponentially distributed with rate 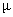 > 0.(iii) When the system is not empty, catastrophes occur according to a Poisson process with rate and intensity Cr ,
> 0.(iii) When the system is not empty, catastrophes occur according to a Poisson process with rate and intensity Cr , 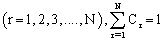 . It depends upon the intensity of the catastrophe whether it destroys all the customers or not. If it destroys all the customers, then the system will require some sort of time to re-function in a normal way, which is taken as restoration time.(iv) The restoration time is independently, identically and exponentially distributed With parameter
. It depends upon the intensity of the catastrophe whether it destroys all the customers or not. If it destroys all the customers, then the system will require some sort of time to re-function in a normal way, which is taken as restoration time.(iv) The restoration time is independently, identically and exponentially distributed With parameter 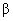 . During the restoration time no arrival is allowed to occur.(v) The queue discipline is first- come first- served.(vi) The capacity of the system is limited to N. i.e., if at any instant there are N customers in the system, then the customers arriving in the duration for which the system remains in state N are not permitted to join the queue and considered lost for the system with probability one.(vii) Initially, there are zero customers in the system.Define
. During the restoration time no arrival is allowed to occur.(v) The queue discipline is first- come first- served.(vi) The capacity of the system is limited to N. i.e., if at any instant there are N customers in the system, then the customers arriving in the duration for which the system remains in state N are not permitted to join the queue and considered lost for the system with probability one.(vii) Initially, there are zero customers in the system.Define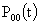 = the probability that there are zero customer in the system at time t without the occurrence of catastrophe.
= the probability that there are zero customer in the system at time t without the occurrence of catastrophe.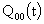 =the probability that there are zero customer in the system at time t with the occurrence of catastrophe destroying all the customers.
=the probability that there are zero customer in the system at time t with the occurrence of catastrophe destroying all the customers.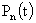 =the probability that there are n customers in the system at time t.
=the probability that there are n customers in the system at time t.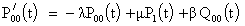
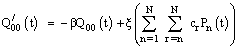
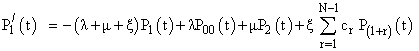
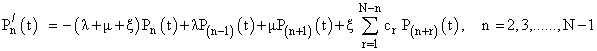
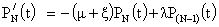
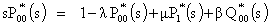
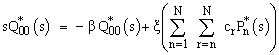
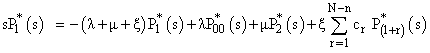
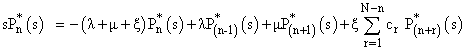
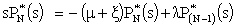
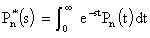 and
and 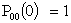 Solving this set of equations recursively, we have
Solving this set of equations recursively, we have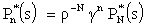
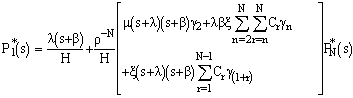
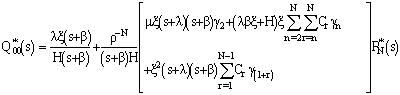
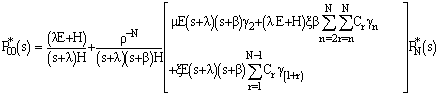
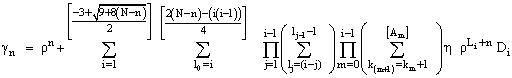
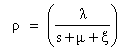 ,
, 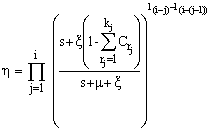 ,
, 
 An integral function.
An integral function.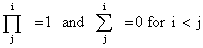 ,
, 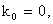
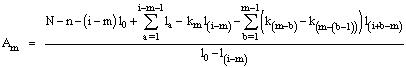
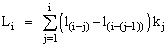 ,
, 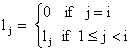 ,
, 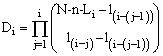
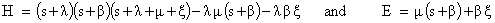 Using normalization condition, we have
Using normalization condition, we have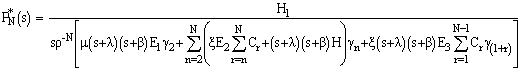
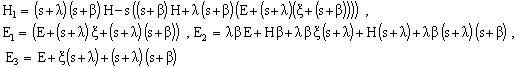 Using (15) in (11) to (14) we have
Using (15) in (11) to (14) we have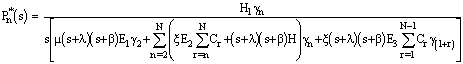
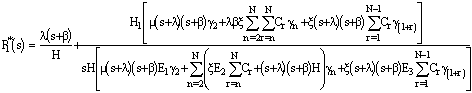
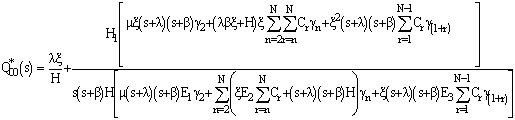
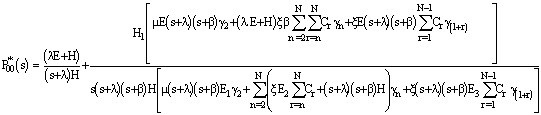
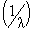 for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.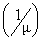 for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.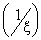 for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.
for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.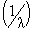 for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.
for fixed mean service time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.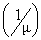 for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.In Table-6 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter catastrophe time
for fixed mean inter arrival time = 5 minutes, mean inter catastrophe time= 100 minutes, simulation length= 480 and N=5.In Table-6 we obtained the various measures of an M/M/1/N queueing model with modified binomially distributed catastrophic intensity subjected to restoration for the effect of change in means inter catastrophe time 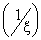 for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.
for mean inter arrival time = 2 minutes, mean service time= 5 minutes, simulation length= 480 and N=5.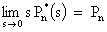 , We have from (16) to (19)
, We have from (16) to (19)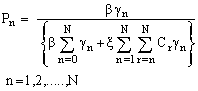
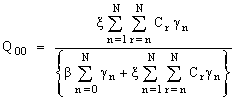
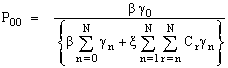
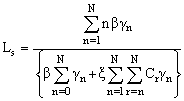 and
and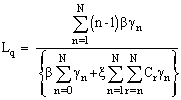
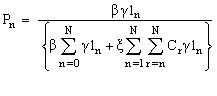
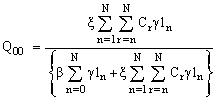
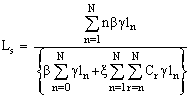
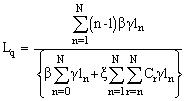 Where
Where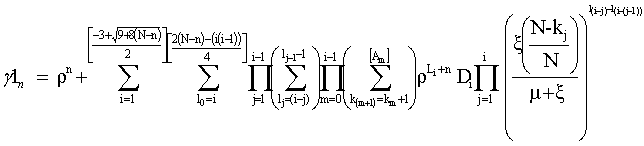 (II) In case the catastrophic intensity follows the modified binomially distribution then we get:
(II) In case the catastrophic intensity follows the modified binomially distribution then we get: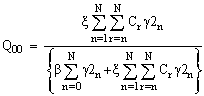
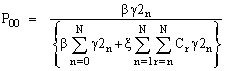
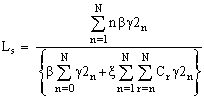
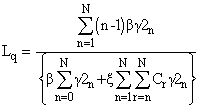 Where
Where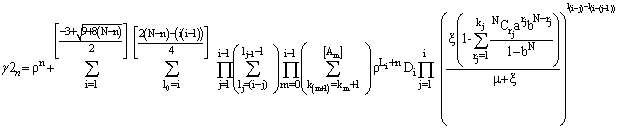
 , the arrival rate
, the arrival rate 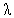 and the service rate
and the service rate 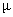 on P00, Q00 and Ls for N = 8.In fig. 1, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
on P00, Q00 and Ls for N = 8.In fig. 1, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of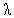 . P00 decreases as the arrival rate
. P00 decreases as the arrival rate 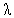 increases.In fig. 2, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
increases.In fig. 2, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of 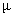 . P00 increases with the increase in service rate
. P00 increases with the increase in service rate 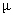 In fig. 3, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of
In fig. 3, we plot the behavior of the probability P00, the probability of zero customers in the system without the occurrence of catastrophe, as a function of 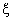 . P00 decreases as the catastrophe rate
. P00 decreases as the catastrophe rate 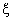 increases.In fig. 4, we illustrate the effect of the arrival rate
increases.In fig. 4, we illustrate the effect of the arrival rate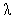 , on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of
, on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of 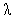

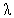 for
for 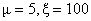

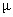 for
for 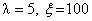

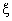 for
for 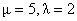

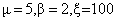

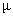 for
for 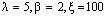
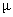 on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is a decreasing function of
on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is a decreasing function of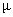 .
.
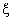 for
for 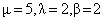
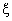 on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of
on Q00, the probability of zero customers in the system with the occurrence of catastrophe. It has been observed that Q00 is an increasing function of 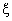 .
.
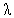 for
for 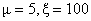
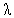 on Ls. It has been noticed that Ls is an increasing function of
on Ls. It has been noticed that Ls is an increasing function of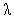 .
.
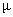 of for
of for 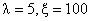
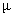 on Ls. It has been noticed that Ls is a decreasing function of
on Ls. It has been noticed that Ls is a decreasing function of 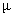 .
. 
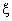 for
for 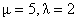
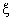 on Ls. It has been noticed that Ls is a decreasing function of
on Ls. It has been noticed that Ls is a decreasing function of 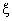 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML




