1. Introduction

In the present work, a two-state multiple vacation queueing system is studied where departures occur in batches of variable size. There are many physical situations where the server has to take vacations to complete some other important work or for its own maintenance after completing the service in hand and when there is no customer waiting in the queue.

Pegden and Rosenshine[1] have given the probability of exact number of arrivals and departures by a given time for the classical queueing model M/M/1/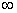.This measure supplies better insight into the behavior of a queuing system than the probability of the exact number of units in the system at a given time, studied in early literature on queues, in many practical situations and therefore more justified.

The early literature on queues with single-state and two-state deal with queuing systems in which arrivals and departures occur one by one. However in many of the practical situations the arrivals and departures occur in batches of variable size. The case when the arrivals occur in batches of fixed size has been considered by Foster[2] and Conolly[3]. Also Bailey[4] and Jaiswal[5-6] havesuccessfully attempted the case when the departures occur in batches of fixed size. Sharda[7] has studied the queuing system by assuming that arrivals and departures occur in batches of variable size. Vijay[8] presents a survey on bulk queues. Recently, Murthy et. al.[9], Gupta and Banerjee[10-11] study bulk service queues.

Also, in recent studies server’s idle time is utilized for the purpose of performing some other jobs. These studies, however, do not consider the case when the server has to go for performing other important jobs or for its own maintenance even when the queue length is not zero and these queuing systems correspond to those practical situations where the server is supposed to handle other jobs in addition to the primary jobs requiring attention and the period during which the server attends the other jobs, starting from the time point when there are no primary jobs, up to the time point of its return for again performing the primary jobs, is called the vacation period in present day literature. The interest in such queuing systems further enhanced by its applications in computer, communication, production and other stochastic systems.

The concept of vacation time was introduced by Cooper[12] in 1970 and studied by Levy and Yechiali[13], Scholl and Kleinrock[14], Lee[12], B.T. Doshi[15], Baba[16], Chae K.C.,Lee H.W.,Ahn C.W.[17], Takin T.[18] and Choudhury G.[19] etc. However, the above mentioned authors study only the steady-state aspect of the queuing problems dealing with vacation times. Keilson and Servi[20] seems to be the first to talk about transient aspect of the queuing problems related with vacation times.

Following[1] &[9], Sharda and Indra[21-23] obtained the transient solution of two-state (i) multiple vacation queuing systems and (ii) multiple vacation queuing systems with intermittent available server. Ayyappan and Sridevi[24] study bulk service queues with vacations. Vijay[25] also obtained transient solution of two-state bulk queueing systems with vacations.

A practical situation corresponding to the present queueing model can be in the branch of an insurance company. In this the customer executive (C.E.) gets insurance proposal forms (IPF) one by one. After scrutinizing, the C.E. send a batch of forms to the under writing department. Whenever the C.E. has no forms at that time s/he can do other branch operational work, i.e. communication between insurance company and the branch employees.

C.E. corresponds to the server and IPF as customers and the time when the C.E. is doing other branch operational work in the absence of IPF is considered as a vacation time.

The present study attempts to consider all the above possibilities simultaneously. We obtain the transient probabilities of exact number of arrivals and departures in a given time on a first-come-first-serve single server multiple vacation queueing system with departures occurring in batches of variable size.

2. The Model

The queueing system investigated here is described by the following assumptions.

• Arrivals are occurring one-by-one according to Poisson process with parameter.

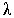• Queue discipline is first-come-first-served.

• The availability of the server/service channel follows an exponential distribution with parameter v.

• The capacity of the service channel is a random variable. The size of the batch is determined at the beginning of each service and is either equal to the total number of units waiting or to the capacity of the service channel determined afresh before each service whichever is less. The probability that the service channel can serve y units is a_y, where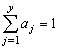, y is the maximum capacity of the server.

• Service time distribution is exponential with parameter.

• The various stochastic processes involved a) arrival of units b) departure of units and c) vacation time of the server/ service channel are statistically independent.

2.1. Definitions and Notations

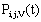= Probability that there are exactly i arrivals and j departures by time t and the server is on vacation; .

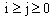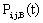= Probability that there are exactly i arrivals and j departures by time t and the server is busy in relation to the queue; .

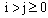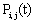= Probability that there are exactly i arrivals and j departures by time t; .

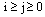The Laplace inverse-transform of 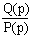is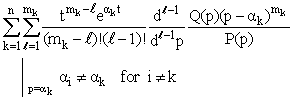

where,

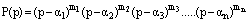and 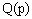is polynomial of degree

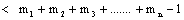If 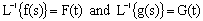, then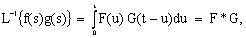

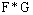is called the convolution of F and G

The Laplace inverse of

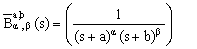is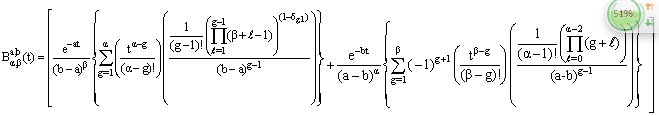

The Laplace inverse of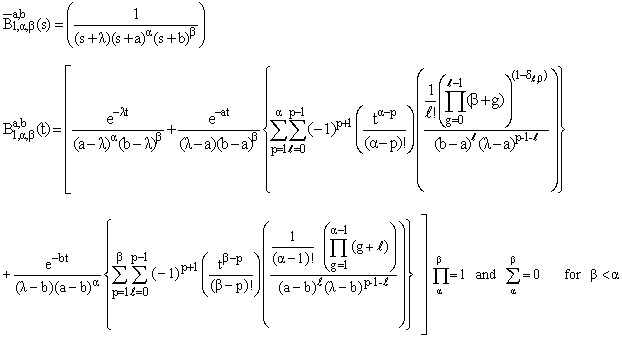

3. Solution of the Problem

Initially,

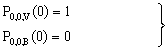(1)

Difference-differential equations governing the system are

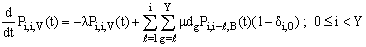(2)

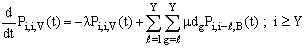(3)

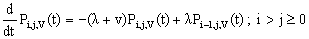(4)

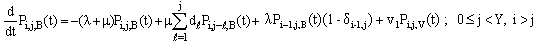(5)

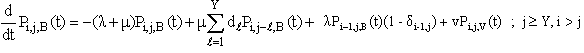(6)

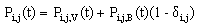Taking Laplace transform of equations (2) to (6) along with (1) and solving,

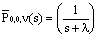(7)

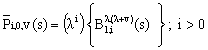(8)

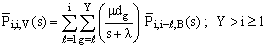(9)

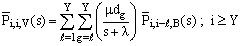(10)

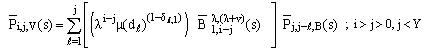(11)

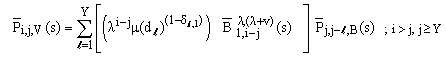(12)

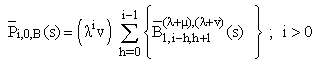(13)

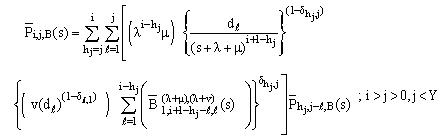(14)

(15)

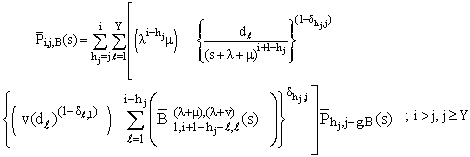Taking Laplace inverse transforms of equations (7) to (15),

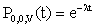(16)

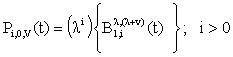(17)

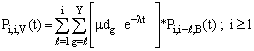(18)

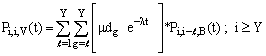(19)

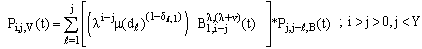(20)

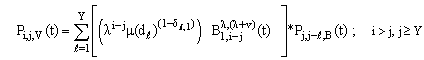(21)

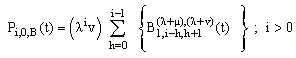(22)

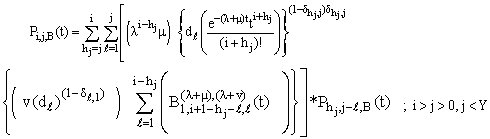(23)

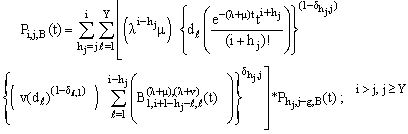(24)

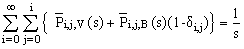From the equations (7) to (15), it is seen that and hence 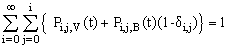a verification.

4. Measures

1. The Laplace transform 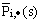of the probability 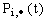that exactly i units arrive by time t can be obtained by using the equations (7) to (15), and is given by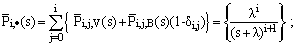

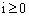and hence

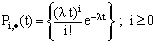The arrivals follow a Poisson distribution as the probability of the total number of arrivals is not affected by the vacation time of the server.

2. The Laplace transform of the mean number of ar-rivals is 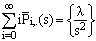and the Laplace inverse of the mean number of arrivals by time t is

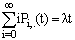3. The departures process from M/M/1 queue has the distribution function, the probability that exactly j customers have been served by time t. In terms of we have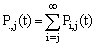

4. The density function of T, the time for the jth de-parture, can be obtained as 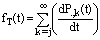Since 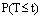= Prob. {atleast j departures in (0,t)} =

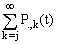5. The probability of exactly n customers in the system at time t, denoted by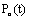, in terms of 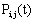as .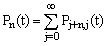

6. The waiting time distribution for a customer can be derived as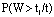, the probability that a customer waits more than 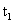time units in the system, given that the customer arrives at time t.

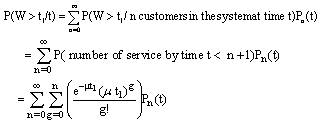7. The system utilization, i.e. the fraction of time the server is busy until time t can also be obtained in terms of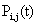. The probability that the system is empty at some time 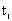is 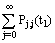. Thus the fraction of the time that the system is empty and consequently the server is idle is 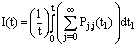and the fraction of time that the system is non-empty and, hence, the server utilized is .

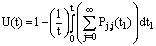5 Conclusions

In this paper we studied two-state multiple vacation queuing model with batch departures. We obtain (i) the probability 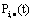of exactly i arrivals by time t, (ii) 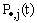the probability that exactly j departures by time t, (iii) the probability of exactly n customers 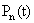in the system at time t, (iv) the waiting time of a customer can also be derived, and (v) system utilization time. So this measure 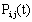is more justified in many practical situations.

6. Particular Cases

1. Results for the case, when departures are occurring one by one, are obtained by substituting 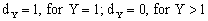in equations (16) to (24).

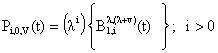(26)

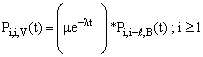(27)

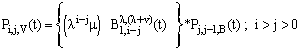(28)

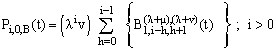(29)

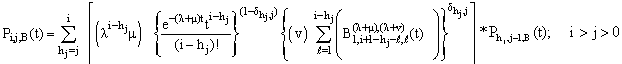(30)

The results (25) to (30) agree with the results (15) to (20) of Indra [24].

6.1. Particular Case of Case-1

1. (a) When the server is instantaneously available, i.e. the mean vacation time is zero. Letting 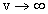in equations (25) to (30), we obtain

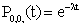(31)

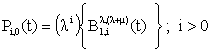(32)

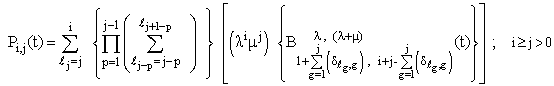(33)

These results (31) to (33) coincide with the results of Pegden and Rosenshine [1].

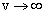2. When the server is instantaneously available, i.e. by letting in equations (16) to (24), we have

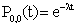(34)

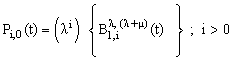(35)

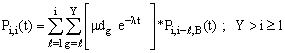(36)

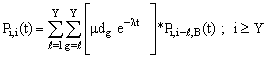(37)

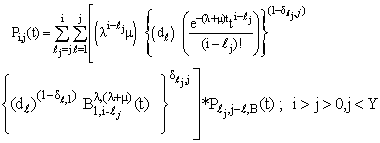(38)

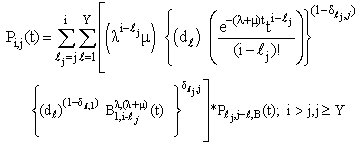(39)

The results (34) to (39) coincide with the results (1.3A.13) to (1.3A.15) of Prem Chand [27].

ACKNOWLEDGEMENTS

One of the authors is grateful to Vice Chancellor of NIFTEM for providing necessary facilities.