-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2013; 3(A): 17-25
doi:10.5923/s.ajor.201305.03
Finite Queueing Model with Multitask Servers and Blocking
Chandra Shekhar 1, Madhu Jain 2
1Department of Mathematics, Birla Institute of Technology and Science, Pilani Campus, Pilani, Rajasthan, 333 031, India
2Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee, Uttarakhand, 247 667, India
Correspondence to: Chandra Shekhar , Department of Mathematics, Birla Institute of Technology and Science, Pilani Campus, Pilani, Rajasthan, 333 031, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper deals with a Markovian queueing system having a multi-task service counters and finite queue in front of each counter. The total service of a customer is completed in three stages provided by two servers at three counters. The first server (S1) can serve the counter I and III alternatively, whereas second server (S2) provides the service at counter II. The server (S1) gives the priority to the customers waiting for stage third for the service at counter III since they are in last phase of service completion. The steady state queue size distribution has been obtained. The expressions for mean number of customers in the system, average queue length and blocking probability have been obtained. Sensitivity analysis has been carried out to study the effect of variation of different parameters.
Keywords: Queue, Tandem, Multi-task, Markov Process, Queue Size Distribution, Blocking Probability
Cite this paper: Chandra Shekhar , Madhu Jain , Finite Queueing Model with Multitask Servers and Blocking, American Journal of Operational Research, Vol. 3 No. A, 2013, pp. 17-25. doi: 10.5923/s.ajor.201305.03.
Article Outline
1. Introduction
- Queueing theory has been widely used to model various service systems to provide Quality of Service (QoS) dealing with many congestion situations of day – to - day life. Queueing situations at any service station provide a variety of fascinated challenges to the mathematicians who are interested in applications of probability theory and optimization. Question of interest in the design of optimal service system is to predict the average delay at various interacting and sequenced counters managed by multitask servers and by incorporating customer’s behaviour. In such a system formation of tandem queues, blocking is very common. Tandem queues with blocking have been addressed by many theorists and researchers. Optimal ordering of stations in tandem queue with blocking was considered by Ding and Greenberg[1]. Altiok[2], Altiok and Perros[3], Brandwajn and Jow[4] developed algorithms which can be used for the analysis of tandem networks with exponential service times and Poisson external arrivals. Morris and Perros[5] presented a discrete-time tandem network of cut-through queues and introduced a new bursty arrival process. They analyzed the tandem network using single-node decomposition. Charles and LaPadula[6] analyzed the performance of multi-queue single-server systems consisting of many queues. They approximated polling system consisting of several queues. The explicit time – dependent distribution of the number of tasks for a parallel multi-processor system with task-splitting and feedback was obtained by Haghighi[7]. Zhang and Tian[8] studied a Markovian queueing system with multi-task servers where each server can perform two types of job. Using the matrix analytic method, they provided a new computational algorithm for the stationary distributions of the queue length and waiting time. The analysis of networks of queues under repetitive service blocking mechanism had been presented by Awan et al.[9]. They assumed that the nodes are connected according to an arbitrary configuration and each node in the networks employs an active queue management (AQM) based queueing policy to guarantee certain quality of service for multiple class external traffic. Bhaskar and Lallement[10] investigated supply chain which is represented as a two-input, three-stage queueing network. They computed the minimum response time for the delivery of items to the final destination along the three stages of the network. Yang et al.[11] considered a finite capacity M/M/R queue with second optional channel. Using the matrix - geometric method, they obtained the steady-state probability distributions and various system performance measures.Intermediate buffer space plays a very important role in managing tandem queues which arise due to variation in service facility at different counters. Kavusturucu and Gupta[12] modeled finite buffer tandem manufacturing system under N policy using open queueing networks. They computed the throughput of the system using decomposition, isolation and expansion methodologies. Vidalis and Papadopoulos[13] obtained the exact solution of the large sparse linear system by the use of the Gauss–Seidel method for reliable multi-station series queueing networks where buffers of non-identical finite capacities are allowed between successive stations. Aweya et al.[14] proposed a new active queue management scheme for a network device (e.g. router, switch, etc.) with a shared buffer where the buffer is logically organized into multiple queues. Sharma and Virtamo[15] considered a queue with finite buffer where the buffer size limits the amount of work that can be stored in the queue. They obtained the stability, the rates of convergence to the stationary distribution and functional limit theorems for this system. In addition, they also obtained algorithms to compute the stationary density of the workload process, the waiting times and the probability of packet loss. Chydzinski and Winiarczyk[16] investigated the blocking probability in a finite–buffer queue whose arrival process is given by the batch Markovian arrival process. Using the supplementary variable and imbedded Markov chain techniques, Goswami et al.[17] obtained the queue-length distributions at pre-arrival and arbitrary epochs for finite - buffer multi - server bulk - service queueing system. Diamantidis and Papadopoulos[18] used exact Markovian analysis to examine the model of a serial flow line with two workstations and an intermediate buffer where each workstation has multiple unreliable and non-identical parallel machines.The behavior of the customer in the queue is very important factor for analyzing the quality of service in any service system. Wang et al.[19] developed profit model to determine the optimal number of servers in the system under the constraint of impatience behaviors of the customers. Yang and Choo[20] considered an M/M/s queue with balking, reneging and retrials. They developed an algorithm for the stationary distribution of the Markov chain and presented some numerical results. Al-Seedy et al.[21] used generating function technique to obtain the transient solution for the M/M/c queue with balking and reneging. Perel and Yechiali[22] studied M/M/c queues (c=1,
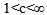 and
and 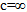 ) in a two-phase (fast and slow) Markovian random environment, with impatient customers. Recently there has been considerable interest in state dependent queueing models. In real life situations, the customer’s behaviour may play a deciding role on the service rate of a server. The input traffic may also be influenced by the status of the servers. In the last few years, researches on queueing network theory have been redirected by a series of brilliant and sobering examples. Queues with state dependent arrival rate have wide applications in computers and communication system, production processes, etc. Shagon[23] studied a single server queueing model wherein arrival rate depends on the server status. Using approximation for the general service time distribution by phase type distribution, M/G/1 queue with queue length dependent arrival rate was investigated by Gong et al.[24]. A state dependent queueing model wherein the service rate is adjusted at the beginning of service was studied by Wang[25]. Jain[26] studied optimal N-policy for state dependent Markovian queue with single removable and unreliable server. Hwang et al.[27] proposed a Markov decision theoretic frame-work for a multi-rate network by approximating a single state-dependent Poisson arrival stream without incurring any significant increase in computational complexity. Jain et al.[28] analyzed the finite queue-dependent heterogeneous multiprocessor service system in which processors are shared by more than one job. They obtained steady-state queue size distribution using recursive method considering Markovian arrival and service times. Lee and Kim[29] considered an M/G/1 queueing system where the speed of the server depends on the amount of work present in the system. By using the level crossing theory and solving the corresponding integral equation, they obtained the stationary distribution of the workload in the system in explicit form. For a single-server retrial queue with state dependent exponential inter-arrival, service and inter-retrial times, Parthasarathy and Sudesh[30] studied the time dependent system size probabilities by employing the continued fractions. Wall and Worthington[31] considered the time dependent behavior of virtual waiting time for modeling of approximate time dependent behavior of queue length of the form M(t)/G/c queueing model. Soares and Latouche[32] developed various models of fluid queues with a level dependency component where the behavior of the phase process changes when the level crosses certain thresholds, as well as the rate at which fluid increases or decreases. Banik[33] considered an infinite-buffer single - server queue with renewal input. Lee[34] considered a class of stochastic networks with state-dependent arrival and service rates. Under the uniform (in state) stability condition, he established several moment stability properties of the system. Banerjee and Gupta[35] analyzed single-server finite-buffer queue where customers arrive according to Poisson process and served in batches of minimum size and maximum threshold limit. Louvel et al.[36] recently presented a non - intrusive and adaptable resource management framework which was developed upon a customized architecture. Zhou et al.[37] gave exact analysis of two-stage tandem queueing network with MAP inputs and buffer sharing using matrix filtration technique. MAP/M/2 queueing system in steady - state was analyzed by Chakravarthy and Karatz[38] with two identical servers in parallel system and pure space sharing among rigid jobs using matrix analytic method.In this paper we deal with Markovian queueing system wherein jobs are served by two multi-task servers at three counters. The input traffic is assumed to be effected by the status of the server. The state-dependent server may provide service with faster rate to reduce the backlog in case of long queue. The organization of the paper is as follows. The description of the model and underlying assumptions and notations are given in section 2. In section 3 governing equations and queue size distribution are established. The expressions for mean number of jobs in the system and blocking probability are obtained in section 4. The numerical algorithm to develop a computer program is discussed in section 5. Numerical illustrations and sensitivity analysis are also provided. Concluding remarks and scopes of future work are given in the last section 6.
) in a two-phase (fast and slow) Markovian random environment, with impatient customers. Recently there has been considerable interest in state dependent queueing models. In real life situations, the customer’s behaviour may play a deciding role on the service rate of a server. The input traffic may also be influenced by the status of the servers. In the last few years, researches on queueing network theory have been redirected by a series of brilliant and sobering examples. Queues with state dependent arrival rate have wide applications in computers and communication system, production processes, etc. Shagon[23] studied a single server queueing model wherein arrival rate depends on the server status. Using approximation for the general service time distribution by phase type distribution, M/G/1 queue with queue length dependent arrival rate was investigated by Gong et al.[24]. A state dependent queueing model wherein the service rate is adjusted at the beginning of service was studied by Wang[25]. Jain[26] studied optimal N-policy for state dependent Markovian queue with single removable and unreliable server. Hwang et al.[27] proposed a Markov decision theoretic frame-work for a multi-rate network by approximating a single state-dependent Poisson arrival stream without incurring any significant increase in computational complexity. Jain et al.[28] analyzed the finite queue-dependent heterogeneous multiprocessor service system in which processors are shared by more than one job. They obtained steady-state queue size distribution using recursive method considering Markovian arrival and service times. Lee and Kim[29] considered an M/G/1 queueing system where the speed of the server depends on the amount of work present in the system. By using the level crossing theory and solving the corresponding integral equation, they obtained the stationary distribution of the workload in the system in explicit form. For a single-server retrial queue with state dependent exponential inter-arrival, service and inter-retrial times, Parthasarathy and Sudesh[30] studied the time dependent system size probabilities by employing the continued fractions. Wall and Worthington[31] considered the time dependent behavior of virtual waiting time for modeling of approximate time dependent behavior of queue length of the form M(t)/G/c queueing model. Soares and Latouche[32] developed various models of fluid queues with a level dependency component where the behavior of the phase process changes when the level crosses certain thresholds, as well as the rate at which fluid increases or decreases. Banik[33] considered an infinite-buffer single - server queue with renewal input. Lee[34] considered a class of stochastic networks with state-dependent arrival and service rates. Under the uniform (in state) stability condition, he established several moment stability properties of the system. Banerjee and Gupta[35] analyzed single-server finite-buffer queue where customers arrive according to Poisson process and served in batches of minimum size and maximum threshold limit. Louvel et al.[36] recently presented a non - intrusive and adaptable resource management framework which was developed upon a customized architecture. Zhou et al.[37] gave exact analysis of two-stage tandem queueing network with MAP inputs and buffer sharing using matrix filtration technique. MAP/M/2 queueing system in steady - state was analyzed by Chakravarthy and Karatz[38] with two identical servers in parallel system and pure space sharing among rigid jobs using matrix analytic method.In this paper we deal with Markovian queueing system wherein jobs are served by two multi-task servers at three counters. The input traffic is assumed to be effected by the status of the server. The state-dependent server may provide service with faster rate to reduce the backlog in case of long queue. The organization of the paper is as follows. The description of the model and underlying assumptions and notations are given in section 2. In section 3 governing equations and queue size distribution are established. The expressions for mean number of jobs in the system and blocking probability are obtained in section 4. The numerical algorithm to develop a computer program is discussed in section 5. Numerical illustrations and sensitivity analysis are also provided. Concluding remarks and scopes of future work are given in the last section 6. 2. System Description
 | Figure 1. Three counters service system with two servers |
 The jobs are independent to each other.• The arriving jobs may balk only at counter 1 with probability
The jobs are independent to each other.• The arriving jobs may balk only at counter 1 with probability 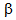 (0<
(0<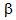 <1) when queue size reaches to a threshold value N1 (N1>1).• The job entering in the system has to be served by all (three) counters i.e. the jobs form tandem queue. It is not allowed to leave in between without getting complete service. The flow of jobs in the service facility is shown in the figure 1. • Counters I and III are operated by the first server (S1) whereas second server (S2) operates single counter II. Both servers are independent to each others.• The service times at counters I, II, and III are exponential distributed with rates
<1) when queue size reaches to a threshold value N1 (N1>1).• The job entering in the system has to be served by all (three) counters i.e. the jobs form tandem queue. It is not allowed to leave in between without getting complete service. The flow of jobs in the service facility is shown in the figure 1. • Counters I and III are operated by the first server (S1) whereas second server (S2) operates single counter II. Both servers are independent to each others.• The service times at counters I, II, and III are exponential distributed with rates 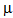 1,
1, 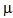 2, and
2, and 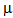 3, respectively. The state-dependent servers at counter II and III switch to faster rate
3, respectively. The state-dependent servers at counter II and III switch to faster rate 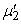 and
and 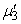 respectively, if there are more than N2 (N2>1) jobs at counter II and at least one job at counter I respectively.• The discipline for service at all counters is First Come First Served (FCFS). • The queue is allowed to be formed in front of each counter within the buffer and waiting space capacity of system i.e. at most M jobs are allowed in the system.• The times taken for transaction of jobs between counters in sequence are assumed to be negligible.• The switching time of first server (S1) between counter I and counter III is also negligible. The following notations are used for mathematical formulation of birth-death process:P0,0,0 Steady-state probability that the system is idle i.e. there is no job at any counter.Pi,j,k Steady-state probability that there are i, j and k jobs at counters I, II, and III respectively, for service. PI Fraction of time during which the server (S1) is busy at counter I.PIII Fraction of time during which the server (S1) is busy at counter III.
respectively, if there are more than N2 (N2>1) jobs at counter II and at least one job at counter I respectively.• The discipline for service at all counters is First Come First Served (FCFS). • The queue is allowed to be formed in front of each counter within the buffer and waiting space capacity of system i.e. at most M jobs are allowed in the system.• The times taken for transaction of jobs between counters in sequence are assumed to be negligible.• The switching time of first server (S1) between counter I and counter III is also negligible. The following notations are used for mathematical formulation of birth-death process:P0,0,0 Steady-state probability that the system is idle i.e. there is no job at any counter.Pi,j,k Steady-state probability that there are i, j and k jobs at counters I, II, and III respectively, for service. PI Fraction of time during which the server (S1) is busy at counter I.PIII Fraction of time during which the server (S1) is busy at counter III.3. Mathematical Analysis
- The steady-state Chapman-Kolmogrov differential difference equations governing the present model are as follows:
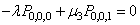 | (1) |
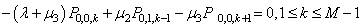 | (2) |
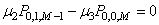 | (3) |
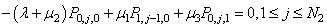 | (4) |
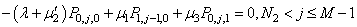 | (5) |
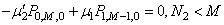 | (6) |
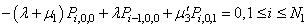 | (7) |
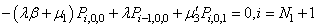 | (8) |
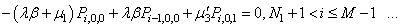 | (9) |
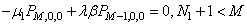 | (10) |
 | (11) |
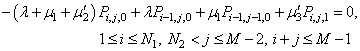 | (12) |
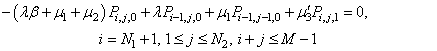 | (13) |
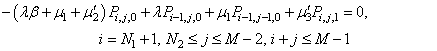 | (14) |
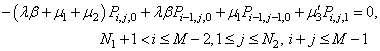 | (15) |
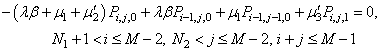 | (16) |
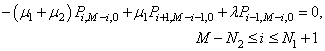 | (17) |
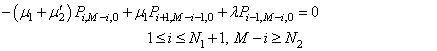 | (18) |
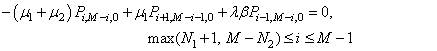 | (19) |
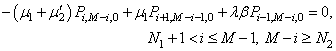 | (20) |
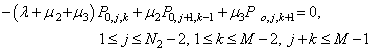 | (21) |
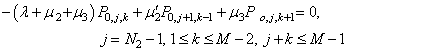 | (22) |
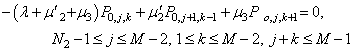 | (23) |
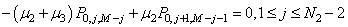 | (24) |
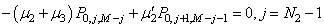 | (25) |
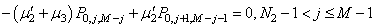 | (26) |
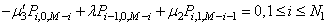 | (27) |
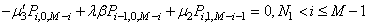 | (28) |
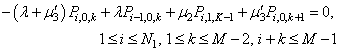 | (29) |
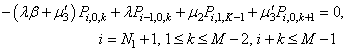 | (30) |
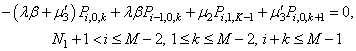 | (31) |
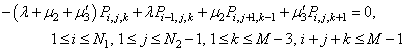 | (32) |
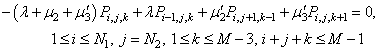 | (33) |
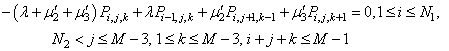 | (34) |
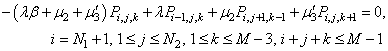 | (35) |
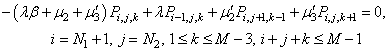 | (36) |
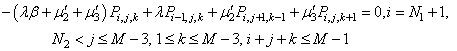 | (37) |
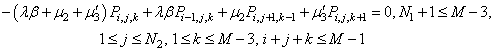 | (38) |
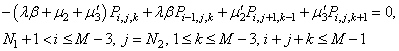 | (39) |
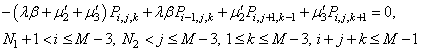 | (40) |
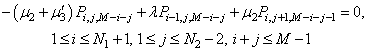 | (41) |
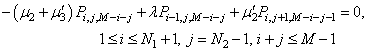 | (42) |
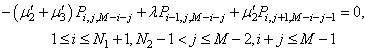 | (43) |
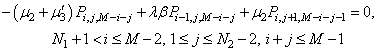 | (44) |
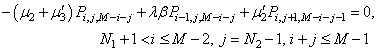 | (45) |
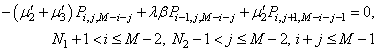 | (46) |
 | (47) |
 | (48) |
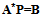 | (49) |
4. The System Performance Measures
- For queueing model under consideration, using the steady-state probabilities derived in the previous section, we compute following system performance measures: (i) The mean number of jobs in the system (L) is
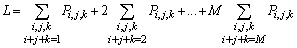 | (50) |
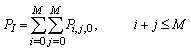 | (51) |
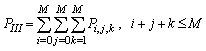 | (52) |
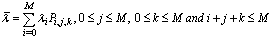 | .(53) |
 .
.5. Numerical Results
- In order to validate the computational tractability, the performance measures established above have been used to generate numerical results. The computer program is developed in software package MATLAB by writing code to compute performance measures. The average number of jobs in the system and blocking probabilities are obtained numerically by varying various parameters and are summarized in Tables 1, 2, and 3.
|
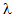 from 0.1 to 1.0 for different room capacity (M). The service rates at different counter are fixed as
from 0.1 to 1.0 for different room capacity (M). The service rates at different counter are fixed as 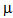 1 = 1.1,
1 = 1.1, 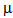 2 = 0.8,
2 = 0.8, 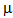 3 = 1.2. The threshold parameters N1 and N2 for balking are fixed at 5 and the balking rate (
3 = 1.2. The threshold parameters N1 and N2 for balking are fixed at 5 and the balking rate (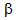 is 0.8. The value of faster service rates at counter II and III are
is 0.8. The value of faster service rates at counter II and III are 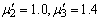 respectively. A significant increasing trend are observed in all performance measures L, PI, PIII with respect to room capacity (M) and arrival rate (
respectively. A significant increasing trend are observed in all performance measures L, PI, PIII with respect to room capacity (M) and arrival rate (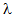 ) which is true in realistic situation.
) which is true in realistic situation.
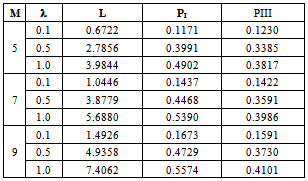
|
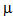 1=1.1
1=1.1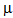 ,
, 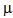 2=0.8
2=0.8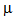 ,
, 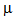 3=1.2
3=1.2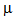 . The value of
. The value of 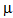 is varying from 1 to 2. The changed service rate for counter II and III are
is varying from 1 to 2. The changed service rate for counter II and III are 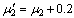 and
and 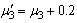 . The arrival rate chosen is
. The arrival rate chosen is 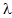 =0.5. All others parameters are same as in Table 1. An average number of jobs in the system and blocking probabilities are exhibiting decreasing trend with respect to service rate.
=0.5. All others parameters are same as in Table 1. An average number of jobs in the system and blocking probabilities are exhibiting decreasing trend with respect to service rate.
|
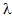 =0.5. All other parameters are same as in Table 1. A prominent decreasing effect is observed in the value of performance measures for higher room capacity with respect to balking probability.In Figures 2(a)-2(d) the variation of average number of jobs in system is displayed by varying
=0.5. All other parameters are same as in Table 1. A prominent decreasing effect is observed in the value of performance measures for higher room capacity with respect to balking probability.In Figures 2(a)-2(d) the variation of average number of jobs in system is displayed by varying 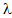 ,
, 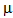 , M, and
, M, and 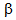 respectively. The average number of jobs increases with the increase in arrival rate (
respectively. The average number of jobs increases with the increase in arrival rate (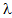 and room capacity (M) which matches with physical situation. By increasing service rate (
and room capacity (M) which matches with physical situation. By increasing service rate (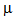 and balking probability (
and balking probability (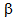 , the average number of jobs reduces but the effect of
, the average number of jobs reduces but the effect of 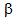 is negligible for small room capacity.These figures exhibit realistic result. Hence, the system designer should provide the efficient servers in service system to check reluctance behavior among customers which directly or indirectly affect on average number of jobs in the system. The present study shows that system capacity is important parameter for timeliness and efficient service. The decision maker should analyze the system’s size efficiently since it directly affect service cost and customer’s satisfactions.
is negligible for small room capacity.These figures exhibit realistic result. Hence, the system designer should provide the efficient servers in service system to check reluctance behavior among customers which directly or indirectly affect on average number of jobs in the system. The present study shows that system capacity is important parameter for timeliness and efficient service. The decision maker should analyze the system’s size efficiently since it directly affect service cost and customer’s satisfactions.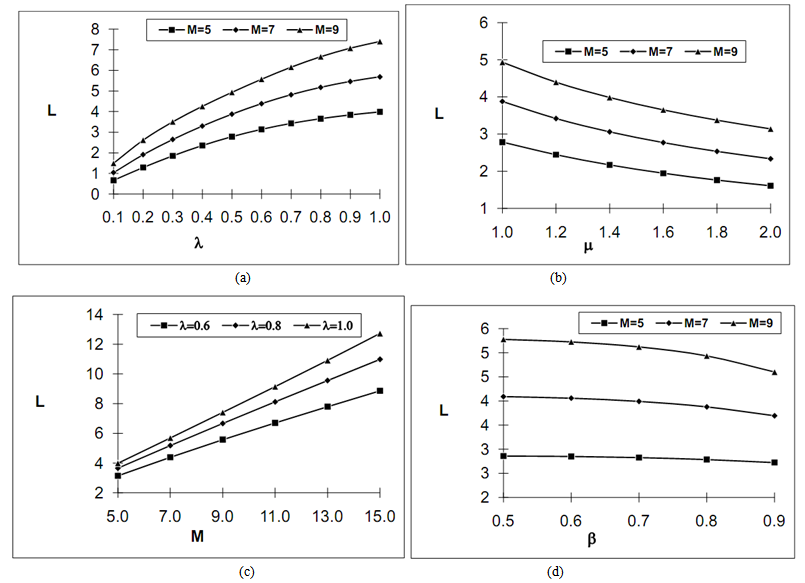 | Figure 2. Number of jobs in the system |
6. Conclusions
- In this paper we have studied the multi-tasking server that oscillates between counters with balking and state-dependent service rate. The service of job is done through three counters. Numerical solution is obtained using matrix method. The performance of the system is measured in terms of average waiting time in the system, average number of jobs in the system and blocking probabilities for different arrival rate, service rate and balking rate. The state dependent rate incorporated for modelling multi-counters system make our results more closer to realistic situation. The system analyst can analyze such model by incorporating associated cost factors and optimize the time fraction between counters and service rates of the servers. However there is scope of extension of this work by considering bulk arrivals and/or bulk service in which direction the attention should be paid. We should go for the transient solution to make our model more realistic. We can analyze present model under shadow of various type of server’s policies and customer’s policies. We can extend our model for other different kind of architectural restrictions.
ACKNOWLEDGEMENTS
- The authors would like to thank the anonymous referees and the Editor-in-Chief of the Journal for their valuable suggestions and critical comments which help a lot in improving the quality and clarity of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML and M (for
and M (for 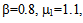
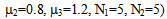
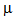 and M (for
and M (for 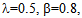
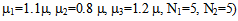
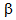 and M (for
and M (for