-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2013; 3(A): 7-16
doi:10.5923/s.ajor.201305.02
An M/G/1 Retrial Queue with a Single Vacation Scheme and General Retrial Times
K. Lakshmi1, Kasturi Ramanath2
1Department of Mathematics, A.M. Jain College, Meeambakkam, Chennai-114, Tamil Nadu, India
2School of Mathematics, Madurai Kamaraj University, Madurai-21, Tamil Nadu, India
Correspondence to: K. Lakshmi, Department of Mathematics, A.M. Jain College, Meeambakkam, Chennai-114, Tamil Nadu, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Let us consider a service facility where a single server provides some service. It could be a plumber looking after repair and maintenance of the plumbing work in the apartment complexes situated near the shop or could be an electrician or a painter. Requests for service arrive in accordance with a Poisson process. When the server is away with the service of a customer, any other requests for service can be recorded and the customer cannot wait in a queue but has to leave and try for service after some time. The server after completion of the work on hand decides to take a break before attending to the next chore. This is an example of a retrial queue in which the server takes a vacation after the completion of each service. Motivated by this example, we have studied an M/G/1 retrial queue with server vacations. In this paper, we assume that the retrial times are generally distributed and that the retrial policy is constant. We have derived probability generating functions of the system size and the orbit size. We have investigated the conditions under which the steady state exists. Some useful performance measures are also obtained. Numerical examples are provided to illustrate the sensitivity of the performance measures to changes in the parameters of the system.
Keywords: Retrial Queues,Constant Retrial Policy, Single Vacations, Steady StateBehaviour
Cite this paper: K. Lakshmi, Kasturi Ramanath, An M/G/1 Retrial Queue with a Single Vacation Scheme and General Retrial Times, American Journal of Operational Research, Vol. 3 No. A, 2013, pp. 7-16. doi: 10.5923/s.ajor.201305.02.
Article Outline
1. Introduction
- In this paper, we consider a single-server retrial queue with server vacations. We have assumed that the inter-retrial times are generally distributed with a constant retrial policy. After the completion of each service the server goes on a vacation of random length. After the completion of each vacation, the server waits for the next customer. This could be either a primary arrival or the server could try to contact the first customer in the orbit. This is in contrast to the multiple vacation schemes, where the server could take a vacation every time he finds no customers in the system.An example of such a retrial queuing system is as follows; a service provider (plumber, painter, electrician etc.,) is provided with some mechanism to record the details of the customers requesting service, when he is away attending to some job. After the completion of each service, the provider may take a break before going back to attend to the next customer. Customer requests which arrive during his absence do not wait in a queue but after recording their requirements go away to come back after some time to repeat the request for service.Motivated by this example, we have therefore considered a retrial queue with a limited single vacation scheme. This scheme is different from the one based on the Bernoulli schedule vacations and applied in the literature by authors like Wang and Li[15], Ebenesar Anna Bagyam and Udaya Chandrika[10]. The rest of the paper is organized as follows: In section-2, we present a brief review of related works in the queueing theory literature. In Sec-3; we present the mathematical model of the system. In Sec-4, we present a steady state analysis of the system and we derive the joint probability generating functions (P.G.F’s) of the server state and orbit size and server state and system size. In Sec-5, we derive the necessary and sufficient condition for the existence of the steady state. In sec-6, we consider some useful performance measures of the system. In Sec-7, numerical results are used to compare numerically the system performance measures with respect to changes of parameters.
2. Literature Review
- Retrial queueing systems form an active research area due to their wide applicability in telephone switching system, telecommunication networks and computer networks. Retrial queueing systems are those systems in which arriving customers, who find the server busy, join the retrial queue (orbit) to try again for their requests after sometime. Retrial queues are useful in modeling many problems in telephone switching systems, computer and communication systems. A review of the literature on retrial queues and their applications can be found in Falin[11] and Yang and Templeton[23], and Artalejo[6]. Two monographs entirely derived to the topic exist and are written by Falin and Templeton[12] and Artalejo and Gomez-Correl[5].In retrial queueing literature, retrial customers are usually assumed to behave independently and return without regard to other retrial customers. However, Farahmand[13] proposed a special type of retrial system with FCFS retrial queue, that is, if a customer finds the server busy, he may join the tail of a retrial queue in accordance with a first-come-first-served (FCFS) discipline and the customer at the head of the retrial queue would then try again to enter the system, competing with new arrivals. Gomez-Corral[14] considered an M/G/1 retrial queue with a FCFS retrial queue and general retrial times. Single-server queues with vacations have been studied extensively in the past. Comprehensive surveys can be found in Doshi[9] and Takagi[22] and recent developments in vacation queueing Models was introduced by Ke et.al[16], Krishnakumar and Arivudainambi[17]. In our model the server takes a break every time he completes the service. Most of the analyses for retrial queues with vacations concern the exhaustive service schedule (Artalejo[1] and Artalejo and Rodrigo[4]) and the gated service policy (Langaris[20]).Recently, several authors considered retrial queues with Bernoulli schedule, as can be seen in Atencia and Moreno[7], Kumar et al.[18] and Zhou[24]. In this paper we have considered a limited vacation policy. Kasturi Ramanath and K.Kalidass[19] have considered a two phase service M/G/1 vacation queue with general retrial times and non-persistent customers.In the context of the service provider the limited vacation scheme wherein, the server takes the vacation after each service completion is appropriate. Also, the server cannot take a vacation each time he finds the system empty. The FCFS orbit also makes sense since the server has a record of all the requests that have arrived during his absence. With these ideas we have included a FCFS orbit, a limited single vacation scheme into our model.
3. The Mathematical Model
- In this section, we consider a Single-server retrial queuing system with a non-exponential retrial time distribution and with server vacations. Arriving customers to the system are in accordance with a Poisson process with a rate
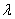 . The service time is generally distributed with a distribution function B(x), Laplace Stieljes transform (LST)
. The service time is generally distributed with a distribution function B(x), Laplace Stieljes transform (LST) 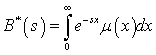 and the hazard rate function
and the hazard rate function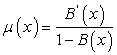 .A customer upon arrival, who finds the server free, immediately proceeds for service. Otherwise, the customer leaves the system and joins an orbit from where he/she makes repeated attempts to gain service. The time intervals between two successive retrials are assumed to be generally distributed with a distribution function R(x), hazard rate function
.A customer upon arrival, who finds the server free, immediately proceeds for service. Otherwise, the customer leaves the system and joins an orbit from where he/she makes repeated attempts to gain service. The time intervals between two successive retrials are assumed to be generally distributed with a distribution function R(x), hazard rate function  and LST R*(s).We assume that only the customer at the head of the orbit is allowed to make repeated attempts.We also assume that the elapsed retrial time is measured from the moment the server becomes available for service.After completion of a service, the server is allowed to take a vacation. The duration of the server vacation is assumed to be generally distributed with a distribution function V(x), a LST V*(s) and a hazard rate function
and LST R*(s).We assume that only the customer at the head of the orbit is allowed to make repeated attempts.We also assume that the elapsed retrial time is measured from the moment the server becomes available for service.After completion of a service, the server is allowed to take a vacation. The duration of the server vacation is assumed to be generally distributed with a distribution function V(x), a LST V*(s) and a hazard rate function 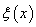 .We assume that the inter-arrival times, service times, inter-retrial times and the duration of the server vacation are all independent of each other.Let N (t) denote the number of customers in the orbit at any instant of time t. Let C (t) denote the state of the server at time t:
.We assume that the inter-arrival times, service times, inter-retrial times and the duration of the server vacation are all independent of each other.Let N (t) denote the number of customers in the orbit at any instant of time t. Let C (t) denote the state of the server at time t: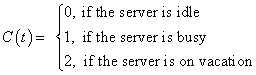 In order to make the stochastic process involve into a continuous time Markov process, we employ the supplementary variable technique. This was first introduced by Cox[7]. See Medhi[21] for a detailed explanation of the technique.We define the supplementary variable X (t) as follows:
In order to make the stochastic process involve into a continuous time Markov process, we employ the supplementary variable technique. This was first introduced by Cox[7]. See Medhi[21] for a detailed explanation of the technique.We define the supplementary variable X (t) as follows: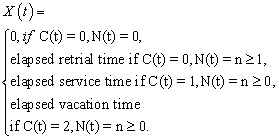 We define the following probability functions:
We define the following probability functions: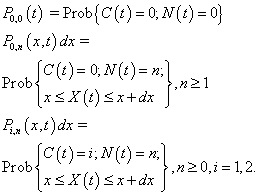 Then
Then 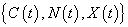 is a continuous time Markov process.
is a continuous time Markov process.4. Steady State Analysis
- Now, analysis of our queueing model can be performed with the help of the following Kolmogorov forward equations:
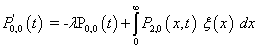 | (1) |
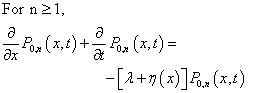 | (2) |
 | (3) |
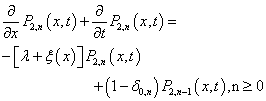 | (4) |
 ,
,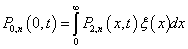 | (5) |
 | (6) |
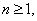
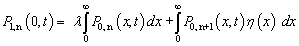 | (7) |
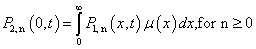 | (8) |
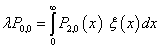 | (9) |
 | (10) |
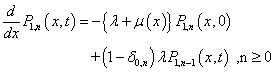 | (11) |
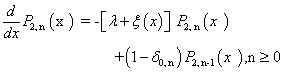 | (12) |
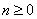 ,
,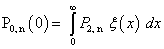 | (13) |
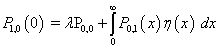 | (14) |
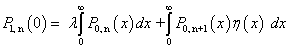 | (15) |
 | (16) |
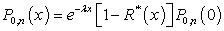 We define the following partial probability generating functions, for
We define the following partial probability generating functions, for 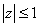 ,
,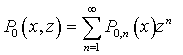 | (17) |
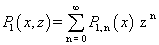 | (18) |
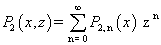 | (19) |
 | (20) |
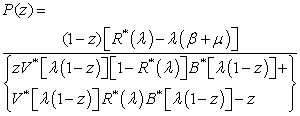 | (21) |
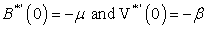 and the probability generating function of the system size is given by
and the probability generating function of the system size is given by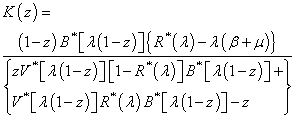 | (22) |
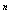 and summing over n from 0 to
and summing over n from 0 to 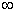 , the solution of the resulting equation is
, the solution of the resulting equation is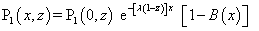 | (23) |
 | (24) |
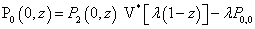 | (25) |
 | (26) |
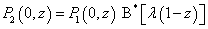 | (27) |
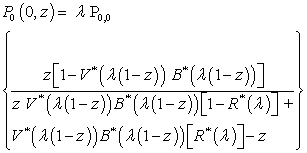 | (28) |
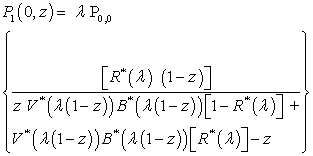 | (29) |
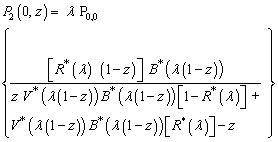 | (30) |
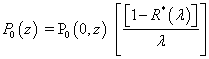 | (31) |
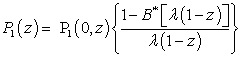 | (32) |
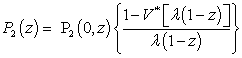 | (33) |
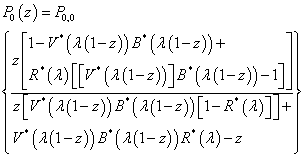 | (34) |
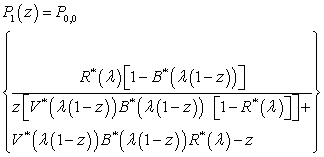 | (35) |
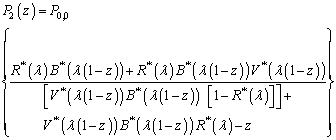 | (36) |
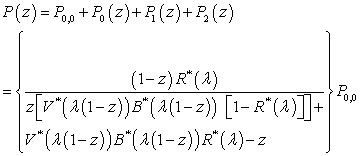 | (37) |
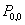 , we use the normalizing condition P (1) =1.Applying L’Hospital’s rule in an appropriate place we get
, we use the normalizing condition P (1) =1.Applying L’Hospital’s rule in an appropriate place we get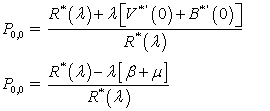 | (38) |

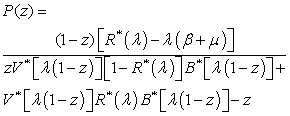 | (39) |

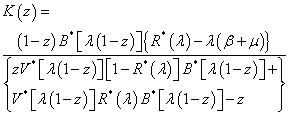 | (40) |
5. The Embedded Markov Chain
- In this section, we derive the necessary and sufficient condition for stability of our system. We consider the embedded Markov chain of the process.Let
 be the number of customers in the orbit immediately after the
be the number of customers in the orbit immediately after the 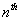 service completion epoch
service completion epoch 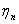 . Then
. Then 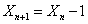 if the
if the 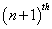 customer is a retrial customer, otherwise
customer is a retrial customer, otherwise 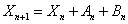 , where
, where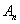 is the number of arrivals into the orbit during the vacation time of the server and
is the number of arrivals into the orbit during the vacation time of the server and  is the number of customers arriving into the orbit during the service time of the
is the number of customers arriving into the orbit during the service time of the 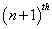 customer.By our assumption, the arrival process is independent of the service mechanism and of the vacations of the server and of the retrial processes initiated by the customers in the orbit. Therefore
customer.By our assumption, the arrival process is independent of the service mechanism and of the vacations of the server and of the retrial processes initiated by the customers in the orbit. Therefore 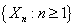 is a Markov chain. The system is ergodic if and only if the embedded Markov chain
is a Markov chain. The system is ergodic if and only if the embedded Markov chain 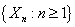 is ergodic. To prove that the embedded Markov chain is ergodic,we employ Foster’s criterion whose statement is given below:Foster’s criterion: For an irreducible and aperiodic Markov chain
is ergodic. To prove that the embedded Markov chain is ergodic,we employ Foster’s criterion whose statement is given below:Foster’s criterion: For an irreducible and aperiodic Markov chain 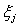 with state space S, a sufficient condition for ergodocity is the existence of a non-negative function f(s),
with state space S, a sufficient condition for ergodocity is the existence of a non-negative function f(s), 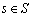 and
and 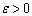 such that the mean drift
such that the mean drift 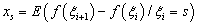 is finite for all and
is finite for all and  for all
for all 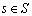 except perhaps a finite number.Theorem 5.1: The necessary and sufficient condition for the system considered in the previous section to be ergodic is given by
except perhaps a finite number.Theorem 5.1: The necessary and sufficient condition for the system considered in the previous section to be ergodic is given by 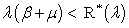 .
.6. Performance Measures
- In this section, we examine some useful performance measures of the system.(a) The expected number of customers in the system is given by
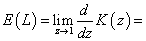
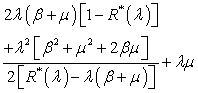 (b) The expected number of customers in the orbit
(b) The expected number of customers in the orbit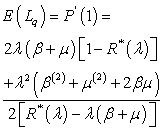 The steady state distribution of the server state is given by
The steady state distribution of the server state is given by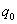 =Prob {server is idle} =
=Prob {server is idle} =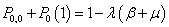 .
.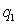 =Prob {server is busy} =
=Prob {server is busy} =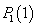 =
=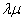 .
. =Prob {server is on vacation} =
=Prob {server is on vacation} = 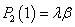 .
.7. Numerical Illustrations
- In order to verify the efficiency of our analytical results, we perform numerical experiments by using MAPLE. In this section, we present some numerical examples to illustrate the effect of varying the parameters on the following performance characteristics of our system. We consider the performance measures: the probabilities q0, q1, q2 are the probabilities of the server being idle, the busy and on vacation respectively. We also consider the expected number of customers in the orbit, expected number of customers in the system and
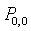 . Moreover, for the purpose of numerical illustrations, we assume that the arrival process is Poisson with parameter
. Moreover, for the purpose of numerical illustrations, we assume that the arrival process is Poisson with parameter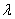 varying from 0.1 to 0.7, the service time distribution function is exponential with mean
varying from 0.1 to 0.7, the service time distribution function is exponential with mean 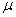 = 0.3, the retrial times follow an exponential distribution with LST
= 0.3, the retrial times follow an exponential distribution with LST 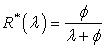 with parameter
with parameter 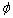 =0.8.The vacation time is also exponentially distributed with mean
=0.8.The vacation time is also exponentially distributed with mean 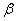 = 0.25.In all the cases, the parametric values are chosen to satisfy the stability condition.Example 1: In this example, we study the effect of varying the arrival rate λ.From table 1, we observe that if the value of
= 0.25.In all the cases, the parametric values are chosen to satisfy the stability condition.Example 1: In this example, we study the effect of varying the arrival rate λ.From table 1, we observe that if the value of 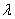 increases, the probabilities of idle time-
increases, the probabilities of idle time- and
and  decrease. The probabilities of busy time, expected no. of customers in the system and the expected no. of customers in the orbit also increase.The graph for the data given in table 1 is given below;
decrease. The probabilities of busy time, expected no. of customers in the system and the expected no. of customers in the orbit also increase.The graph for the data given in table 1 is given below;
|
 | Figure 1. Effect of varying λ on various performance measures |
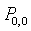 (i.e.) the probability of no customers in the system and the server is idle decreases with increasing values of
(i.e.) the probability of no customers in the system and the server is idle decreases with increasing values of 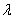 . Similarly, Fig(1.2) shows how the proportion of idle time of the server decreases with increasing values of
. Similarly, Fig(1.2) shows how the proportion of idle time of the server decreases with increasing values of 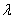 . Fig (1.3), Fig (1.4), Fig (1.5) and Fig (1.6) show how the server’s busy period and vacation period probabilities, the expected number of customers in the system and the expected number of customers in the orbit increase with increasing values of λ.Next, we assume that the arrival process is exponentially distributed with parameter
. Fig (1.3), Fig (1.4), Fig (1.5) and Fig (1.6) show how the server’s busy period and vacation period probabilities, the expected number of customers in the system and the expected number of customers in the orbit increase with increasing values of λ.Next, we assume that the arrival process is exponentially distributed with parameter 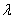 =0.1, the service time distribution function is exponential with mean
=0.1, the service time distribution function is exponential with mean  varying from 0.3 to 0.9, the retrial times follow an exponential distribution with LST
varying from 0.3 to 0.9, the retrial times follow an exponential distribution with LST with parameter
with parameter 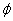 =0.8.The vacation time is also exponentially distributed with a mean = 0.25.Example 2:In this example, we study the effect of varying the service rate
=0.8.The vacation time is also exponentially distributed with a mean = 0.25.Example 2:In this example, we study the effect of varying the service rate 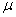 .From the Table-2, we observe that if the value of
.From the Table-2, we observe that if the value of 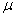 increases, the probabilities of idle time-
increases, the probabilities of idle time-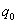 and
and 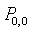 are decrease and the probabilities of busy time, expected no. of customers in the system and the ,expected no. of customers in the orbit increase.Fig(2.1) shows how
are decrease and the probabilities of busy time, expected no. of customers in the system and the ,expected no. of customers in the orbit increase.Fig(2.1) shows how 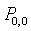 (i.e.) the probability of no customers in the system and the server is idle decreases with increasing values of
(i.e.) the probability of no customers in the system and the server is idle decreases with increasing values of 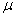 . Similarly, Fig(2.2) shows how the idle time probability of the server decreases with increasing values of
. Similarly, Fig(2.2) shows how the idle time probability of the server decreases with increasing values of 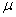 . Fig (2.3), Fig (2.4), Fig (2.5) shows how the server’s busy period probability, vacation time probability and the expected number of customers in the orbit increases with increasing values of
. Fig (2.3), Fig (2.4), Fig (2.5) shows how the server’s busy period probability, vacation time probability and the expected number of customers in the orbit increases with increasing values of 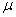 . Fig (2.6) shows how the expected numbers of customers in the system increases.
. Fig (2.6) shows how the expected numbers of customers in the system increases.
|
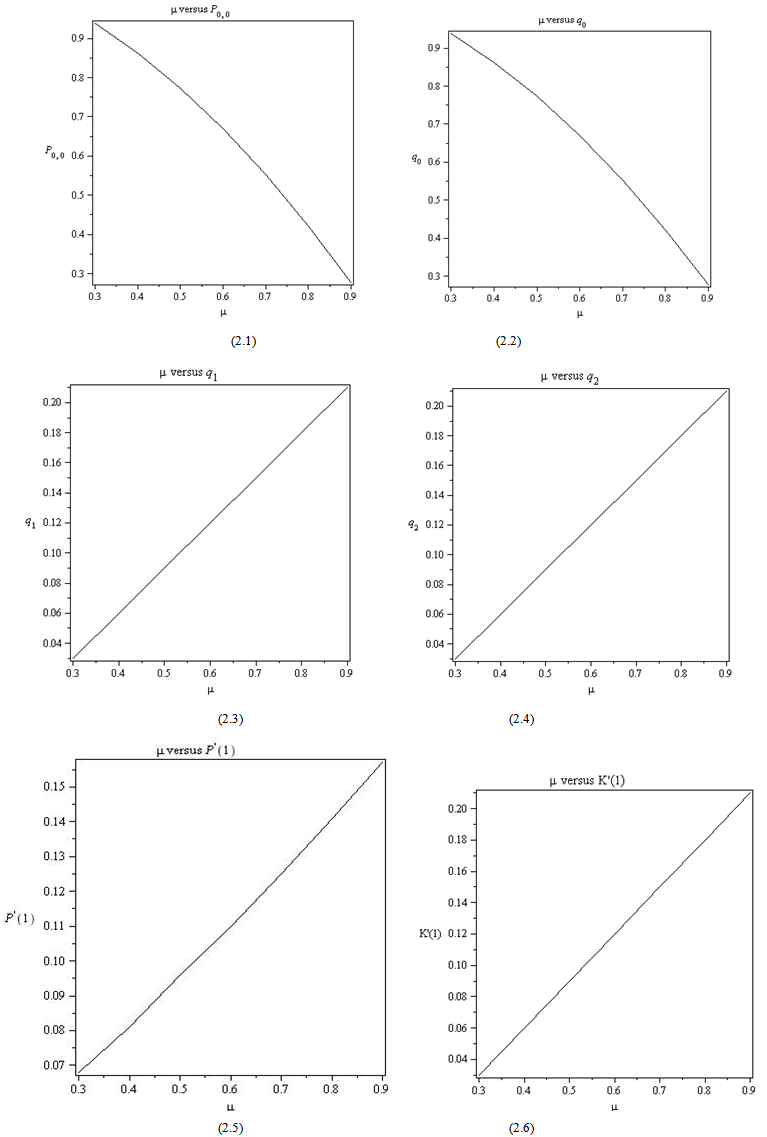 | Figure 2. Effect of varying  on various performance measures on various performance measures |
8. Conclusions
- In this paper, we have studied an M/G/1 retrial queue with general retrial times and a constant retrial policy with server vacations under a limited vacation discipline and a single vacation scheme. Existing results in the literature on retrial queues with vacations are concerned either with the exhaustive discipline or the gated discipline. Our aim is to increase the scope for then by considering a limited vacation discipline, where the server takes a vacation after completion of k (≥1) services.
ACKNOWLEDGEMENTS
- The authors are very grateful to the anonymous reviewers for their valuable suggestions to improve the paper in the present form.
Appendix
- We first present the derivation of the equations (1) to (8).Equation (1):
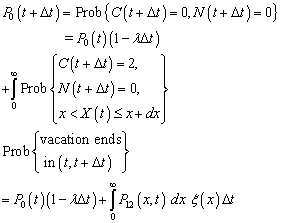 Dividing through out by Δt and taking limits as Δt→0, we get equation (1).Equation (2):
Dividing through out by Δt and taking limits as Δt→0, we get equation (1).Equation (2):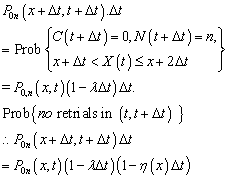 Dividing through out by (Δt)2 and taking limits as Δt→0, we obtain equation (2).Equations (3) to (8) are obtained by using similar arguments to those given above.Proof of theorem 4.1:From the above equations (11) & (12)
Dividing through out by (Δt)2 and taking limits as Δt→0, we obtain equation (2).Equations (3) to (8) are obtained by using similar arguments to those given above.Proof of theorem 4.1:From the above equations (11) & (12)  Proof of Theorem 5.1:In order to prove the sufficiency of the condition, we use the test function f(s) =s. The mean drift is then defined as
Proof of Theorem 5.1:In order to prove the sufficiency of the condition, we use the test function f(s) =s. The mean drift is then defined as 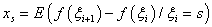 For
For 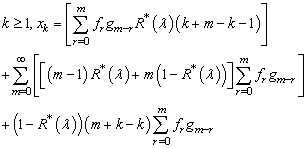 Where
Where 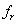 = Probability of r arrivals during the vacation time.
= Probability of r arrivals during the vacation time.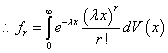
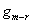 = probability of m-r arrivals during the service of a customer.
= probability of m-r arrivals during the service of a customer.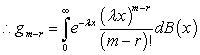
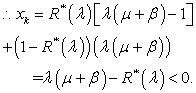 If
If 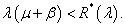 Foster’s criterion, the embedded Markov chain and hence our process is stable if
Foster’s criterion, the embedded Markov chain and hence our process is stable if 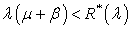 .The condition
.The condition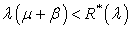 is also a necessary condition. This can be observed from equation (38), since, otherwise
is also a necessary condition. This can be observed from equation (38), since, otherwise 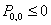 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML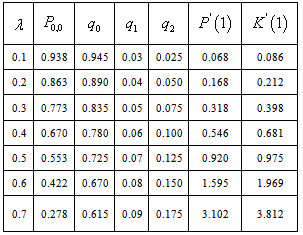
 on various performance measures
on various performance measures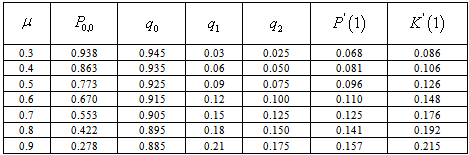
 /G/1retrial queue with Bernoulli schedules and general retrial times. Asia-Pacific Journal of Operational Research, 19,177-194, (2002).
/G/1retrial queue with Bernoulli schedules and general retrial times. Asia-Pacific Journal of Operational Research, 19,177-194, (2002).