1. Introduction

The jet withno pressure imbalanceis called free turbulent jet which hasa large axial velocity gradient present within a thin region in the radial direction. In other words, high velocity fluid is surrounded by a stationary fluid, causing the formation of mixing layer at their interface, also called the shear layer, where transition to turbulence occurs. In the turbulent jets, gradients of mean velocity, turbulence intensities and turbulent stresses are negligible in the axial direction compared to the radial direction. Flow inside the jet is highly turbulent in nature, where a strong mixing takes place due to the presence of eddies of multiple length scales. The turbulent eddies penetrate into the stationary fluid surrounding the jet due to intermittency and ambient fluid is entrained into the turbulent region. Due to the entrainment of the surrounding fluid and strong mixing within the jet, the shear layer (mixing layer) widens rapidly in the streamwise direction and velocity gradients in the radial direction decrease in the streamwise direction. The enlargement of the jet in the streamwise direction affects decrease of time averaged velocity of the jet at its centerline.

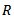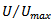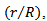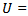The turbulence in the jet is self-similar, where the length scale is radius of the jet at any section and velocity scale is the maximum time averaged velocity taken at the jet centerline. i.e., is a function of where time averaged streamwise velocity at any radial distance 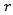from the jet centerline, 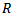is radius of the jet at that section. Similarly, Reynolds stresses are also functions of 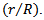These functions are independent of distance from the jet origin, therefore turbulent jets are called as self-preserving turbulent free jets. Another important feature of the free turbulent jets is the occurrence of the maximum Reynolds stresses where time averaged mean velocity gradient is maximum. But, all these characteristic are typically exhibited by a subsonic jet only, which is always correctly-expanded.

But, it is well known that unlike subsonic jets, the sonic jets may be either correctly-expanded and/ or underexpanded, which is highly turbulent in nature. It is due to the fact that in the previous case there does not exists any pressure imbalance but in later case pressure imbalance may play its role depending upon then nozzle operating pressure ratio. The pressure imbalance at the nozzle exit, generate a complex shock-cell structure in the jet core region. The underexpanded state leads to the formation of expansion waves at the jet exit which extend to the free jet boundary, and get reflected as weak compression waves. These compression waves coalesce to form the intercepting shocks in the interior of the jet and thus, the core of the underexpanded jet is dominated by periodic shock-cell structures. Further, it is also established that for an efficient mixing of a free jet with the environment fluid, the mass entraining large scale vortices and mixing promoting small scale vortices should be in optimum proportion. However, identifying this optimum promotion is physically impossible, but this difficulty can be overcome by manipulating the size of the mixing promoting vortices [1]. From the vortex theory, it can be seen that the asymmetric jets shed the vortices of mixed size in comparison to their circular counterpart. In circular jets, the curvature is same across the jet boundary; therefore, the mixing is not rapid. On the other hand, in asymmetricjets due to their continuous variation in radius of curvature of the nozzle exit, shed the vortices of continuously varying size. These mixed size vortices promote both large-scale mass entrainment and small-scale mixing. The circular jets can be made asymmetric by controlling them. The control of jets can be broadly classified into two categories, the first one is the active control requiring an auxiliary power source whereas, the other passive control strategies are based upon geometrical modifications of the nozzle exit, which alter the flow development downstream of the nozzle relative to a conventional circular nozzle. In the past, many studies have been carried out on passive controlled jets such as, notches, grooves, tabs, cross-wire, etc., which makes the jet non-circular [2-10]. Several researchers have focused their studies on underexpanded jets to understand the complex shock cell structures. The shape of these shock structure becomes highly asymmetric when the jet exits from the non-circular orifice/nozzle exit geometries [11-14]. As a result of this, flow structures of different sizes form at the jet boundary and the jet spreads differently along different planes. This differential spread rate, the major and minor axes of elliptic jet switch after a certain distance downstream of the nozzle exit. The axis-switching phenomenon has been reported by many researchers in the past. Hussain and Husain, (1989) [15], observed that the location and number of axis-switching were strongly dependent on the initial conditions of the jet. Quinn, (1989) [16], observed two axis-switches of the major and minor axes and found that the jet attains an axi-symmetric shape at about 30 equivalent slot diameters downstream of the exit plane. Ho and Gutmark, (1987) [17], even reported three axis-switching in elliptic jets. The asymmetric jets are also drawnby nozzles with non-circular cross-section such as elliptic, rectangular, triangular, etc. The studies on non-circular jets show that the jet produces fine scale mixing at the corners or high curvature regions and is good suction creators at the low curvature/flat side regions resulting in high entrainment. Elliptic jets with smooth and continuous variation in radius of curvature fall between circular and highly non-circular (such as, rectangular, triangular) jets. Due to this smooth and continuous variation in radius of curvature, vortices generated at the exit will be of continuously varying size. These mixed size vortices promote both large and small-scale mixing. Whereas in circular jets, the curvature is same across the jet boundary, therefore the mixing is not as rapid as in elliptic jets. Gutmark et al(1991) [18], studied an elliptic jet of aspect ratio 3:1 and found enhanced mixing characteristics of the elliptic supersonic jet compared to a circular supersonic jet at underexpanded conditions. Passive control of fuel-air mixing using asymmetric jet exit geometry is an attractive pollution abatement technique [19]. For instance, the injection of longitudinal and azimuthal vortices in the shear layers from an elliptic co-flow can control the mixing of fuel and air, because these vortices are formed in the elliptic jet as a result of asymmetric self-induction of the vortex ring structures. The asymmetry causes instability in the flow field at the jet exit. Hence, an asymmetric jet tends to remove its instability by becoming symmetric downstream. This occurs as the major axis becomes small and the minor axis becomes large in order to become symmetric leading to axis-switching. Gollahalli et al (2002) [19], studied the effects of elliptic co-flow on the structure of a propane jet flame. The results were compared with the measurements from the experiments on the same burner in a circular co-flow. They found that, the elliptic co-flow flame produced less soot than the circular co-flow flame. Gutmark et al (1989) [20], found that, the elliptic jets burn 10% more efficiently than circular jets as a consequence of better mixing of fuel and air. Yoon and Lee (2003) [21], investigated the near field structure of an elliptic jet using stereoscopic particle image velocimetry and reported that the total entrainment rate of the elliptic jet was larger than that of the circular jet. Quinn (2007) [22], showed that mixing in an elliptic jet issuing from a sharp-edged orifice plate is higher than in elliptic jets issuing from contoured elliptic nozzles and in round jets. Chauhan et al (2015) [23], have compared the centerline pressure decay of 2:1elliptic sonic jet issuing from an orifice and a convergent nozzle under favorable pressure gradients. In this study they have varied the nozzle pressure ratios (NPR) from 2 to 5, in steps of one. They found that except at NPR 2 which is a correctly-expanded state, the decay is found to be faster for elliptic nozzle than elliptic orifice at all other NPRs. Though, the researchers have studied the mixing characteristics of elliptic jets at a length but they did not quantify the efficacy of elliptic jets over their circular counterpart. With this motivation, the present study aims at evaluating the efficacy of jet issuing from 2:1 elliptic nozzle has been investigated experimentally, in the presence of favorable pressure gradients. To quantify the mixing enhancement the Pitot pressure are measured along the jet centerline and the waves prevailing in the sonic jet coreareanalyzed using the shadowgraph optical flow visualization method.

2. Experimental Methodology

The brass made circular nozzle and sonic elliptical nozzle of aspect ratio 2:1, have been used for investigations. The equivalent diameter of the nozzle is found to be 10 mm. The schematic diagram of circular and elliptic nozzles is shown in Figure 1.

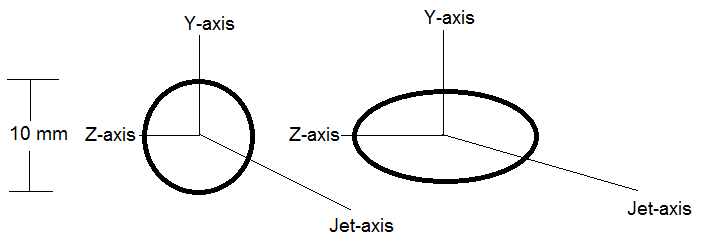Figure 1. Schematic diagram of circular and elliptic nozzles

The pressure measurement has been performed using Pitot or stagnation pressure probe, mounted on a 3-dimensional traverse mechanism with 6-degrees of freedom (capable of 3-translational and 3-rotational motions). The traverse mechanism has been provided with moving Vernier and stationary main scales having a translational least count of 0.1 mm and the rotational least count of 1°. The Pitot probe is connected to a 16-channel electronic pressure scanner (transducer), which averages 250 samples per second for each pressure reading. The manufacturer provided transducer accuracy is ±0.15%. This pressure scanner is integrated with data acquisition unit, consisting of a computer installed with Lab-View software. From the uncertainty analysis, precision of the pressure readings were found to be in between ±3%. For the qualitative analysis of the sonic jets, the second order density based shadowgraph flow visualization technique has been used.

3. Results and Discussion

It is understood that the sonic jet core consists of a large number of compression and expansion waves which are non-simple waves and change the Mach number of the flow passing through them. As a result, the Mach number at every local point assumes different values. Therefore, it is a usual practice to use the Pitot pressure distribution measured as it is in the non-dimensional form to characterize the jet field; such as the jet core length, shock-cell length, the acceleration zones, the characteristic decay and the fully developed zone. The Pitot pressure 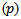distribution measured along the jet centerline (X-axis) has been non-dimensionalized with the settling chamber stagnation pressure 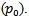The axial distance 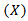has been made non-dimensional with the nozzle exit equivalent diameter

3.1. Centerline Pitot Pressure Decay

Soon after exiting the nozzle, due to shearing action between high momentum jet and almost stagnant surrounding fluid, the large scale eddies are generated at the jet boundary. These large scale vortices, which have shorter life span, are responsible in engulfing surrounding zero momentum fluid into the jet. In this mixing process, these vortices breakdown into large number smaller eddies, responsible for mixing promotion. The jet-centerline Pitot-pressure decay is a measure of jet mixing with the entrained fluid mass. The decay can clearly show the extent of sonic jet core, which is defined as the axial distance up to which the nozzle exit velocity remains unaffected for subsonic jets and the axial extent up to which pressure fluctuations prevails for sonic jets [1]. The non-dimensional jet-centerline pressure decay plots of the elliptic jet of aspect ratio 2:1 and the circular jet, at NPRs 2.5, 3.5 and 4.5 are given in Figures 2(a)-(c). Since, the sonic jet at NPR 2, is almost correctly-expanded (p_e/p_b = 1) and thus at NPR 2.5, the jet is in moderate underexpanded state at the nozzle exit (Figure 2(a)). This implies that the waves prevailing in the core are weak in nature. It is also seen that the jet core for both elliptic and circular jets extends upto 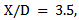therefore; there existsa small pressure imbalance at the nozzle exit. However, the waves present in the elliptic jet are weak in nature, which is a direct evidence of enhanced mixing owing to its capability in shedding vortices of mixed size. The jets become almost fully developed beyond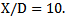

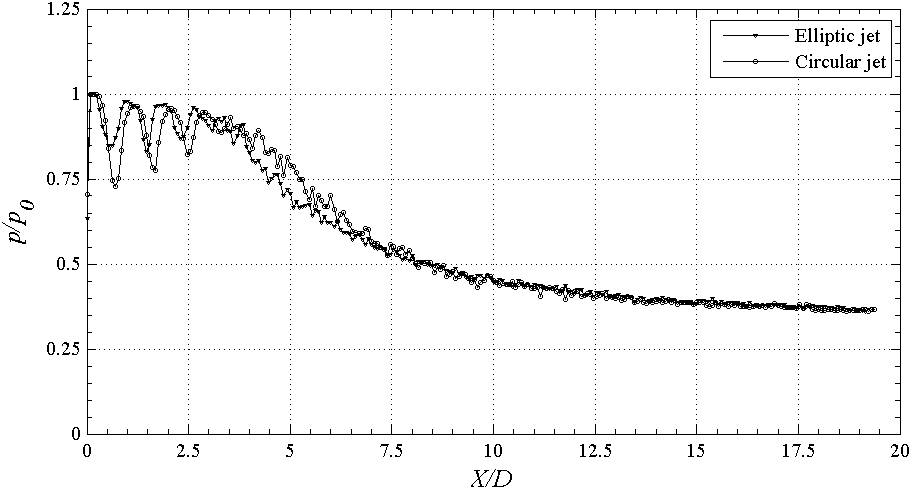Figure 2(a). Centerline pressure decay at NPR 2.5 (underexpanded)

When the NPR is increased to 3.5, for both elliptic as well as circular jets even though the core lengthsextend only upto 4D, but the shock-cells become longer and the waves become stronger as shown in Figure 2(b). The stronger underexpansion fans present at the nozzle exit accelerates the flow to higher Mach number downstream. The flow keeps accelerating to higher Mach numbers till the first cross-over point (first minima in Figure 2(b)) is reached. After this point, the flow becomes subsonic and it starts accelerating again to higher subsonic Mach number by exchanging momentum with the surrounding fluid. The acceleration continues till it encounters second cross-over point at the jet centerline, formed by meeting of expansion fans from every side and the cycle again repeats. Here also, the waves present in elliptic jet core become weak in nature as compared to the waves in circular jet core. At this NPR, the jets become almost fully developed around 9D.

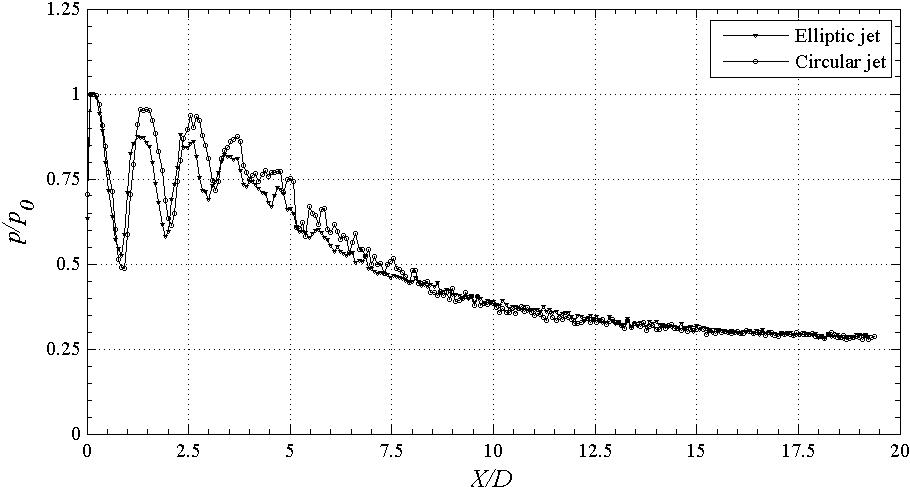Figure 2(b). Centerline pressure decay at NPR 3.5 (underexpanded)

At the highest tested underexpansion level corresponding to NPR 4.5, the stronger expansion fans are formed due to large pressure imbalance at the nozzle exit in both the cases as shown in Figure 2(c). The flow passing through these expansion fans are accelerated to considerably higher Mach numbers at which Mach-disk begins to form. The flow after passing through ‘Mach-disk’ has significantly lower Mach numbers and does not have enough momentum to get accelerated further. The ‘Mach-disk’ formation is very prominent in circular jet than the elliptic jet. This may be because of an early ‘axis-switch’ of jet cross-section soon after exiting and thus rapid mixing in case of elliptic jet. Hence, in this case the first shock-cell is very prominent than the rest of shock-cells due to ‘Mach-disk’ formation. Although, the core length decreases to 3.5Das compared to previous case, but the jet becomes almost fully developed only beyond 10D.

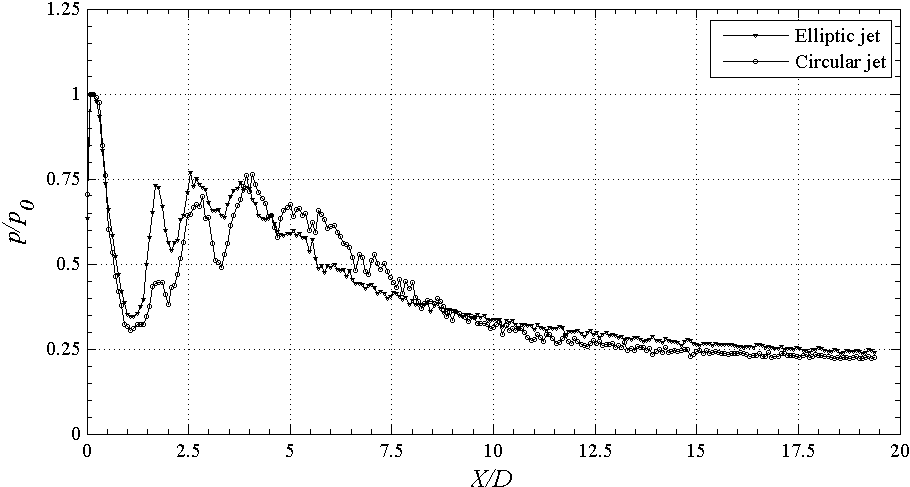Figure 2(c). Centerline pressure decay at NPR 4.5 (underexpanded)

The above results show that the reduction in jet core length is strongly governed by the levels of expansion at the nozzle exit. The elliptical nozzle generating varying size vortices from longer to smaller ones at the nozzle exit is found to be beneficial from mixing promotion point of view.

3.2. Shadowgraphic Flow Visualization

The waves prevailing in the elliptic and circular jets flow fields are visualized with shadowgraph technique. The images recorded with a still camera are presented in this section. For the elliptic jets, the images are taken in the directions along the major axis and normal to major axis of elliptic nozzle. The shadowgraph pictures of the flow field from NPR 2.5, 3.5 and 4.5, are shown in Figures 3(a)-(c). Since, all the investigated NPRs of the present study correspond to underexpanded state of the jet, the expansion fans form at the edge of the nozzles. These expansion waves extend to the jet periphery and get reflected as compression waves due to unlike reflection of waves. These compression waves coalesce to form the intercepting shock in the interior of the jet, and thus the core of the underexpanded jet is dominated by periodic shock cell structure.

Due to moderate underexpansion level at NPR 2.5, generates weak waves in the core of ellipticsonic jet as seen in Figure 3(a). These weak waves cause some light bright and dark regions in the jet core. The shorter core lengths and weaker shock-cell structure, as observed in the centerline pressure decay plots can beseen in the shadowgraph pictures as well. From these images, it can also be seen that the shock-cell structures diverge along the major axis plane and converge along the minor axis plane (Figures 3(a)). The differential spread rate in these two directions generates shear and leads to the faster decay of jet.

Figure 3(a). Shadowgraph images of sonic jet at NPR 2.5

However, when the underexpansion level is increased to 3.5, the periodic shock-cell structure begins to appear in the core of jet (Figure 3(b)). This being a comparatively higher underexpanded state of jets, there would be a strong expansion fan, due to higher underexpansion level prevailing at the nozzle exit, form at the nozzle edges. This shock structure gradually gets diffused in the downstream direction by the mixing arising from the shear layer spreading towards the jet centerline and the surroundings. The shock passes through each other exhibit a tendency to form a “Mach-disk”. The shocks crossing-over each other get reflected from the inner boundaries of the jet as expansion waves and the process continues. Three prominent shock-cells are explicitly seen in the jet core. Further, with the increase of NPR, the lengths of first three to four shock cells, identifiable in these images, also increase.

Figure 3(b). Shadowgraph images of sonic jet at NPR 3.5

At the highest tested NPR of 4.5 also, the strong expansion fans at the nozzle exit leads to ‘Mach-disk’ formation in the first cell (Figure 3(c)). The waves of higher strength show typical characteristics of sonic jets at higher underexpansion level.

Figure 3(c). Shadowgraph images of sonic jet at NPR 4.5

From the flow visualization images of elliptic jet, it is clearly seen that the different jet spread rates in two different planes leads to ‘axis-switch’, responsible for mixing enhancement. The elliptic jet is able to shed the vortices of mixed size right from the nozzle exit and hence promotes an early ‘axis-switch’ compared to its circular counterpart. The above results support the findings as obtained in centerline pressure decay section.

4. Conclusions

In the present study, the jet propagation, issuing from circular and elliptic sonic jets operated under varied levels of underexpansion, is experimentally investigated. It was found that the reduction in sonic jet core length is strongly governed by the levels of expansion at the nozzle exit. However, the elliptical nozzle capable of shedding vortices of mixed size was found to be effective in superior mixing. The shadowgraph images confirmed the efficacy of elliptic jet compared to circular jet in mixing augmentation and weakening the shock-cell structures, which is advantageous from acoustics point of view.

ACKNOWLEDGEMENTS

The authors acknowledge the financial support provided by Sponsored Research and Industrial Consultancy (SRIC), Indian Institute of Technology Kharagpur in order to complete the present investigation. The authors also acknowledge the High Speed Aerodynamics Laboratory at Indian Institute of Technology Kanpur, where the experiments in the present study have been conducted.

Nomenclature

AR = Aspectratio (ratio of semi-major axis to semi-minor axis lengths)

D = Equivalentdiameter

NPR = Nozzle Pressure Ratio, p/p₀

p_a = Atmospheric pressure

p_e= Nozzle exit pressure

p₀ = Settling chamber pressure

p = Pitot pressure in the jet field

X = Coordinate along the jet axis