1. Introduction

The vast quanta of knowledge presently available and the continuous research currently being carried out stand testimony to the importance associated with the jet plumes. This is owing to their extensive nature of applicability, from household appliances to space technology. However, the jets must be controlled before they are used for specific purposes. For example, the high speed jets find their applications both in powder metallurgy and oil well fire fighting but they must be suitably controlled in terms of varying jet speed and mass flow rate. Atypical schematic diagram of an uncontrolled subsonic free jet with different flow zones is shown in Fig. 1. The jet control aims at modifying the flow development to suit to the specific needs. The jet control techniques can be broadly classified into two namely, the active and passive control. Passive control may be permanent or deployable, but have no moving parts during operation. In contrast, active controls use energized actuators to dynamically manipulate flow phenomena. For example, pulsed jets use piezoelectric actuators foractive mixing enhancement.

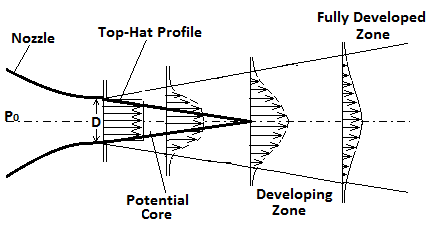Figure 1. Schematic diagram of different zones in the development of a subsonic jet

Although, many computational and experimental studies on jet controls are available in the literature, the present paper confines itself in reviewing only the numerical investigations carried out in the last around fifty years. Numerical simulation of jets becomes a cumbersome task because of the requirement for an appropriate turbulence model to accurately capture small and large scale entrainment, coherent structures, and the shock-cell structures in over-expanded and under-expanded nozzle exit conditions, as shown in schematic Figs. 2(a)-(b). In the following sections, we have made an attempt to highlight the CFD studies carried out in the evolution and control of the jets performed by various researchers from the very beginning to date.

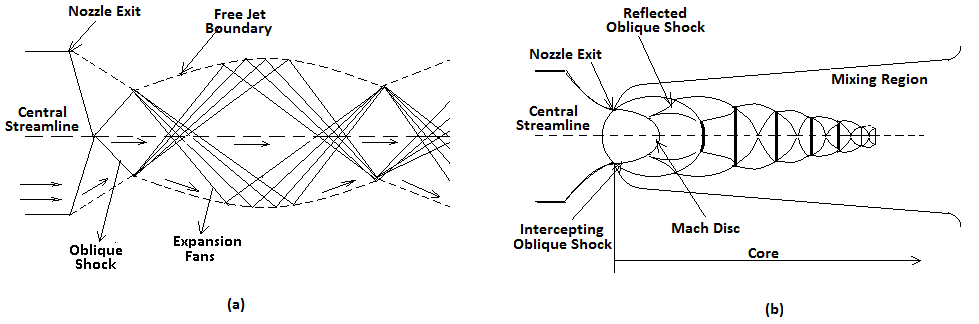Figure 2. Schematic diagrams of (a) overexpanded jet, (b) under expanded jet

1.1. Early Numerical Studies in Jet Flows

According to the literature, early theoretical and numerical studies are limited in number both due to the time dependent non-linear characteristics of the Navier-Stokes equations and unavailability of high performance computing facilities. In early sixties, Batchelorand Gill (1962) [1] mathematically analyzed the stability of steady axi-symmetric parallel flows of uniform fluid in the absence of rigid boundaries. For this case, a jet at sufficiently high Reynolds number for the angle of viscous spreading to be small was considered as a typical example of the primary flows. Since, jets are known to be unstable, presumably to infinitesimal disturbances, they considered the typical small disturbance as a Fourier component with sinusoidal dependence. With this base, they developed a time dependent solution using the classical linearized theory to analyse the stability characteristics in the limit of large Reynolds number. Beavers and Wilson (1970) [2], represented the inviscid flow domain by discrete arrays of point vortices. However, first realisticattempt to numerically compute and investigate the free jet chracterisctics in subsonic flow regime can be considered asstarted in 1974. Although in the subsonic flow, the absence of waves might make the computations easier, understading the vortex dynamics precisely and accurate capturing of turbulent structures poses real challenges. Grant (1974) [3], used the time-independent Navier-Stokes equation to study the instabilities associated with the low subsonic axi-symmetric jets. From theisodines and the stream function profiles at various Reynolds numbers, it was found that the jet field is dominated by the large-scale vortical-structures. Due to initial perturbations, the wavelength of vortex shedding in the jet field was found to be slightly varying. However, the results obtained from the numerical model were found to be in reasonably good agreement with the experiments. Matsuda, et.al (1987) [4], analyzed the under-expanded supersonic jet evolution numerically. They adopted the time-averaged second order Osher upwind scheme to solve the Euler equations for a compressible ideal gas at various boundary conditions. Numerical results were found to be sensitive to the suitability of the conditions imposed. By the density contours plots, it was shown that the initially stable wave that dominated jet sturucture can be destabilized by the formation of Kelvin-Helmholtz vortex rings. The numerical results were compared with the experimentally obtained Schlieren photographs. The researchers observed a turbulent flow with vortices and shocks in the former, and a complete shock-cell structure in the latter. From this study, it was strongly suggested that a time-independent or a time-converged solution cannot be expected without making a suitable time-averaging of the time-dependent solution.

Agui and Hesselink (1988) [5] analyzed the instabilities of an acoustically excited subsonic co-flowing jet both experimentally and computationally usingvortex-element method. With the assumption that the jet divergence does not play a vital role in the evolution and development of streamwise vortices, they modelled a periodically excited jet. By using the vortex-element method, the vorticity distribution and the mass entrainment on the basis of surface-to-volume ratio were computed. The numerical results were compared with results obtained through experiemnts and it was seen that the morphology of the flow possesses vortices, mainly concentrated into a single large-scale vortex ring. Instead of vortex-element method, Martin and Meiburg (1991) [6] used vortex filament method to simulate the subsonic jet vortex dynamics. They assumed the flow to be inviscid and explained the mechanisms governing the jet evolution by spatially periodic calculations. The study was intended to the understanding of processes leading to the concentration, reorientation and stretching of the vorticity in the uncontrolled jet and for the jet induced due to sinusoidal perturbations in the azimuthal direction. They found that the evolution of the vortex rings depends on the ratio of thejet radius to its shear layer momentum thickness Furthermore, they also observed that the rate at which streamwise vorticity develops is strongly affected by the ratio of the streamwise and azimuthal perturbation amplitudes. However, the assumption of inviscid flow in the vortex filament technique is obviously unable to capture the viscous effects in the actual flow field. Miller et al (1995) [7] studied the entrainment of the subsonic jet flows originating from elliptic, rectangular and triangular nozzles with aspect ratios of 1:1 and 2:1 using the compressible Navier-Stokes equations, and a passive scalar conservation equation with the Fourier heat conduction and the Fickian diffusion assumptions. These equations were solved numerically without resorting to any turbulence or imposed subgrid models. The results were compared with those of a circular jet of the same equivalent diameter to determine the relative efficiency of non-circular nozzles in mixing enhancement. Though the flow structure was predicted, but the effectiveness of the compressible or the time-independent Navier-Stokes equation in the simulation of subsonic jet or in predicting the three-dimensional vortical structures, remained unexplained. There remains a necessity to obtain the accurate aerodynamic and aeroacoustic prediction tools for analyzing exhaust nozzle systems and the turbulent jet flowfields. To this end, initial successful attempts were made using the Reynolds-Averaged Navier-Stokes (RANS) method. A brief summary of some of the remarkable attempts in this direction is given below.

1.2. Application of Reynolds-Averaged Navier-Stokes (RANS) Method in Jet Flows

The robustness of the numerical scheme is very important to simulate the supersonic free jet as strong discontinuities present in the flow field have a tendency to destabilize the flow. Researchers have investigated the effectiveness of various computational methods in simulating the shear driven supersonic jetflows. The application of a reliable technique in computing the supersonic jet flow field characteristics originated in 1996. To this end, the Reynolds-Averaged Navier–Stokes (RANS) methodis the most conventional approach to calculate the shear flows. The RANS method consists of time-averaged equations of motion for fluid flow. Reynolds (1895) [8] proposed the method of Reynolds decomposition, where an instantaneous quantity, for example ‘u’ is decomposed into 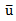and u' i.e., intoits time-averaged and fluctuating quantities respectively. The RANS equations are primarily used in analyzing turbulent flows, with approximations based on knowledge of the flow properties to give approximate time-averaged solutions to the Navier–Stokes equations. This method attempts to model all turbulent fluid dynamic effects with a turbulence model. Currently, RANS methods are used for a vast majority of calculations. Two-equation models, such as k-ϵ, Menter’s SST formulations and k-ω modelare widely used to solve for the turbulent kinetic energy in the jet environment.

Thies and Tam (1996) [9] used the k-ϵmodel with a correction factor as developed by Pope (1978) [10], and Sarkarand Lakshmanan (1991) [11]. They attempted to predict the flow characteristics of the jets having high convective Mach number. The axisymmetric and non-axisymmetric jet mean flow results over the Mach number range of 0.4-2.0 were compared with the available experimental data. Interestingly, although this model was observed to reproduce the core length and shock-cell length to some extent, the quantitative data such as turbulent intensities were found to be in error. It has now been known that the standard k-ϵ model always over predicts the turbulent kinetic energy growth rate in compressible mixing layer types of flows such as a free high-speed jet. Although, the characteristics and dynamics of fine-scale turbulence may be the same for all turbulent flows, the large turbulence structures, having dimensions comparable to the local length scale of the flow, are significantly influenced by local boundary conditions and geometry. Thus, Thiesand Tam (1996) [9] proposed that there is no universally applicable turbulence model and model has to be chosen depending upon the flow configuration. This creates the necessity to introduce limiting and correction terms. Durbin (1996) [12] proposed to limit the eigenvalues of the Reynolds stress. He mentioned that the limits of the Reynolds stress eigen values must be between zero and twice of the turbulent kinetic energy. The ‘Durbin realizable model’ is proposed to be effective up to Mach 3.

Further examination of the effect of compressibility on turbulent flows led to the conclusion that the compressibility effects can be categorized into two basic groups namely, the dilatational and structural compressibility effects. The dilatational compressibility effects are related to variations of the mean mass desnity or variations in the instantaneous mass density whereas, the structural compressibility has significant influence on the structure of turbulent flows. Zeman (1990) [13] and Sarkaret al (1991) [14] modeled the dilatation dissipation based on the results of direct numerical simulation of isotropic compressible turbulence subjected to strong compression. Heinz (2003) [15] proposed a model to account for the structural compressibility effects by re-modeling the turbulence production term. These compressibility corrections terms are employed in the standard k-ϵ turbulencemodel. Several modified linear two-equation turbulence models developed specifically to improve jet flow predictions were compared to the standard RANS turbulence models. Tandraet. al (2006) [16] developed a modified model of k-epsilon with three additional terms to predict the flow properties of high subsonic and supersonic jets up to Mach 2.8. Combining the correction terms proposed by Durbin (1996) [12], Sarkar et al (1991) [14], and Heinz (2003) [15], the modified k-ϵ model was formulated. The performance of the developed numerical model in predicting the free jet flows, a jet propagating between smooth flat plates and a jet impact on an object was tested. The jet centerline velocity, centerline pressure, radial velocity and pressure profiles of the free jet of Mach 0.67, 2.22, 2.3 and 2.8 were compared with the available experimental data. A good agreement with the data was obtained, demonstrating the efficacy of the modeified k-ϵ model. Berget al (2006) [17] compared the two equation turbulence models of k-ω and standard k-ϵ incalculating the properties of a turbulent flow from a aspect ratio 2.0 rectangular Mach 0.17 free jet. Two types of inlet velocity profile boundary conditions such as uniform profile and profile from experimental results were analyzed by two turbulence models of k–ε and k–ω. The results concluded that, the simulation by k–ε model with parameters adapted from experimental results best predicted the centerline velocity decay of the jet. It was found that the conventional density based algorithms become inefficient and often unstable at low Mach numbers.

Birky and Page (2001) [18] suggested the adaption of modified pressure based methodology with compressibility correction in simulating the sonic jet in under expanded condition. They proposed that the pressure-based approach with a correctly formulated compressible treatment can accurately compute flows containing both high and low Mach number zones. This numerical scheme uses a basic first-order upwind scheme discretized in an implicit manner. They adapted a higher-order discretization scheme using a total variation diminishing (TVD) method as an explicit correction to the basic upwind scheme. The flow of interest contains a high-speed jet core exhausting into ambient where the flow is at rest. For nozzle pressure ratio (NPR) 3.5, the results from the standard k-ϵ with and without compressibility correction are compared with their experimental counterpart. By varying the NPR from 3.5 to 30, the location of the Mach disk was found to be in agreement with the experimental data. It was observed that the k-ϵ model with compressibility correction produces a faster decay as compared to the experimental results even though the shock cell lengths were in good agreement. The compressibility correction to the turbulence model was found to have almost no effect on the shock cell structure. Chauvetet al, (2007) [19] used the Spalart-Allmaras turbulence model in predicting the jet flow characteristics. From the series of RANS computation and experiments conducted, they showed that the under expanded sonic jets experienced higher mixing enhancement under the influence of radially injected secondary jets. The Spalart-Allmaras model was used to correlate the strong distortion of the jet interface under the action of the longitudinal vortices. Various nozzle configuations having 2, 4 and 8 numbers of radial injections and various secondary orifice jet aspect ratios of 0.5, 1.0, 2.5 and 10 were studied and numerical results were compared with the obtained experimental data. They proposed that, the ideal configuration for an efficient mixing should have four or less number of injectors with a low aspect ratio orifice to prevent premature vortex interaction and excessive diffusion. They stated that the modification of the inside supersonic waves do not contribute to the mixing enhancement. The comparison of plots depicting the numerical and experimental results exibited some discrepencies, which neccesitated the adoption of improved numerical schemes, as discussed in the following sections.

1.3. Jet Flow Modeling by Large Eddy Simulation (LES)

From the above, it is clear that the important details of the jet flow features such as core length, jet spreading rate, mixing and turbulent characteristics could not be predicted with the desired accuracy by any of the RANS models. These turbulence models were found to suffer from limitations for jets with significant three-dimensionality, compressibility and high temperature streams. Further, RANS methods can only provide time-averaged turbulent information. However, inspite of these limitations, RANS methods can frequently capture the trends exhibited by experiments when altering the geometry or flow conditions. This fact coupled with the advantage that RANS solutions are relatively inexpensive means that these methods still have a place for designing nozzle systems. Further improvements in RANS methods for the prediction of jet flows will be incremental at best. Hence the next logical choice is to adopt the unsteady methods of Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS), for large advances in accuracy and fidelity. Owing to the crucial role of turbulence dynamics and complex geometries, Large Eddy Simulation (LES) tool has growing importance in the field of jet simulation at present. A survey of LES research as applied to turbulent jet flows is documented.

Hilgers (2000) [20], carried out the LES of a jet and found that the Strouhal number grows with amplitude of the major actuation parameter that enhances mixing and jet spreading. SthandSta, which correspond to the preferred Strouhal number of the jet and twice its value respectively, were found for all the Reynolds number investigated (Re = 1500, Re = 6000 and Re = 100,000). The Strouhalnumber showed that the spreading of the jet was larger at higher Reynolds number. No comparisons with the experimental data or with other numerical scheme was done by the researcher to validate the accuracy of the results obtained. Terrier and Lu (2001) [21] used the LES scheme in silmulating the jet, which is controlled by a step incorporated right after the throat of the nozzle. They performed both experimental and computational investigation to show that the control device provided good thrust recovery in comparison to the nozzle without the step under overexpansion of the jet at the nozzle exit. The computational simulation was performed with FALCON for a full-scale nozzle using a finite volume approach on a multiple block structured grid to achieve greater conservation qualities than comparable finite difference codes. The over-expanded nozzle produced a complex shock-boundary layer interactions toward the nozzle exit, but it was reported that when a step was added near the downstream of the nozzle throat it reduced the overexpansion, thereby yielding a better pressure recovery in the divergent region. The computed value of Cfg (thrust coefficient), showed a 2.5% improvement in the performance in comparison to the plain nozzle. These CFD results were verified by the sub-scale model testing. In the cases of excited and forced jets, the LES scheme was tested for accuracy and stability. Maidi and Lesieur (2005) [22] used LES filtered structure functional model to simulate the high Reynolds number (Re ≈ 36000) turbulent flows for Mach 0.7 and 1.4 jets. They used abasic velocity profile close to a top-hat, combined with small inlet perturbations. At Mach 0.7, from the LES turbulent flow visualization results, they observed the shedding of quasi-axisymmetric vortex rings with longitudinal hairpin like vortices from the jets. However, these were reported to be disappeared in Mach 1.4 flow, and instead primary vortices undergoing alternate pairing form was observed, which lead to an increase of 27% in jet core length. They concluded from the LES analysis of Reynolds stresses that the turbulence intensities decreased with increasing Mach number, however, with only a very weak effect on the stream wise normal stress. Maidi, et al (2006) [23], extended their work on LES to study the effect of different types of upstream forcing on Mach 0.7 and Mach 1.4 round jets. They conducted tests at four different excitation frequencies and found the optimum frequency at which the jet spreading was maximum. They reported the highest jet spreading rate at Mach 0.7, with the varicose–flapping excitation, with a core length reduction of 27% as compared to unexcited jets. At Mach 1.4 jet case, the most efficient strategy for jet control was obtained by using a flapping excitation at the second sub-harmonic frequency with a core length reduction of 28%. This was interpreted to cause a quick transition to turbulence and lead to the more enhanced mixing rate of the jet.

The application of LES for the prediction of jet characteristics of an actuator controlled device was carried out by Faivre and Poinsot (2013) [24]. They developed an actuator device made up of four small jets feeding the primary jet flow and these are oriented to add an azimuthal component to the velocity field. Experimental study of three different configuration of the jet (α=90°, 45° at 30mm and α=90° at 8mm from the nozzle exit) was quantified by Schlieren photographs, PLIF and hot wire anemometry results. It was found the most efficient configuration in terms of mixing and jet spreading enhancement device, where actuation jets are located close to the nozzle and oriented to provide maximum swirl injection (α=90° at 8mm from the nozzle exit). The LES of both forced and unforced cases of actuator located at α=90° were also performed for better understanding of the production of vortices and mixing phenomenon at this configuration and instantaneous vorticity visualization has revealed the presence of secondary vortices due to actuator. However, the physics behind the production of secondary vortices was far from understanding in this study. The modified LES variants are formulated to eliminate the minor discrepancies in the flow field. Wang and McGuirk (2013) [25] carried out LES of a supersonicjet issued through a convergent-divergent nozzle of a high aspect ratio rectangular cross-section. They have adopted rescaling/recycling method (R2M) of LES in the generation of inlet conditions. Two different models of the Piomelli and Guerts Sub-grid scale (PGSGS) model and the Smagorinsky Sub-grid scale model (SSGS) were developed and compared with the available data from the RANS model. At the overexpanded nozzle pressure ratio of 2.5, the instantaneous turbulent eddy structures and the instantaneous axial velocity of the jet plumes were visualized for both the models. They observed that the eddy structures from the PGSGS model were more complex than those seen in the SSGS model simulation. Also appearance of the Kelvin–Helmholtzlike structures in the SSGS simulation was interpreted as a failure of the model to capture the correct behavior of the boundary layer within the nozzle. The velocity profiles at the major and minor axes at various axial locations were plotted for both the PGSGS and SSGS models. They found that the Piomelli and Guerts Sub-grid scale model, with adopted rescaling/recycling method, was in good agreement with the available experimental data in better prediction of the shear layer growth. This leads to improved capture of shock cell behavior and core length of the plume. Suto et al. (2004) [26] tested two kinds of SGS model, one being the Smagorinsky Model (SM) and a Dynamic Smagorinsky Model (DSM) in the LES of turbulent round jets under four different Reynolds numbers ranging from 1200 to 106. The parameters of the DSM model were calculated using different levels of space filtering, which is unlike the SM model where the parameters are empirically deduced constants. They found that the quantitative accuracy of the DSM model was better than the SM model, while the SM model over predicts the mean velocity of the jet. The model coefficient was found to be large in the developed stage of the jet where as it was found to be small in the initial stage. Hence, they recommemded the optimization of the model coefficient in the DSM model for successful prediction of streamwise variation of the jet.

To gain insight of the flow characteristics, most LES simulations of jets have focused mainly on benchmark experiments of round nozzles. Thus modified nozzzle geometries for jet controls and for noise suppression, may not give the expected results when applied in the calculation without including the nozzle geometry itself. Thus the LES method was found to be effective only for simplest turbulence models in jet flow simulation and the specification of jet inflow conditions were also complicated. Additional effort is required to adapt current LES methods to handle such complex geometries. The computational time and cost of LES also increases exponentially as compared to RANS turbulence schemes, which makes LES one of the laborious schemes. A promising numerical scheme is the hybrid RANS/LES simulation where the upstream nozzle wall boundary layers are calculated using RANS and the jet regions are modeled using LES. The researchers intended to combine the advantages of both LES and RANS in affordable computational costs. This paved the way to hybrid RANS-LES schemes. Georgiadis and Bonis (2007) [27] proposed an alternative method for RANS in numerically simulation of the turbulent jet flow fields issuing from aircraft engine exhaust nozzles. The turbulence models of RANS were reported with limitations for jets with significant three-dimensionality, compressibility and high temperature streams. Thus, the researchers proposed a new approach of hybrid RANS/LES methods, where RANS was used to model the small-scale turbulence in wall boundary layers and LES was adapted in large-scale mixing regions. In this method, the LES is coupled with an explicit sub-grid scale (SGS) turbulence model. However, a more efficient hybrid RANS/ILES (LES with an implicit SGS model of turbulence), approach to effectively simulate the subsonic and supersonic jets from realistic nozzles, is suggested by Lyubimov (2008) [28]. The flow inside the nozzle was calculated using unsteady RANS approach with relatively coarse grids. ILES approach is realized in the jet region, where a fine grid was employed. The fifth-order monotonic scheme with additionally reduced scheme viscosity for approximating the convection terms in the Navier–Stokes equations ensures the accuracy of this method. Calculations were performed for jets from different nozzle configurations such as conical, chevron, and coaxial jets. The effect of the Mach number and the jet temperature at the exit of nozzle on the fluctuations of longitudinal component of velocity in the mixing layer was investigated for conical nozzles. The level of turbulence intensity is predicted both on the jet-axis and in the shear layers. The turbulence intensity values calculated with the computational grids of 5.0 X 105–1.2 X 106 nodes were found in accordance with the experimental data. Further improvements need to be incorporated to develop the proper interfaces between the RANS and LES regions.

LES methods require high-order numerical schemes, which do not lend themselves well to complicated grid topologies. Furthermore, the treatment of boundary conditions is one of the most critical issues in computational fluid dynamics. This is because of compressible solver’s accuracy, which is strongly sensitive to boundary condition, and may be spoiled by spurious numerical reflections generated at open boundaries. A general methodology in organizing the incoming and outgoing waves based on the Navier-Stokes Characteristic Boundary Conditions (NSCBC), was first suggested by Poinsot and Lele (1992) [29]. Lodato, et. al (2008) [30] extended the 3-dimensional NSCBC to account for convection and pressure gradients in boundary planes. The system is augmented with an additional transport equation for a passive scalar Z (diffusing according to the Fick’s law), which carries informations on turbulent scalar mixing. They proposed a systematic strategy for dealing the edges and corners and developed compatibility conditions for inlet/outlet and wall/outlet boundaries. Both, Direct Numerical Simulation (DNS) and Large Eddy Simulation (LES) studies were performed. It was seen that, 3-dimensional NSCBC brought a drastic reduction of flow distortion and numerical reflection, even in the regions of strong transverse convection. The treatment for edges and corner boundaries with the combination of multidirectional characteristics and compatibility conditions yielded stable and accurate solutions.

Furthermore, it is now established in the literature that in LES approach, only larger energy-containing eddies are resolved and the effects of the smaller eddies are modelled using a Sub Grid Scale (SGS) model. Also, all the previous LES studies on jets have utilized the linear SGS model, which is isotropic in nature. However, for the free jetmodelling the shear action and mass engulfment between the jet core and the ambient fluid are unstable and anisotropic. Therefore, to enable adequate modelling of turbulence anisotropy and energy backscatter, the use of more complex non-linear SGS models seems to be sensible. Hence, to compare the efficacy of LES of subsonic plane jet (at Re = 4000), using both linear and non-linear SGS models, the centreline velocity decay, jet spreading rate, mean velocity distributions and turbulence intensity distributions were investigated by Liu, et. al (2008) [31]. In this study, the researchers compared the results of mixed-non-linear SGS models namely, Kosovic (1997) [32], Leray (1934) [33] and Lagrangian Averaged Navier–Stokes 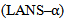(2001) [34] with the Smagorinsky (1963) [35], and Yoshizawa (1993) [36], linear SGS models. The effectiveness of all these five numerical methods, in predicting the jet flow characteristics were also compared with the Direct Numerical Simulation (DNS) and experimentaldata. They observed that except for 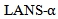model, where the small scale vortex stretching is supressed, the difference in results obtained with the other models were insignificant. Therefore, the researchers established that corrections in the basic LES models do not show a clear improvement.

1.4. Direct Numerical Simulation (DNS) of Jet Flows

The Direct Numerical Simulation (DNS) technique involves the direct solving of the the Navier–Stokes equations numerically, without using any turbulence model. This essentially means that the whole range of spatial and temporal scales of the turbulence must be resolved. All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales (Kolmogorov microscales), up to the integral scale L, associated with the motions containing most of the kinetic energy. The DNS is then most accurate of all the available numerical schemes. A survey of DNS research, as applied to turbulent jet flows is documented here. In a recent review by Ball et al (2012) [37], many issues related to simple turbulent round jets were studied both computationally and experimentally. The role played by complex mathematical approaches such as LES and DNS on the effects of Reynolds number, inlet conditions (excluding swirl) were extensively detailed, considering both near and far field investigations. They found that the investigation of the structure of turbulence in a jet depended increasingly on DNS, whose application is being pushed to ever higher Reynolds numbers. They also stated that the initial conditions (inlet conditions) of the jet flows are carried through to the far field affecting the jet development and structure. For better understanding of the flow field, they proclaimed that the study of structures, energy, and modes are of vital importance. However the authors did not focus upon some of the vital parameters including the thermo-physico-chemical effects (such as density variation, heat release), the effects of passive or active control, scalar contaminant transport and the jets operating in the absence of any geometric modifications to the nozzle (such as lobes, tabs). The three dimensional spatially evolving turbulent jets were numerically computed using DNS of the compressible Navier-Stokes equation and validated with the available experimental data by Stanley et al (2002) [38]. DNS with high-order space and time accuracy and appropriate schemes to handle inflow and outflow boundaries were claimed to successfully represent a spatially evolving plane jet in this work. The evolution of mixing process in turbulent planar jets are characterized by the probability density functions for the passive scalar. They proposed that in the core of the self-similar region of a fully turbulent jet flow the mixing process is dominated by small-scale mixing whereas, near the jet edges the engulfment of co-flow fluid is predominately done by the large scale structures. They showed that the development from interacting shear layers near the nozzle to the self-similar jet can be captured, albeit at a moderate Reynolds number. Gohilet al (2012) [39] adopted the DNS approach for various low Reynolds number flows through circular jets, in order to understand the instabilities associated with them. They obtained the critical Reynolds number from the perspective of unsteadiness of axisymmetric shear layers within the computational domain. When the Reynolds number was increased above the critical value, the mode changed from helical to axisymmetric. They introduced a small amount of perturbation in the flow in the form of noise, which had a profound effect on the entrainment rate, jet half-width and the vorticity thickness. However, it was seen that beyond 3% perturbations made flow to be turbulent throughout. The DNS numerical approach was implemented to calculate the complex shear flows such as jet evolving from a modified nozzle exit, for the prediction of flow structures and noise characteristics with acceptable accuracy. Freund and Moin (1998) [40] used DNS to study the effect of low Reynolds number fluidic actuators at the nozzle lip in forcing a Mach 0.8 jet. Here instead of simulating them explicitly, they simulated the actuators and the main stream nozzle by adding ‘source’ terms to the compressible form of Navier-Stokes equation and passive scalar transport equations. They visualized the vorticity magnitude contours for the unforced and forced shear layers. Observations indicated that under forced conditions, the jet spreaded quickly in the plane containing the actuators, unlike in the plane perpendicular to it. The plot of centerline velocity for the unforced and forced cases showed the decrease in core length in the forced case (almost half that of the unforced case). The forcing frequency was not varied in this work. The quantification of the heat radiated in both the cases made them conclude that the mixing was pronounced more in forced jet case. Further, they also observed a small amount of reverse flow near the nozzle lip in the forced case, which was not clearly explained.

DNS for the vector controlled jets for improved jet mixing was studied by Tsujimoto et al (2011) [41]. They oscillated the inflow jet periodically at an oscillating angle of 5° perpendicular to the jet axis and varied the oscillating frequency from St = 0.01 to 0.4, in steps. The visualization studies of the instantaneous vortical structures showed the exhaust jet, which exhibited three modes: Wavy mode (St=0.01), Bifurcating mode (St=0.04) and Flapping mode (St=0.4). The centerline velocity and the turbulent kinetic energy (TKE) for the three modes were processed and the jet mixing characteristics were quantified using passive scalar, statistical entropy along with fluctuational statistical entropy. The researchers suggested that, the mixing efficiency was improved for the flapping and bifurcating modes as compared to their uncontrolled counterpart. The active control of jet using fluid injection was simulated by Lardeauet al (2002) [42]. They used DNS numerical scheme with realistic inflow conditions to analyze the performance of low Reynolds number jet mixing in the presence of two secondary control jets with 10% mass flux of the main jet was oriented at 45° angle inward to the main jet. They studied four cases by inducing swirl, pulsed and non-pulsed with control jets in- and out-of-phase with the main stream. They carried out vorticity visualizations and plotted the fluctuating kinetic energy and also recorded the effects of the controls on the mixing properties of the main flow, by solving a passive scalar equation. A rapid decrease in the mean longitudinal velocity was observed in the case of pulsed control jet with no swirl present in phase with the primary jet. They observed that the use of swirl effects and phase changes were the least favorable. It was also found that the pulsed secondary jets enhanced the rapid mixing in the main flow as compared to other cases.

Tsujimotoet al (2006) [43] simulated the mixing enhancement in the parallel jets and combined jets in subsonic regime using DNS by varying the angular inclination of the jets having a fixed distance between them. A hybrid scheme of sixth order in the axial direction and the Fourier series in the azimuthal direction was adopted in domain discretization. The vortices produced by the different cases of unexcited and excited jets are quantitatively and qualitatively visualized by DNS and the acquired turbulent intensity and velocity decay plots were compared with available experimental data. The parallel jets with varying distances were simulated and it was found that these were ineffective in efficient mixing since the interaction of the two jets begins at a far downstream location where the vortex break down takes place and up to which the parallel jets behaves as individual jets. The flow visualization of the inclined jets and their streamwise velocity contours showed that the impingements causes the abrupt generation of fine scale vortices irrespective of the inclination angle and the presence of large scale vortical structures before impingement. Enhanced mixing was observed in case of combined jets with low angle of inclination. DNS for pulsed jets low Reynolds number jets was developed by Mouldonand Acharya (2010) [44]. They performed simulation by varying the pulsing frequency of the jet characterized by Strouhal number (≈ 0.2, 0.4and 0.6) for sine wave and compared it with the unpulsed cross jet. The visualization of the wake vortices, velocity vectors, temporal frequency spectra and jet trajectories for all the pulsed and unpulsed cases showed that the pulsing greatly increased the jet spreading rate and enhanced mixing properties of the jet. At St=0.6, in addition to efficient lateral penetration of cross-flow into the jet, they observed the elimination of wake vortices in the jet. A significant asymmetry was observed in the flow at St=0.2. However, the unpulsed cases were also not clearly explained by the authors.

Silva and Metais (2002) [45], conducted a DNS and LES on high Reynolds numbers (ranging from 1.5x103 to 5.0x104), bifurcating jets to study their vortex dynamics under excitations. They used incompressible Navier-Stokes equation considering the flow as incompressible and an active control of the inlet conditions is favored to the jet spreading in one particular spatial direction, thus creating a bifurcating jet. In this study, three types of forcing were superimposed with the inlet condition, which includes: flapping in preferred mode, flapping in sub harmonic mode and varicose mode (St = 0.38). These were simulated and compared with the unforced natural jet. The instantaneous vortical structures for all the forcing excitations were visualized and analyzed in detail. The effects of Reynolds number and excitations on the bifurcating of jets were also analyzed and it was concluded that an inlet excitation that combines an axisymmetric excitation at the preferred frequency (called flapping excitation at the sub-harmonic frequency), was the most efficient strategy for jet control, even at high Reynolds numbers. Klein et al (2003) [46] investigated the influence of the Reynolds number on the evolution of a subsonic plane jet by addressing the effect on the global jet characteristics. They succeeded in finding that the flow is dependent on the Reynolds number, and they also observed that the jet is close to convergence at higher Re values They also studied the influence of the inflow boundary conditions on the jet characteristics and found that the effect on the flow is very strong and long living throughout the computational domain of the jet.

From the above studies, it is seen that the turbulent jets of various configurations were tested using DNS approach in recent past. Balaracet al (2005) [47], performed DNS and LES studies of the coaxial jets and studied the influence of Reynolds number on coherent vortices and jet mixing. Reynolds number was varied; for lower Reynolds number ( ≈ 3000), DNS approach was adopted, whereas large eddy simulation was carried at higher Reynolds number (6000, 10000 and 30000) for annular to core flow velocity ratios of 5 and 17. At lower Reynolds numbers, the vortical structures appear downstream, whereas an increase in Reynolds number leads to appearance of these structures right in front of the nozzle lip. At annular to core flow velocity ratio of 17, they observed the formation of recirculation bubble, which at higher Reynolds numbers, was recorded to exhibit decreased size and non-stationary characteristics. The researchers from the results of DNS concluded that the recirculation bubble ensures early turbulent activity and also enhances mixing characteristics even at the beginning of the jet itself. Muppidi and Mahesh (2008) [48] used DNS to study passive scalar transport and mixing in a low Reynolds number rounded turbulent jet placed in a laminar cross-flow. The ratio of jet centerline velocity to cross-flow velocity of 5.7 with a Schmidt number of 1.49 in the scalar field was used to compute entrainment of the cross flow fluid by the jet. Also, interestingly, the transverse jet was found to entrain more fluid than a regular jet even when the jet was not yet bent into the cross flow. Here, the transverse jet’s enhanced entrainment was explained in terms of the pressure field around the jet. The acceleration imposed by the cross-flow deformed the jet cross-section on the downstream side, inducing a pressure gradient that drives downstream cross-flow fluid toward the jet. The simulation results were used to comment on the applicability of the gradient diffusion hypothesis to compute passive scalar mixing in this flow field. Computed values of the instantaneous contours of passive scalar, scalar flux, entrainment plot and eddy diffusivity showed significant scatter and pronounced anisotropy. The near field also exhibited counter gradient diffusion.

The passive control of jets using DNS approach was found to give results with exceptional accuracy for various control devices. Caiet al (2010) [49] performed numerical simulation using DNS method and conducted experiments to compare the mixing characteristics of circular nozzle, V-shaped notched nozzle and an A-shaped notched nozzle of same circular cross-sectional area. The dye visualization technique revealed that in addition to azimuthal vortex rings created because of the shear-layer, the stream-wise vortex pairs (both inside and outside the vortex rings that spread outward as the vortex rings move downstream) greatly enhanced the entrainment and mixing of the ambient fluid with the jet core. It was seen that the production of stream-wise vortex pairs for the notched circular nozzles owned peak and trough locations unlike their circular counterpart. They concluded from the results of instantaneous vorticity visualisations that the mixing characteristics of the three types of nozzles is such that the jet spreads faster in the peak-to-peak and trough-to-trough cross-planes than in other directions. Thus, the notches in the nozzle exit significantly enhanced jet mixing as shown by the centerline velocity decay plot. In contrast to the RANS and LES approaches, direct numerical simulation (DNS) methods successfully provided the entire turbulent energy spectrum by resolving all turbulent scales ranging from integral length scale down to the Kolmogorov scale. Although this avoids the limitations associated with turbulence modeling, DNS methods may remain computationally impractical in the foreseeable future for all but the simplest configurations.

Rembold et al (2002) [50] performed the DNS simulation of a Mach 0.5 jet exiting from an aspect ratio 5 rectangular nozzle at Re = 2000. For spatial discretization, they used the 5th order compact upwind biased scheme for the convective terms and a 6th order compact central scheme for the diffusive terms. They triggered the transition process by the most unstable symmetric linear Eigen mode of a parallel laminar jet profile at the nozzle exit. They observed the transition process, in which the initial 2-dimensional disturbances in the inflow region of the laminar jet rapidly resulted in 3-dimensional turbulence. The shear layer roll-up for the laminar jet and a subsequent rapid transition to small-scale turbulence was observed from the instantaneous and statistically averaged results. Because of vortex shedding from the jet periphery, the symmetrical rectangular jet cross-section got distorted to an elliptic cross-section. Furthermore, it is understood from the vortex theory that size of a vortex is propotional to the radius of curvature of the surface from which it is shed. Since the relatively larger eddies are shed along the major axis and smaller ones along the minor axis, the jet spread rate was found to be rapid along the major axis direction due to higher mass engulfment. This diffrenetial rate in spreading leads to rotation of axes known as ‘axis-switch’ as shown in Figure 3.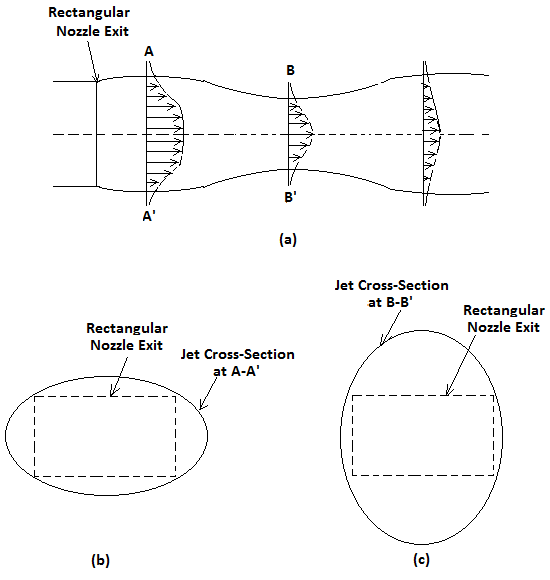

Figure 3. A typical schematic diagram of ‘axis-switch’ phenomena

The impingement of a high velocity jet on an object was studied extensively by the researchers due to their wide applications including the rockets and vertical take-off and landing (VTOL) aircrafts. A typical schematic of the impinging jet is shown in Figure 4. The fluid stream at a high velocity and thus with ahigh kinetic energy, issuing from a nozzle or orifice is made to impinge on a plate or an object. The characteristics of these jets involve complex flow evolution and interactions due to the vorticity and turbulence dynamics. Because of these factors, the numerical modelling of the impinging jet becomes a challenging task. Further, it is also seen that in all the previous studies reviewed, DNS of ‘cold-jets’ was performed and the heat transfer aspects were not considered. Hattori and Nagano (2004) [51] computed the plane turbulent impinging jets with heat transfer using DNS. The flow characteristics and turbulence statistics, along with the heat transfer data were obtained to understand the influence of the nozzle exit to plate distance (H) on the impinging jet. They found that the local heat transfer rate (in terms of the Nusselt number) increased with a decrease in ‘H’ and also observed the presence of second peak in the developing region of the wall jet for lower values of ‘H’. It was also seen that the turbulence intensity in the direction normal to the wall was promoted in the near wall region.

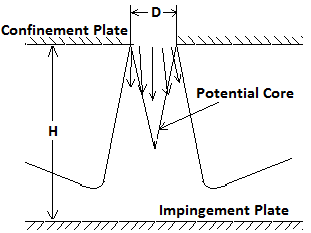Figure 4. Schematic diagram of a jet impinging on a flat plate

2. Conclusions

With the advancement of computational resources, the reserachers in the jet field have performed analysis using various numerical schemes such as, Reynolds Averaged Navier-Stokes equation (RANS), Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS) in simulating jets. All the approaches have their own merits and demerits. It was found that RANS approach is having serious limitations for jets with significant three-dimensionality, compressibility effects and high temperature streams. The implementation of correction factors to the RANS approach in general improves the accuracy of the mean velocity field and quantities such as potential core length, but they still suffer from inaccuracies in the prediction of turbulent kinetic energy fields. Though LES approach has delivered results with good accuracy, this approach has also been found to result in errors in treating complicated flow structures. Further, the researchers investigated the DNS approach to calculate the entire turbulent energy spectrum by resolving all turbulent scales down to the Kolmogorov scale. However from the standpoint of the availability of computational resources, the DNS approach suffers from being computationally intractable for high Reynolds number cases and realistic geometries. Even with the sky rocketing advances in today’s technology, the DNS scheme with extreme requirements on grid resolution and resulting computational expense is not viable for realistic geometries and flow conditions in the foreseeable future.

The LES method offers a good trade off between accuracy and computational efficiency. It is clear that the LES based methods surpass the accuracy of RANS for most of the problems. In addition, LES provides accurate unsteady turbulent information, which RANS approach fails to provide. However, there still exists a barrier to utilise LES, instead of RANS, as the method of choice for complex jet flow field analyses. For example, since the computational cost of LES is much higher than RANS, most LES studies have focussed on simple configurations such as round jets. The hybrid RANS/LES approach may be an efficient tool in predicting the flow field by combining the advantages of both RANS and LES schemes. But it still has limitations due to complex grid topologies at the interface. These methods must be extended to handle complicated grid schemes in order to make LES viable for future work. As we gain a better understanding of the various components that make up a LES simulation and as computing power increases to accommodate higher resolutions, LES will become an ideal tool for jet flow simulations in future.

ACKNOWLEDGEMENTS

The authors acknowledge the financial support provided by Sponsored Research and Industrial Consultancy (SRIC), Indian Institute of Technology, Kharagpur in order to complete the present investigation.

Nomenclature

AR = Aspect ratio

D = Diameter of the nozzle exit

DNS = Direct Numerical Simulation

f = Frequency

H = Nozzle exit to plate distance for impinging jet

LES = Large Eddy Simulation

PLIF = Planar Laser Induced Fluorescence

M = Mach number

Nu = Nusselt number

R = Jet radius

RANS = Reynolds-Averaged Navier-Stokes

Re = Reynolds number

SGS = Sub-grid scale

St = Strouhal number

U = Jet velocity

X = Location in axial direction

θ = Shear layer momentum thickness

ILES = Implicit SGS model – LES