1. Introduction

Air quality is one of the fundamental prerequisites for a high living standard, however, technological developments and their use by the society point into the opposite direction. Progress goes hand in hand with an increase in anthropogenic sources, such as power plants, manufacturing facilities, transport and many others. Interference of mankind in the environment has taken influence even on natural sources like dust, methane, smoke from wildfires and even geological events.

Decisions that shall limit pollution are of political nature and thus do not obey physical laws and are consequently less predictable than the physical process of pollution transport in the habitat. Nevertheless, pollution dispersion is still a phenomenon with open questions, so that there is need for experiments, modeling and simulations. The present contribution is an attempt to head into a new direction. While most of the models that are used as references for licensing and commissioning of industrial installations are of deterministic character, whereas pollution generation and transport are clearly stochastic processes. In deterministic models the micro-meteorological properties are usually parameterized such as to idealize the effects of mixing of pollutant substances with air in the planetary boundary layer. There do exist stochastic models, but micro-meteorological properties are less detailed than in deterministic approaches.

Hence, a new attempt with deterministic-stochastic structure could combine the advantages of deterministic models, while at the same time providing properties of higher statistical moments that characterize stochasticity instead of implying additional models for each statistical moment. To this end we start from a deterministic model, more specifically the advection diffusion equation, that is based on the continuity equation together with a Fickian type closure. Since the Fickian closure renders the model a deterministic one we propose a complex turbulence diffusivity that accounts for the presence of a phase and interpret the solution of the complex advection diffusion equation in terms of an amplitude that upon multiplication with its hermitesch conjugate defines a density function in sesquilinear form. Such a procedure does already exist for instance the energy density in electrodynamics or the probability density function in quantum approaches.

We present a selection of simulations in order to explore the effects of the complex turbulent diffusion parameterization on the distribution pattern of the concentration distribution. These studies shall open pathways to understand how to determine the coefficients from observational data.

2. The Model

The most studied analytical model of pollutant dispersion is the advection-diffusion equation [3] where simplifications as Reynolds averages and Fickian closures are applied so that a solution can be easily obtained. The equation is given by

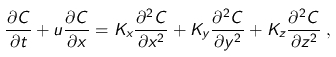where C[g/m] is the concentration, u[m/s] the wind speed along x[m] and the K's[m 2 /s] are the diffusion coefficients in the respective spatial directions, with the initial conditions: zero flow at the boundaries; zero concentration at t=0; and three punctual time-continous sources aligned along the y directin with a distance of Δy = 0.1[m] between neigbours and H_s is font height .

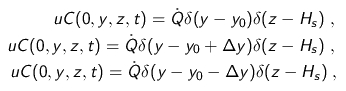To represent some characteristics of the turbulent phenomenon we propose the inclusion of a phase in the three-dimensional and transient advection-diffusion equation, since (ECs) phase dominated turbulent characteristics. Thus the advection-diffusion equation is solved and a solution was obtained including the afore mentioned modification of Fickian closure by replacing the diffusion coefficient K_z by a complex diffusion coefficient and presenting the pollutant distribution in sesquilinear form [4]. A complex constant can be represented by K_z = K_za + iK_zb , where K_za is the real part and K_zb the imaginary. This complex coefficient makes the solution of the advection-diffusion equation complex, I.e. the solution is in the body of complex functions with module and phase. The distribution of the concentration must be real and semi-positive definite, where in analogy to electromagnetic phenomena [5], where the energy density is described in a sesquilinear form in terms of the electric field, we propose a sesquilinear density function that represents the pollutant distribution. Consequently the solution generates a semi-positive non-linear distribution thus returning a qualitative characteristic present also in eddy covariance procedures.

Then multiplying the complex solution C (x, y, z, t) by its complex conjugate solution C *(x, y, z, t) yields

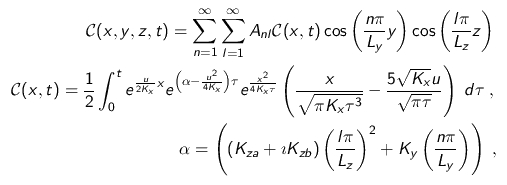where the difference is that K_z∗ = K_za - iK_zb.

3. Results

A series of spacial and space-time distributions were compared with distribuitons with real diffusion coefficient only but in the same conditions as in figures 1 and 2. The model is capable of reproducing these results without turbulent behavior by using a complex coefficient with imaginary part zero.

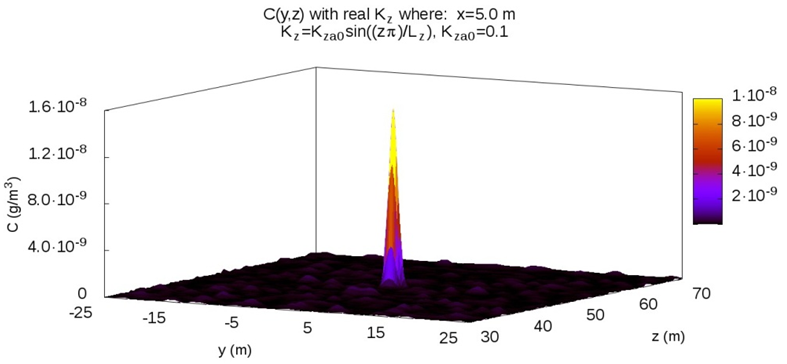Figure 1. Distribution C(y, z) with Kz real

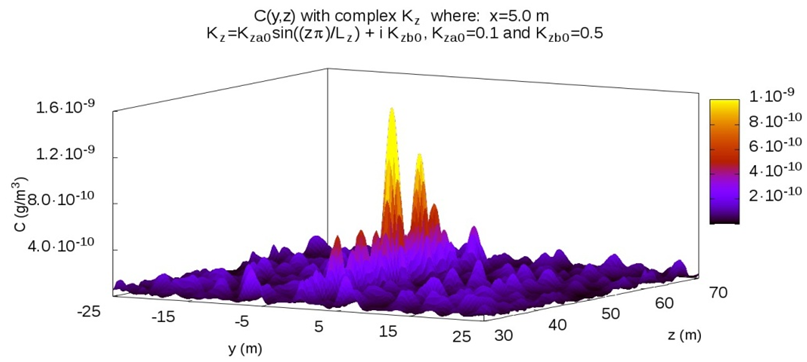Figure 2. Distribution C(y, z) with Kz complex

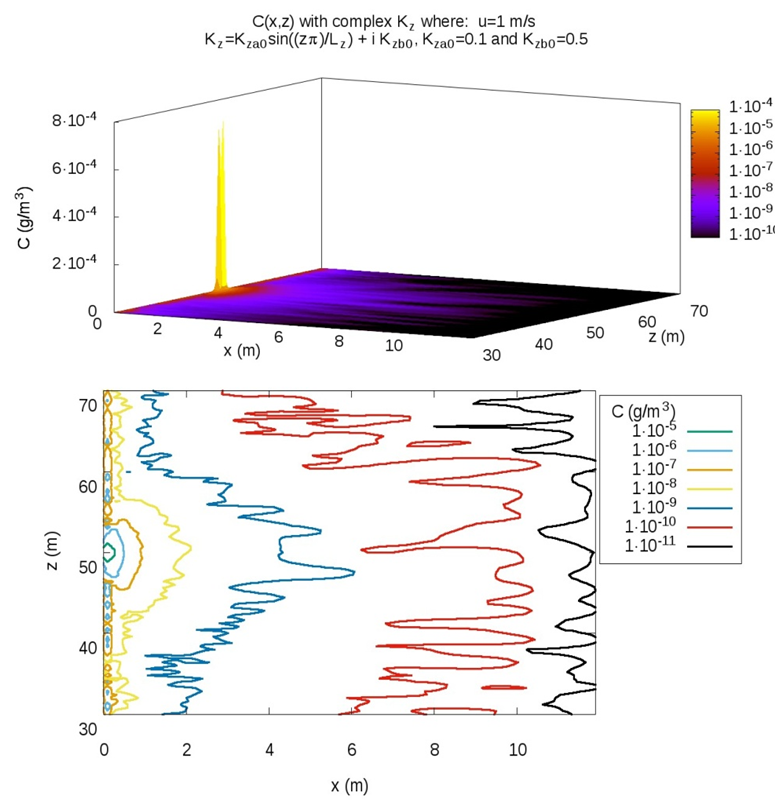Figure 3. Distribution and Map of concentration in C(x,z) with low wind speed

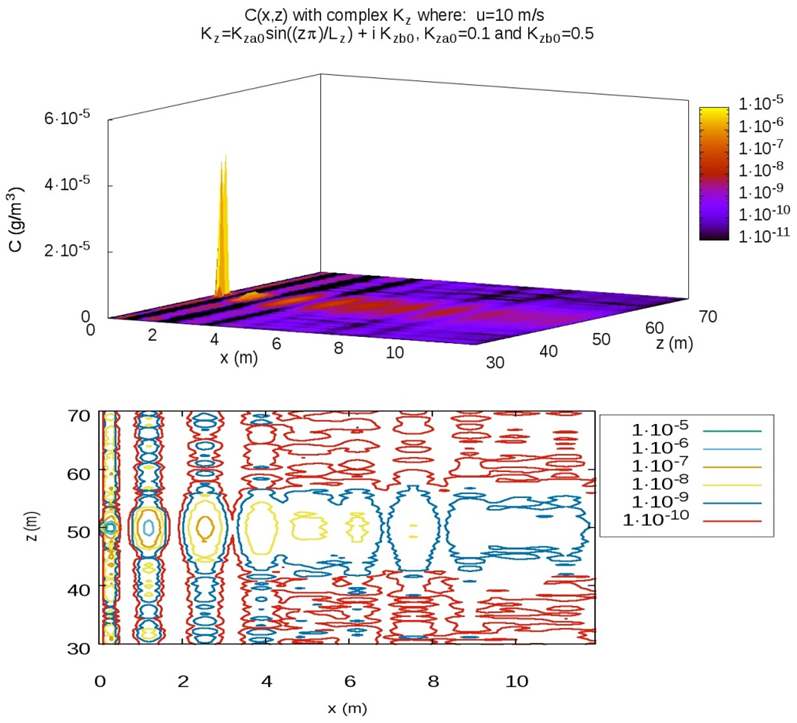Figure 4. Distribution and Map of concentration in C(x,z) with high wind speed

It is noteworthy, that up to now there is no unique prescription as how to determine the parameters of the model to represent physical phenomena. Hence, as a state of the art of the developments we generated solutions with a variety of imaginary parts of the diffusion coefficients. Thus, the solution behavior is evaluated by varying the imaginary part of the diffusion coefficient, where one observes a broadening of the distribution together with oscillations which is driven by the increase of the coefficient in the real case where the higher the diffusion coefficient is the greater is the dispersion.

Morover a meander like behavior is observed in the distribution and map 3, where in low wind conditions and close to the source the dispersion of pollutants is irregular and inpredictable, where the plume is subject to horizontal waves across the wind direction, that was also detected in reference [6]. This phenomenon is not observed in the distribution and map 4 for strong wind conditions.

4. Conclusions

In the present work we studied a new conception for pollution dispersion that makes use of a sesquilinear representation of the concentration probability density function. Such a construction allows to extract besides average values also higher statistical moments from one unique solution. The presence of a phase introduces fluctuations in the distributions that are also observed either visually or in dispersion measurements. It is noteworthy, that with only a few parameters it is possible to describe rather complex distributions which in the present work are still quantitative. Though, in future studies these will be adjusted such as to reproduce at least the four statistical moments, mean, variance, skewness and kurtosis in comparison to experimental data. The present discussion is thus a first step into this direction.

ACKNOWLEDGEMENTS

This work was supported by Linhares Geração SA, Tevisa and ANEEL P&D.