1. Introduction

The dispersion of contaminants in low wind speed conditions in the Stable Boundary Layer (SBL) represents a difficult physical problem as the occurrence of meandering winds do not allow traditional dispersion models to simulate adequately the contaminant concentration. Thus, it is essential to develop new parameterizations that describe such processes as they are observed in the atmosphere [1, 2]. In situations in which the wind mean velocity is small, the horizontal wind direction is subject to large variations. Therefore, it is not possible to determine a preferential direction [3, 4]. In these conditions, the large horizontal wind oscillations of low frequency, called meandering, spread the contaminants over a rather wide angular sector, which reinforces the horizontal transport of contaminant [1, 5]. Consequently, the meandering phenomenon needs to be incorporated in the simulations of the contaminant dispersion [6, 7]. In this particular case, the Lagrangian models are considered the more indicated, because they describe appropriately the dispersion process during the presence of the meandering. Furthermore, in these models it is possible to incorporate, in a more simple way, temporal and spatial variations in turbulence properties in relation to other techniques, such as similarity or gradient-transfer theory [8, 9].

In this study we employ the model ILS-LW [8] to simulate the enhanced meandering dispersion. The meandering loop parameter 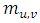and meandering period 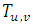used in this simulation are obtained from observational data measured in Brazilian Amazon Region [4].

The performance of the ILS-LW model using the meandering parameters proposed by Moor et al. [4] is validated considering the values of ground-level concentrations measured during the experiments of the Idaho National Engineering Laboratory (INEL) [10]. In addition, we present a statistical analysis to evaluate the simulation with new meandering parameters in comparison with the observed concentrations [10].

In Section 2 we present the Langevin model, in Section 3 the meandering parameters employed in the simulations and in Section 4 the results are discussed.

2. Lagrangian Stochastic Particle Model

Lagrangian stochastic particle models are based on Langevin equation [11], where the particle turbulent velocity is given by the combination between a deterministic term 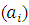and a stochastic term 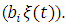The velocity and the position of each particle, in each time, are obtained from the numerical integration of the equations:

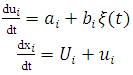(1)

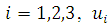where is the turbulent velocity, 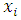is the displacement, 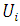is the mean wind velocity. The method applied solves the Langevin equation (Eq. (1)), in a semi-analytical manner, using the method of successive approximations, or Picard’s Iterative Method [8].

3. Experimental Physical Parameters of the Horizontal Wind Meandering

[4] presented a new autocorrelation function to study horizontal wind meandering. From a dataset measured in Brazilian Amazon region, they obtained an experimental fitting that allows to calculate the meandering time scale and the loop parameter magnitudes for low wind speed in a nocturnal stable layer (Table 1).

Table 1. Meandering period and loop parameter average values for the u and v components by [4]

The autocorrelation function proposed in [4] considers cases in which turbulence coexists with low-frequency motion associated to the meandering phenomenon. The expression is provided by

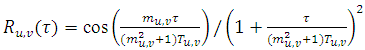(2)

Equation (2) can also be written in a different manner, namely

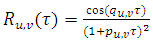(3)

with

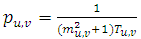(4)

and

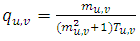(5)

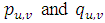are hybrid quantities described in terms of the time scale for a fully developed turbulence 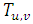and a non-dimensional quantity that controls the meandering oscillation frequency 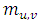associated to large oscillation of the horizontal wind [1, 12, 13]. This autocorrelation function generates a negative lobe for the horizontal wind components attributed to the meander [1, 4].

4. Results and Discussions

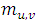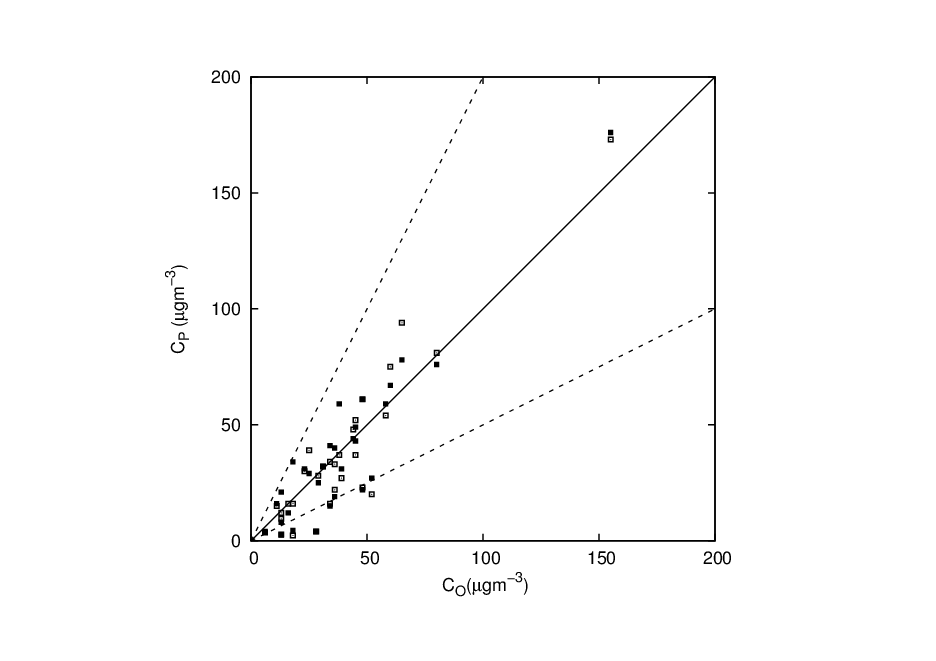
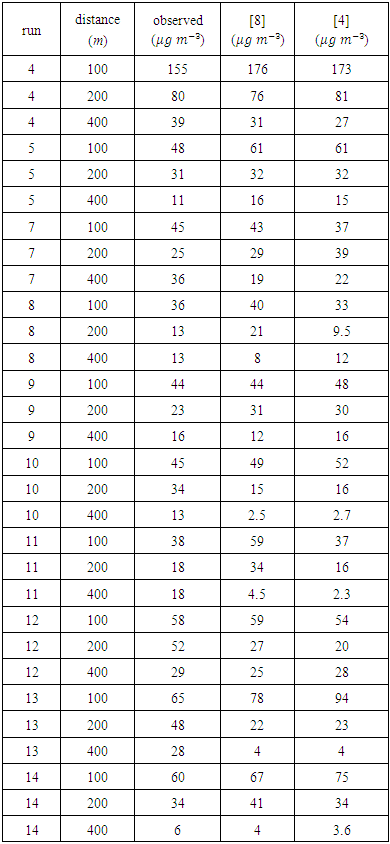
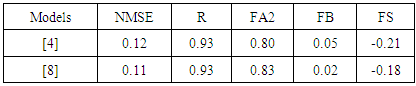
In the simulations the mean values of the loop parameter and the meandering period 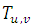(Table 1) were employed in the ILS-LW model [8]. The results are compared with concentrations measured data in the Idaho National Engineering Laboratory (INEL) [10]. Furthermore, the concentrations data from our simulation are compared with the simulation performed by [8]. Table 2 shows the comparisons between the simulated concentration data and observed concentrations data.

Figure 1 represents the scatter diagram between observed and predicted ground-level concentrations. The scatter over the central line shows that new parameterization to the meandering loop parameter and the meandering period inserted in this model reproduces satisfactorily the experimental data in low wind speed conditions. Furthermore, the concentrations simulated values are similar with those obtained by [8].

Figure 1. Scatter diagram between predicted (Cp) and observed ground-level concentration (Co) for the INEL experiment. The solid squares represent the concentrations by [8] and the open square the new parameterization proposed by [4]

These results show the importance of considering the parameters related to meandering in the simulations of the contaminant dispersion. The data between two dashed lines are in a factor of 2 (0.5 ≤ C_o/C_p ≤ 2) with C_p the predicted concentration and C_o the observed ground-level concentration for the INEL experiment.

Table 2. Comparison between observed concentration and measured during the INEL experiment and predicted values from [8] and [4]

Table 3 presents an analysis based on statistical indices [14]. The small positive values of statistical index FB, suggest that the models underestimate the mean observed concentrations. The FS indicates that the dispersion of the mean simulated concentrations overestimates the experimental data. Other indices, such as NMSE and FA2, are similar for both cases and it is an indication of a good agreement between models and observations. Furthermore, the correlation coefficient R, positive and near one, indicate that there is a good correlation between the observed and simulated values.

Table 3. Statistical evaluation of the proposed simulation and [8] model with observed values

5. Conclusions

In the low wind stable boundary layer, the contaminant dispersion is directly influenced by the meandering phenomenon, which is characterized by low frequency horizontal oscillations of horizontal wind. Therefore, the results of simulations accomplished during low wind speed periods depend of the meandering parameters inserted in the dispersion models.

For the meandering dispersion we employ the meandering period and the loop parameter obtained from experimental data measured in Brazilian Amazon region in the ILS-LW model to simulate dispersion of contaminant.

The concentrations obtained with the new observational meandering parameters were compared with the concentration measured data in the Idaho National Engineering Laboratory (INEL). The results presented and discussed are in agreement with experimental values found in the literature.

ACKNOWLEDGEMENTS

The authors would like to thank the CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) and Capes (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior) for partial financial support of this work.