-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2015; 5(1A): 106-118
doi:10.5923/s.ajee.201501.14
Comparison of Mixing Length Formulations in a Single-Column Model Simulation for a Very Stable Site
Moacir Schmengler 1, Felipe D. Costa 2, Otávio C. Acevedo 3, Franciano S. Puhales 3, Giuliano Demarco 3, Luis Gustavo N. Martins 3, Luiz E. Medeiros 3
1Centro de Previsão de Tempo e Estudos Climáticos, Instituto Nacional de Pesquisas Espaciais, Cachoeira Paulista, SP, Brazil
2Programa de Pós-Graduação em Engenharia, Universidade Federal do Pampa, Campus Alegrete, RS, Brazil
3Departamento de Física, Universidade Federal de Santa Maria, Santa Maria, RS, Brazil
Correspondence to: Otávio C. Acevedo , Departamento de Física, Universidade Federal de Santa Maria, Santa Maria, RS, Brazil.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Reproducing the behavior of the mean variables that control the nocturnal atmospheric flow under very stable conditions is a very difficult task for atmospheric models. To understand the role of the surface scheme, turbulence scheme and radiation scheme on the performance of a single column model, its predictions are compared to observations collected at a very stable site located in deforested region in Amazon. The surface scheme takes on consideration the rapid changes in the surface energy budget caused by the presence of a vegetated layer over the soil. The turbulence scheme uses four different formulations for the mixing length. Two of them allow the existence of turbulence over the critical Richardson number, while the other two restrict dramatically the turbulence activity in those situations. The radiative scheme considers a clear sky condition, and evaluates the radiative flux divergence between 3 levels within the vertical domain: near the surface, at the domain top, and at the middle point between them. The predictions of all mixing length formulations are very similar to the observed data near the surface, indicating that in this region the surface plays a crucial role. At upper levels the most turbulent formulations lead to better results. This is a consequence of atmospheric decoupling when the turbulence is completely suppressed, which leads to colder results near the surface and warmer results aloft. The radiative scheme reproduces quite well the temperature decay above the boundary layer for all cases, in spite of its simplicity. On the other hand, the comparison between modeled and observed humidity profiles shows that it is necessary to improve the model by including a more complete scheme for humidity and by adding a advection scheme to it.
Keywords: Very Stable Boundary Layer, Atmospheric Modeling, Mixing Length Formulations
Cite this paper: Moacir Schmengler , Felipe D. Costa , Otávio C. Acevedo , Franciano S. Puhales , Giuliano Demarco , Luis Gustavo N. Martins , Luiz E. Medeiros , Comparison of Mixing Length Formulations in a Single-Column Model Simulation for a Very Stable Site, American Journal of Environmental Engineering, Vol. 5 No. 1A, 2015, pp. 106-118. doi: 10.5923/s.ajee.201501.14.
Article Outline
1. Introduction
- Numerical models often have difficulties for properly representing turbulent fluxes in the nocturnal boundary layer. In particular, the model performance is highly variable among different nights, and the main factor controlling this variability is the nocturnal stability regime. The stable boundary layer (SBL) has been classified in weakly stable or very stable [1, 2] or, alternatively, in terms of the coupling state between the surface and the upper levels, in coupled or decoupled [3, 4]. The weakly stable regime is characterized by continuous turbulence and generally occurs in windy nights. In this case, turbulence exists throughout the vertical extension of the SBL, characterizing a coupling between the surface and the upper boundary layer. In this case, similarity relationships are valid, and mean boundary layer variables may be predicted in a satisfactory manner by numerical models (e.g. Delage [5]; Wyngaard [6]; Duynkerke and Driedonks [7]; Cuxart et al. [8]; Steeneveld et al. [9]; among many others). On the other hand, in nights with large radiative loss and calm winds, turbulence intensity is drastically reduced by the considerably larger thermal stratification. The fluxes, in this case, are damped by the intense stability, leading to a very stable SBL regime [1, 4]. Such a regime can be related with the decoupled SBL state, when turbulence is not vertically continuous, so that the bottom part of the SBL becomes disconnected from the upper levels. The controls of the transition between the two states are not well understood, but recently van de Wiel et al. [10] and van de Wiel et al. [11] investigated the turbulence collapse in the SBL using models based on similarity and bulk relationships, and showed that such a transition tends to happens with geostrophic winds ranging from 3 to 7 m s-1, values that are in agreement with those found by Acevedo et al. [4] using a very simple multilayer model.The difficulty in predicting the SBL behavior under very stable conditions is associated with the fact that, in this case, often similarity relationships and stability functions lead to exceedingly small surface fluxes, causing excessive quick air cooling and subsequent unrealistically low temperatures [12, 13]. Besides, the radiative flux divergence plays an important, non-neglectable role in such regime. For this reason, building a model able to perform well in both SBL regimes constitutes a major challenge for micrometeorological research. Different turbulence formulations have been used in operational weather forecast models worldwide. Cuxart et al. [8] compared the performance of some of them in a single column model with results from Large Eddy Simulations (LES) for a idealized case of nocturnal boundary layer with continuous turbulence [14], while Svensson et al. [15] compared the performance of the same formulations for a diurnal cycle of observations during the Cooperative Atmosphere – Surface Exchange Study (CASES-99), and again the nocturnal period was continually turbulent. Steeneveld et al. [9] used a single column model coupled to a modified version of the surface scheme introduced by Duynkerke [16] to simulate the behavior of the SBL regimes for three different nights of the CASES-99 experiment: one with continuous turbulence, the second with intermittent turbulence and the third one was a radiative night. Their results indicated some limitations of the model performance in the very stable cases (the intermittent and radiative nights) and in all cases their results confirmed the importance of properly resolving the processes happening at the surface.In this study, model outputs using four different turbulence formulations in a single column scheme are compared to observed data from eight nights, at a typically very stable site in a deforested region in Amazonia during the Large-Scale Biosphere-Atmosphere Experiment in Amazonia (LBA). The main purpose of the analysis is to provide a description of how these formulations perform in the very stable situation, which is most critical to their performance and, for this very reason, also the least studied condition. The analysis aims, therefore, at diagnosing the main problems of simulating the very stable surface layer by directly comparing model outputs to observations. The four schemes being compared differ in terms of the stability function used and on the method for representing the coupling between the surface and the atmosphere. The site and data are described in section 2. In section 3, the model, turbulence formulations and the surface scheme are described. The comparison between model results and observed data is presented and discussed in section 4. Finally, the conclusions are presented in section 5.
2. Site and Data Description
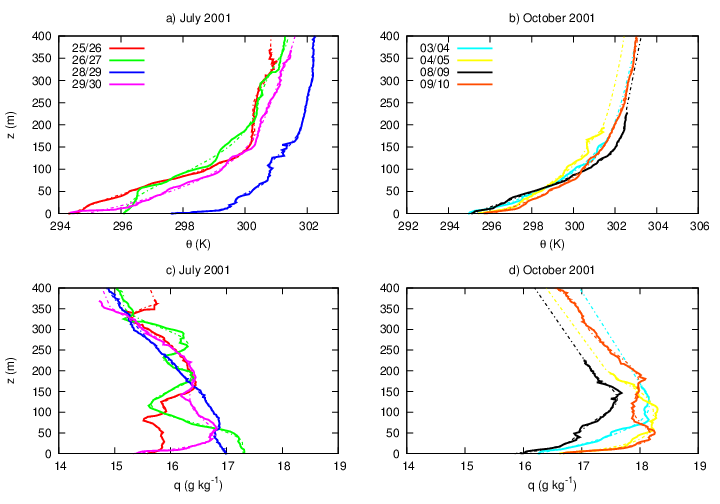
- The observations used in the present analysis have been taken at a deforested site in Amazonia. Excessive long-wave radiative loss at night make very stable conditions typical there. Tethered balloon profiles of temperature, humidity and wind speed and direction have been observed there during two campaigns, in July and October 2001. In each campaign, there are 4 nights of good quality data, during which different profiles are available for each night. More detailed information on the site are provided by Sakai et al. [35], while the campaigns are described by Acevedo et al. [36].For the period of analysis, observations of the soil temperature are available at five depths (0.14 m, 0.24 m, 0.50 m, 1.50 m and 2.00 m), while the soil heat flux was measured at two depths (0.19 m and 1.00 m) and the soil moisture content (θ) was observed at a 0.29 m depth. These data allow determining the soil thermal properties used in the present study. The local soil is a yellow latosol [35], whose median density under pasture regions in Alter do Chão Formation is ρ=1080 kg m-3 [37]. For the entire period, the best fit for median thermal conductivity is λ=0.25 W m-1K-1, and the soil volumetric heat capacity (Cv) has been evaluated following de Vries [38], as Cv=(ρ/ρm)Cm+θCw , where ρm, Cm and Cw are respectively the density and heat capacity of the mineral contents, and the water heat capacity. Asssuming that the mineral content may be approached as quartz, the values used for those quantities are: ρm=0.25 kg m-3, Cm=2.13 MJ m-3K-1 and Cw=4.18 MJ m-3K-1, leading to an estimated volumetric heat capacity of the soil of CV=1.73 MJ m-3K-1. Using the values of λ and CV in equation (17), one finds the thermal capacity per area unit of the slab to be Cg=5.18×105 J m-2K-1. As the value of the thermal conductivity is related to the volumetric heat capacity and to the apparent thermal diffusivity of the soil as λ=Cvk, the soil apparent diffusivity is k=0.144×10-6 m2 s-1.
3. Model
- The single-column model used in the analysis consists of two parts: an atmospheric scheme and a surface scheme. The atmospheric scheme considers a horizontally homogeneous ABL, and evaluates prognostic equations for the wind components, u and v, air temperature T and specific humidity q:
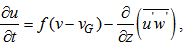 | (1) |
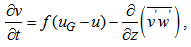 | (2) |
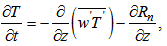 | (3) |
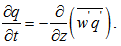 | (4) |
3.1. Turbulence Closure
- The turbulent fluxes are parameterized by K-theory as
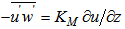 ,
, 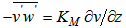 ,
, 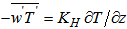 and
and 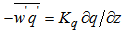 . The exchange coefficients for momentum heat and humidity are KM, KH and Kq, respectively. They are estimated by a 1.5 turbulence closure that relates them to the TKE (E) and momentum mixing length [7, 8, 17-21]:
. The exchange coefficients for momentum heat and humidity are KM, KH and Kq, respectively. They are estimated by a 1.5 turbulence closure that relates them to the TKE (E) and momentum mixing length [7, 8, 17-21]: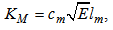 | (5) |
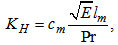 | (6) |
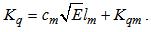 | (7) |
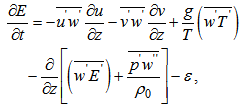 | (8) |
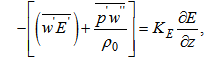 | (9) |
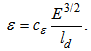 | (10) |
3.2. Mixing Length Formulations
- In Equations (5)-(7), the turbulence mixing dependence on stability is given by a prescribed stability function, which depends on local scaling parameters such as the Obukhov length L or the Richardson number Ri. Such function has direct influence in the turbulent mixing under stable conditions [5, 12, 26-29]. Four different formulations are used in the present study. Two of them use the Obukhov length L as stability indicator, while the other two use the gradient Richardson number for that purpose.
3.2.1. Mixing Length Formulations that Depend on L
- The first formulation used has been proposed by Delage [5] (hereafter DE74). In this formulation, the near-surface mixing length in neutral or stable conditions is directly proportional to κ(z+z0), where z0 is the roughness length, assumed as 0.1 m in the present study. The mixing length is limited by its value under neutral conditions
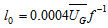 , or by κLβ-1, where β is a constant set as equal to 5. Therefore, the expression for the momentum mixing length under stable or neutral conditions is:
, or by κLβ-1, where β is a constant set as equal to 5. Therefore, the expression for the momentum mixing length under stable or neutral conditions is: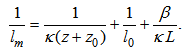 | (11) |
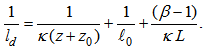 | (12) |
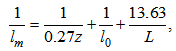 | (13) |
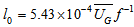 . For simplicity, when the formulation proposed by DG00 is used in the present study, the dissipation length scale (ld) is assumed to be equal to lm.
. For simplicity, when the formulation proposed by DG00 is used in the present study, the dissipation length scale (ld) is assumed to be equal to lm.3.2.2. Mixing Length Formulations that Depend on Ri
- Two other mixing length formulations are considered in this study. In both of them, stability is given by the gradient Richardson number, defined as:
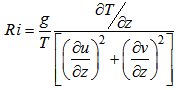 | (14) |
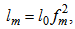 | (15) |
3.3. Surface Scheme
- When comparing mixing length formulations in a single-column model, it is usual to prescribe the surface cooling rate for the lower boundary condition [8]. In the present study, however, besides comparing such formulations, there is also the desire of understanding the role of surface parameterization under very stable conditions. For this purpose, and considering the site features, a scheme that solves both temperatures of the soil (Tg) and of a grass layer (Ts) that covers the surface was used [7, 9, 16].When a vegetated surface is considered, the surface temperature is evaluated through a slightly modified prognostic equation, which again considers the energy budget:
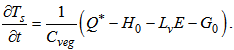 | (18) |
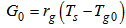 , where rg is the heat transport conductance between the vegetation layer and the soil surface, and Tg0 is the soil temperature at the surface. As observations of Cveg and rg are not available for the site considered, their values have been taken from the literature, from sites with similar characteristics: Cveg = 2.0×104 J m-2 K-1 [16] and 5.0 W m-2 K-1 [9, 34].To evaluate the soil temperature near the surface, an explicit scheme based on the diffusion equation has been used [9]:
, where rg is the heat transport conductance between the vegetation layer and the soil surface, and Tg0 is the soil temperature at the surface. As observations of Cveg and rg are not available for the site considered, their values have been taken from the literature, from sites with similar characteristics: Cveg = 2.0×104 J m-2 K-1 [16] and 5.0 W m-2 K-1 [9, 34].To evaluate the soil temperature near the surface, an explicit scheme based on the diffusion equation has been used [9]: 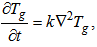 | (19) |
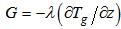 . In the former equation λ is the thermal soil conductivity. Following Duynkerke [16] and Steeneveld et al. [9], no explicit scheme for soil moisture is used here. The specific humidity at the surface is simply assumed to be the saturation specific humidity at the surface temperature.
. In the former equation λ is the thermal soil conductivity. Following Duynkerke [16] and Steeneveld et al. [9], no explicit scheme for soil moisture is used here. The specific humidity at the surface is simply assumed to be the saturation specific humidity at the surface temperature.3.4. Radiation Scheme
- Under clear skies, Swinbank [39] parameterized the air emissivity as εa=9.35×10-6 T2Ref, where TRef is the air temperature at a reference height, which should be higher than the region with intense temperature gradients. According to Acevedo et al. [36], there were no major synoptic events during the nights of data collection, so that a clear sky condition is assumed. It is not necessary, therefore, to evaluate the cloud contribution to the emissivity value [34, 40]. The reference height used here was zref = 200 m.The radiative flux divergence is evaluated from the long-wave emission at three different levels along the vertical domain: at the top of the domain (RTOP= εaσTTOP4 , zTOP = 400 m); at the reference level, in the middle of the domain (RRef = εaσTRef4, zRef = 200 m); and at the first atmospheric level, just over the surface (RS= εaσTS4, zS = 0.12 m) The radiative flux divergence can, therefore, be written as:
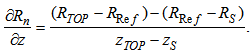 | (20) |
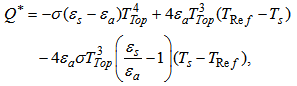 | (21) |
3.5. Grid Structure and Boundary Conditions
- Equations (1)-(4) are discretized using finite difference equivalents, in a stretched vertical grid. The stretched scheme used here has been proposed by Degrazia et al. [42]. Some modifications, however, have been made to improve the resolution at lower levels, so that strong gradients near the surface are properly resolved, and to provide enough resolution at the upper part of the domain. The vertical increment of the vertical grid is:
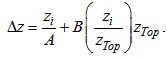 | (22) |
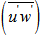 is set to be
is set to be  while all the other fluxes are assumed to be null at the start of the simulations.The initial conditions for temperature and specific humidity are taken from the first observation of each night, as shown in Figure 1 (solid lines). The initial values of both T(zi,t0) and q(zi,t0), have been obtained through a polynomial interpolation of the real data (dashed lines). For cases whose data do not reach the domain top, the function was just extrapolated up to the top (e.g. nights of 03/04 October 2001, 04/05 October 2001 and 08/09 October 2001, in Figures 1(b) and 1(d)). The initial value of the meridional wind component is set to be v(zi,t0) = vG = 0, while the zonal component follows the function u(zi ≤ 100 m, t=0) = uG-uG(1-zi/100), and for the remaining of the domain u = uG. The initial profile for the wind components was an arbitrary choice, as it was not possible to determine them from the observed data as it was done for temperature and humidity.
while all the other fluxes are assumed to be null at the start of the simulations.The initial conditions for temperature and specific humidity are taken from the first observation of each night, as shown in Figure 1 (solid lines). The initial values of both T(zi,t0) and q(zi,t0), have been obtained through a polynomial interpolation of the real data (dashed lines). For cases whose data do not reach the domain top, the function was just extrapolated up to the top (e.g. nights of 03/04 October 2001, 04/05 October 2001 and 08/09 October 2001, in Figures 1(b) and 1(d)). The initial value of the meridional wind component is set to be v(zi,t0) = vG = 0, while the zonal component follows the function u(zi ≤ 100 m, t=0) = uG-uG(1-zi/100), and for the remaining of the domain u = uG. The initial profile for the wind components was an arbitrary choice, as it was not possible to determine them from the observed data as it was done for temperature and humidity.4. Results and Discussion
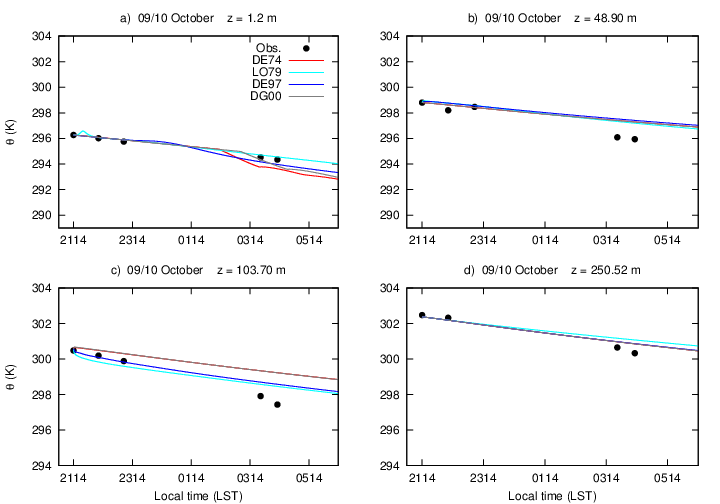
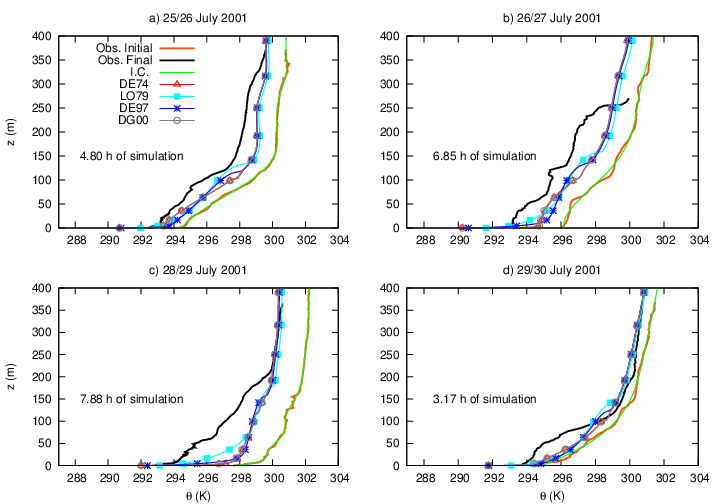
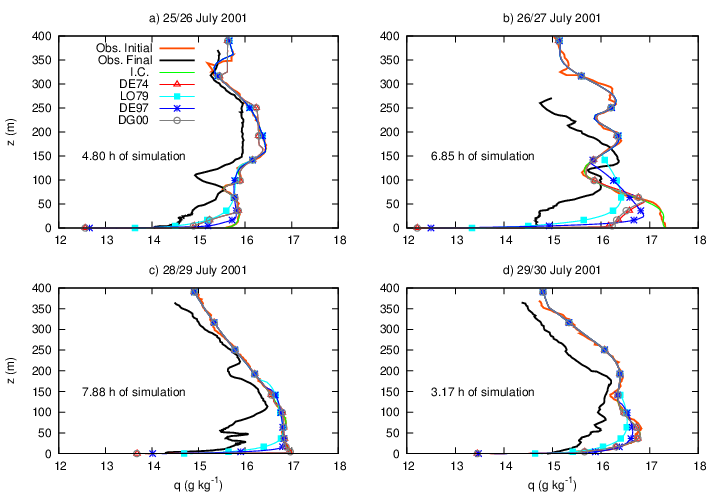
- For the comparison of the stability functions, the model described in the previous section was used to simulate the temporal evolution of temperature and specific humidity profiles along the eight nights described in section 2. Figure 2 shows the temporal evolution of temperature in different atmospheric levels, for all formulations, in a specific night. Near the surface, at 1.2 m, the behaviour using LO79 stability function differs from the others since the start of the simulation (Figure 2(a)). After a slight warming, turbulent mixing increases and causes an almost constant temperature decrease along the night (from 2130 LST). However, the surface energy loss is not enough to provide the observed surface cooling rate. When formulation DE97 is used, results are similar, but the subtle temperature increase is smaller than in the previous case and occurs after 2 hours of simulation time (2314 LST). It is also observed that after such initial increase, a constant temperature decrease happens during the last hours of the simulations. When DE97 is used, the radiative term leads to colder temperatures than when the formulation LO79 is applied. Such a difference can reach almost 0.5 K by the end of the night. When formulations that depend on the Obukhov length are considered (DE74 and DG00), temperature decreases almost uniformly along the simulation, until around 0030 LST, when a rapid temperature drop occurs, first in the DE74 formulation, and then, after a short time, also when the formulation DG00 is used. However, both cases remain slightly warmer than in the DE74 case. The sudden temperature decrease in the middle of the simulations is caused by a wind speed increase (figure not shown). Such intense wind intermittent events have been reported in the real SBL [43, 44] and also in numerical solutions using simple SBL schemes [45]. Besides the distinction between turbulence formulations near the surface, the results at the upper levels are also improved (Figures 2 (b) – 2(d)), so that temperatures in all cases (Figures not shown) are closer to the observations. Such improvement is not caused by the better performance of the turbulence formulations when the vegetation is considered, but, rather, by the better performance of the radiation scheme in this case. This result is supported by previous studies, such as van de Wiel et al. [41] and Steeneveld et al. [9], confirming the important role of the vegetated surface in modelling the SBL.For all nights analysed, the mixing length formulations that depend on Ri lead to warmer temperatures near the surface, as observed in Figure 2(a). It is important to address what causes such differences. When stabilities functions LO79 e DE97 are considered, turbulence intensity is larger than when formulations that depend on the Obukov length are used (figure not shown). As the turbulent mixing increases, the air layer near the surface is warmed by the downward transport of warmer air from the upper part of the SBL. This is confirmed by the fact that in the upper levels there is a temperature decrease larger than when the formulations DE97 e DG00 are used (Figure 2(b) and 2(c)). This is most clearly observed in Figure 2(c), because at 103 m the temperature gradients caused by the surface cooling are smaller than they are at 48 m (Figure 2(b)).The atmospheric level located at 250 m is above the SBL top, and at this height just the radiative flux divergence controls the temperature (Figure 2(d)).The temperature profile evolutions for the four nights of the July campaign are shown in Figure 3. Figure 3(a), shows the performance of the turbulence formulations for the night of 25/26 July of 2001. The main differences happen near the surface, where the temperature solved by the LO79 formulation is more than 1 K warmer than those solved by the others formulations. At a time of 4.8 hours after the first sounding, the general shape of the initial temperature profile still persists, indicating that the temporal evolution of the temperature profile is basically controlled by the radiative loss. The model solutions also provide similar profile shapes, indicating that, despite its simplicity, the radiative scheme reproduces the real SBL behaviour well. Furthermore, one can notice that formulations LO79 and DE97 lead to slightly colder temperatures near the SBL top, a consequence of the stronger turbulent mixing allowed by those formulations. The initial potential temperature profile at the night of 26/27 July (Figure 3(b)) shows a less stable night than shown in Figure 3(a), and after 6.85 hours, temperature at the upper SBL is close to what was observed at that level in the initial profile, indicating a night with small radiative cooling. Model performance in this case is not good, either near the surface or in the upper SBL. The night of 28/29 July was also weakly stable at the time of the first sounding (Figure 3(c)). However, during this night, just after one hour of the first observation the surface temperature falls about 2 K (Figure not showed). This temperature decrease is not assimilated in the simulations, so that the model error increases along the night. Nevertheless, the performance of the radiative scheme is not affected by the surface temperature changes, and the model results above the SBL approach the observed temperature value. The changes observed along this night near the surface could be caused by advection of cold air, which is not prescribed or evaluated by the model. The night of 29/30 July, as the night of 25/26 July, is a night with strong stratification and the difference between the temperature near the surface and the temperature at the SBL top is almost 7 K. As discussed in the first night of this campaign, the model results near the surface and above the SBL top approach considerably to the observation, however, the last sounding of the night, 3.17 hours after the first, the temperature profile shows a cold air layer which last until 50 m, probably caused by occurrence of a local turbulent event which may lead the air just above the cold ground surface to be mixed with the warmer air present at levels above. This hypothesis could be supported by the fact that under very stable conditions, as shown in Figure 3(d), the surface becomes energetically disconnected from the upper levels of the SBL [3, 4], and weak winds tend to cool the intermediate levels of the SBL, as the turbulent mixing is restrained to the lower portion of the boundary layer. This fact is, again, not reproduced by the model. However, in this case, the model results are close to the observations, a result attributed mainly to the good performance of the radiative scheme.Figure 4(a) shows the comparison between the results obtained after 7.2 hours of simulation with the soundings of the night of 03/04 October of 2001. Among all nights studied here, this was the worst result obtained by the model simulations. At the beginning of the night the temperature profile curvature indicates a very strong stratification, which is however, drastically reduced after 7.2 hours. This result shows that the model is not able to reproduce such a change along the night. On the other hand, for the remaining nights of the October campaign, the model estimations for the temperature profile are done satisfactorily. For 04/05 October, the model estimation at the surface is, in all formulations, around 1 K cooler than the surface observation. However, higher in the SBL, the turbulence mixture simulated by the model (clearly observed in LO79 formulation) makes the model temperature profile approach the last temperature sounding of the night (7.15h after the first observation). For 08/09 of October, the simulated temperature profiles are quite close to the observed temperature profile, even after 6.6 hours of the first sounding (Figure 4(c)). It is interesting to notice that the last sounding of the night is shallow and only shows the temperature profile within the SBL. Nevertheless, even in such a lower part of the SBL, model results are appreciably good. In most of the cases previously discussed, good performances were usually attributed to the radiative scheme. However, in this case the good performance is directly related to the model ability to correctly estimate the turbulent mixture. In spite of the night shown in Figure 4(c) being strongly stratified, the stability reduction along the night was reproduced by the model. It is clear that the LO79 formulation reaches the best result among all turbulence formulations used, and this fact shows how important it is, under very stable conditions, to maintain some turbulent activity even when the theory predicts that none should exist. The last night of October campaign (09/10 October) is presented in Figure 4(d). As in the other nights of October, the initial sounding (2114 LST) is strongly stratified. However, along the night, temperature drops more within the SBL than it does above it. The increased at lower levels is better reproduced by the formulations that use the Richardson number as a stability parameter. Again, this is a consequence of these schemes (LO79 and DE97) preserving turbulent mixing even in the most stable conditions. This inference is supported by the fact that in the most stable nights, with a sharper temperature profile, the best performance was achieved using LO79 formulation, which is the one that provides the most mixing in very stable situations. Specific humidity profiles from both campaigns also support this conclusion (Figures 6 and 7).The model performance for specific humidity for the July campaign is presented in Figure 5. For the night of 25/26 July one can observe that after 4.8 hours of simulation the model has deviated from the initial profile only at the lowest 150 m, near the surface. The largest distinction from the initial condition, in this case, is observed for the formulations that depend on the Richardson number. At the surface, all formulations underestimate the specific humidity, and it is a consequence of the low temperatures estimated While at the surface DE74 and DG00 provided the driest values, they only deviate from the initial conditions for 30 m above the surface. At the upper atmosphere, the value of the first and last sounding are quite similar to each other. Something similar happens for all formulations at the night of 26/27 July (Figure 5(b)). The first sounding of this night shows high values of specific humidity in the first 60 m above the surface, indicating fog. Along the night, specific humidity near the surface decreases, following temperature, as the air is saturated. The changes that occurred in the observed values of both temperature and moisture probably were caused by advection, and this fact may explain the inability of the model in forecast both quantities along the night. This result has some similarities with those obtained for the night of 28/29 July (Figure 5(c)). The first sounding of the night, as in the previous case, also shows fog (2130 LST), and moisture evolution along the night follows closely temperature variation along the night (Figure 3(c)). After the first hours, specific humidity decreases so that by the time of the last sounding (0523 LST), the specific humidity near the surface surface is almost 3 g kg-1 drier than it was at the first observation. At the surface, the specific humidity is well predicted by all formulations. However, at upper levels, the model prediction is not good for the specific humidity. The performance for the night of 29/30 July is shown in Figure 5(d). At the time of the first sounding (0125 LST), as discussed when figure 3(d) was shown, there was a strong stratification near the surface. This stratification causes a sharp profile of specific humidity near the surface. However, along the night as the temperature decrease near the surface, specific humidity decreases in the middle portion of the SBL. As discussed before, it could be caused by a local turbulent event originated at the surface. This kind of event, that causes temperature decrease in upper atmospheric levels, also dries the atmosphere as the dry air is carried out to the upper boundary layer from the surface. As happened for temperature, no formulations were able to reproduce such a behavior, mainly due to the reduced turbulence mixing existent in such stable condition.
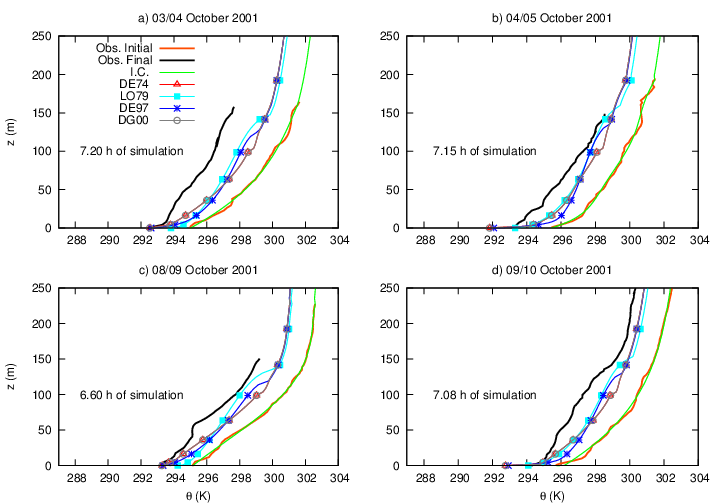 | Figure 4. Same as Figure 3, but, for October campaign |
 | Figure 5. Same as Figure 4, but, for specific humidity |
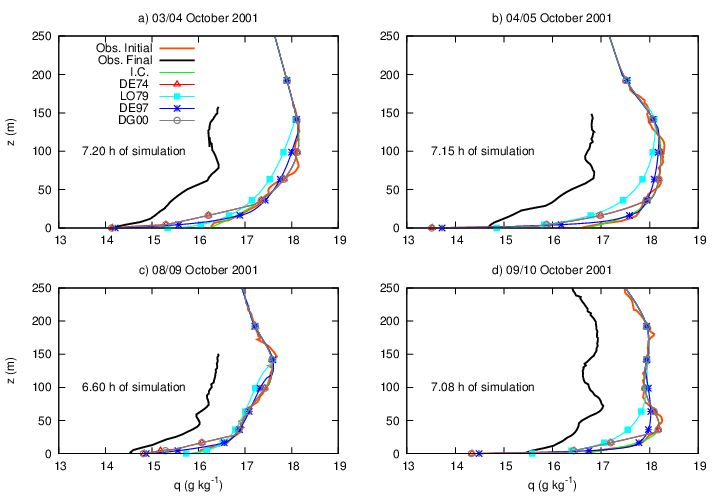 | Figure 6. Same as Figure 5, but, for specific humidity |
5. Conclusions
- The comparison between model results and observed data presently being presents represents a theoretical exercise, where very important aspects, such as an advection scheme, have not taken been considered.. However, some important considerations may be inferred from the results shown.Near the surface, all parameterizations predicted quite well the temperature evolution along the night. This result shows that the simplified surface scheme was able to reproduce correctly the energy exchange in the surface layer. For upper levels, within the SBL, the most turbulent mixing length formulations lead to solutions similar to the observations. In fact, in those cases turbulence transports the cold air from near the surface to the higher levels in the SBL, cooling them. Besides leading to colder results near the surface, formulations that suppress turbulence activity in very stable conditions are not able to couple the surface to the upper SBL [3, 4].Two other interesting aspects of the results must be highlighted, regarding contributions from advection and radiative flux divergence in the atmosphere. In most cases it has been observed that advection must be considered when predicting profile evolution along the night, especially for humidity profiles. At the nights of 28/29 and 29/30 of July, temperature is overestimated by the model within the boundary layer, while above the SBL all formulation predictions agree with the observed profiles. It shows that, however simplified, the radiative scheme was able to reproduce the radiative cooling above the boundary layer. On the hand, humidity predictions depend solely on the turbulent scheme, and results show that in very stable conditions, such as those analysed here, a more complex scheme for humidity, which includes advection, is needed.Finally, it is well known that it is very hard for a numerical model to reproduce the behavior of the mean variables that control the SBL flow, and that it gets harder when one tries to quantitatively reproduce observations in very stable conditions. In this way, and in agreement with previous studies [5, 12], the comparison of different mixing length formulations shows that even in the very stable case, when the Richardson exceeds its critical value, some turbulence activity must be preserved. This happens because in this situation, intermittent turbulence events are often observed, being responsible for almost all the turbulent transport [47]. Once the scheme is not able to reproduce such feature, it is necessary to always maintain some turbulent activity.The good results with the surface and radiation schemes used here motivate to further improve the model by including an advection scheme, and by using more complete scheme for humidity. This is a task for a future work.
ACKNOWLEDGMENTS
- The authors would like to thank the Brazilian agencies CAPES (Coordenação de Pessoal de Nível Superior) and CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) for the financial support.
List of Symbols

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML