-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2015; 5(1A): 15-26
doi:10.5923/s.ajee.201501.03
Dependence of Turbulence-Related Quantities on the Mechanical Forcing for Wind Tunnel Stratified Flow
Giuliano Demarco 1, Franciano Puhales 1, Otávio Costa Acevedo 1, Felipe Denardin Costa 2, Ana Cristina Avelar 3, Gilberto Fisch 3
1Departamento de Física, Programa de Pós-Graduação em Física, Universidade Federal de Santa Maria, Santa Maria-RS, Brasil
2Departamento de engenharia, Universidade Federal do Pampa, Alegrete, Brasil
3Instituto de Aeronautica e espaço, Departamento de Ciência e Tecnologia Aeroespacial, São José dos Campos -SP, Brasil
Correspondence to: Giuliano Demarco , Departamento de Física, Programa de Pós-Graduação em Física, Universidade Federal de Santa Maria, Santa Maria-RS, Brasil.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Wind tunnel experiments of thermally stratified flows are analyzed with the objective of determining the influence of the thermal stratification on turbulence-related quantities. The experimental apparatus consisted of an aluminum plate inserted at the bottom surface of the wind tunnel test section. In order to create a thermally stratified layer, the plate was cooled down to 5ºC and the air entering the tunnel was kept at approximately 20ºC. As the wind speed increases, such stable layer was soon destroyed. Data shows that quantities such as temperature, variances, dissipation rates and turbulent fluxes are substantially reduced when surface cooling is present and that such a reduction is enhanced for weak wind conditions, as these are cases that preserve the stratification. On the other hand, third and fourth order statistical moments, as well as the mean wind speed are much less affected by the stratification.
Keywords: Turbulence, Wind tunnel, Thermal stratification
Cite this paper: Giuliano Demarco , Franciano Puhales , Otávio Costa Acevedo , Felipe Denardin Costa , Ana Cristina Avelar , Gilberto Fisch , Dependence of Turbulence-Related Quantities on the Mechanical Forcing for Wind Tunnel Stratified Flow, American Journal of Environmental Engineering, Vol. 5 No. 1A, 2015, pp. 15-26. doi: 10.5923/s.ajee.201501.03.
Article Outline
1. Introduction
- The study of flows over surfaces with temperature variability, or simply over surfaces whose temperature differs from the ambient temperature, has served as a challenge for scientists for many years. In this work, a special case of this type of flow is studied: stratified flow over surfaces with spatially uniform temperatures.In this type of flow, the fluid is heated or cooled from below, possibly forming a stratified boundary layer, whose characteristics depend on stability. This type of situation occurs, for example, near the Earth surface in the atmospheric boundary layer. In this case, surface heating from the incident solar energy occurs during the day while surface cooling happens at night due to the emission of infra-red radiation.The study of this type of flow has proven over the years to be very complex, especially due to the coupling of mechanical, thermal and transport phenomena to which it is subjected. Furthermore, this task requires a simultaneous understanding of the exchange processes of momentum, heat and sometimes moisture. Here, a stratified and turbulent flow, i.e. subjected to high Reynolds numbers, is discussed. Many efforts have been made to understand this phenomenon, some depicting the conditions of similarity to which it can be associated (Kitaigorodskii, 1988), others seeking numerical solutions for the system of equations (Deardorff, 1972). Because of the inherent complexity of the numerical treatment of the Navier-Stokes and energy equations, and of the limitations of similarity theory for a complete study of this type of flow, the experimental simulation of atmospheric boundary layers in wind tunnels have been used to aid the understanding of this phenomenon.In micrometeorology, the characterization of the atmospheric flow in conditions of stable stratification can be appointed as the most important current scientific problem. This happens because, in the night period when the surface radiative cooling is responsible for the formation of a stable layer, the turbulent intensities are drastically reduced compared to their corresponding values observed in the daytime. Two distinct types of stable boundary layer are observed (Mahrt, 1999). The first, typically referred to as weakly stable layer, occurs when the destruction of turbulence by thermal stratification is small in relation to the production of turbulence associated with vertical wind shear. In this case, although its intensity is reduced, the turbulence is temporally and spatially continuous. In the vertical, continuous turbulence is able to keep the surface connected by turbulence to the top of the layer. As a consequence, the atmosphere above the stable boundary layer (SBL) stays connected to the surface. A second type of SBL occurs when the destruction of turbulence, associated with the thermal stratification, is comparable to the mechanical production. In this case, the SBL is classified as very stable, and turbulence can be almost completely suppressed locally. Thus, there is no connection between horizontally separated locations and the air at lower levels is no longer coupled to the higher levels of the atmosphere. This way, the layers above the SBL do not exert influence in the variables observed at the surface. The very stable boundary layer is, in particular, the greatest current challenge for atmospheric boundary layer researchers, which not yet well understand various aspects related to it. Among these are the controls on the coupling state; the forcing for intermittent turbulent events, and their characteristics; the role of non-turbulent flows and how the various phenomena that occur simultaneously in the period, interact spatially and temporally. The SBL has been widely studied in recent years. Field observations are still the main tool for this purpose (Poulos et al., 2002; Sun et al., 2002; Acevedo et al. 2003; Banta et al, 2007; Acevedo et al., 2014; and others), but modeling studies (Duynkerke, 1988; Beare et al., 2006; Cuxart et al., 2006; Costa et al, 2011; and others) are also performed. These, however, are typically restricted to conditions of weakly stable layer, because the numerical schemes still have difficulty in reinstate the turbulent mixture once it is fully suppressed. Observations in wind tunnels have been used to study the turbulent flow in conditions of stable thermal stratification (Lienhard et al., 1990;. Yoon et al, 1990; Ohya et al., 1997; Ohya, 2001; Ohya et al, 2008). In these studies, vertical profiles of turbulent statistical moments are presented and it is analysed how they are affected by the thermal stratification. The aim of the present paper is to describe an initiative to study turbulent flow on a stable surface in a wind tunnel. Focus is given to the effect of the thermal stratification on different statistical moments of the turbulent field.
2. Experimental Setup
- Experiments were performed in a wind tunnel at Instituto de Aeronáutica e Espaço (IAE/DCTA), São José dos Campos, Brazil. The wind tunnel is of a recirculation type having a rectangular test section, 1200 mm long, 720 mm wide, 500 mm high. Designed to produce thermally stratified flows, the test section was equipped with a cooling system. Such an apparatus consisted of an aluminum plate inserted at the bottom surface of the wind tunnel test section. In order to create a thermally stratified layer, the plate was cooled down to 5 °C, while the air entering the tunnel was kept at approximately 20 °C.The experimental arrangement for stable boundary layer simulation is shown in figure 1. The boundary layer was artificially tripped by a 40-mm high fence at the entrance to the test section. The flow condition upstream of the fence is uniform with less than 2 % turbulence intensity. A stably stratified flow is created by cooling the test-section floor at around 5 °C, as shown in Figure 1. Stratified turbulent boundary layers with free stream velocities U from 1 to 5 m.s-¹, varying at 0.5 m.s-¹ steps have been created, covering a range of stabilities from weakly stable to neutral.
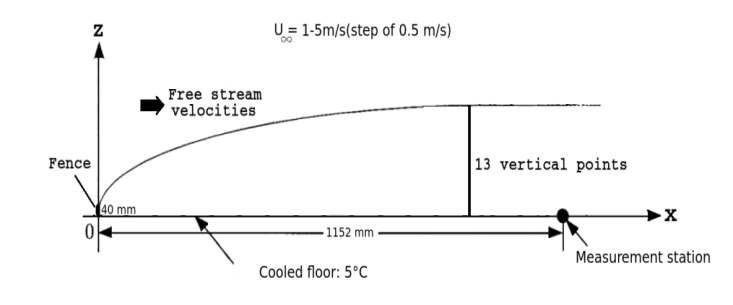 | Figure 1. Experimental Arrangement. (Adapted Ohya(2001)) |
|
3. Results and Discussion
3.1. Profiles Obtained from Hot-Wire Data
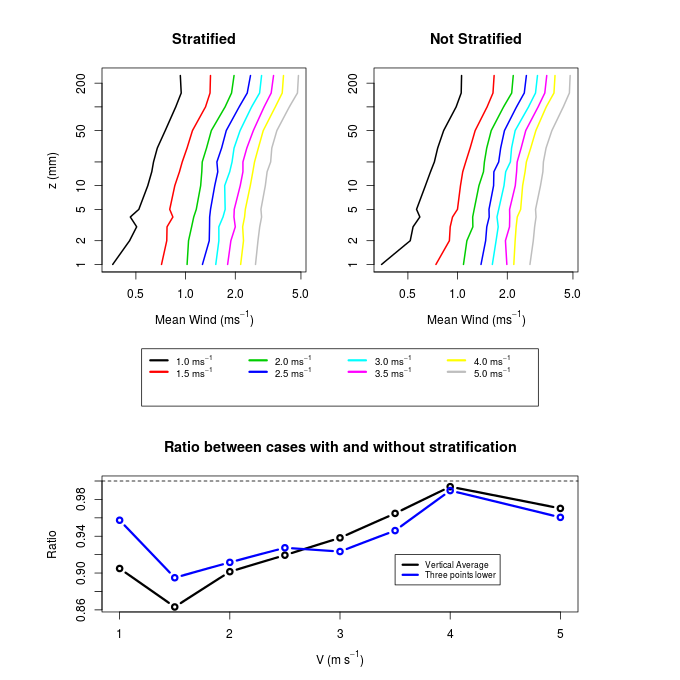
- In this subsection, we present the profiles of quantities derived from observations made with hot wire anemometry. These are variables that depend only on the longitudinal wind fluctuations, in addition to observations of temperature.The temperature profiles show the thermal stratification destruction provided by the turbulent mixing (Fig. 2). It is remarkable that the stability is much more intense in cases with low wind, decreasing progressively with increasing the mechanical forcing. Similar results have been obtained in simulations of wind tunnel (Ohya, 2001), but in that case the contrast was not so great because wind speeds were relatively more similar to each other than the values presented in Figure 2.
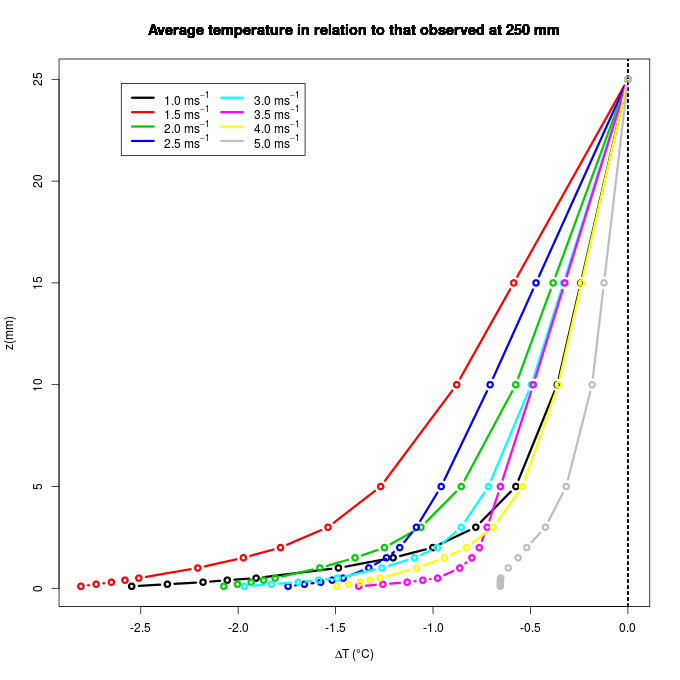 | Figure 2. Mean temperature profiles as a function of wind speed as given by legend. In each case, the profiles were considered in relation to the temperature value at the highest level sampled |
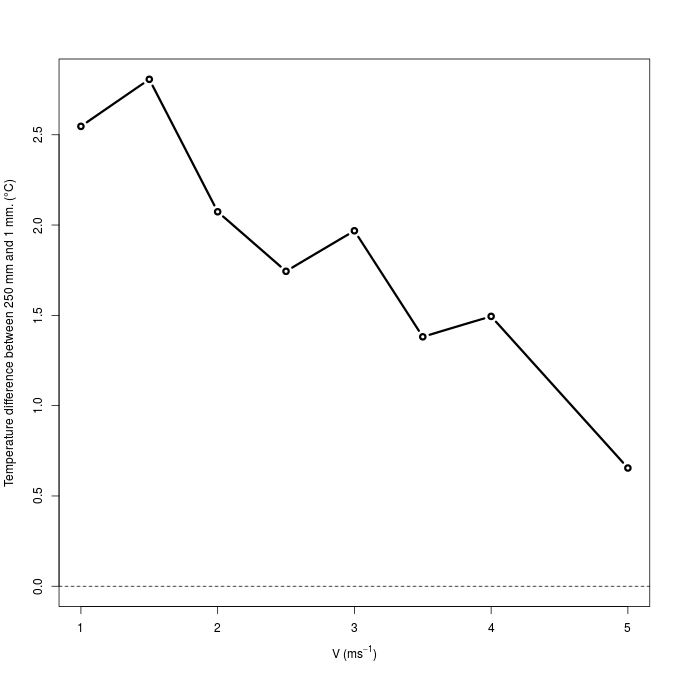 | Figure 3. Temperature difference between the lowest and the highest level sampled a function of mean wind |
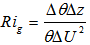 | (1) |
|
 The greatest influence of the thermal stability is in the velocity fluctuations, as can be expected by the turbulent kinetic energy (TKE) budget equation, which determines that under stable conditions, there is turbulence destruction associated with the vertical temperature gradient.Thus, it is expected that in low wind cases, when the vertical temperature gradient is greater (as shown in Fig. 2), there should be a notable reduction of turbulent fluctuations. This is, indeed, observed in Fig. 5. The variance of the turbulent fluctuations is approximately constant up to 100 mm, a layer that coincides with the logarithmic vertical profile of the mean wind. Ohya (2001) observed that in most cases of static stability the magnitude of the velocity fluctuations showed a peak near the surface. Such a peak was not observed in this study for any stability case. In contrast, in all cases, the turbulent velocity fluctuations were nearly constant in magnitude for an entire layer from the surface to 100 mm. The greatest reduction of velocity fluctuations from the case with no stratification to the stratified case occurred the case at the 1.5 m.s-1 experiment when it reached 40% (Fig. 4, bottom panel). In general, cases with less wind (and consequently increased thermal stratification) had the largest reductions of the wind variance by the thermal stratification. When the wind reaches 4 to 5 m.s-1, this reduction did not reach 10%.
The greatest influence of the thermal stability is in the velocity fluctuations, as can be expected by the turbulent kinetic energy (TKE) budget equation, which determines that under stable conditions, there is turbulence destruction associated with the vertical temperature gradient.Thus, it is expected that in low wind cases, when the vertical temperature gradient is greater (as shown in Fig. 2), there should be a notable reduction of turbulent fluctuations. This is, indeed, observed in Fig. 5. The variance of the turbulent fluctuations is approximately constant up to 100 mm, a layer that coincides with the logarithmic vertical profile of the mean wind. Ohya (2001) observed that in most cases of static stability the magnitude of the velocity fluctuations showed a peak near the surface. Such a peak was not observed in this study for any stability case. In contrast, in all cases, the turbulent velocity fluctuations were nearly constant in magnitude for an entire layer from the surface to 100 mm. The greatest reduction of velocity fluctuations from the case with no stratification to the stratified case occurred the case at the 1.5 m.s-1 experiment when it reached 40% (Fig. 4, bottom panel). In general, cases with less wind (and consequently increased thermal stratification) had the largest reductions of the wind variance by the thermal stratification. When the wind reaches 4 to 5 m.s-1, this reduction did not reach 10%.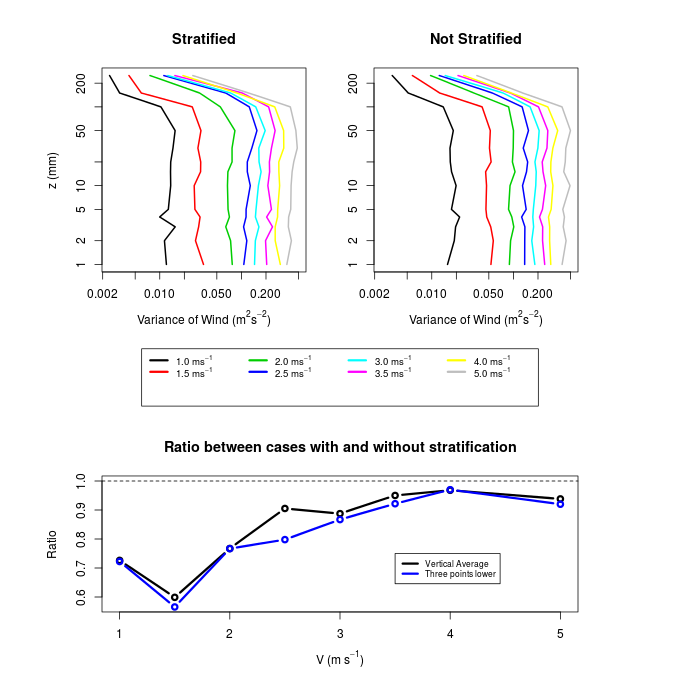 | Figure 5. Same as in figure 4, but for the variance of the longitudinal wind fluctuations |
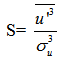 | (2) |
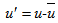 are the turbulent fluctuations of longitudinal velocity,
are the turbulent fluctuations of longitudinal velocity, 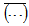 is the average operator and σu is the standard deviation of u. This coefficient indicates whether there is a more common direction of the velocity fluctuations around the average, being zero for a perfectly symmetrical distribution. Equivalently, the kurtosis is defined as
is the average operator and σu is the standard deviation of u. This coefficient indicates whether there is a more common direction of the velocity fluctuations around the average, being zero for a perfectly symmetrical distribution. Equivalently, the kurtosis is defined as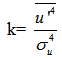 | (3) |
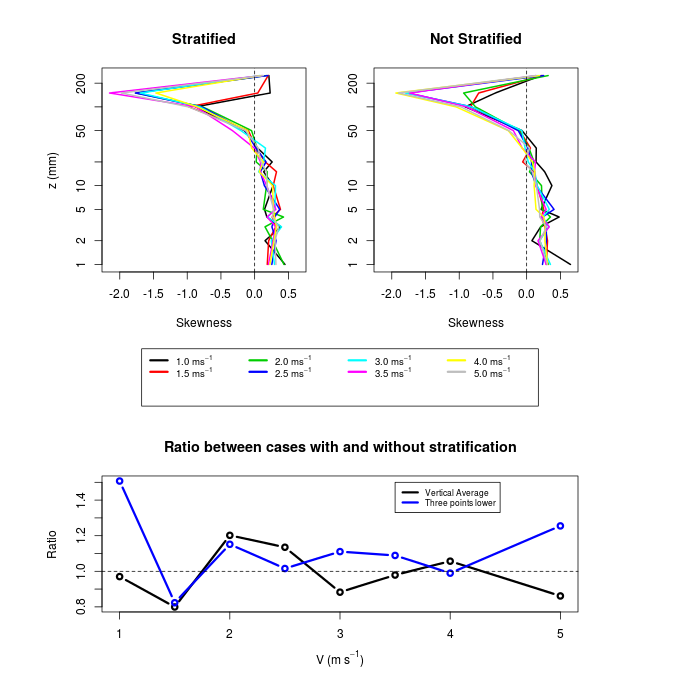 | Figure 6. Same as in figure 4, but for the skewness coefficient. In the upper panels, dotted line represents zero |
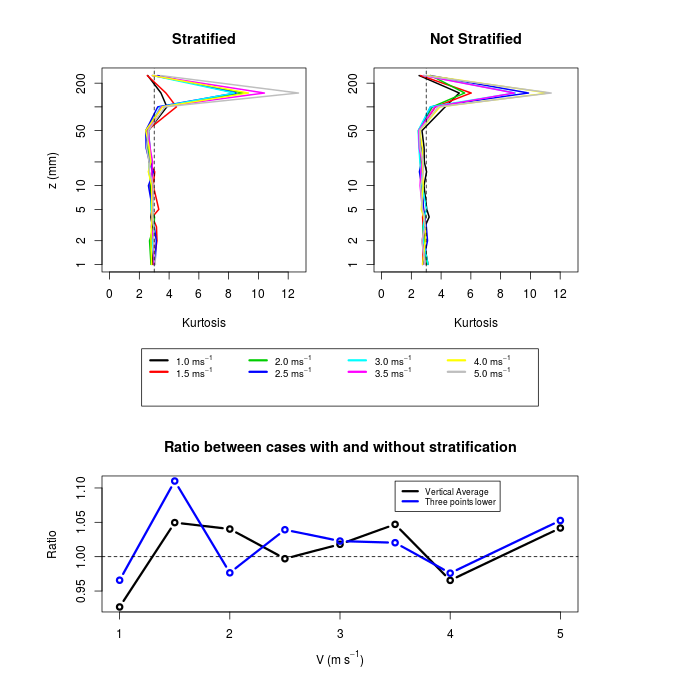 | Figure 7. Same as in figure 4, but for the kurtosis coefficient. In the upper panel, the dotted line indicates the value 3, typical of a Gaussian distribution |
3.2. Profiles Obtained Data PIV
- Vertical velocity fluctuations data are only available through particle images velocimetry (PIV). These are needed for determining some relevant quantities in a stable boundary layer, such as vertical turbulent fluxes and vertical eddy diffusion coefficients. It is important to note that, in general, the data presented here show more scatter than in the previous section, and this is mainly due to the different observation technique used. The vertical profiles of the turbulent flux
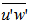 show a maximum in both stratified and not stratified cases at heights between 50 and 100 mm for all wind speeds (Fig. 8). Similar profiles have been observed in previous studies that reported experiments of wind tunnel with flow over vegetated areas (Brunet; Finnigan; Raupach, 1994; Zhu et al., 2006; Zhu; Hout; Katz, 2007). In these studies, the peak of momentum flux coincides with the height of the roughness elements used. This suggests, therefore, that the maximum observed here is associated with the fence of 40 mm used to maintain a boundary layer with well-developed turbulence in the simulations. The momentum flux is affected by stratification, and this influence is greater in levels near the surface. This is shown in the bottom panel of Figure 8, which shows that the first 10 levels of PIV observation, when the wind is 1 m.s-1, the magnitude of
show a maximum in both stratified and not stratified cases at heights between 50 and 100 mm for all wind speeds (Fig. 8). Similar profiles have been observed in previous studies that reported experiments of wind tunnel with flow over vegetated areas (Brunet; Finnigan; Raupach, 1994; Zhu et al., 2006; Zhu; Hout; Katz, 2007). In these studies, the peak of momentum flux coincides with the height of the roughness elements used. This suggests, therefore, that the maximum observed here is associated with the fence of 40 mm used to maintain a boundary layer with well-developed turbulence in the simulations. The momentum flux is affected by stratification, and this influence is greater in levels near the surface. This is shown in the bottom panel of Figure 8, which shows that the first 10 levels of PIV observation, when the wind is 1 m.s-1, the magnitude of 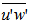 in the stratified case corresponds to only 40% of the value of no stratified case. In the vertical average, the reduction is smaller, but still substantial, where the value of the stratified case corresponding to 75% of that observed in the condition without stratification. The difference between the two cases is reduced with winds of 2 m.s-1 and becomes almost non-existent for winds of 3 m.s-1 or more intense.It is also possible to determine from the data of PIV the turbulent vertical flux of turbulent kinetic energy (TKE) (Fig. 9), defined as half of the sum of the variances of the three wind components. In this case, it is important to emphasize that this is not the TKE itself, but the contributions of the variances of the u and w components, available in the measurements of PIV. Thus, the flux is the amount
in the stratified case corresponds to only 40% of the value of no stratified case. In the vertical average, the reduction is smaller, but still substantial, where the value of the stratified case corresponding to 75% of that observed in the condition without stratification. The difference between the two cases is reduced with winds of 2 m.s-1 and becomes almost non-existent for winds of 3 m.s-1 or more intense.It is also possible to determine from the data of PIV the turbulent vertical flux of turbulent kinetic energy (TKE) (Fig. 9), defined as half of the sum of the variances of the three wind components. In this case, it is important to emphasize that this is not the TKE itself, but the contributions of the variances of the u and w components, available in the measurements of PIV. Thus, the flux is the amount 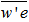 , where
, where 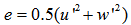 Of all the variables presented here, this presents the greatest statistical uncertainty, because it is a third moment obtained from the PIV data. Anyway, a significant pattern is noticeable, with negative fluxes in the lower levels and positive values aloft. The large fluctuations observed do not allow any conclusions with respect to differences between stratified and not stratified cases. Finally, PIV data also allow to obtain the eddy diffusivity coefficients of momentum (Fig. 10). This is defined as the coefficient of proportionality between the turbulent fluxes of momentum and the vertical gradients of velocity, being therefore determined as
Of all the variables presented here, this presents the greatest statistical uncertainty, because it is a third moment obtained from the PIV data. Anyway, a significant pattern is noticeable, with negative fluxes in the lower levels and positive values aloft. The large fluctuations observed do not allow any conclusions with respect to differences between stratified and not stratified cases. Finally, PIV data also allow to obtain the eddy diffusivity coefficients of momentum (Fig. 10). This is defined as the coefficient of proportionality between the turbulent fluxes of momentum and the vertical gradients of velocity, being therefore determined as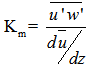 | (4) |
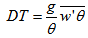 | (5) |
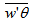 is the vertical turbulent sensible heat flux, and it is impossible to be determined due to the absence of measurements of the fluctuations of temperature and vertical velocity in the same system of measurement. On the other hand, it is possible to make a qualitative estimation of this term, estimated by the traditional theory K, which relates fluxes to the vertical gradients through the turbulent diffusivities by the expression
is the vertical turbulent sensible heat flux, and it is impossible to be determined due to the absence of measurements of the fluctuations of temperature and vertical velocity in the same system of measurement. On the other hand, it is possible to make a qualitative estimation of this term, estimated by the traditional theory K, which relates fluxes to the vertical gradients through the turbulent diffusivities by the expression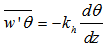 | (6) |
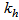 is the turbulent diffusivity of sensible heat and
is the turbulent diffusivity of sensible heat and 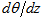 is the vertical temperature gradient, shown in Figure 2. Ohya (2001) shows that for values Richardson number smaller 0.1 the relationship between turbulent diffusivity of sensible heat and momentum is approximately constant and equal to Kh/Km = 0.8. Thus, one can use the eddy diffusivity coefficients of momentum shown in Figure 10, together with the vertical temperature profiles (Figure 2) for estimating the term thermal destruction of turbulence. It is also important to normalize the data to obtain an estimate of the importance of this term in relation to other terms of the balance equation of TKE.To normalize the thermal destruction term was chosen the dissipation term, which is obtained from the structure function, and represents an independent measure of the PIV observations. The results are shown in Figure 11 and confirm the most important role of thermal destruction in the case of weak wind, when the thermal stratification is more intense. The destruction of turbulence by thermal stratification reaches a maximum between the height of 1 and 10 mm, where there is sufficient turbulent diffusivity, with a temperature gradient still appreciable. With wind 1 m.s-1, the estimated thermal destruction reaches 0.8% of the average dissipation, while in high wind conditions this value does not reach 0.1%. Anyway, it is important to note that in all cases the thermal destruction estimated in this way is smaller than the dissipation rates, while the observed reduction of the variances of speed when the wind is weak indicates that the thermal destruction must have rather a relevant role. We attribute this discrepancy partially to the uncertainty associated with the use of different observational techniques, and therefore cannot show a reliable closing balance of TKE. Nevertheless, it is important to notice that atmospheric boundary layer studies in weakly stable conditions have shown the buoyant destruction to be at least one order of magnitude smaller than the dissipation rate (kosovic; Curry, 2000; Shah; Bou-Zeid, 2014).
is the vertical temperature gradient, shown in Figure 2. Ohya (2001) shows that for values Richardson number smaller 0.1 the relationship between turbulent diffusivity of sensible heat and momentum is approximately constant and equal to Kh/Km = 0.8. Thus, one can use the eddy diffusivity coefficients of momentum shown in Figure 10, together with the vertical temperature profiles (Figure 2) for estimating the term thermal destruction of turbulence. It is also important to normalize the data to obtain an estimate of the importance of this term in relation to other terms of the balance equation of TKE.To normalize the thermal destruction term was chosen the dissipation term, which is obtained from the structure function, and represents an independent measure of the PIV observations. The results are shown in Figure 11 and confirm the most important role of thermal destruction in the case of weak wind, when the thermal stratification is more intense. The destruction of turbulence by thermal stratification reaches a maximum between the height of 1 and 10 mm, where there is sufficient turbulent diffusivity, with a temperature gradient still appreciable. With wind 1 m.s-1, the estimated thermal destruction reaches 0.8% of the average dissipation, while in high wind conditions this value does not reach 0.1%. Anyway, it is important to note that in all cases the thermal destruction estimated in this way is smaller than the dissipation rates, while the observed reduction of the variances of speed when the wind is weak indicates that the thermal destruction must have rather a relevant role. We attribute this discrepancy partially to the uncertainty associated with the use of different observational techniques, and therefore cannot show a reliable closing balance of TKE. Nevertheless, it is important to notice that atmospheric boundary layer studies in weakly stable conditions have shown the buoyant destruction to be at least one order of magnitude smaller than the dissipation rate (kosovic; Curry, 2000; Shah; Bou-Zeid, 2014).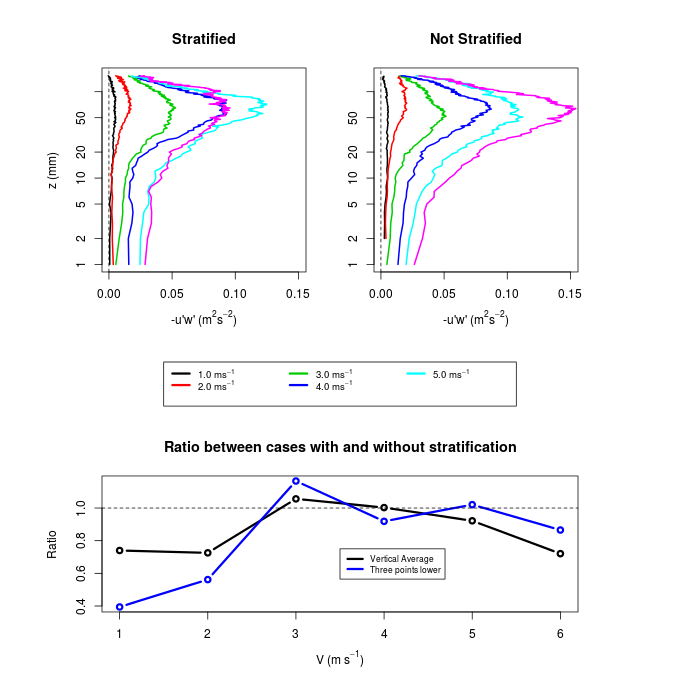 | Figure 8. Same as in figure 4, but for the absolute values of turbulent momentum fluxes |
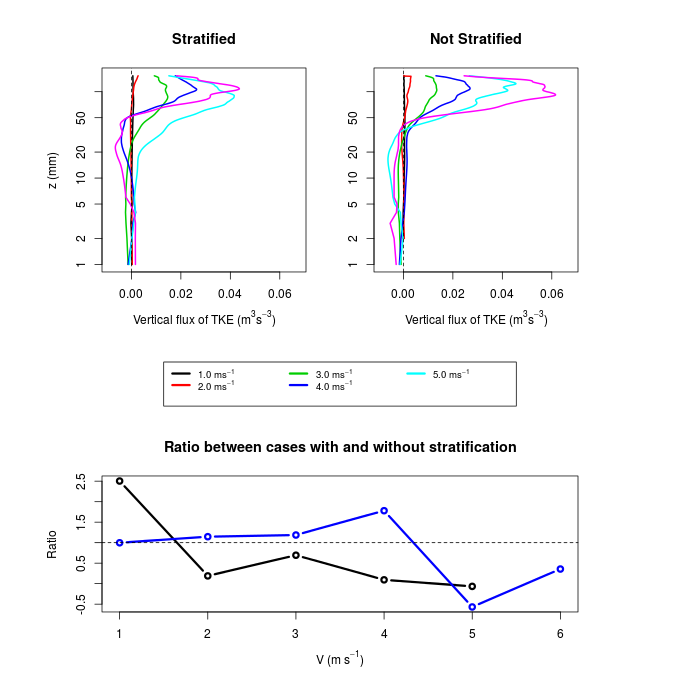 | Figure 9. Same as in figure 4, but for turbulent vertical flux TKE |
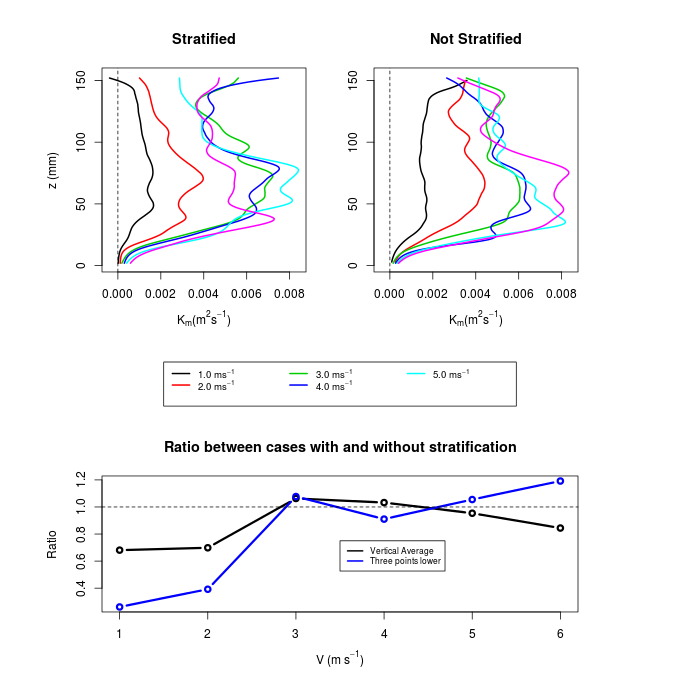 | Figure 10. Same as in figure 4, but for the eddy diffusivity coefficients of momentum |
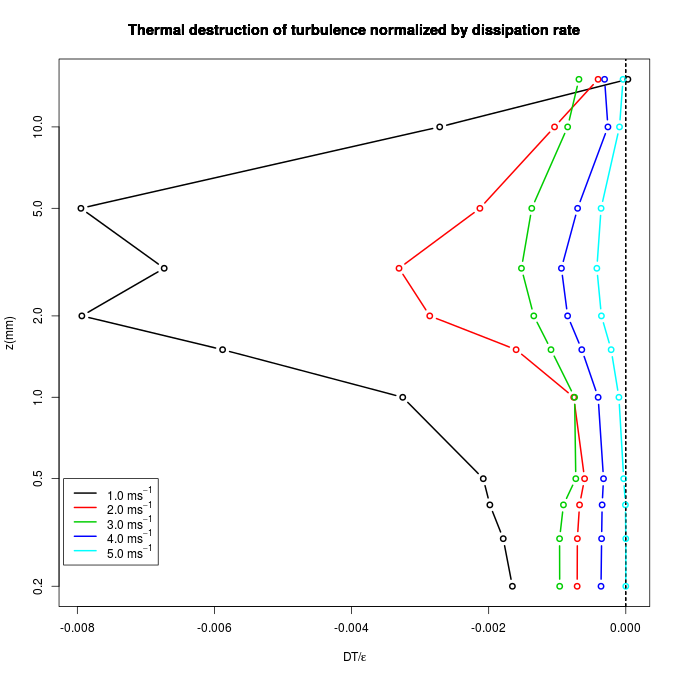 | Figure 11. Thermal destruction Term, estimated as described in the text for different values of wind velocity. In each case, the profiles were normalized by the vertical average rate dissipation |
4. Conclusions
- The experiments performed in a wind tunnel over a cooled surface presented in this paper allowed us to obtain some interesting results. Among these are:- A stratified layer is formed, however, quickly destroyed by winds of moderate intensity. Even in the case of weak wind of 1 m.s-1, the stratified layer that was formed could not be characterized as a very stable boundary layer having Richardson number below 0.1;- Even not being a very stable stratification, other quantities associated with turbulent flow, in addition to the temperature profile showed substantial reduction in cases of weaker wind. Among these, we highlight the variances of the turbulent velocity fluctuations, the dissipation rate, the vertical turbulent fluxes of momentum and eddy diffusivity coefficients;- Other quantities were not significantly affected by thermal stratification. Among these, the most relevant is the average wind profile. Statistical moments of third (skewness) and fourth order (kurtosis) also had no relevant changes between stratified and not stratified cases.
ACKNOWLEDGEMENTS
- The authors are gratefully indebted to Capes (Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior, Brasil), CNPq (Conselho Nacional de Desenvolvimento Cientíico e Tecnológico, Brasil) for the financial support of this work and DCTA (Departamento de Ciência e Tecnologia Aeroespacial) for the technical support.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML