Fareha Asim1, Muzzaffar Mahmood2
1Department of Textile Engineering, NED University of Engineering & Technology Karachi, Pakistan
2Department of Mechanical Engineering, NED University of Engineering & Technology Karachi, Pakistan
Correspondence to: Fareha Asim, Department of Textile Engineering, NED University of Engineering & Technology Karachi, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The study was carried out to develop the mathematical model of crease recovery angle for single step fixation process of cotton fabric for reactive printing and crease resistance finishing using design of experiment.Single step fixation process using Monochlorotriazine (MCT) based reactive dye and modified dimethyloldihydroxy ethylene urea (DMDHEU) based crease resistantwas investigated to model the relationship of significant factors on the dry crease recovery angle. The effects of several factors governing the single step process, such as dye concentration, concentration of crease resistant, fixation method and temperature, on dry crease recovery angle were examined.Initially sets of screening experiments have been conducted to identify the significant factors and their interaction.Furthermore, the detailed analysis of significant factors including ANOVA, residual analysis, model adequacy checking and regression analysis has been performed.However, mathematical model have been developed as a function ofsignificant factors namely concentration of crease resistant, fixation method and fixation temperature. The statistical analysis of the significant factors revealed the quadratic effect of each factor on the crease recovery anglein single step fixation process. The uncertainty analyses for measurements shows that the predicted values are in good agreement with experimental data and are sufficiently accurate.
Keywords:
Crease Resistance Finishing, Design of Experiment, Dry Crease Recovery Angle, Mathematical Modelling, Reactive Printing
Cite this paper: Fareha Asim, Muzzaffar Mahmood, Mathematical Modelling of Dry Crease Recover Angle for Single Step Fixation of Reactive Printing and Crease Resistance Finishing of Cotton Fabric Using DOE, International Journal of Textile Science, Vol. 2 No. 3, 2013, pp. 59-71. doi: 10.5923/j.textile.20130203.03.
1. Introduction
In Textile processes, it is often of primary interest to develop the relationships between the key process variables and the performance characteristics. MathematicalModelling play an important role in developing, analysing and predictingthe relationship from experiments with certain level of confidence[1-6].When several variables influence a certain characteristic of a product, the best strategy is then to design an experiment(DOE) so that objective conclusions can be drawn rather than judgemental. In the context of DOE in Textiletwo types of process variables: qualitative and quantitative factors[7-12]. The aim of this work was to develop the mathematical model of crease recovery angle for single step fixation process of reactive printing and crease resistance finishing process.The significant factors for the single step fixation of reactive printing and crease resistance finishing process had been reviewed previously [13-16].In the current studyof single step fixation process of reactive printing and crease resistance finishing chroma, concentration of crease resistant and fixation temperature are quantitative factors. However fixation method is the qualitative factor.
2. Experimental
2.1. Process Route
The singlestep fixation of reactive printing and crease resistance finishing is carried outas follows: Crease Resistant Finish-Dry-Reactive Print-Fix-Wash-Dry-Conditioned.In the first step ready to print fabric was padded with thecrease resistant finish liquor, and then squeezed to obtain a 70% wet pickup. The fabric was then dried at 100°C for 1 min. The dried fabric was printed by lab scale Rotary Printing machine. The finish-print fabric was concurrently fixed using Econtrol method at 135°C for 5 minutes. The fixed samples were finally washed, dried and conditioned.
2.2. Evaluation of Dry Crease Recovery Angle (DCRA)
The crease resistant properties were evaluated by measuring the dry crease recovery angles (DCRA). The print-finish fabrics were conditioned (at temperature 25±1oC and relative humidity 65 ±1%) before the measurement of DCRA values. The dry crease recovery angle (DCRA) of the fabric was measured using AATCC test method 66-1990. The wider the DCRA is, the higher the crease recovery. The samples processed with single step fixation were compared with those produced from a conventional two-step process of reactive printing and Crease resistance finishing.The experiment data is shown in Table 1 and 2.
2.3. Statistical Analysis of the Data
After processing the experimental trials, DCRAvalues were measured using crease recovery tester.The results obtained from the different experimental sets are presented in Table 2. The DCR Avalues were statistically analysed. Residual analysis and model adequacy checking were performed. The experiments have been conducted in random order. The results were analysed using software Design Expert 8.0.
2.4. Model Adequacy Checking
2.4.1. The Normality Assumption
The normal probability plot of the residual for dry crease recovery angles has been shown in Figure 1. There is no severe indication of non-normality, nor is there any evidence pointing to possible outliers and the equality of variance assumption does not seem to be violated. 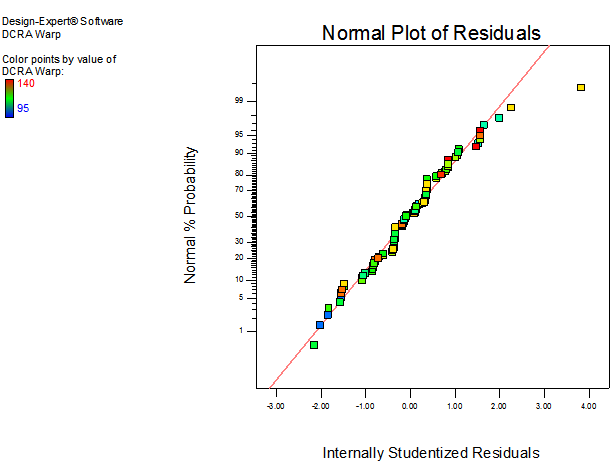 | Figure 1. Normal plot of residuals for DCRA |
2.4.2. Residual Analysis
Rresidualversus run number and residual versus predicted plots of dry crease recovery angle have been shown from Figure 2and 3. The pattern of the residualsshowed that they are normally distributed and the equality of variance does not seem to be violated. 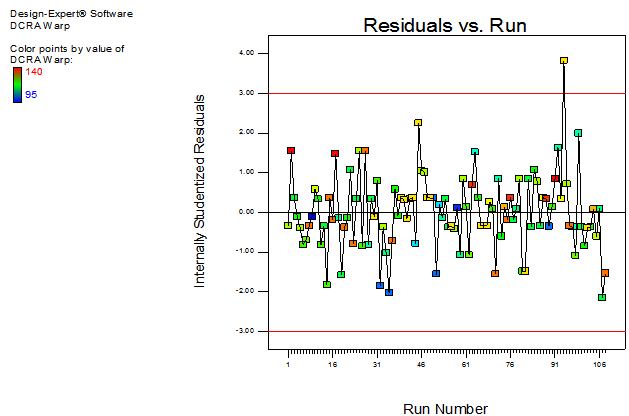 | Figure 2. Residual vs. run number for DCRA |
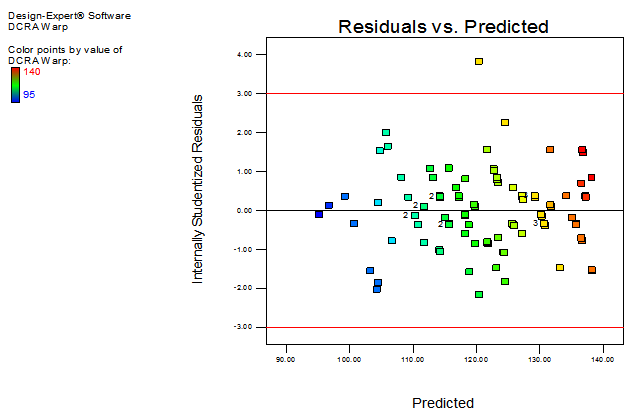 | Figure 3. Residual vs. predicted plot for DCRA |
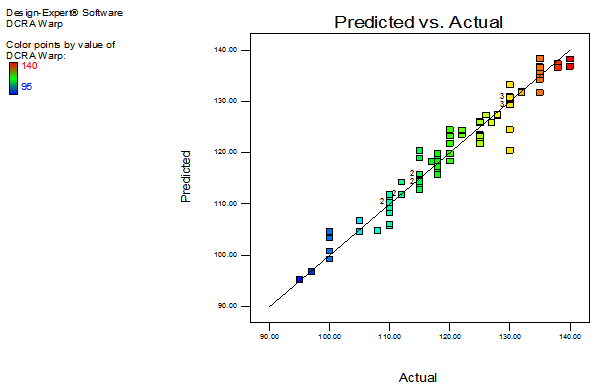 | Figure 4. The predicted vs. actual plot for DCRA |
2.5. Analysis of Variances (ANOVA)
Table 1 shows the summary of ANOVA results ofdry crease recovery angle for single step fixation process of reactive printing and crease resistance finishing. The model p-value implied that the respective model is significant for dry crease recovery angle.As can be seen in Table 1, The "Lack of Fit p-value" of 0.9998 implies the Lack of Fit is not significant relative to the pure error representing that the suggested models are well-fitted to the observed response.. The "Pred R-Squared" of 0.8630 is in reasonable agreement with the "Adj R-Squared" of 0.9189 specifying the respective model is adequate.The actual and predicted plot of dry crease recovery angle has been shown in Figure 4. The actual values are the measured response data for particular run and the predicted values are theresults generated using the approximate functions. It is found that the adequate precision of Dry crease recovery angle is found to be 20.27, which measured the signal to noise ratio is much greater than 4, (Table 1). This indicates the modelis adequate to be used to navigate the design space. Focusing on the model maximizing the “Adjusted R-squared” and the “Predicted R-squared” different process order selection has been made for dry crease recovery angle. The alias structures of the dry crease recovery angle are shown in Table 3.Table 1. Summary of ANOVA results of dry crease recovery angle (DCRA)
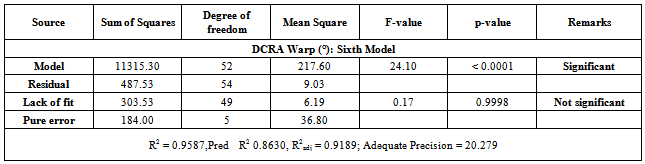 |
| |
|
Table 2. ANOVA for DCRA warp
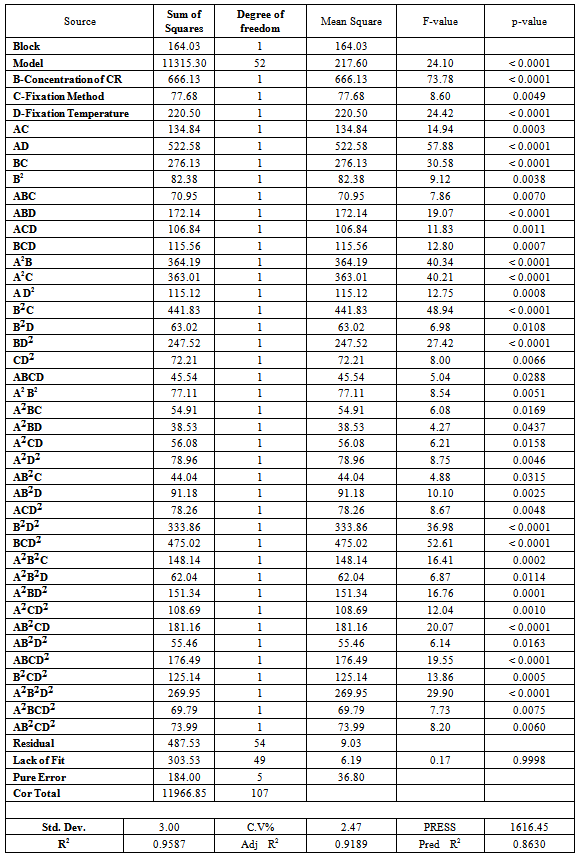 |
| |
|
Table 3. Alias structures for DCRA
 |
| |
|
3. Results and Discussion
3.1. Analysis of Dry Crease Recovery Angle (DCRA)
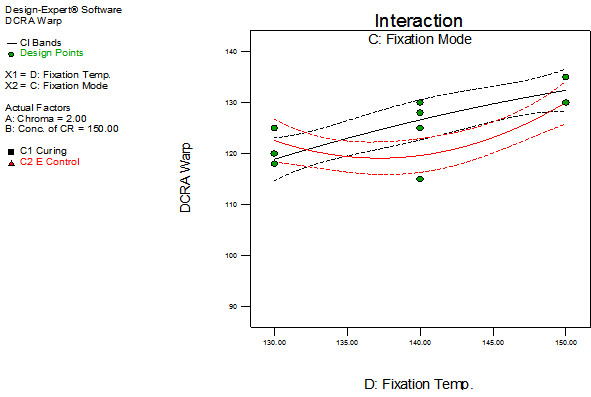
The sixth order model has been selected for the response variable DCRA Warp. The detail of ANOVA of DCRA Warp is shown in Table 2. The Model p-value less than 0.05 implies the model is significant. In this case B, C, D, AC, AD, BC, B2, ABC, ABD, ACD, BCD, A2B, A2C, AD2, B2C, B2D, BD2, CD2, ABCD, A2B2, A2BC, A2BD, A2CD, A2D2, AB2C, AB2D, ACD2, B2D2, BCD2, A2B2C, A2B2D, A2BD2, A2CD2, AB2CD, AB2D2, ABCD2, B2CD2, A2B2D2, A2BCD2, AB2CD2are significant model terms. The graphs of significant model terms for DCRA have been shown from Figure 5 to 15.The graphs of significant model terms revealed that the dry crease revovery angle of the single step fixation process of reactive printing and crease resistance finishing is dependent on the interaction and curvature effect of concentration of crease resistant, fixation mode and fixation temperature.Figure 8 and 9 indicated that the Econtrol process supersedes the conventional curing process for fixation and gives a higher dry crease recovery angle in the single step fixation process. Figure 16illustrates the interaction plot of fixation mode and fixation temperature. The graph clearly shown that the Econtrol process at 130°C gives a higher dry crease recovery angle in the CPF process. The reduced regression equation of dry crease recovery angle has been shown in Equation (1).Whereas, the fitted regression equation has been presented in Equation (2). The alias structures are shown in Table 3.
3.2. Mathematical Model with Significant Variables at α = 0.05
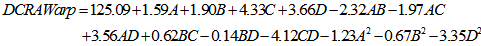 | (1) |
3.3. Fitted Regression Equation of DCRA
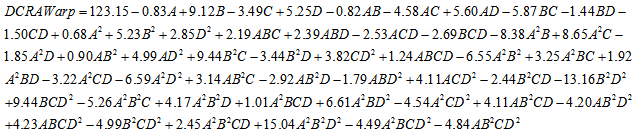 | (2) |
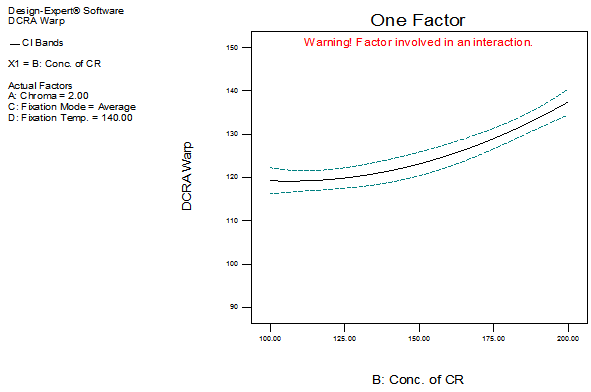 | Figure 5. Effect of B on DCRA warp |
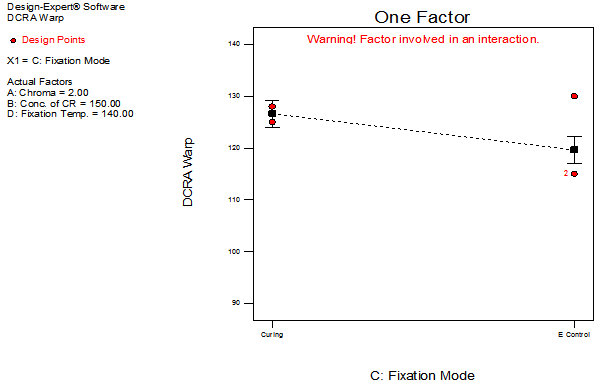 | Figure 6. Effect of C on DCRA warp |
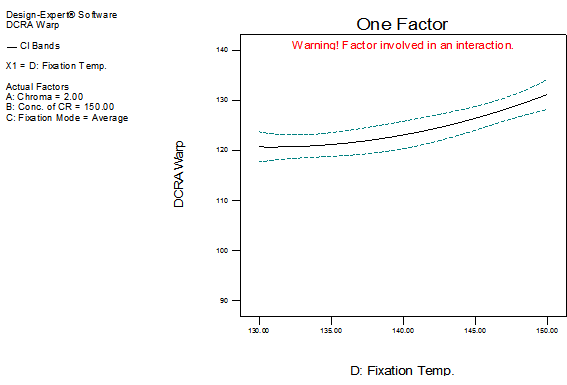 | Figure 7. Effect of D on DCRA warp |
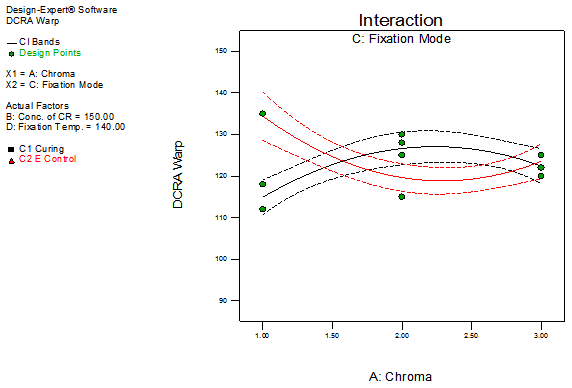 | Figure 8. Interaction plot of AC with respect to DCRA warp |
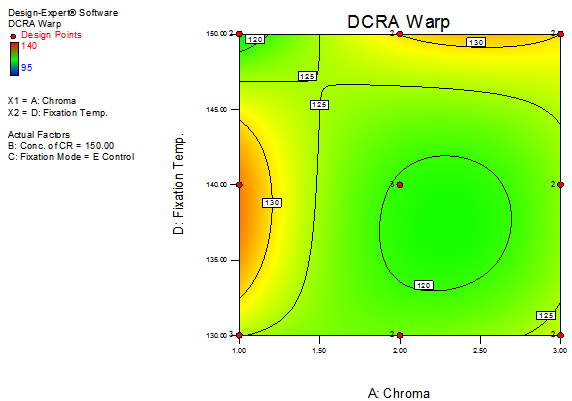 | Figure 10. Contour plot representing DCRA warp versus chroma and fixation temperature |
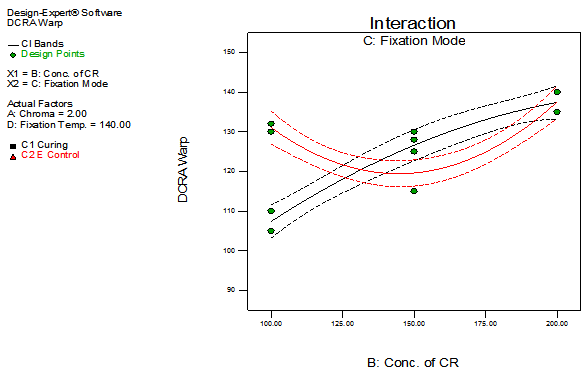 | Figure 11. Interaction plot of BC with respect to DCRA warp |
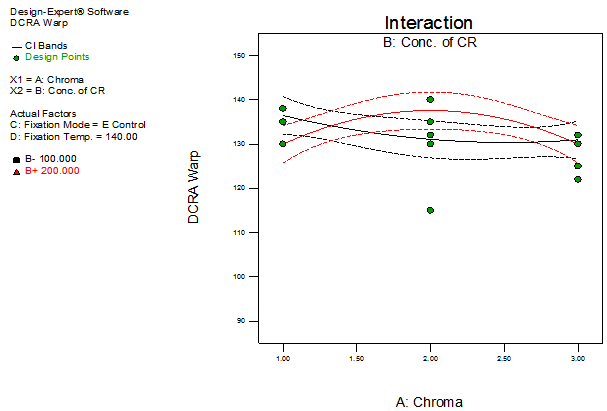 | Figure 12. Interaction plot of AB with respect to DCRA warp |
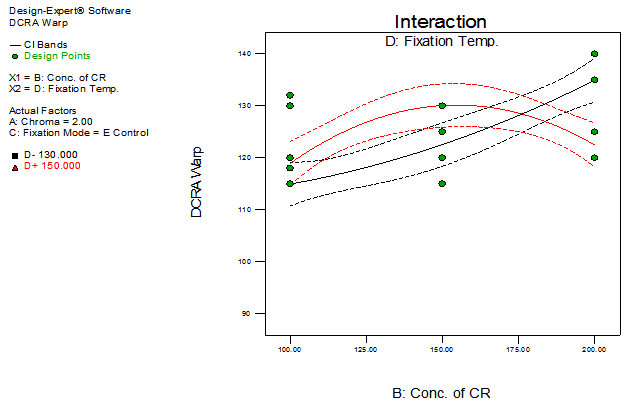 | Figure 13. Interaction plot of BD with respect to DCRA warp |
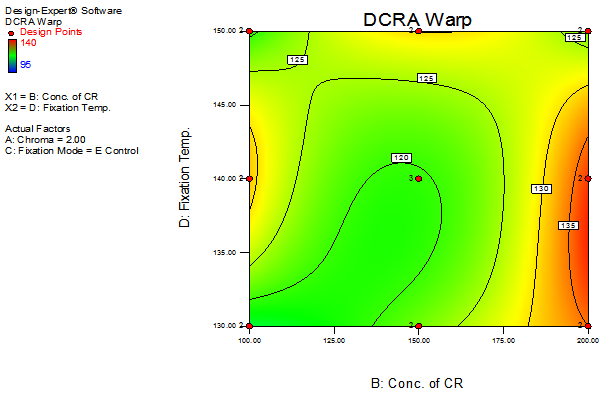 | Figure 14. Contour plot representing DCRA warp versus concentration of CR and fixation temperature |
 | Figure 15. Interaction plot of CD with respect to DCRA warp |
4. Conclusions
The factorial design of experiments for single step fixation process of reactive printing and crease resistance finishing was studied. The quadratic effect of three factors namely, concentration of crease resistant, fixation method and fixation temperature on dry crease recovery angle were identified. The statistical analysis gave a reasonably good fit with an F-value of 24.10 and an R2-value of 0.9587. According to the significance effect obtained in variance analysis, the concentration of crease resistant was the most significant factor for the dry crease recovery angle under the conditions investigated.The information obtained from the mathematical model has been used to create optimal parameters of single step fixation process of reactive printing and crease resistance finishing process.
ACKNOWLEDGEMENTS
The authors wish to express their gratitude to Gul Ahmed Textile Mills Ltd and Clariant Pakistan Ltd, for carrying out the necessary experimental work.
References
| [1] | H. Tavanai1, S. M.Taheri, M. Nasiri, “Modelling of Colour Yield in Polyethylene Terephthalate Dyeing with Statistical and Fuzzy Regression”, Iranian Polymer Journal, 14 (11), 954-967 (2005) |
| [2] | H. Tavanai, A. Z. Hamadani, M. Askari, “Modelling of Colour Yield for Selected Reactive Dyes in Dyeing Cotton Cloth by Two Phase Pad-steam Method”, Iranian Polymer Journal, 15 (3), 207-217(2006) |
| [3] | V. Vassileva, E. Valcheva, Z. Zheleva, “The Kinetic Model of Reactive Dye Fixation on Cotton Fibres”, Journal of the University of Chemical Technology and Metallurgy, 43(3), 323-326 (2008) |
| [4] | F. Asim, M. Mahmood, M. A. Siddiqui, “Optimization of process parameters for simultaneous fixation of reactive printing and crease resistant finishing using desirability function”, International Conference on Systems Engineering and Engineering Management, 1098-1105 (2011) |
| [5] | F. Asim, M. Mahmood, “Multi response optimization of simultaneous fixation of reactive printing and crease resistant finishing using desirability function”, International Journal of Statistics and Applications, 2(6), 126-131 (2012) |
| [6] | F. Asim, M. Mahmood, “Optimization of process parameters for simultaneous fixation of reactive printing and crease resistant finishing”, Journal of Textile and apparel Technology Management, 7(3), Spring (2012) |
| [7] | Y. H. El Hamaky, S. Tawfeek, D. F. Ibrahim, D. Maamoun, S. Gaber, “Printing Cotton Fabrics with Reactive Dyes of High Reactivity from an Acidic Printing Paste”, Coloration Technology, 123(6), 365-373 (2007) |
| [8] | N. S. E. Ahmed, Y. A. Yourself, R. M. El-Shishtawy, A. A. Mousa, “Urea/Alkali Free Printing of Cotton with Reactive Dyes”, Coloration Technology, 122(6), 324-328 (2006) |
| [9] | Y. Yang, V. Naarani, “Effect of Steaming Conditions on Colour and Consistency of Ink-Jet Printed Cotton Using Reactive Dyes”, Coloration Technology, 120(3), 127-131 (2004) |
| [10] | C. W. M. Yuen, S. K. A. Ku, P. S. R. Choi, C. W. Kan, “Study of the Factors Influencing Colour Yield of an Inkjet-Printed Cotton Fabric”, Coloration Technology, 120(6), 320-325 (2004) |
| [11] | Y. Can, M. Akaydin, Y. Turhan, E. Ay, “Effect of Wrinkle Resistance Finish on Cotton Fabric Properties”, Indian Journal of Fibre & Textile Research, 34, 183-186 (2009) |
| [12] | M. S. Hassan, Crease Recovery Properties of Cotton Fabrics Modified by Urea Resins under the Effect of Gamma Irradiation”, Radiation Physics and Chemistry, 78(5), 333-337 (2009) |
| [13] | F. Asim, M. Mahmood, “Reactive Printing & Crease Resistance Finishing of Cotton Fabrics. Part-I Study of Influential Factors by an Experimental Design Approach”, Journal of Textile & Apparel, Technology and Management, 7(1), (2011) |
| [14] | F. Asim, M. Mahmood, “Reactive Printing and Crease Resistance Finishing of Cotton Fabrics-Effects of Fixation Modes by 22.41 Mixed Factorial Design”, International Journal of Textile Science, 1(6), 94-100 (2012) |
| [15] | F. Asim, M. Mahmood, “Effects of Process Parameters on Single Step Fixation of Reactive Printing and Crease Resistance Finishing of Cotton Fabrics using 23 Factorial Design”, International Journal of Textile Science, 2(1), February (2013) |
| [16] | S.M. Mortazavi, M.A. Alsharif, M. Jannesari, “A study on Simultaneous Fixation of Reactive Dye Printing and Crease Resist Finishing on Cotton Fabric (Effect of DMDHEU Concentration, Types of Catalyst and Drying Conditions)”, http://140.134.132.124:8080/dspace/bitstream/2377/3912/1/ce05atc902007000039.pdf |





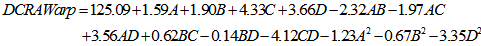
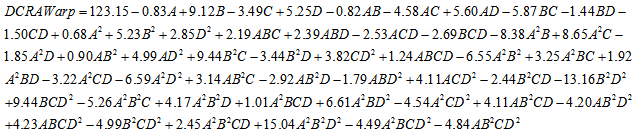










 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

