Kunal Singha1, Subhankar Maity1, Mrinal Singha2, Palash Paul3, Debi Prasad Gon3
1Department of Textile Technology, Panipat Institute of Engineering & Technology, Harayana, India
2Department of Pharmaceutical Chemistry, CU Shah College of Pharmacy & Research, Gujarat, India
3Research scientist, IJIRA, Kolkata, India
Correspondence to: Kunal Singha, Department of Textile Technology, Panipat Institute of Engineering & Technology, Harayana, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Here in this paper a review about the available methods of measuring fiber diameter in a nonwoven structure and its probability distribution has been described. Both offline and online measurement techniques of measuring fibre diameter and analysis of measured data has been discussed. It has been seen from various studies that fibre diameter follows log-normal distribution irrespective of fibre size and manufacturing techniques.
Keywords:
Fiber Diameter, Probability distribution, Log-normal distribution, Fiber size
Cite this paper: Kunal Singha, Subhankar Maity, Mrinal Singha, Palash Paul, Debi Prasad Gon, Effects of Fiber Diameter Distribution of Nonwoven Fabrics on its Properties, International Journal of Textile Science, Vol. 1 No. 1, 2012, pp. 7-14. doi: 10.5923/j.textile.20120101.02.
1. Introduction
The term ‘nonwoven’ arose from more than half a century ago when nonwovens were often regarded as low-price fibrous materials as the substitute of traditional textiles and were generally made from dry laid carded webs using converted textile processing machinery. Especially the yarn formation process was omitted and fabric was developed directly by bonding the fibre web in various ways. Now nonwovens are most vital in various technical textile applications due to their better functionality, specific properties and ease of manufacturing. There are formal definitions of nonwoven proposed by industrial organizations. INDA, North America’s Association of the Nonwoven Fabrics Industry, describes nonwoven fabrics as ‘sheet or web structures bonded together by entangling fibers or filaments, by various mechanical, thermal and/or chemical processes. EDANA, (The European Disposables and Nonwovens Association) defines a nonwoven as ‘a manufactured sheet, web or batt of directionally or randomly orientated fibers, bonded by friction, and/or cohesion and/or adhesion’, but goes on to exclude a number of materials from the definition, including paper, products which are woven, knitted, tufted or stitch- bonded (incorporating binding yarns or filaments), or felted by wet-milling, whether or not additionally needled[1,2].Now-a-days most challenging job in nonwoven industry is to manufacture nonwovens with increasingly smaller fiber diameter. Since the surface area of a fiber scales linearly with the diameter and the volume scales with the square of the diameter, the specific surface area varies inversely with diameter (s∞1/d), leading to higher specific surface areas for finer fibers, which has a greater surface functionalization. So, fiber diameter distribution largely determines the finished web properties, the measurement and control of diameter distribution is of great industrial importance. In addition, the ultimate nonwoven properties such as overall nonwoven strength (related to individual fiber strength, average fiber length, and fiber entanglement density) and porosity play an equally important role in end-use applications. Fiber diameter directly influences the individual fibre strength and porosity. Nonwovens with better surface functionalization find use in a range of applications such as filtration, membrane separation, protective clothing, wound dressings, precession wipes, scaffolds for tissue engineering etc.[3-7]. Electrospinning, melt blowing and spun bonding are most common commercially used processes for nonwoven production by polymer spinning. Electrospinning involves applying a strong electric potential of more than 10 kV to a polymer solution contained in a syringe to force a jet of the solution onto a grounded screen located a few centimeters away. Rapid evaporation of the solvent results in a nonwoven material of ultra-fine fibers of diameter in nanometer range[1-2, 8-9].During melt blowing, fibers are produced in a single step by extruding a polymer melt through an orifice die and drawing down the extrudate with a jet of hot air (typically at the same temperature as the molten polymer). In general, these commercial products are composed of fibers with average diameters of 1-7μm[1-2]. Spun bonding involves one of the three generic technologies: melt, dry or wet spinning. Melt spinning involves a thermoplastic fiber forming polymer and extrusion into cold air or an alternative gas, where the cooling and solidification of the filament is accomplished. Dry spinning involves continuous extrusion of a fiber forming polymer into a heated chamber to remove the solvent, leaving the solid filament. Wet spinning involves continuous extrusion of a solution of the fiber forming polymer into a liquid coagulating medium where the polymer is regenerated. The fiber diameter is ranged between 1 and 50 μm but preferred range is between 15 and 35 μm[1-2].
2. Methods for Measuring Fiber Diameter
There are instruments and methods, the most widely used instrumental methods are Sirolan LaserScan , OFDA , Projection microscopy, Scanning Electron microscopy, Ensemble laser diffraction etc. A brief about these methods are following.
2.1. Sirolan Laser Scan
The Laser Scan instrument measures fibers by dispersing individual snippets (2 mm lengths of fiber) in a solution of isopropanol and water and this fluid transports the fibers through a glass cell where each one intersects a laser beam. The Laser Scan measures the change in the signal generated when the shadow cast by the fiber snippets falls on a light detector. The signals, which are directly proportional to the fiber diameter, are recorded electronically and analyzed almost instantaneously by computer. This method is not useful for measuring the diameter of a fiber in a nonwoven structure. It is useful for measuring individual fiber diameter[11].
2.2. Optical Fibre Diameter Analyser (OFDA)
The OFDA instrument is essentially an automatic microscope set above. A prepared slide of fiber mat is kept under the lens. The instrument magnifies and captures images of the individual fibers using a video camera.It marks the edges of the fibers and measures the distance either vertically or horizontally between the sides of the fibers.Because it knows the slope of the fiber it can calculate the shortest distance between the sides, which is the diameter. | Figure 1. OFDA |
The instrument can measure mean fiber Diameter (MFD), Coefficient of Variation of Fiber Diameter (CVD), Standard deviation (SD). The histogram of the measured data can also be plotted by computer interface[11,12].
2.3. Microprojection
The projection microscope provides the only primary reference method available for the direct measurement of the mean fiber diameter and its distribution. The diameter and distribution values have been determined using the Projection Microscope. Projected fiber images are individually measured at 500X magnification. However, this method is time consuming and expensive and only used occasionally now a days for special jobs[11]. | Figure 2. Projection microscope |
 | Figure 3. Airflow instrument |
2.4. Airflow
Airflow measures the flow of air through a sample and provides an indirect measurement of average fiber diameter. The principle of the Airflow method is to apply a constant air pressure to a fixed mass of fiber in a standard volume chamber and to measure the resulting flow of air through the sample. The surface area of the fibers creates a resistance to the flow of air, and this flow can be accurately measured on an Airflow meter. Finer fibers cause greater resistance to the flow of air than coarse fiber. It is possible to calibrate the Airflow meter to produce very accurate results. It is quick, simple, inexpensive and accurate on most fibers and specially wool types. But this method gives only average fiber diameter. So it is not useful to produce the histogram[11].
2.5. Scanning Electron Microscope (SEM)
The sample is imaged by scanning electron microscopy (SEM). Image is shown in Figures. The image is processed on software that permitted the investigator to identify two points at opposite ends of a fiber diameter, and then to record the diameter for further processing. A few such designated diameters are shown in Figure 4. The individual fibers were identified in the images, their diameters measured, cumulative probability distributions plotted, and histograms of the number of fibers within selected class interval of fiber diameters can be prepared[13]. | Figure 4. SEM image of typical melt blown nonwoven |
2.6. Ensemble Laser Diffraction Technique
Ensemble laser diffraction (ELD) provides a method for measuring fiber diameter distribution both while the fiber formation process is still taking place (online) and after the fiber has been formed (offline). Online measurements are important for understanding, controlling and modeling the production process. Ensemble laser diffraction (ELD) works by passing a collimated laser beam through a group of fibers and measuring the scattering of the transmitted light. The radial scattering profile is directly related to the diameter distribution of the fibers present within the sampling volume. The sampling volume for the FibrSizr unit is a cylinder that is 12 millimeters in diameter and up to 200 millimeters in length. The sample, either a fiber mat or fiber stream, can lie in almost any orientation relative to the sampling volume. Figure5 illustrates the use of the FibrSizr unit. The scattering of the light is measured using a central sensor and a series of concentric sensor arcs. The forward scattering of the light is used to measure the fiber diameter distribution. The calculation scheme is based on the scattering data. The raw scattering data are taken at the detector, and then the data are sent to a computer for analysis. A multiple regression technique is used to compute what fiber diameter distribution would produce the observed laser scattering. Since this method is based on the accuracy of the scattering model, calibration is necessary. The manufacturer of the unit conducted an extensive calibration of the scattering model wherein the ELD measurements were verified by both scanning electron microscopy (SEM) and optical microscopy. It was found that the laser scattering technique gave very good agreement with both SEM and optical measurements[14].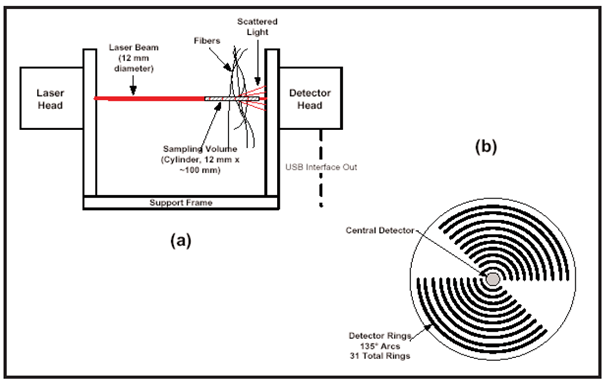 | Figure 5. FibrSizr unit |
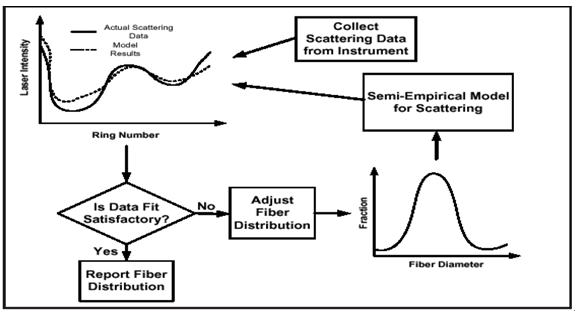 | Figure 6. Data processing system |
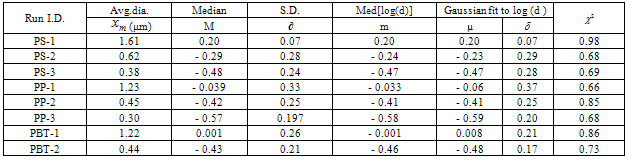
Table 1. Experimental data[15]
 |
| |
|
3. Fiber Diameter Distribution
At least 250 fiber measurements from a melt blown PP nonwoven mat from more than 20 SEM images were used in order to ensure reproducible statistics when measuring fiber size distributions. Fiber diameters were measured by image processing software (ImageJ, NIST). Fiber diameters were measured from SEM images by drawing straight lines along the diagonals of an image (to ensure fibers were not counted twice) and measuring fibers that crossed the lines. To generate reliable statistics, fibers were imaged from different parts of a 1 cm × 1 cm sample area. In addition, the fibers lying outside the focal plane were not used in the statistical analysis[15].If there are n no. of observations and values are 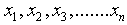 . Then1. The mean of fiber diameter
. Then1. The mean of fiber diameter 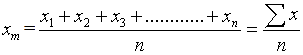 2. Median is the middle most value of the smallest and largest value of observation cab be defined by The single middle value if n is odd or the average of middle two values if n is even3. Standard Deviation
2. Median is the middle most value of the smallest and largest value of observation cab be defined by The single middle value if n is odd or the average of middle two values if n is even3. Standard Deviation 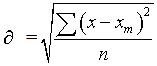 4. Chi-Square value
4. Chi-Square value  In the table1 below the measured parameters are listed.
In the table1 below the measured parameters are listed.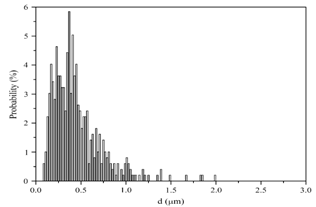 | Figure 7. Fiber diameter distributions from the PP melt blowing run[15] |
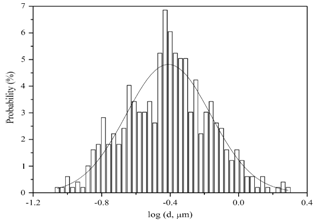 | Figure 8. Lognormal fit of diameter distribution[15] |
The histograms were constructed using class sizes that produced approximately 50 classes across the entire distribution. We found that this led to a good compromise between smaller class sizes which results in smoothing of the shape of the distribution and larger class sizes which do not capture the nature of the distribution. Consequently, the choice of class size can impact the 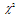 value that is reported in Table 1, which is representative of the goodness of fit of the log-normal distribution function to the experimental data. The plotted Histogram is shown below in the figure: 7 and it also depicts that the distribution curve is asymmetric (positively skewed) and has a tail at the large diameter end. An asymmetric distribution implies that as one moves away from the peak of the distribution, the probability of observing the independent variable does not reduce linearly. From a statistical perspective, the fiber diameter is an independent variable and the probability of observing a particular fiber size is distributed asymmetrically about the most fiber diameter. Figure: 8 shows the distribution plotted versus the logarithm of the fiber diameter (log(x)) as the independent variable. This is a reasonably symmetric curve with the arithmetic mean (μ) of log(x) being nearly equal to the median m. This is the characteristic features of the normal distribution.
value that is reported in Table 1, which is representative of the goodness of fit of the log-normal distribution function to the experimental data. The plotted Histogram is shown below in the figure: 7 and it also depicts that the distribution curve is asymmetric (positively skewed) and has a tail at the large diameter end. An asymmetric distribution implies that as one moves away from the peak of the distribution, the probability of observing the independent variable does not reduce linearly. From a statistical perspective, the fiber diameter is an independent variable and the probability of observing a particular fiber size is distributed asymmetrically about the most fiber diameter. Figure: 8 shows the distribution plotted versus the logarithm of the fiber diameter (log(x)) as the independent variable. This is a reasonably symmetric curve with the arithmetic mean (μ) of log(x) being nearly equal to the median m. This is the characteristic features of the normal distribution.
3.1. Testing of Goodness of Fit by Chi-Square Method
In fig 8, a normal (Gaussian) distribution profile shows a good fit (with a reasonable 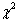 value) to the log(x) data where the probability density function for a normal distribution is given by,
value) to the log(x) data where the probability density function for a normal distribution is given by,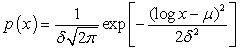 A chi-square distribution with (k - 1) degrees of freedom where k is the number of non-empty class. is hypothesized that the data are from a population with the specified distribution is rejected if
A chi-square distribution with (k - 1) degrees of freedom where k is the number of non-empty class. is hypothesized that the data are from a population with the specified distribution is rejected if 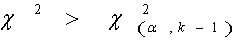 Where
Where 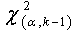 is the chi-square percent point function with k -1 degrees of freedom at a significance level of α.Here in our paper k=50. So Degree or freedom = 50-1= 49.
is the chi-square percent point function with k -1 degrees of freedom at a significance level of α.Here in our paper k=50. So Degree or freedom = 50-1= 49.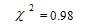 The value of
The value of 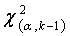 can be obtained from the standard
can be obtained from the standard 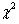 chart, where
chart, where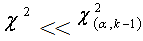 for this higher value of degree of freedom and for all confidence level. Thus, the Chi-square test can not be rejected and it states that the fiber diameter distribution for the melt blowing run PP closely resembles a log-normal distribution[15-17].
for this higher value of degree of freedom and for all confidence level. Thus, the Chi-square test can not be rejected and it states that the fiber diameter distribution for the melt blowing run PP closely resembles a log-normal distribution[15-17].
3.2. Some Other Observations
This analysis was repeated for some other melt blowing runs from (approximately 50 classes were used for the log(x) histogram of each sample). In all cases the mean (μ) and median of log(x) are nearly equal, as shown in the table: 2, and a good fit is obtained for a Gaussian distribution with fitting parameters μ and σ. Thus, all the melt blown fiber mats can be said to follow log-normal distributions and, in fact, it is observed the melt blowing process to produce fibers which exhibit the features of the log-normal distribution in all cases regardless of average fiber diameter. It suggests that the basic fiber formation mechanism does not change substantially when producing nanofibers compared to those much larger in diameter.
3.3. A Comparison between the Sizes of Distribution
Fig.9a, 9b, 9c compares the Gaussian fits to the fiber size distributions for the largest and smallest fibers from PS, PP and PBT (same samples as those shown in table 2). It appears that there is no apparent dependence of the width of the distribution on average fiber diameter (width of PS increases, PBT is about the same and PP decreases in going to smaller fiber diameters). The width of the distribution depends on the Variance, which is defined by the square of Standard Deviation. So the value of Standard Deviation be more, more will be the width of the distribution. The PS-1 sample distribution is the narrowest distribution as it has smallest value of Standard Deviation In general, there is interest in controlling both the average fiber size and the width of the fiber size distribution as they control both the average pore size and the pore size distribution, which are important properties of nonwovens (e.g. in filtration applications). Fundamentally, it makes sense that this distribution is a manifestation of the dynamic aspects of the fiber as it whips across the air stream. This whipping action produces a dynamic drag/extensional force which in turn produces a variable fiber size and defines the shape of the distribution[15].Table 2. Average fiber diameters and log-normal distribution parameters[15]
 |
| |
|
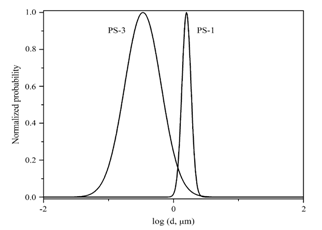 | Figure 9(a). Normalized Gaussian fits to log(x) data for PS melt blowing runs[15] |
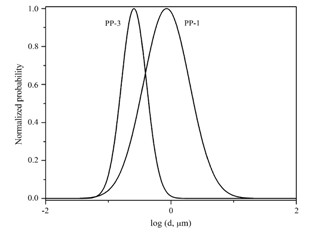 | Figure 9(b). Normalized Gaussian fits to log(x) data for PP melt blowing runs[15] |
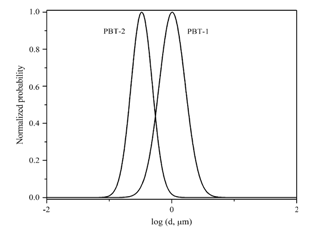 | Figure 9(c). Normalized Gaussian fits to log(x) data for PBT melt blowing runs[15] |
3.4. Comparison among Different Sample Having Same Mean Fiber Dia
Here in the figure: 10 the simulated image of four different fabric sample of same mean fiber diameter has been shown. Their diameter distributions of Log normal fit has been plotted as shown in figure: 11. | Figure 10. Simulated image of constant dia[18] |
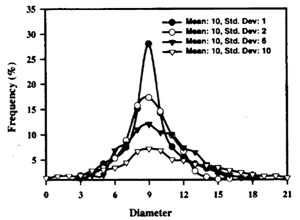 | Figure 11. Log normal fit of four different fabric samples[18] |
Though there mean fiber diameter is same as the values of S.D. are different the distribution patterns has been varied. The minimum S.D. value gives narrowest distribution with highest peak[18-22].
3.5. Comparison among Needle Punched, Melt Blown and Spun Bond Nonwovens
The simulated image of three different nonwoven sample (Needle punched Carded web, Melt Blown and Spun Bonded) has been shown in fig.12[18]. The diameter distribution plot of these samples has been shown in figure: 13[18].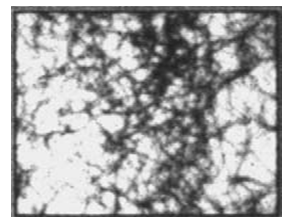 | Figure 12(a). Sample-A Carded web needle punched |
 | Figure 12(b). Sample-B Melt Blown |
 | Figure 12(c). Sample-C Spun Bonded |
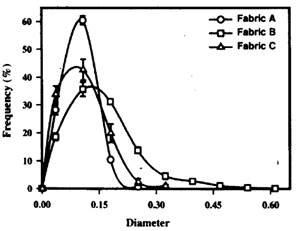 | Figure 13. Diameter Distribution of three samples[18] |
All three samples have more or less same mean fiber diameter. But Sample A has minimum variation in diameter so it gives narrowest distribution. Sample B has maximum variations in diameter so it gives widest distribution. Sample C has a variation value between that of the Sample A and Sample B so it gives medium distribution[18,21,23-24].
4. Conclusions
By this review paper we conclude of some of the important points as following:[a] Fiber diameter distribution in nonwoven structure gives the best fit to the standard Log-Normal curve.[b] The basic fiber formation mechanism does not change substantially when producing nanofibers compared to those much larger in diameter.[c] The width of the distribution mainly depends on the Variations of fiber diameter from the mean value.[d] Both mean fiber size and width of the fiber size distribution should be controlled simultaneously to get the specific property of nonwoven fabric.
References
| [1] | Russel SJ; Hand book of Nonwovens, Woodhead Publishing Ltd, England (2007). |
| [2] | Albrecht W, Fuchs H, Kittelmann W; Nonwoven Fabrics, Weinheim (2003) WILEY-VCH Verlag GmbH & Co, KGaA. |
| [3] | Edward CG; Primer On Nonwoven Fabric Filtration; Textile World, March/April (2009). |
| [4] | Chang WK, Hu AYJ, Horng RY, Tzou WY; Membrane bioreactor with nonwoven fabrics as solid–liquid separation media for wastewater treatment; Desalination (2006) 202: 122–128. |
| [5] | Pause B; Nonwoven Protective Garments with Thermo-Regulating Properties; Journal of Industrial Textiles, October (2003) 33: 93-99. |
| [6] | Mao N, Russell SJ; Nonwoven Wound Dressings; Textile Progress, (2004) 4 (36):1-57. |
| [7] | Edwards SL, Mitchell W, Matthews JB, Ingham E, Russell SJ; Design of Nonwoven Scaffold Structures for Tissue Engineering of the Anterior Cruciate Ligament; AUTEX Research Journal, June (2004) 4: 86-94. |
| [8] | Hutmacher WD, Dalton DP; Melt Electrospinning; Chemistry Asian Journal (2011) 6: 44-56. |
| [9] | Huang ZM, Zhang YZ, Kotaki M, Ramakrishna S ; A review on polymer nanofibers by electrospinning and their applications in nanocomposites; Composites Science and Technology (2003) 63: 2223-2253. |
| [10] | Terezie Zapletalova, Stephen Michielsen, Behnam Pourdeyhimi; Polyether Based Thermoplastic Polyurethane Melt Blown Nonwovens; Freudenberg Nonwovens (North America) (1999) 122-125. |
| [11] | McColl A, McColl Y, Methods for Measuring Microns. Testing Laboratories, Inc, Denver |
| [12] | K. Qi, C. J. Lupton, F. A. Pfeiffer and D. L. Minikhiem; Evaluation of the optical fibre diameter analyser (OFDA) for measuring fiber; J Anim Sci (1994) 72:1675-1679. |
| [13] | Peter P. Tsai, WeiChen, J. Reece Roth; Investigation of the Fiber, Bulk, and Surface Properties of Meltblown and Electrospun Polymeric Fabrics; Freudenberg Nonwovens (North America) (2002): 134-138. |
| [14] | Eric M. Moore, Robert. L. Shambaugh, and Dimitrios V. Papavassiliou; Ensemble Laser Diffraction forOnline Measurement of Fiber Diameter Distribution Duringthe Melt Blowing Process; INJ; Summer (2004) 42-47. |
| [15] | Christopher J. Ellison, Alhad Phatak, David W. Giles, Christopher W. Macosko, Frank S. Bates; Melt blown nanofibers: Fiber diameter distributions and onset of fiber breakup; Polymer (2007) 48: 3306-3316. |
| [16] | Douglas C. Montgomery, George C. Runger, Applied Statistics and Probability for Engineers, (2003) Inc Third Edition; John Wiley & Sons. |
| [17] | Murray R. Spiegel, John J. Schiller, R. Alu Srinivasan, Probability and Statistics, Third Edition, (2009) Schaum’s Outline Series; The McGraw-Hill Companies Inc. |
| [18] | Pourdeyhimi B. and Dent R.; Measuring Fiber Diameter Distribution in Nonwovens; Textile Research Journal (1999) 69: 233. |
| [19] | Pourdeyhimi B, Ramanathan R. and Dent R.; Measuring Fiber Orientation in Nonwovens: Part I: Simulation; Textile Research Journal (1996) 66: 713. |
| [20] | Raoul Farer, Abdelfattah M. Seyam, Tushar K. Ghosh, Eddie Grant, Subhash K. Batra; Meltblown Structures Formed by a Robotic and Meltblowing Integrated System: Impact of Process Parameters on Fiber Orientation and Diameter Distribution; Textile Research Journal (2002) 72: 1033. |
| [21] | Pourdehyhimi B., Dent R., Jerbi A.,Tanaka S., Deshpande A., Measuring Fiber Orientation in Nonwovens Part V: Real Webs; Textile Research Journal (1999) 69: 185. |
| [22] | Barella A., Measuring Fiber Diameter Distribution in Nonwovens; Textile Research Journal (2000) 70: 277. |
| [23] | Pourdeyhimi B, Ramanathan R. and Dent R.; Measuring Fiber Orientation in Nonwovens: Part I: Simulation; Textile Research Journal (1996) 66: 713. |
| [24] | Rita Salvado, Jacques Silvy and Jean-Yves Drea; Relationship between Fibrous Structure and Spunbond Process; Textile Research Journal (2006) 76: 805. |







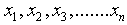 . Then1. The mean of fiber diameter
. Then1. The mean of fiber diameter 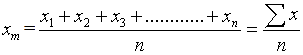 2. Median is the middle most value of the smallest and largest value of observation cab be defined by The single middle value if n is odd or the average of middle two values if n is even3. Standard Deviation
2. Median is the middle most value of the smallest and largest value of observation cab be defined by The single middle value if n is odd or the average of middle two values if n is even3. Standard Deviation 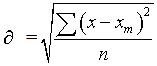 4. Chi-Square value
4. Chi-Square value  In the table1 below the measured parameters are listed.
In the table1 below the measured parameters are listed.

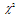 value that is reported in Table 1, which is representative of the goodness of fit of the log-normal distribution function to the experimental data. The plotted Histogram is shown below in the figure: 7 and it also depicts that the distribution curve is asymmetric (positively skewed) and has a tail at the large diameter end. An asymmetric distribution implies that as one moves away from the peak of the distribution, the probability of observing the independent variable does not reduce linearly. From a statistical perspective, the fiber diameter is an independent variable and the probability of observing a particular fiber size is distributed asymmetrically about the most fiber diameter. Figure: 8 shows the distribution plotted versus the logarithm of the fiber diameter (log(x)) as the independent variable. This is a reasonably symmetric curve with the arithmetic mean (μ) of log(x) being nearly equal to the median m. This is the characteristic features of the normal distribution.
value that is reported in Table 1, which is representative of the goodness of fit of the log-normal distribution function to the experimental data. The plotted Histogram is shown below in the figure: 7 and it also depicts that the distribution curve is asymmetric (positively skewed) and has a tail at the large diameter end. An asymmetric distribution implies that as one moves away from the peak of the distribution, the probability of observing the independent variable does not reduce linearly. From a statistical perspective, the fiber diameter is an independent variable and the probability of observing a particular fiber size is distributed asymmetrically about the most fiber diameter. Figure: 8 shows the distribution plotted versus the logarithm of the fiber diameter (log(x)) as the independent variable. This is a reasonably symmetric curve with the arithmetic mean (μ) of log(x) being nearly equal to the median m. This is the characteristic features of the normal distribution. value) to the log(x) data where the probability density function for a normal distribution is given by,
value) to the log(x) data where the probability density function for a normal distribution is given by,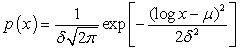 A chi-square distribution with (k - 1) degrees of freedom where k is the number of non-empty class. is hypothesized that the data are from a population with the specified distribution is rejected if
A chi-square distribution with (k - 1) degrees of freedom where k is the number of non-empty class. is hypothesized that the data are from a population with the specified distribution is rejected if 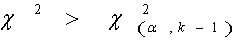 Where
Where 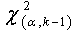 is the chi-square percent point function with k -1 degrees of freedom at a significance level of α.Here in our paper k=50. So Degree or freedom = 50-1= 49.
is the chi-square percent point function with k -1 degrees of freedom at a significance level of α.Here in our paper k=50. So Degree or freedom = 50-1= 49.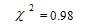 The value of
The value of 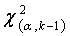 can be obtained from the standard
can be obtained from the standard 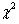 chart, where
chart, where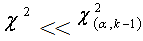 for this higher value of degree of freedom and for all confidence level. Thus, the Chi-square test can not be rejected and it states that the fiber diameter distribution for the melt blowing run PP closely resembles a log-normal distribution[15-17].
for this higher value of degree of freedom and for all confidence level. Thus, the Chi-square test can not be rejected and it states that the fiber diameter distribution for the melt blowing run PP closely resembles a log-normal distribution[15-17].








 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
