M. O. Nasiru, S. O. Olanrewaju, O. A. Adejumo O.
Department of Statistics, Faculty of Science, University of Abuja, Abuja, Nigeria
Correspondence to: M. O. Nasiru, Department of Statistics, Faculty of Science, University of Abuja, Abuja, Nigeria.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper is about the comparison of the methods of estimation of parameters in integer valued first order autoregressive (INAR(1)) model.The study compares two estimation methods, Yule-Walker (YW) and Conditional Least Squares (CLS), for the class of INAR(1) model. Monte Carlo simulations were conducted to evaluate the performance of these estimators under different parameter values and sample sizes. The simulations were done with the aid of R statistical package. All results were based on 1000 runs. A range of (INAR(1)) parameters and different lengths of history were considered. We considered parameter values of  = 0.2, 0.6, and 0.8, and ample sizes of n=30, 90, 120, and 600 for the simulations. The results showed that CLS produced lower standard errors than YW for all selected sample sizes, and this improvement became more pronounced as the parameter values increased. Both CLS and YW produced lower standard errors as the sample sizes increased. The simulation findings were corroborated when applied to the COVID-19 death series in Nigeria in 2021.
= 0.2, 0.6, and 0.8, and ample sizes of n=30, 90, 120, and 600 for the simulations. The results showed that CLS produced lower standard errors than YW for all selected sample sizes, and this improvement became more pronounced as the parameter values increased. Both CLS and YW produced lower standard errors as the sample sizes increased. The simulation findings were corroborated when applied to the COVID-19 death series in Nigeria in 2021.
Keywords:
Estimation, Autoregressive, INAR(1), YW estimation, CLS estimation, Simulation, COVID-19
Cite this paper: M. O. Nasiru, S. O. Olanrewaju, O. A. Adejumo O., Comparison of the Methods of Estimation of Parameters in Integer-Valued First Order Autoregressive (INAR(1)) Model, International Journal of Statistics and Applications, Vol. 15 No. 1, 2025, pp. 23-28. doi: 10.5923/j.statistics.20251501.03.
1. Introduction
Recently, there has been increased attention in the literature towards Integer Autoregressive Moving Average (INARMA) models. This interest stems from the capability of INARMA models to model and forecast Time Series Count data in various scientific fields such as medical, environmental, and financial applications, particularly for low frequency count with overdispersed data.A time series is a collection of observations  , observed sequentially with time t. For continuous time series, the observations are measured continuously over some time interval, for example,
, observed sequentially with time t. For continuous time series, the observations are measured continuously over some time interval, for example, 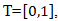 while for discrete-time series, the observations are measured at sequential integer values over fixed time intervals.The primary objective of time series analysis is to establish a hypothetical probability model, the time series model, to represent the data. Once an appropriate family of models is chosen, it becomes possible to estimate the parameters in the models, assess the goodness-of-fit to the data, and potentially use the proposed models to enhance understanding of the underlying mechanism. Upon obtaining a satisfactory model, it can be utilized for further study, such as making predictions for future observations or applying it in a specific field. A time series model for the observed data
while for discrete-time series, the observations are measured at sequential integer values over fixed time intervals.The primary objective of time series analysis is to establish a hypothetical probability model, the time series model, to represent the data. Once an appropriate family of models is chosen, it becomes possible to estimate the parameters in the models, assess the goodness-of-fit to the data, and potentially use the proposed models to enhance understanding of the underlying mechanism. Upon obtaining a satisfactory model, it can be utilized for further study, such as making predictions for future observations or applying it in a specific field. A time series model for the observed data  can be interpreted as a specification of a sequence of correlated random variable
can be interpreted as a specification of a sequence of correlated random variable  of which
of which  is postulated to be a realization. Discrete variate time series for counts occur in various contexts, including counts of events (e.g., road accidents, births, or deaths) and counts of individuals (e.g., people in a queue). The INARMA model was originally introduced in the 1980s by Kenzie [13] and Al-Osh and [1], and it has gained significant attention for forecasting time series of counts over the last three decades. This model has been shown to be analogous to well-known conventional time series models, namely Autoregressive Moving Average (ARMA) models [3], for modeling continuous data.The field of modeling discrete-valued time series remains a challenging and underdeveloped area of research in time series analysis due to the integer nature of variate values, which renders traditional representations of dependence either impossible or impractical. Previous attempts to develop suitable models for discrete-valued time series have been imaginative, but recent efforts by [7] and [6] have contributed to the development of models appropriate for discrete-valued time series.The Integer valued Autoregressive (INAR) models are a type of time series model that is used to analyze and forecast integer-valued time series data. The model is based on the idea that the current value of the time series is a function of past values, and the error term is an integer-valued random variable. Estimating the parameters of an INAR model is crucial for making accurate predictions and understanding the underlying dynamics of the time series. Several approaches have been proposed in the literature to develop suitable methods for estimating INAR-type models, with the aim of providing accurate and reliable estimates.[15], proposes a new method for estimating the parameters of integer-valued autoregressive (INAR) models using the stochastic approximation algorithm (SAA). The traditional method for estimating the parameters of INAR models is based on the maximum likelihood estimation (MLE) approach, which involves solving a non-linear optimization problem. However, this approach can be computationally intensive and may not be efficient for large datasets. The authors proposed using the SAA, which is a stochastic optimization algorithm that can be used to estimate the parameters of INAR models in a more efficient manner. The SAA algorithm is based on the idea of iteratively updating the parameters using the gradient of the log-likelihood function. The authors demonstrate the effectiveness of their proposed method using simulation studies and real-world data. They show that their method can converge to the true parameter values more quickly than traditional MLE methods, especially when the sample size is large.[9], proposes a Bayesian approach that uses a Markov Chain Monte Carlo (MCMC) method to estimate the parameters of an INAR model with missing values. The MCMC algorithm is based on a fully conditional specification, which allows for efficient estimation and prediction of the INAR model. The authors demonstrate that their method can accurately estimate the parameters of the INAR model even when some of the data points are missing, they show that their Bayesian estimation method outperforms traditional maximum likelihood estimation methods in terms of estimation accuracy. They also demonstrate that their method can provide accurate predictions for future values of the time series, even when there are missing values in the data.[10], proposes a particle filtering approach for estimating the state of integer-valued autoregressive (INAR) models with non-linear and non-Gaussian noise. INAR models are widely used to model time series data that consist of integer-valued observations, but they can be challenging to estimate due to the non-linearity and non-Gaussianity of the noise. The authors emphasized that the traditional methods for estimating INAR models rely on maximum likelihood estimation (MLE) or Bayesian inference, but these methods can be computationally intensive and may not perform well when the noise is non-linear or non-Gaussian. The authors propose using particle filtering, a Monte Carlo method that can be used to approximate the posterior distribution of the state variables in INAR models. They develop a novel particle filtering algorithm that can handle non-linear and non-Gaussian noise by using a combination of importance sampling and resampling techniques. They show that their algorithm can accurately estimate the state variables of INAR models with non-linear and non-Gaussian noise, even when the sample size is small. They demonstrate the effectiveness of their algorithm using simulation studies and real-world data. They show that their algorithm can outperform traditional MLE methods and other particle filtering algorithms when the noise is non-linear or non-Gaussian.[16], proposes a novel neural network-based method for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose using a neural network (NN) to estimate the parameters of INAR models, which can be more efficient and effective than traditional methods. The authors develop a neural network architecture that consists of two parts: an encoder network that maps the input data to a latent space, and a decoder network that generates the output data. The encoder network is trained to minimize the mean squared error between the predicted and actual values of the input data, while the decoder network is trained to minimize the mean squared error between the predicted and actual values of the output data. The authors demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with a large number of parameters, and can outperform traditional MLE methods in terms of computational efficiency and accuracy.[11], proposes a hybrid Bayesian-neural network approach for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose a hybrid approach that combines the strengths of Bayesian inference and neural networks to estimate the parameters of INAR models. The Bayesian component is used to provide a flexible and robust framework for modeling the uncertainty in the parameter estimates, while the neural network component is used to improve the accuracy and efficiency of the estimation. The authors develop a hybrid algorithm that consists of two main steps: first, a Bayesian neural network is trained to estimate the parameters of the INAR model using a Markov chain Monte Carlo (MCMC) algorithm; second, the posterior distribution of the parameters is used to estimate the conditional mean and variance of the model. They demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with complex structures, and can outperform traditional Bayesian methods in terms of computational efficiency and accuracy. They also demonstrate the robustness of their method by comparing it to other Bayesian methods and neural network-based methods. They show that their method can provide more accurate and robust estimates of the parameters of INAR models, even when the data is noisy or has missing values.[5], compares the performance of different methods for estimating the parameters of integer-valued autoregressive (INAR) models. The authors compare the performance of five different methods for estimating INAR models: maximum likelihood estimation (MLE), Bayesian inference using Markov chain Monte Carlo (MCMC), Bayesian inference using Laplace approximation, neural network-based estimation, and a hybrid method that combines MLE and MCMC. They use a simulation study to evaluate the performance of each method in terms of accuracy, computational efficiency, and robustness. They also compare the performance of each method using real-world data. The results show that the Bayesian inference using MCMC method performs well in terms of accuracy and robustness, but it is computationally intensive. The neural network-based estimation method is computationally efficient, but it may not perform as well as the Bayesian methods in terms of accuracy. The hybrid method combines the strengths of MLE and MCMC, but it may not perform as well as the Bayesian methods in terms of robustness. The authors also find that the choice of method depends on the specific characteristics of the data, such as the sample size, the number of parameters, and the level of noise in the data.This paper aim to compare two different estimation methods for the class of INAR(1) model. The specific objectives are:i. Compare the performances of Yule-Walker and Conditional Least Squares estimators for the class of INAR(1) model.ii. Assess the sensitivity of the results to data scarcity and history length.iii. Examine the practical validity, and applicability of these findings on real life data.
is postulated to be a realization. Discrete variate time series for counts occur in various contexts, including counts of events (e.g., road accidents, births, or deaths) and counts of individuals (e.g., people in a queue). The INARMA model was originally introduced in the 1980s by Kenzie [13] and Al-Osh and [1], and it has gained significant attention for forecasting time series of counts over the last three decades. This model has been shown to be analogous to well-known conventional time series models, namely Autoregressive Moving Average (ARMA) models [3], for modeling continuous data.The field of modeling discrete-valued time series remains a challenging and underdeveloped area of research in time series analysis due to the integer nature of variate values, which renders traditional representations of dependence either impossible or impractical. Previous attempts to develop suitable models for discrete-valued time series have been imaginative, but recent efforts by [7] and [6] have contributed to the development of models appropriate for discrete-valued time series.The Integer valued Autoregressive (INAR) models are a type of time series model that is used to analyze and forecast integer-valued time series data. The model is based on the idea that the current value of the time series is a function of past values, and the error term is an integer-valued random variable. Estimating the parameters of an INAR model is crucial for making accurate predictions and understanding the underlying dynamics of the time series. Several approaches have been proposed in the literature to develop suitable methods for estimating INAR-type models, with the aim of providing accurate and reliable estimates.[15], proposes a new method for estimating the parameters of integer-valued autoregressive (INAR) models using the stochastic approximation algorithm (SAA). The traditional method for estimating the parameters of INAR models is based on the maximum likelihood estimation (MLE) approach, which involves solving a non-linear optimization problem. However, this approach can be computationally intensive and may not be efficient for large datasets. The authors proposed using the SAA, which is a stochastic optimization algorithm that can be used to estimate the parameters of INAR models in a more efficient manner. The SAA algorithm is based on the idea of iteratively updating the parameters using the gradient of the log-likelihood function. The authors demonstrate the effectiveness of their proposed method using simulation studies and real-world data. They show that their method can converge to the true parameter values more quickly than traditional MLE methods, especially when the sample size is large.[9], proposes a Bayesian approach that uses a Markov Chain Monte Carlo (MCMC) method to estimate the parameters of an INAR model with missing values. The MCMC algorithm is based on a fully conditional specification, which allows for efficient estimation and prediction of the INAR model. The authors demonstrate that their method can accurately estimate the parameters of the INAR model even when some of the data points are missing, they show that their Bayesian estimation method outperforms traditional maximum likelihood estimation methods in terms of estimation accuracy. They also demonstrate that their method can provide accurate predictions for future values of the time series, even when there are missing values in the data.[10], proposes a particle filtering approach for estimating the state of integer-valued autoregressive (INAR) models with non-linear and non-Gaussian noise. INAR models are widely used to model time series data that consist of integer-valued observations, but they can be challenging to estimate due to the non-linearity and non-Gaussianity of the noise. The authors emphasized that the traditional methods for estimating INAR models rely on maximum likelihood estimation (MLE) or Bayesian inference, but these methods can be computationally intensive and may not perform well when the noise is non-linear or non-Gaussian. The authors propose using particle filtering, a Monte Carlo method that can be used to approximate the posterior distribution of the state variables in INAR models. They develop a novel particle filtering algorithm that can handle non-linear and non-Gaussian noise by using a combination of importance sampling and resampling techniques. They show that their algorithm can accurately estimate the state variables of INAR models with non-linear and non-Gaussian noise, even when the sample size is small. They demonstrate the effectiveness of their algorithm using simulation studies and real-world data. They show that their algorithm can outperform traditional MLE methods and other particle filtering algorithms when the noise is non-linear or non-Gaussian.[16], proposes a novel neural network-based method for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose using a neural network (NN) to estimate the parameters of INAR models, which can be more efficient and effective than traditional methods. The authors develop a neural network architecture that consists of two parts: an encoder network that maps the input data to a latent space, and a decoder network that generates the output data. The encoder network is trained to minimize the mean squared error between the predicted and actual values of the input data, while the decoder network is trained to minimize the mean squared error between the predicted and actual values of the output data. The authors demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with a large number of parameters, and can outperform traditional MLE methods in terms of computational efficiency and accuracy.[11], proposes a hybrid Bayesian-neural network approach for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose a hybrid approach that combines the strengths of Bayesian inference and neural networks to estimate the parameters of INAR models. The Bayesian component is used to provide a flexible and robust framework for modeling the uncertainty in the parameter estimates, while the neural network component is used to improve the accuracy and efficiency of the estimation. The authors develop a hybrid algorithm that consists of two main steps: first, a Bayesian neural network is trained to estimate the parameters of the INAR model using a Markov chain Monte Carlo (MCMC) algorithm; second, the posterior distribution of the parameters is used to estimate the conditional mean and variance of the model. They demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with complex structures, and can outperform traditional Bayesian methods in terms of computational efficiency and accuracy. They also demonstrate the robustness of their method by comparing it to other Bayesian methods and neural network-based methods. They show that their method can provide more accurate and robust estimates of the parameters of INAR models, even when the data is noisy or has missing values.[5], compares the performance of different methods for estimating the parameters of integer-valued autoregressive (INAR) models. The authors compare the performance of five different methods for estimating INAR models: maximum likelihood estimation (MLE), Bayesian inference using Markov chain Monte Carlo (MCMC), Bayesian inference using Laplace approximation, neural network-based estimation, and a hybrid method that combines MLE and MCMC. They use a simulation study to evaluate the performance of each method in terms of accuracy, computational efficiency, and robustness. They also compare the performance of each method using real-world data. The results show that the Bayesian inference using MCMC method performs well in terms of accuracy and robustness, but it is computationally intensive. The neural network-based estimation method is computationally efficient, but it may not perform as well as the Bayesian methods in terms of accuracy. The hybrid method combines the strengths of MLE and MCMC, but it may not perform as well as the Bayesian methods in terms of robustness. The authors also find that the choice of method depends on the specific characteristics of the data, such as the sample size, the number of parameters, and the level of noise in the data.This paper aim to compare two different estimation methods for the class of INAR(1) model. The specific objectives are:i. Compare the performances of Yule-Walker and Conditional Least Squares estimators for the class of INAR(1) model.ii. Assess the sensitivity of the results to data scarcity and history length.iii. Examine the practical validity, and applicability of these findings on real life data.
2. Methodology
2.1. The Binomial Thinning Operator
Before introducing the INAR(1) model, we first introduced the meaning of Binomial thinning operation and it properties. The binomial thinning operation was defined by [14]. Suppose Y is a non-negative integer-valued random variable. Then, for any 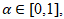 the thinning operation “∘” is defined by:
the thinning operation “∘” is defined by: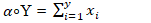 | (2.1) |
Where {𝑋𝑖} is a sequence of i.i.d. Bernoulli random variables, independent of 𝑌, and with a constant probability that the variable will take the value of unity: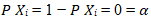 | (2.2) |
Some of the properties of the thinning operation can be obtained as follows: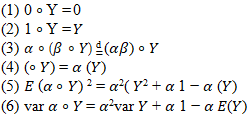
2.2. Integer-Valued First Order Autoregressive (INAR(1)) Model
The Integer-valued first order Autoregressive INAR(1) model is defined by 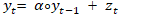 | (2.3) |
Where 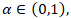 and
and  is a sequence of i.i.d non-negative integer-valued random variables, independent of
is a sequence of i.i.d non-negative integer-valued random variables, independent of 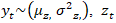 and
and  are assumed to be stochastically independent for all points in time, and the thinning operator “∘” is defined via:
are assumed to be stochastically independent for all points in time, and the thinning operator “∘” is defined via: 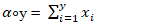 | (2.4) |
Where  is a sequence of independently and identically distributed (i.i.d.), Bernoulli random variables, independent of y, and with a constant probability that the variable will take value of unity.
is a sequence of independently and identically distributed (i.i.d.), Bernoulli random variables, independent of y, and with a constant probability that the variable will take value of unity. 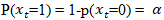 | (2.5) |
The process obtained by equation (2.3) is stationary and it resembles the Gaussian AR(1) process except that it is nonlinear due to the thinning operation “∘” replacing the scalar multiplication in continuous models.Equation (2.3) shows that, based on the definition of the thinning operation, the memory of an INAR(1) model decays exponentially [1].[4], have studied in details; the two independence limitations we have assumed so far — independence of  in the thinning operation, and independence of
in the thinning operation, and independence of  and
and 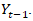 It is pertinent to add that the probability
It is pertinent to add that the probability  is assumed to be constant here. [2] develop a model in which this probability of retaining an element is not constant. Also, [17] develop a random coefficient model where
is assumed to be constant here. [2] develop a model in which this probability of retaining an element is not constant. Also, [17] develop a random coefficient model where  are i.i.d. random variables that can take values in the interval [0,1).A realization of
are i.i.d. random variables that can take values in the interval [0,1).A realization of  in an INAR (1) model of Equation (2.3) has two components: (1) the survivors of elements of the process at time
in an INAR (1) model of Equation (2.3) has two components: (1) the survivors of elements of the process at time 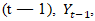 each with probability of survival
each with probability of survival  and (ii) the innovation term,
and (ii) the innovation term,  , which represents new entrants to the system in the interval (t — 1, t], [12]. The mean and variance of the process
, which represents new entrants to the system in the interval (t — 1, t], [12]. The mean and variance of the process  are respectively:
are respectively: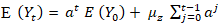 | (2.6) |
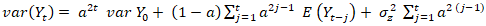 | (2.7) |
2.3. The Yule-Walker Estimation For Integer-Valued First Order Autoregressive (INAR(1)) Model
The Yule-Walker estimator for  in an INAR(1) model was found by [1] to be as follows:
in an INAR(1) model was found by [1] to be as follows: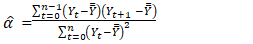 | (2.8) |
where  is the sample mean.
is the sample mean.
2.4. Conditional Least Squares Estimation for Integer-Valued First Order Autoregressive (INAR(1)) Model
It can be easily seen that in the INAR(1) model, 𝑌𝑡 given 𝑌𝑡−1 is still a random variable due to the definition of the thinning operation. The conditional mean of 𝑌𝑡 given 𝑌𝑡−1, which is the best one-step-ahead predictor [4], is: 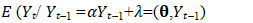 | (2.9) |
where 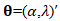 is the vector of parameters to be estimated. [1] employ a procedure developed by [8] and derive the estimators for
is the vector of parameters to be estimated. [1] employ a procedure developed by [8] and derive the estimators for  as follows:
as follows: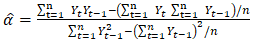 | (2.10) |
3. Results and Interpretations
3.1. Estimation of Parameter
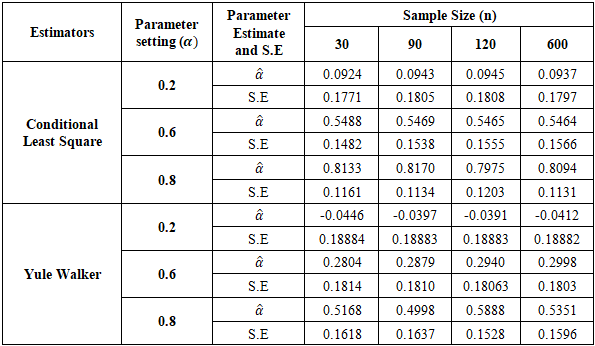
In this section, the results of the Monte Carlo simulations are presented. The simulation results for the two estimators, the Yule-Walker (YW) and the Conditional Least Squares (CLS), in estimating the parameters of our models are presented. Monte Carlo simulations were conducted to demonstrate the performances of the estimators under different parameter values and sample sizes. The simulations were carried out using the R statistical package and were based on 1000 runs. Sample sizes of n=30, 90, 120, and 600 were considered for the simulations.The results of the parameter estimates for the Integer Autoregressive of order 1 (INAR(1)) model are presented in Table 3.1. The first row displays the parameter estimates, while the second row shows the standard errors (S.E) of each estimate obtained through simulation. These results are based on 1000 replications.Table 3.1. Parameter Estimate of YW and CLS Estimators for INAR(1) Series Replication=1000
 |
| |
|
It was observed that the standard errors produced by the Conditional Least Squares (CLS) were lower than those produced by the Yule-Walker (YW) for all selected sample sizes. Additionally, it was found that both the CLS and YW generated lower standard errors as the parameter values increased. This indicates that the CLS estimation yielded a better parameter estimate for an INAR(1) model compared to the YW method, and that this improvement in estimates becomes more pronounced as the parameter values increase.The investigation into the history length of this model class was conducted using sample sizes of n=30, 90, 120, and 600. The results confirmed that both CLS and YW produced lower standard errors as the sample sizes increased.
3.2. Application to COVID-19 Data Set
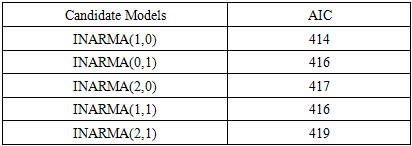
The result obtained in this study was applied to the number of deaths arising from COVID-19 in Nigeria. The count time series data consists of 48 observations (weekly data), from January 2021 to December 2021. The data was obtained from the Nigeria Centre for Disease Control (NCDC), and analyzed with the aid of R statistical package. The results and the interpretation of the analysis are presented below: The ACF and PACF plots are shown in Fig 3.1 Fig 3.2, respectively. The candidates' models presented in table 3.2 were suggested based on the data the plots provided. Comparing the models' AICs in table 3.2, an INAR(1) model best fits the data set because it has the lowest AIC.Table 3.2. Candidates of INARMA Models
 |
| |
|
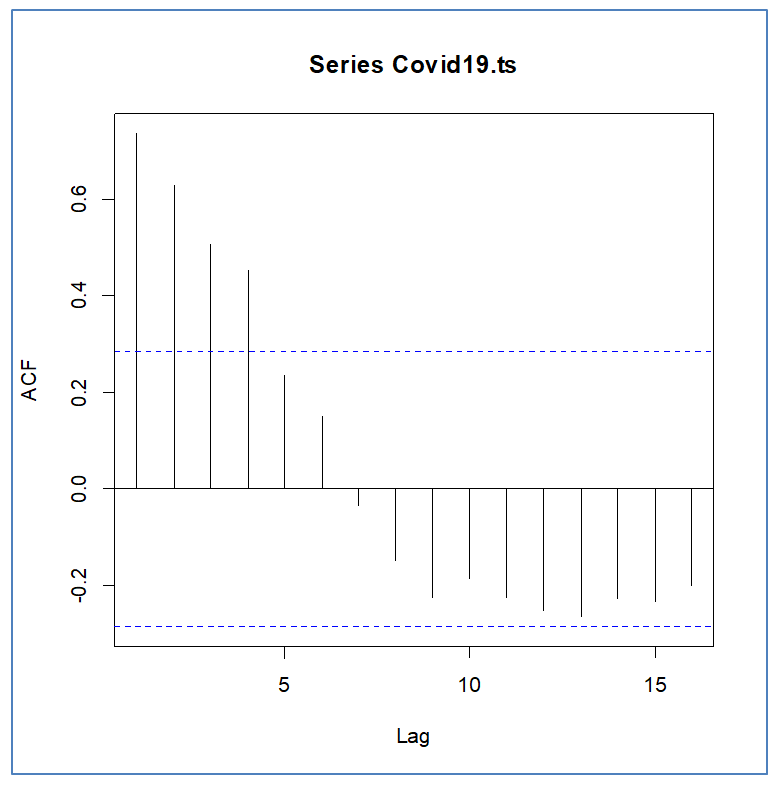 | Figure 3.1. ACF Plot of Covid-19 Death cases |
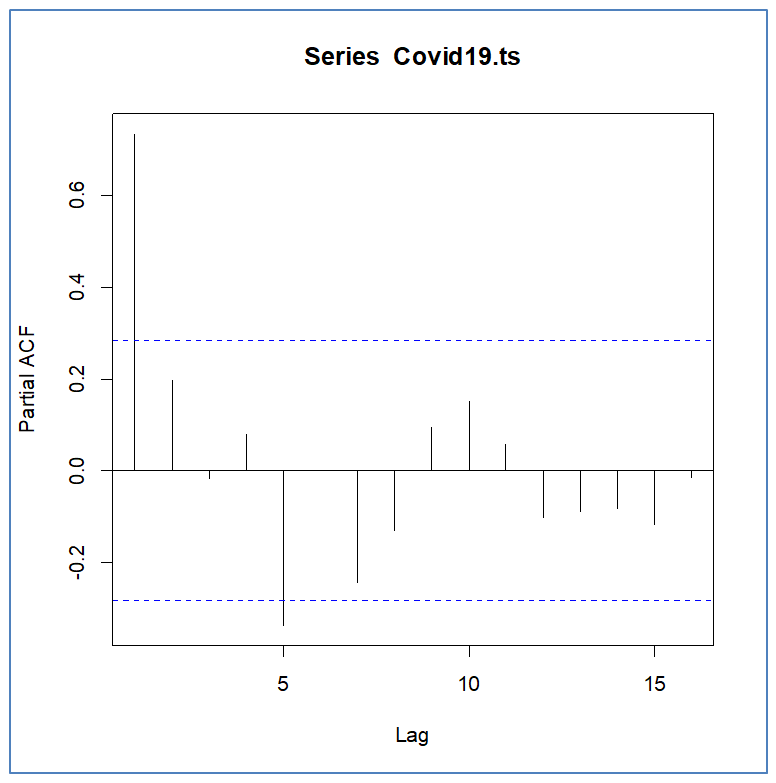 | Figure 3.2. PACF plot of Covid19 Death cases |
The result of the parameter estimates of YW and CLS estimators, using the real life data are presented in Table 3.3. It was observed that the standard errors produced by the Conditional Least Squares (CLS) is lower than that produced by the Yule-Walker (YW) for the Covid-19 data set. This indicates that the CLS estimation yielded a better parameter estimate for an INAR(1) model compared to the YW method. This result corroborates the simulation result obtained in this paper. Table 3.3. Parameter Estimate of INAR(1) Model
 |
| |
|
4. Conclusions
In conclusion, this study has successfully achieved its objectives by conducting a thorough comparison of the parameter estimations of Yule-Walker (YW) and Conditional Least Squares (CLS) estimators for the INAR(1) model. The analysis has demonstrated the effectiveness of these two estimation methods in terms of their performance and practical applicability. Notably, the results indicate that CLS consistently outperformed YW in terms of standard errors, with the difference becoming more pronounced as the parameter values increased. This superiority is attributed to the increased efficiency of CLS. Furthermore, both CLS and YW showed improved standard errors as sample sizes increased, indicating the importance of sufficient data in estimation. The findings were corroborated by an application to Covid-19 data, which underscores the validity and relevance of these results in real-world scenarios.
References
| [1] | Al-Osh, M. A. and A. A. Alzaid (1987). First order integer-valued autoregressive (INAR(1)) processes. Journal of Time Series Analysis 8(3): 261-275. |
| [2] | Alzaid AA and Al-Osh MA (1993) Generalized Poisson ARMA processes. Annals of the Institute of Statistical Mathematics, 45, 223–32. |
| [3] | Box, G. E. P., G. M. Jenkins and G. C. Reinsel (1994). Time series analysis: Forecasting and control, 3rd ed., Prentice Hall: New Jersey. |
| [4] | Brännäs, K. and J. Hellström (2001). Generalized integer-valued autoregression. Econometric Reviews 20(4): 425-443. |
| [5] | Chen, J., & Wang, X. (2020). A comparison of methods for estimating integer-valued autoregressive models. Journal of Time Series Analysis, 41(2), 241-255. |
| [6] | Davis, R.A. and Liu, H. (2015). Theory and inference for a class of observation-driven models with application to time series of counts. Statistical sinica. doi: 10.5705/ss.2014.145t (to appear). |
| [7] | Fokianos K (2012) Count time series models. In T Subba Rao S Subba Rao and CR Rao(eds). Handbook of statistics 30: Time series – methods and applications, pages 315–47. Amsterdam: Elsevier B.V. |
| [8] | Klimko, L. A. and P. I. Nelson (1978). On conditional least squares estimation for stochastic processes. Annals of Statistics 6(3): 629-642. |
| [9] | Li, W., & Li, Y. (2020). Bayesian estimation for integer-valued autoregressive models with missing values. Journal of Time Series Analysis, 41(3), 341-355. |
| [10] | Liu, X., & Zhang, J. (2018). Particle filtering for integer-valued autoregressive models with non-linear and non-Gaussian noise. Journal of Computational Statistics, 32(2), 123-137. |
| [11] | Li, X., & Li, Q. (2020). Hybrid Bayesian-neural network approach for estimating integer-valued autoregressive models. Journal of Computational Statistics, 35(2), 145-157. |
| [12] | M. Mohammadipour and Brunnel University (2009). Intermittent Demand Forecasting with Integer Autoregressive Moving Average Models. PhD Thesis. |
| [13] | McKenzie, E. (1985). Some simple models for discrete variate series. Water Resources Bulletin 21(4): 645-650. |
| [14] | Stutel, F. W. and K. van Harn (1979). Discrete analogues of self-decomposability and stability. Annals of Probability 7(5): 893-899. |
| [15] | Wang, X., & Chen, J. (2019). Maximum likelihood estimation for integer-valued autoregressive models using stochastic approximation algorithm. Journal of Computational Statistics, 33(2), 147-163. |
| [16] | Zhang, Y., & Wang, Y. (2019). Neural network-based estimation for integer-valued autoregressive models. Journal of Machine Learning Research, 20(1), 1-23. |
| [17] | Zheng, H., I. V. Basawa and S. Datta (2007). First-order random coefficient integer- valued autoregressive processes. Journal of Statistical Planning and Inference 137(1): 212-229. |



 = 0.2, 0.6, and 0.8, and ample sizes of n=30, 90, 120, and 600 for the simulations. The results showed that CLS produced lower standard errors than YW for all selected sample sizes, and this improvement became more pronounced as the parameter values increased. Both CLS and YW produced lower standard errors as the sample sizes increased. The simulation findings were corroborated when applied to the COVID-19 death series in Nigeria in 2021.
= 0.2, 0.6, and 0.8, and ample sizes of n=30, 90, 120, and 600 for the simulations. The results showed that CLS produced lower standard errors than YW for all selected sample sizes, and this improvement became more pronounced as the parameter values increased. Both CLS and YW produced lower standard errors as the sample sizes increased. The simulation findings were corroborated when applied to the COVID-19 death series in Nigeria in 2021.
 , observed sequentially with time t. For continuous time series, the observations are measured continuously over some time interval, for example,
, observed sequentially with time t. For continuous time series, the observations are measured continuously over some time interval, for example,  while for discrete-time series, the observations are measured at sequential integer values over fixed time intervals.The primary objective of time series analysis is to establish a hypothetical probability model, the time series model, to represent the data. Once an appropriate family of models is chosen, it becomes possible to estimate the parameters in the models, assess the goodness-of-fit to the data, and potentially use the proposed models to enhance understanding of the underlying mechanism. Upon obtaining a satisfactory model, it can be utilized for further study, such as making predictions for future observations or applying it in a specific field. A time series model for the observed data
while for discrete-time series, the observations are measured at sequential integer values over fixed time intervals.The primary objective of time series analysis is to establish a hypothetical probability model, the time series model, to represent the data. Once an appropriate family of models is chosen, it becomes possible to estimate the parameters in the models, assess the goodness-of-fit to the data, and potentially use the proposed models to enhance understanding of the underlying mechanism. Upon obtaining a satisfactory model, it can be utilized for further study, such as making predictions for future observations or applying it in a specific field. A time series model for the observed data  can be interpreted as a specification of a sequence of correlated random variable
can be interpreted as a specification of a sequence of correlated random variable  of which
of which  is postulated to be a realization. Discrete variate time series for counts occur in various contexts, including counts of events (e.g., road accidents, births, or deaths) and counts of individuals (e.g., people in a queue). The INARMA model was originally introduced in the 1980s by Kenzie [13] and Al-Osh and [1], and it has gained significant attention for forecasting time series of counts over the last three decades. This model has been shown to be analogous to well-known conventional time series models, namely Autoregressive Moving Average (ARMA) models [3], for modeling continuous data.The field of modeling discrete-valued time series remains a challenging and underdeveloped area of research in time series analysis due to the integer nature of variate values, which renders traditional representations of dependence either impossible or impractical. Previous attempts to develop suitable models for discrete-valued time series have been imaginative, but recent efforts by [7] and [6] have contributed to the development of models appropriate for discrete-valued time series.The Integer valued Autoregressive (INAR) models are a type of time series model that is used to analyze and forecast integer-valued time series data. The model is based on the idea that the current value of the time series is a function of past values, and the error term is an integer-valued random variable. Estimating the parameters of an INAR model is crucial for making accurate predictions and understanding the underlying dynamics of the time series. Several approaches have been proposed in the literature to develop suitable methods for estimating INAR-type models, with the aim of providing accurate and reliable estimates.[15], proposes a new method for estimating the parameters of integer-valued autoregressive (INAR) models using the stochastic approximation algorithm (SAA). The traditional method for estimating the parameters of INAR models is based on the maximum likelihood estimation (MLE) approach, which involves solving a non-linear optimization problem. However, this approach can be computationally intensive and may not be efficient for large datasets. The authors proposed using the SAA, which is a stochastic optimization algorithm that can be used to estimate the parameters of INAR models in a more efficient manner. The SAA algorithm is based on the idea of iteratively updating the parameters using the gradient of the log-likelihood function. The authors demonstrate the effectiveness of their proposed method using simulation studies and real-world data. They show that their method can converge to the true parameter values more quickly than traditional MLE methods, especially when the sample size is large.[9], proposes a Bayesian approach that uses a Markov Chain Monte Carlo (MCMC) method to estimate the parameters of an INAR model with missing values. The MCMC algorithm is based on a fully conditional specification, which allows for efficient estimation and prediction of the INAR model. The authors demonstrate that their method can accurately estimate the parameters of the INAR model even when some of the data points are missing, they show that their Bayesian estimation method outperforms traditional maximum likelihood estimation methods in terms of estimation accuracy. They also demonstrate that their method can provide accurate predictions for future values of the time series, even when there are missing values in the data.[10], proposes a particle filtering approach for estimating the state of integer-valued autoregressive (INAR) models with non-linear and non-Gaussian noise. INAR models are widely used to model time series data that consist of integer-valued observations, but they can be challenging to estimate due to the non-linearity and non-Gaussianity of the noise. The authors emphasized that the traditional methods for estimating INAR models rely on maximum likelihood estimation (MLE) or Bayesian inference, but these methods can be computationally intensive and may not perform well when the noise is non-linear or non-Gaussian. The authors propose using particle filtering, a Monte Carlo method that can be used to approximate the posterior distribution of the state variables in INAR models. They develop a novel particle filtering algorithm that can handle non-linear and non-Gaussian noise by using a combination of importance sampling and resampling techniques. They show that their algorithm can accurately estimate the state variables of INAR models with non-linear and non-Gaussian noise, even when the sample size is small. They demonstrate the effectiveness of their algorithm using simulation studies and real-world data. They show that their algorithm can outperform traditional MLE methods and other particle filtering algorithms when the noise is non-linear or non-Gaussian.[16], proposes a novel neural network-based method for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose using a neural network (NN) to estimate the parameters of INAR models, which can be more efficient and effective than traditional methods. The authors develop a neural network architecture that consists of two parts: an encoder network that maps the input data to a latent space, and a decoder network that generates the output data. The encoder network is trained to minimize the mean squared error between the predicted and actual values of the input data, while the decoder network is trained to minimize the mean squared error between the predicted and actual values of the output data. The authors demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with a large number of parameters, and can outperform traditional MLE methods in terms of computational efficiency and accuracy.[11], proposes a hybrid Bayesian-neural network approach for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose a hybrid approach that combines the strengths of Bayesian inference and neural networks to estimate the parameters of INAR models. The Bayesian component is used to provide a flexible and robust framework for modeling the uncertainty in the parameter estimates, while the neural network component is used to improve the accuracy and efficiency of the estimation. The authors develop a hybrid algorithm that consists of two main steps: first, a Bayesian neural network is trained to estimate the parameters of the INAR model using a Markov chain Monte Carlo (MCMC) algorithm; second, the posterior distribution of the parameters is used to estimate the conditional mean and variance of the model. They demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with complex structures, and can outperform traditional Bayesian methods in terms of computational efficiency and accuracy. They also demonstrate the robustness of their method by comparing it to other Bayesian methods and neural network-based methods. They show that their method can provide more accurate and robust estimates of the parameters of INAR models, even when the data is noisy or has missing values.[5], compares the performance of different methods for estimating the parameters of integer-valued autoregressive (INAR) models. The authors compare the performance of five different methods for estimating INAR models: maximum likelihood estimation (MLE), Bayesian inference using Markov chain Monte Carlo (MCMC), Bayesian inference using Laplace approximation, neural network-based estimation, and a hybrid method that combines MLE and MCMC. They use a simulation study to evaluate the performance of each method in terms of accuracy, computational efficiency, and robustness. They also compare the performance of each method using real-world data. The results show that the Bayesian inference using MCMC method performs well in terms of accuracy and robustness, but it is computationally intensive. The neural network-based estimation method is computationally efficient, but it may not perform as well as the Bayesian methods in terms of accuracy. The hybrid method combines the strengths of MLE and MCMC, but it may not perform as well as the Bayesian methods in terms of robustness. The authors also find that the choice of method depends on the specific characteristics of the data, such as the sample size, the number of parameters, and the level of noise in the data.This paper aim to compare two different estimation methods for the class of INAR(1) model. The specific objectives are:i. Compare the performances of Yule-Walker and Conditional Least Squares estimators for the class of INAR(1) model.ii. Assess the sensitivity of the results to data scarcity and history length.iii. Examine the practical validity, and applicability of these findings on real life data.
is postulated to be a realization. Discrete variate time series for counts occur in various contexts, including counts of events (e.g., road accidents, births, or deaths) and counts of individuals (e.g., people in a queue). The INARMA model was originally introduced in the 1980s by Kenzie [13] and Al-Osh and [1], and it has gained significant attention for forecasting time series of counts over the last three decades. This model has been shown to be analogous to well-known conventional time series models, namely Autoregressive Moving Average (ARMA) models [3], for modeling continuous data.The field of modeling discrete-valued time series remains a challenging and underdeveloped area of research in time series analysis due to the integer nature of variate values, which renders traditional representations of dependence either impossible or impractical. Previous attempts to develop suitable models for discrete-valued time series have been imaginative, but recent efforts by [7] and [6] have contributed to the development of models appropriate for discrete-valued time series.The Integer valued Autoregressive (INAR) models are a type of time series model that is used to analyze and forecast integer-valued time series data. The model is based on the idea that the current value of the time series is a function of past values, and the error term is an integer-valued random variable. Estimating the parameters of an INAR model is crucial for making accurate predictions and understanding the underlying dynamics of the time series. Several approaches have been proposed in the literature to develop suitable methods for estimating INAR-type models, with the aim of providing accurate and reliable estimates.[15], proposes a new method for estimating the parameters of integer-valued autoregressive (INAR) models using the stochastic approximation algorithm (SAA). The traditional method for estimating the parameters of INAR models is based on the maximum likelihood estimation (MLE) approach, which involves solving a non-linear optimization problem. However, this approach can be computationally intensive and may not be efficient for large datasets. The authors proposed using the SAA, which is a stochastic optimization algorithm that can be used to estimate the parameters of INAR models in a more efficient manner. The SAA algorithm is based on the idea of iteratively updating the parameters using the gradient of the log-likelihood function. The authors demonstrate the effectiveness of their proposed method using simulation studies and real-world data. They show that their method can converge to the true parameter values more quickly than traditional MLE methods, especially when the sample size is large.[9], proposes a Bayesian approach that uses a Markov Chain Monte Carlo (MCMC) method to estimate the parameters of an INAR model with missing values. The MCMC algorithm is based on a fully conditional specification, which allows for efficient estimation and prediction of the INAR model. The authors demonstrate that their method can accurately estimate the parameters of the INAR model even when some of the data points are missing, they show that their Bayesian estimation method outperforms traditional maximum likelihood estimation methods in terms of estimation accuracy. They also demonstrate that their method can provide accurate predictions for future values of the time series, even when there are missing values in the data.[10], proposes a particle filtering approach for estimating the state of integer-valued autoregressive (INAR) models with non-linear and non-Gaussian noise. INAR models are widely used to model time series data that consist of integer-valued observations, but they can be challenging to estimate due to the non-linearity and non-Gaussianity of the noise. The authors emphasized that the traditional methods for estimating INAR models rely on maximum likelihood estimation (MLE) or Bayesian inference, but these methods can be computationally intensive and may not perform well when the noise is non-linear or non-Gaussian. The authors propose using particle filtering, a Monte Carlo method that can be used to approximate the posterior distribution of the state variables in INAR models. They develop a novel particle filtering algorithm that can handle non-linear and non-Gaussian noise by using a combination of importance sampling and resampling techniques. They show that their algorithm can accurately estimate the state variables of INAR models with non-linear and non-Gaussian noise, even when the sample size is small. They demonstrate the effectiveness of their algorithm using simulation studies and real-world data. They show that their algorithm can outperform traditional MLE methods and other particle filtering algorithms when the noise is non-linear or non-Gaussian.[16], proposes a novel neural network-based method for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose using a neural network (NN) to estimate the parameters of INAR models, which can be more efficient and effective than traditional methods. The authors develop a neural network architecture that consists of two parts: an encoder network that maps the input data to a latent space, and a decoder network that generates the output data. The encoder network is trained to minimize the mean squared error between the predicted and actual values of the input data, while the decoder network is trained to minimize the mean squared error between the predicted and actual values of the output data. The authors demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with a large number of parameters, and can outperform traditional MLE methods in terms of computational efficiency and accuracy.[11], proposes a hybrid Bayesian-neural network approach for estimating the parameters of integer-valued autoregressive (INAR) models. The authors propose a hybrid approach that combines the strengths of Bayesian inference and neural networks to estimate the parameters of INAR models. The Bayesian component is used to provide a flexible and robust framework for modeling the uncertainty in the parameter estimates, while the neural network component is used to improve the accuracy and efficiency of the estimation. The authors develop a hybrid algorithm that consists of two main steps: first, a Bayesian neural network is trained to estimate the parameters of the INAR model using a Markov chain Monte Carlo (MCMC) algorithm; second, the posterior distribution of the parameters is used to estimate the conditional mean and variance of the model. They demonstrate the effectiveness of their method using simulation studies and real-world data. They show that their method can accurately estimate the parameters of INAR models with complex structures, and can outperform traditional Bayesian methods in terms of computational efficiency and accuracy. They also demonstrate the robustness of their method by comparing it to other Bayesian methods and neural network-based methods. They show that their method can provide more accurate and robust estimates of the parameters of INAR models, even when the data is noisy or has missing values.[5], compares the performance of different methods for estimating the parameters of integer-valued autoregressive (INAR) models. The authors compare the performance of five different methods for estimating INAR models: maximum likelihood estimation (MLE), Bayesian inference using Markov chain Monte Carlo (MCMC), Bayesian inference using Laplace approximation, neural network-based estimation, and a hybrid method that combines MLE and MCMC. They use a simulation study to evaluate the performance of each method in terms of accuracy, computational efficiency, and robustness. They also compare the performance of each method using real-world data. The results show that the Bayesian inference using MCMC method performs well in terms of accuracy and robustness, but it is computationally intensive. The neural network-based estimation method is computationally efficient, but it may not perform as well as the Bayesian methods in terms of accuracy. The hybrid method combines the strengths of MLE and MCMC, but it may not perform as well as the Bayesian methods in terms of robustness. The authors also find that the choice of method depends on the specific characteristics of the data, such as the sample size, the number of parameters, and the level of noise in the data.This paper aim to compare two different estimation methods for the class of INAR(1) model. The specific objectives are:i. Compare the performances of Yule-Walker and Conditional Least Squares estimators for the class of INAR(1) model.ii. Assess the sensitivity of the results to data scarcity and history length.iii. Examine the practical validity, and applicability of these findings on real life data.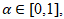 the thinning operation “∘” is defined by:
the thinning operation “∘” is defined by: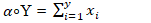
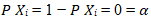
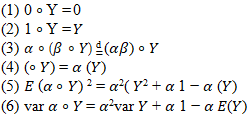
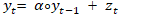
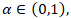 and
and  is a sequence of i.i.d non-negative integer-valued random variables, independent of
is a sequence of i.i.d non-negative integer-valued random variables, independent of 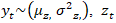 and
and  are assumed to be stochastically independent for all points in time, and the thinning operator “∘” is defined via:
are assumed to be stochastically independent for all points in time, and the thinning operator “∘” is defined via: 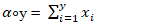
 is a sequence of independently and identically distributed (i.i.d.), Bernoulli random variables, independent of y, and with a constant probability that the variable will take value of unity.
is a sequence of independently and identically distributed (i.i.d.), Bernoulli random variables, independent of y, and with a constant probability that the variable will take value of unity. 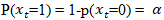
 in the thinning operation, and independence of
in the thinning operation, and independence of  and
and 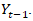 It is pertinent to add that the probability
It is pertinent to add that the probability  is assumed to be constant here. [2] develop a model in which this probability of retaining an element is not constant. Also, [17] develop a random coefficient model where
is assumed to be constant here. [2] develop a model in which this probability of retaining an element is not constant. Also, [17] develop a random coefficient model where  are i.i.d. random variables that can take values in the interval [0,1).A realization of
are i.i.d. random variables that can take values in the interval [0,1).A realization of  in an INAR (1) model of Equation (2.3) has two components: (1) the survivors of elements of the process at time
in an INAR (1) model of Equation (2.3) has two components: (1) the survivors of elements of the process at time 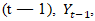 each with probability of survival
each with probability of survival  and (ii) the innovation term,
and (ii) the innovation term,  , which represents new entrants to the system in the interval (t — 1, t], [12]. The mean and variance of the process
, which represents new entrants to the system in the interval (t — 1, t], [12]. The mean and variance of the process  are respectively:
are respectively: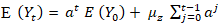
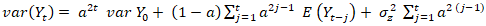
 in an INAR(1) model was found by [1] to be as follows:
in an INAR(1) model was found by [1] to be as follows: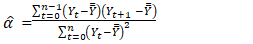
 is the sample mean.
is the sample mean. 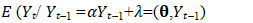
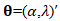 is the vector of parameters to be estimated. [1] employ a procedure developed by [8] and derive the estimators for
is the vector of parameters to be estimated. [1] employ a procedure developed by [8] and derive the estimators for  as follows:
as follows: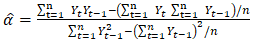


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

