1. Introduction

Several studies have shown that creating ensembles of base learners can significantly improve learning performance. Boosting [1], random forests [2], bagging [3], and their variations are among the most commonly utilized examples of this approach. When it comes to classification and regression, boosting and random forests are comparable and sometimes even outperform, state-of-the-art techniques [4]. The margin and correlation of base classifiers are typically used to describe the effectiveness of ensemble approaches [5]. Base classifiers must be accurate and diversified, meaning they should predict differently, to have a decent ensemble. The ensemble's extremely accurate predictions are then guaranteed by the voting mechanism that runs on the top of the base learners. It is important to have a variety of decision-makers in the "committee" of basic models to make better decisions. This diversity, referred to as the base learners' "diversity," is essential as there will be no progress from a collection of similar models. Ensemble models that perform well individually and collectively have been shown to exhibit diversity in base learners. Techniques like bagging, random forests, and boosting algorithms have been utilized to add variety to ensemble models.

In the bagging method described in [3], N samples are considered, replacing the training data to produce N training data sets. Each of these sets is used to build a learning algorithm, usually a decision tree. The final prediction is made by averaging or voting on the class label. Bagging introduces random discrepancies between the input data sets to add variety to the ensemble model. The random forest learning method [6] adds further variability to the bagging process. To reduce the interconnection among the constructed trees, the random forest method chooses a random set of features each time, while also using replacement to generate N training datasets. The result is again an average or a collective vote based on all predictions made by the forest’s-built trees (Fig. 1).

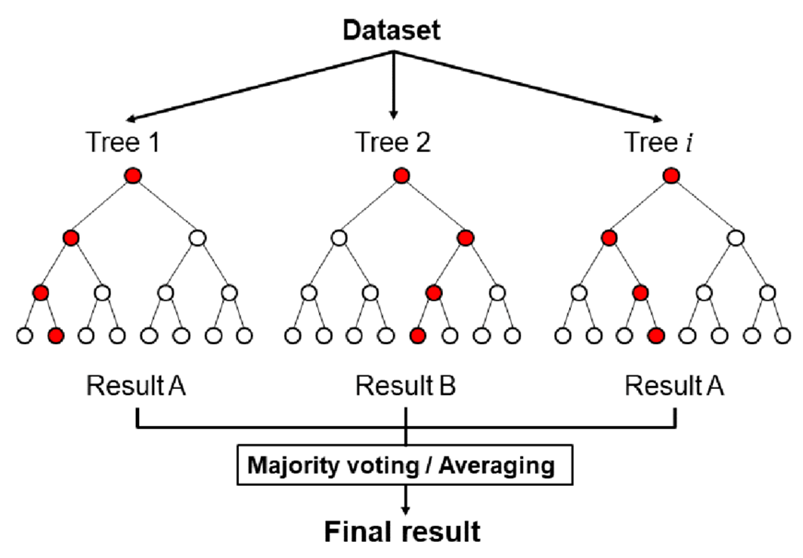Figure 1. Random forest classifier uses majority voting of the predictions made by randomly created decision trees to make the final predictions

Random forests are commonly used in various applications and have shown impressive performance. However, making minor adjustments in how the base learners are combined could enhance the predictions even more. Using a simple average for the final predictions, assuming that all base learners have equal weights, may seem illogical. The reason for randomizing input feature selection and sampling is to ensure that every constructed tree is not capable of making the same decisions [7]. Therefore, implementing a weighting process to weigh the trees based on their performance seems fair.

[7] proposed tree-weighted random forest (TWRF) method for classifying high dimensional noisy data. They contended that a new approach for ranking the trees based on their classification capability could serve as a solution for random forests, which are affected by noisy data and susceptible to making inaccurate decisions. By assessing the trees in the forest using an out-of-bag (OOB) subset of the training data, they calculated the tree weights based on the OOB accuracies. The results demonstrated that TWRF outperformed the regular random forest.

Various studies have proposed changes to the weighted random forest, and have demonstrated slight improvements in their results compared to traditional random forest predictions [8]. For instance, [9] examined some adjustments to enhance the performance of the random forest algorithm. Instead of using the Gini index for evaluation, the author combined five attributes evaluation measures. Additionally, the article identified the most similar examples to the target instance and suggested a weighted random forest with weights based on the vote margins of these similar instances. Numerical results on various datasets showed the effectiveness of the proposed method in improving performance.

In a separate study, [10] proposed a probabilistic weighted system for combining forest trees, considering four combination methods: recall combiner, majority vote, weighted majority vote, and naive Bayes combiner. The weighted majority vote is a preferable weighting approach for small unbalanced data sets, while the naïve Bayes combiner is somewhat superior to other options, particularly for large balanced data sets based on experimental results with 73 data sets.

In this study, we propose optimization and stacking-based weighting mechanisms to combine the trees of the forest more effectively. For integrating the benefits of the model combinations having diverse input models is a key. To achieve this, we aim to keep the trees of the forest shallow to prevent near-identical, non-diverse trees as input features. The designed models include optimal weighted random forest based on accuracy, optimal weighted random forest based on area under the curve (AUC), and several stacking-based weighted random forest models.

2. Material and Methods

A diverse set of initial base learners is necessary to improve the performance of the ensemble model. This means that there should be little association between the base models. Thus, the ensemble random forest models are designed with the assumption that the trees in the forest should be constructed shallow, meaning they should not have large depths. This results in a reasonable degree of variation amongst the base decision trees. The improved designed weighted random forest models are explained below.

2.1. Random Forest

Breiman [2] employed random forests, which are made up of an ensemble of K classifiers, h₁(x), h₂(x),..., h_k(x). A winning class is assigned to an instance that is being classed, with each classifier casting a vote for one of the classes. The combined classifier is represented by h(x). A replacement is chosen at random from the training set of n instances for each training set of n instances. By using a sampling technique known as bootstrap replication, each tree is constructed with an average of 36.8% fewer training instances. These "out-of-bag" examples are useful when estimating the strength and correlation of the forest internally.

For classifier h_k, denote the set of out-of-bag instances as O_k. Let Q(x, y_j) represent the out-of-bag percentage of votes for class y_j at input x and P(h(x) = y_j) be an estimation.

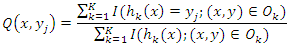The indicator function is denoted by I(·). The margin function calculates the difference between the average vote in class y and the average vote in any other class:

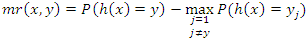It is estimated with Q(x,y) and Q(x,y_j). Strength is defined as the expected margin, and is computed as the average over the training set:

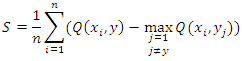The average correlation is computed as the variance of the margin over the square of standard deviation of the forest: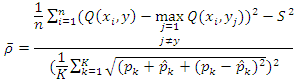

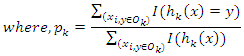is an out-of-bag estimate of P(h_k(x) = y) and

Where

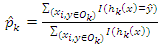is an out-of-bag estimate of 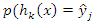and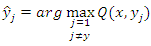

is estimated for every instance x in the training set with Q(x, y_j).

2.2. Accuracy-Based Optimal Weighted Random Forest

The motivation for creating an optimal weighted random forest is based on the optimization model suggested in [11], which aimed to minimize the mean squared error (MSE) of a linear combination of multiple base regressors. In this context, we present an optimization model to minimize the prediction accuracy of a weighted random forest ensemble model for binary classification, with the weights serving as decision variables. The out-of-bag predictions produced by k-fold cross-validation are treated as substitutes for unseen test observations and are utilized as inputs for the optimization problem. The following is the mathematical model.

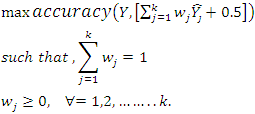(1)

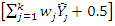Where Y represents the vector of actual response values, Y_j is the out-of-bag prediction of decision tree j, and w_j are the weights corresponding to decision tree j (j = 1,.., k). The accuracy() function measures the percentage of accurate predictions (true positives and true negatives) among all examples investigated. In addition, for the ensemble model, finds the closest integer between class labels (0 and 1). (see Fig. 2).

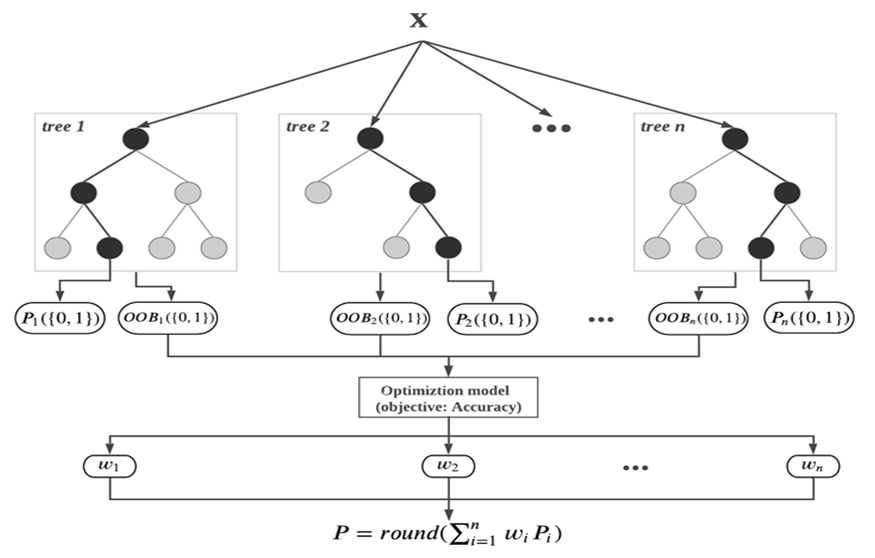Figure 2. The optimal weighted random forest classifier utilizes out-of-bag (OOB) binary predictions from the randomly generated decision trees to enhance prediction accuracy

2.3. Area under the Curve (AUC)-Based Optimal Weighted Random Forest

The AUC (Area under the ROC curve) is a metric primarily used to compare various classifiers. The ROC curve is a commonly used graph that illustrates the balance between true positive and false positive rates at different thresholds for classification. The AUC, which represents the area under this curve, is valuable for comparing binary classifiers as it considers all potential thresholds. Furthermore, accuracy has a built-in limitation of reporting excessively high accuracy when classifying highly imbalanced data sets [12,21]. The optimization model below aims to determine the best weights for combining trees in a random forest model by optimizing the ensemble's AUC.

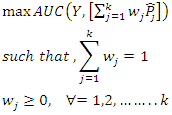(2)

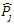The out-of-bag probability vector of each base classifier is referred to as in the previous formulation, and the area under the ROC curve for the created ensemble is calculated by AUC().

2.4. Random Forest Model Based on Stacking

Random forest models with stacking involve combining multiple base learners to complete at least one additional level of the learning activity. The independent and dependent variables of the second-level learning problem are the actual response values of the training data and the out-of-bag predictions of the base learners [13]. Here, we used these steps to utilize the out-of-bag predictions from the forest's trees and train another machine learning model on top of them to create an enhanced random forest.

i. Build a random forest model using the training data.

ii. Using 𝑘-fold cross-validation to obtain the forest's decision trees and generate out-of-bag predictions for each tree.

iii. Create a new dataset with the response variable as the actual response values of the training data points and the input variables as the out-of-bag predictions.

iv. Train a second-level machine learning model using the generated dataset to predict test observations that have not been seen before.

As the second-level classifier, we have selected three machine learning models: logistic regression, K-nearest neighbors, and random forest. Additionally, for each second-level classifier, two scenarios are considered: either using out-of-bag predictions of the probability that an observation belongs to the majority class or using binary classifications of those predictions. In the second scenario, the probability of the actual class (class 1) is used as the input variable instead of binary predictions.

3. Experiments and Results

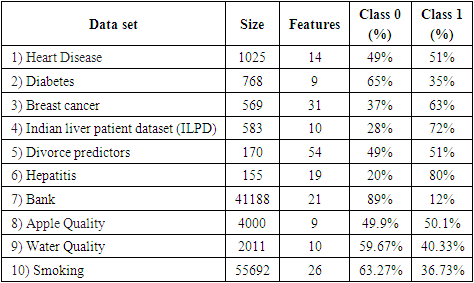
Ten public binary classification datasets from the UCI machine learning repository [14] were utilized to evaluate the effectiveness of the proposed enhanced weighted random forest classifiers. Minimal pre-processing work, such as handling missing values and one hot encoding, was conducted to prepare each dataset for training classification models. Twenty percent of each dataset was reserved as the test set to evaluate the actual performance of the models created, while the remaining eighty percent was used to build and optimize the ensemble.

The number of trees (𝑛) is set at 100 to train the regular random forest and generate 𝑛 randomly created decision trees. The maximum depth of the trees is set at half of the common choice for the maximum depth of random forest trees, which is the square root of the number of features (√𝑝 ⁄ 2). This keeps the trees shallow and uncorrelated with one another. Ten-fold cross-validation is used to create decision tree out-of-bag predictions. The Sequential Least Squares Programming technique (SLSQP) from Python's SciPy optimization module was used to solve the optimization problems [15].

Table 1 displays the dimensions, number of features, and percentage of class labels for 10 sample data sets that were taken from the UCI machine learning repository. This table shows that varying sizes and percentage of class labels are covered by the selected data sets.

Table 1. Details of example data sets downloaded from UCI machine learning repository

Table 2 shows the complete experimental results of all ensemble models created and used on the sample datasets. Two methods have been developed for stacking-based ensembles: binary OOB predictions and OOB probability forecasts of the true class label. The results indicate that at least one of the proposed models outperforms the standard random forest in 8 out of the 10 data sets considered (first column of the table). Moreover, it seems that the stacking-based random forest, with a second random forest model as the second-level classifier, outperforms other models more frequently based on binary OOB predictions (based on 10 data sets).

Table 2. Results of experiments comparing regular random forest classifiers to build improved random forest classifiers. For every data set, the top-performing classifier is highlighted. The last row displays the average accuracy of every model while taking into account every data set

Figure 3 depicts the mean accuracy of the models created across all datasets in an effort to compare the performance of the suggested upgraded random forest classifiers with conventional random forests more effectively. This figure represents a comparison of the average accuracy scores of all models using a standard random forest classifier. The graph clearly indicates that RF stacked RF using binary OOB predictions outperforms regular random forest. This classifier has the potential to enhance predictions made by ordinary random forests by 0.13%.

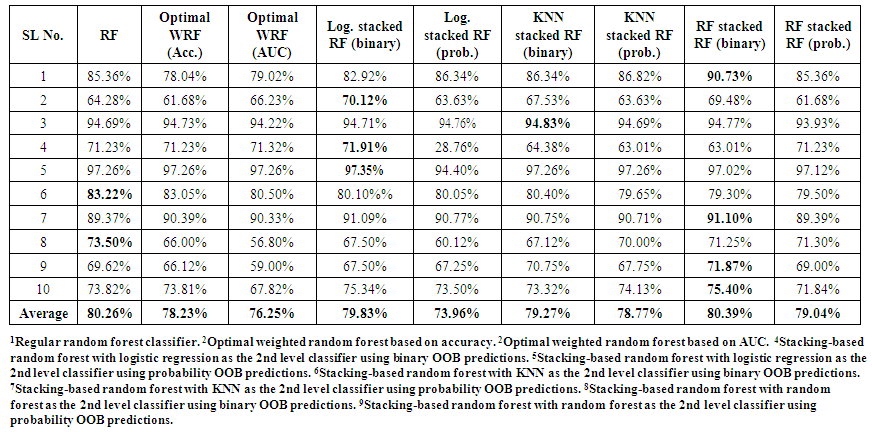
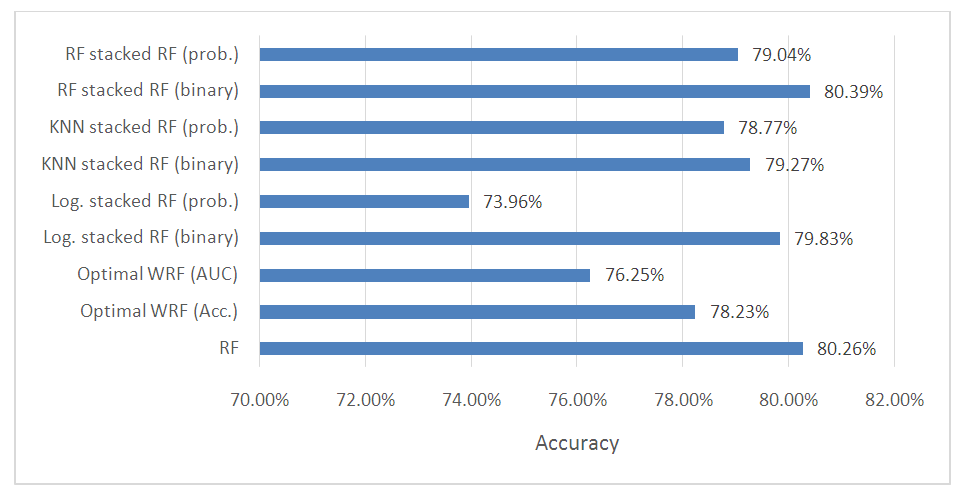Figure 3. Comparing weighted random forest classifier with regular random forest

4. Conclusions

The aim of this research was to improve the random forest, a popular machine learning model, as a classifier. Several models based on ensemble learning were developed for this purpose. The suggested models include stacking-based random forest and optimal weighted random forest using out-of-bag accuracy and AUC. The models were tested on 10 public datasets, and the findings showed that only the stacking-based random forest model was superior to the regular random forest classifier. The stacking-based random forest model, which trains a 2^nd level of random forest on inner randomly created decision trees, outperformed all other generated models. After this study, future research may be explored the directions: finding an optimal weight solution through additional optimization techniques [16,17], and combining bagged and boosted trees to enhance prediction accuracy while reducing bias and variance. Developing a comparable framework to enhance random forest regressor; and applying the same concept to other fields or research, such as data envelopment analysis (DEA) [18,19,20].