-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2024; 14(1): 1-6
doi:10.5923/j.statistics.20241401.01
Received: Dec. 22, 2023; Accepted: Jan. 7, 2024; Published: Jan. 10, 2024

Coping with Seasonal Effects of Global Warming in the Estimation of Second Moments
Erhard Reschenhofer
Retired from University of Vienna, Austria
Correspondence to: Erhard Reschenhofer, Retired from University of Vienna, Austria.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Estimates of the autocorrelation in monthly temperature series are obtained in two steps. Firstly, a proper seasonal-adjustment method is applied which also works in the case of a time-varying seasonal pattern. Secondly, the seasonally adjusted series are subjected to a simple graphical procedure which enables the immediate and unbiased assessment of the magnitude of the first-order autocorrelation. The highest values occur in the northern part of the subpolar gyre. The autocorrelation there rises in the early 1940s from around 0.7 to around 0.8 and finally in the late 1990s to just under 0.9. The changes happen abruptly rather than steadily. There are no indications of a further rise beyond 0.9 towards 1, which some researchers would interpret as a sign of an imminent collapse of the Atlantic Meridional Overturning Circulation. On the contrary, there are indications that global warming is finally catching up with this region too. The consequence of this development would be that the rising trend will mask the Atlantic Multidecadal Oscillation, which contributes significantly to the autocorrelation, and thereby cause even a drop in the autocorrelation. Overall, the results are ambivalent. On the one hand, the new methods allow for more precise and up-to-date tracking of early-warning signs. On the other hand, the empirical evidence points to structural breaks and identification problems that make it impossible at this point in time to determine whether and when the system will collapse.
Keywords: Seasonal adjustment, Detrending, AMOC collapse, Early-warning signs, Autocorrelation
Cite this paper: Erhard Reschenhofer, Coping with Seasonal Effects of Global Warming in the Estimation of Second Moments, International Journal of Statistics and Applications, Vol. 14 No. 1, 2024, pp. 1-6. doi: 10.5923/j.statistics.20241401.01.
Article Outline
1. Introduction
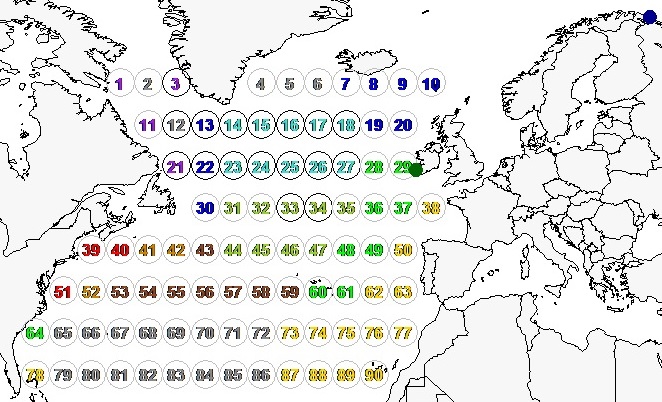
- It does not happen often that the results of a largely statistical study make it into the headlines of the major international news media. One example is the prediction of the imminent collapse of the Atlantic Meridional Overturning Circulation (AMOC) by Ditlevsen & Ditlevsen (2023). In view of the significance of such an event for the global climate, it is not surprising that their study has caused quite a stir. However, Reschenhofer (2023a) pointed out some of the weaknesses of this study. Indeed, it looks at first glance like voodoo statistics when the possible transition from the present strong AMOC mode to a weak AMOC mode is equated with the transition of some AMOC proxy from a stationary state with first-order autocorrelation ρ less than one to a nonstationary state with ρ=1. This magical connection results from the choice of a specific stochastic differential equation for the description of the dynamics of the AMOC proxy and the application of a set of more or less plausible assumptions and approximations (for an in-depth critical examination see Reschenhofer, 2023a). But even if there were no serious flaws in this approach, there would still be the difficult task of extrapolating the autocorrelation. The underlying dynamic model provides only the monotone transformation intended to make the increase in autocorrelation reasonably linear. The beginning of the rise in autocorrelation and the size of the rolling estimation window must be chosen in a more subjective manner. Ditlevsen & Ditlevsen (2023) accomplished this by trying out many different values, which clearly increases the risk of a data-snooping bias and impairs any subsequent inference. But that does not matter anyway in view of Reschenhofer’s (2023a) finding that the autocorrelation increases erratically rather than steadily, which makes forecasting based on extrapolation basically impossible. Apart from methodological issues, there are also data issues. Since direct measurements of the AMOC are only available for relatively short periods (Smeed et al., 2014), proxies for the strength of the AMOC must be used instead. Such a proxy is typically defined as the difference between the mean sea surface temperature (SST) in some northern sea region with below-average warming and some global or hemispheric benchmark. The most widely used region is the subpolar gyre (see Rahmstorf et al., 2015), which contains the 17 grid points represented by circles with black borders in Figure 1. Examples of benchmarks are the Northern Hemisphere mean surface temperature (Rahmstorf et al., 2015) and the global mean SST (Caesar et al., 2018). Ditlevsen and Ditlevsen (2023) used two times the global mean SST in order to compensate for polar amplification (see Holland and Bitz, 2003). However, Reschenhofer (2023a) argued that the subtraction of a benchmark may be counterproductive when the main task is to monitor early-warning signs like a rising autocorrelation. For the estimation of autocorrelation, the trend must be removed anyway, regardless of whether it is just the regional trend or the combined regional and global trend. So all that remains is the noise. But why would anyone want to pollute the interesting regional measurements with global noise or even two times global noise?
2. Seasonal Adjustment and Detrending
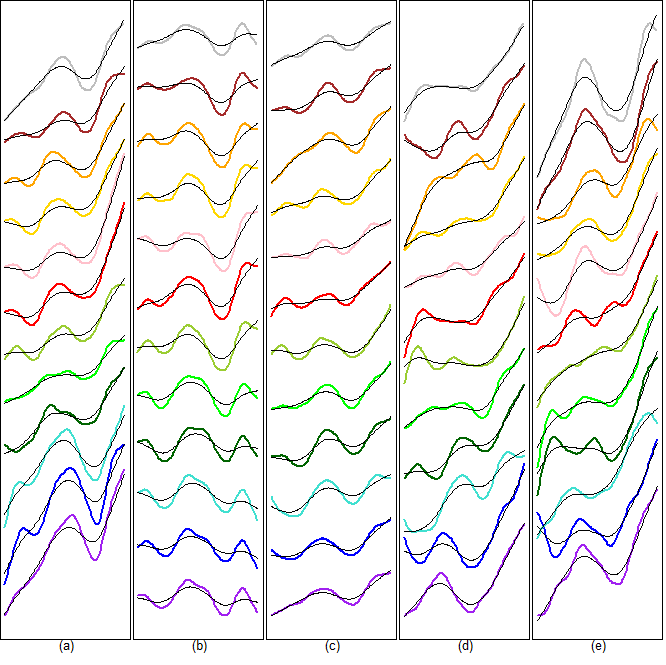
- The dataset HadCRUT5 Analysis, which combines land [CRUTEM5] and marine [HadSST4] temperature anomalies from the base period 1961-1990 on a 5° by 5° grid with greater geographical coverage via statistical infilling (Morice et al., 2021), was downloaded from the website https://crudata.uea.ac.uk/cru/data/temperature/ of the Climatic Research Unit (CRU) of the University of East Anglia. Station data were downloaded from the website //data.giss.nasa.gov/gistemp/ of NASA's Goddard Institute for Space Studies (GISS). These are adjusted, cleaned data, homogenized to account for urban effects (GISTEMP Team, 2023; Lenssen et al., 2019). The common analysis period for both types of time series is from January 1880 to November 2023 (n=1727 months). For the statistical analysis, the free statistical software R (R Core Team, 2022) was used. Figure 1 shows nine clusters of grid points with similar temperature trends according to Reschenhofer (2023b) as well as the meteorological stations Valentia Observatory (51.9394N, 10.2219W) and Vardo (70.3670N, 31.1000E). The main reason for the selection of these two stations was the availability of the data. There is only one missing value in the case of Valentia Observatory, namely in November 1942, which was replaced by the average of the values in October 1942, December 1942, November 1941, and November 1943, and also only one missing value in the case of Vardo, namely February 2023, which was replaced by the average of the values in January 2023, March 2023, and February 2022. In addition to the two stations, three grid points were selected for further analysis, namely 11, 16, and 29. The first represents the cluster with the most noticeable changes in the seasonal pattern (see Reschenhofer, 2023b), the second represents the northern part of the subpolar gyre, and the third is of interest because of its proximity to Valentia Observatory. The data from CRU are anomalies from the base period 1961-1990 whereas the data from GISS are absolute values. In the case of the anomalies, a seasonal pattern only becomes visible when it changes over time. Let
 be any one of the five time series of anomalies or absolute values. For each calendar month, i.e., j=1,...,12, the trend of the subseries
be any one of the five time series of anomalies or absolute values. For each calendar month, i.e., j=1,...,12, the trend of the subseries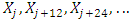 | (1) |
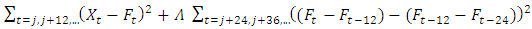 | (2) |
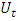 remaining after seasonal adjustment and detrending, the statistics
remaining after seasonal adjustment and detrending, the statistics 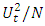 and
and 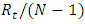 were plotted cumulatively against time, where
were plotted cumulatively against time, where 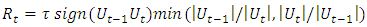 | (3) |
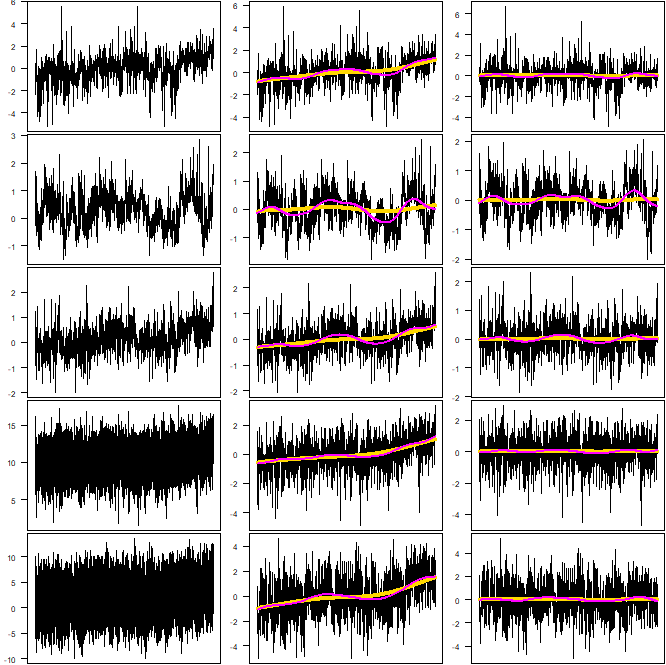
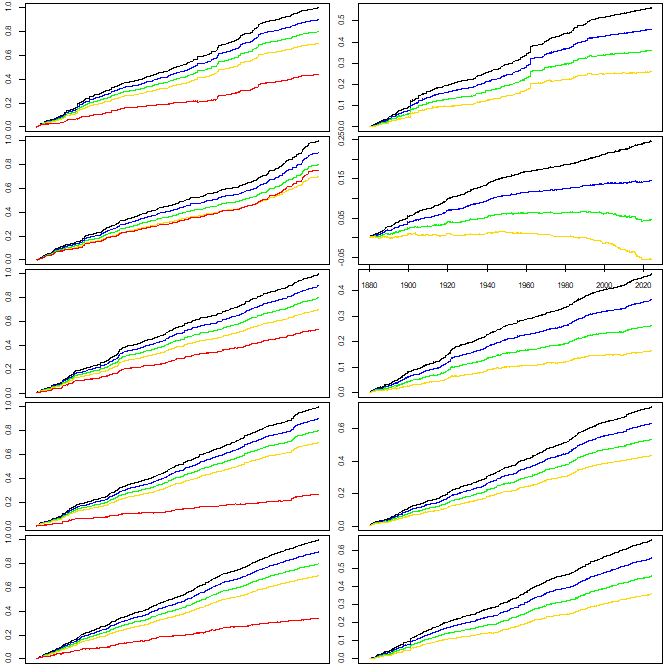
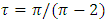 (Reschenhofer, 2017a, 2017b, 2019). These cumulative graphs allow the detection of any changes without the delay caused by a large estimation-window width of 50 (Ditlevsen and Ditlevsen, 2023) or even 70 years (Boers, 2021). Remarkably, the actual changes in the variance (shown in the first column of Figure 4) and the autocorrelation (in the second column) are easier to explain by structural breaks in the slope than by a steady growth of the slope, which corroborates earlier findings (Reschenhofer, 2023a, 2023b). Regarding the differences between the different adjustment methods, one would expect that any remaining part of the seasonal pattern will cause a rise both in variance and autocorrelation. Indeed, the variance appears to be consistently higher whenever a naive adjustment method is used. To a lesser extent, this is also true for the autocorrelation.
(Reschenhofer, 2017a, 2017b, 2019). These cumulative graphs allow the detection of any changes without the delay caused by a large estimation-window width of 50 (Ditlevsen and Ditlevsen, 2023) or even 70 years (Boers, 2021). Remarkably, the actual changes in the variance (shown in the first column of Figure 4) and the autocorrelation (in the second column) are easier to explain by structural breaks in the slope than by a steady growth of the slope, which corroborates earlier findings (Reschenhofer, 2023a, 2023b). Regarding the differences between the different adjustment methods, one would expect that any remaining part of the seasonal pattern will cause a rise both in variance and autocorrelation. Indeed, the variance appears to be consistently higher whenever a naive adjustment method is used. To a lesser extent, this is also true for the autocorrelation. 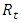 is a severely biased estimator for the first-order autocorrelation ρ unless ρ is close to zero. However, when we are mainly interested whether ρ is rising or not, a possible bias does not matter that much. Nevertheless, an alternative, unbiased monitoring procedure will be used in the next section.
is a severely biased estimator for the first-order autocorrelation ρ unless ρ is close to zero. However, when we are mainly interested whether ρ is rising or not, a possible bias does not matter that much. Nevertheless, an alternative, unbiased monitoring procedure will be used in the next section.3. Estimation of Autocorrelation
- Assuming that any trend or seasonal pattern has already been removed from the time series
 by subtracting monthly HP trends (as described in Section 2), the current variance and first-order autocovariance can easily be estimated by
by subtracting monthly HP trends (as described in Section 2), the current variance and first-order autocovariance can easily be estimated by 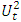 and
and 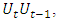 respectively. In the case of the first-order autocorrelation, it is not that simple. The replacement of the highly unstable least squares estimator
respectively. In the case of the first-order autocorrelation, it is not that simple. The replacement of the highly unstable least squares estimator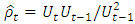 | (4) |
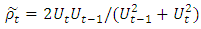 | (5) |
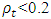 (see Reschenhofer, 2017a) is certainly highly implausible (see Figure 4). So, if we are also interested in the size of the autocorrelation and not just whether it goes up or down, we need an alternative method. For the determination of the direction alone it would be sufficient to plot the statistics (3) or (5) cumulatively against time. In contrast, plotting the statistics
(see Reschenhofer, 2017a) is certainly highly implausible (see Figure 4). So, if we are also interested in the size of the autocorrelation and not just whether it goes up or down, we need an alternative method. For the determination of the direction alone it would be sufficient to plot the statistics (3) or (5) cumulatively against time. In contrast, plotting the statistics 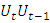 seems to be pointless at first glance because it is impossible to tell whether a rise in the auto-covariance is due to a rise in the variance or a rise in the autocorrelation. At second glance it is the solution. Indeed, plotting the statistics
seems to be pointless at first glance because it is impossible to tell whether a rise in the auto-covariance is due to a rise in the variance or a rise in the autocorrelation. At second glance it is the solution. Indeed, plotting the statistics 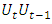 together with the statistics
together with the statistics 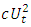 for various values of
for various values of 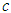 allows the unknown auto-correlation to be determined with sufficient accuracy for practical use. Alternatively, the differences
allows the unknown auto-correlation to be determined with sufficient accuracy for practical use. Alternatively, the differences 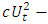
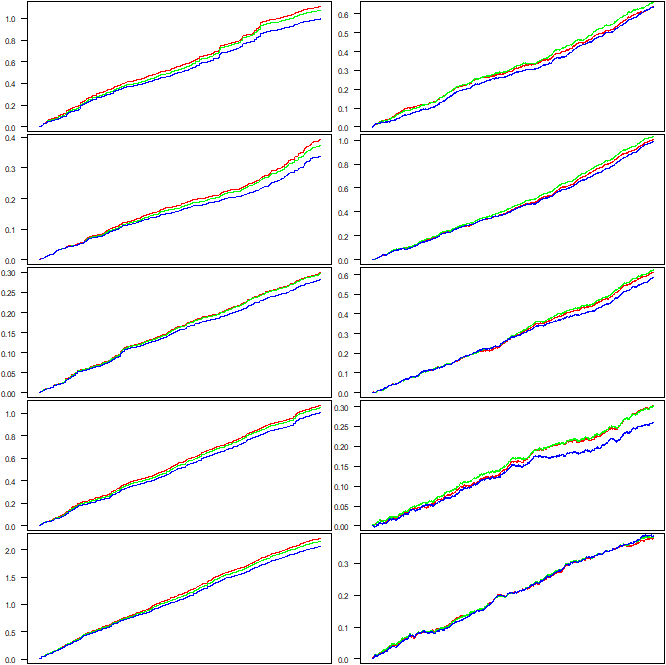
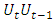 can be plotted which often results in a clearer display. Both types of plots are shown in Figure 5. The autocorrelation is very weak in the case of the two stations and very high in the case of grid point 16 which lies in the subpolar gyre and can therefore possibly serve as an indicator for the strength of the AMOC. In the latter case, the cumulative differences
can be plotted which often results in a clearer display. Both types of plots are shown in Figure 5. The autocorrelation is very weak in the case of the two stations and very high in the case of grid point 16 which lies in the subpolar gyre and can therefore possibly serve as an indicator for the strength of the AMOC. In the latter case, the cumulative differences 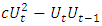 are remarkably flat for c=0.7 (yellow line) until the early 1940s, for c=0.8 (green line) until the late 1990s, and finally slightly increasing for c=0.9 (blue line), indicating that the autocorrelation is first about 0.7, then about 0.8, and finally slightly below 0.9. In each period, the respective cumulative graph is roughly linear. Moreover, there is no indication of a smooth transition from one period to the next. The transitions rather look like structural breaks.
are remarkably flat for c=0.7 (yellow line) until the early 1940s, for c=0.8 (green line) until the late 1990s, and finally slightly increasing for c=0.9 (blue line), indicating that the autocorrelation is first about 0.7, then about 0.8, and finally slightly below 0.9. In each period, the respective cumulative graph is roughly linear. Moreover, there is no indication of a smooth transition from one period to the next. The transitions rather look like structural breaks. 4. Discussion
- The prediction of an imminent collapse of the AMOC (Ditlevsen and Ditlevsen, 2023) is based on a specific dynamic model for a specific AMOC proxy and on the assumption that the model parameter λ, which is related to the first-order autocorrelation ρ of the AMOC proxy via
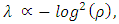 | (6) |
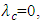 where the dynamical system will move to a different state. While the model and the proxy have already been discussed at length in previous papers (Reschenhofer, 2023a, 2023b), the focus of the present paper is solely on the estimation of ρ, which is an important part of the prediction because the time of transition is found by extrapolating estimates of ρ up to the point where the value 1 is reached. In light of evidence that global warming affects the different seasons differently, the standard method to remove seasonal patterns by simply subtracting monthly means is not suitable. Instead, HP smoothing is carried out separately for each calendar month, which allows to remove trends and seasonal patterns simultaneously just by subtracting the HP trends. This method saves the effort to keep time-changing trends and time-changing seasonal patterns cleanly apart. After the removal of any trend and seasonal pattern, the time-changing autocorrelation of the residuals
where the dynamical system will move to a different state. While the model and the proxy have already been discussed at length in previous papers (Reschenhofer, 2023a, 2023b), the focus of the present paper is solely on the estimation of ρ, which is an important part of the prediction because the time of transition is found by extrapolating estimates of ρ up to the point where the value 1 is reached. In light of evidence that global warming affects the different seasons differently, the standard method to remove seasonal patterns by simply subtracting monthly means is not suitable. Instead, HP smoothing is carried out separately for each calendar month, which allows to remove trends and seasonal patterns simultaneously just by subtracting the HP trends. This method saves the effort to keep time-changing trends and time-changing seasonal patterns cleanly apart. After the removal of any trend and seasonal pattern, the time-changing autocorrelation of the residuals 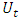 can be estimated. In order to avoid any delay caused by using a rolling estimation window, this is done by examining the slopes of the cumulative differences
can be estimated. In order to avoid any delay caused by using a rolling estimation window, this is done by examining the slopes of the cumulative differences 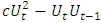 for various values of c. The results obtained for the sea surface temperature in a region that is often used for the construction of AMOC proxies show that ρ is still smaller than 0.9 and there is no indication of a further increase toward 1. The method of predicting the time of a possible AMOC collapse by extrapolation therefore lacks any basis.
for various values of c. The results obtained for the sea surface temperature in a region that is often used for the construction of AMOC proxies show that ρ is still smaller than 0.9 and there is no indication of a further increase toward 1. The method of predicting the time of a possible AMOC collapse by extrapolation therefore lacks any basis. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML