-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2023; 13(1): 20-26
doi:10.5923/j.statistics.20231301.03
Received: Nov. 7, 2022; Accepted: Jan. 21, 2023; Published: Jul. 24, 2023

Application of EM Algorithm in Classification Problem & Parameter Estimation of Gaussian Mixture Model
Felix N. Nwobi1, Stephen I. Kalu1, 2
1Department of Statistics, Imo State University, Owerri, Nigeria
2Department of Statistics, Abia State Polytechnic, Aba, Nigeria
Correspondence to: Stephen I. Kalu, Department of Statistics, Imo State University, Owerri, Nigeria.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The problem of misclassification in a k-group scenario which involves identifying any component from which each group elements is drawn from is studied in this paper. These problems were modeled as a Gaussian mixture model while, the expectation maximization algorithm (EM) was used in the estimation of the parameters for the identification of the group where each group elements is drawn from. Two data sets were used in this paper; the weights of 1000 students and the weights of 200 babies at birth. Results show that 70% correct classification rate, attributing 30% to misclassification using data set 1 and 74.5% correct classification rate, attributing 25.5% to misclassification using data set 2, were achieved.
Keywords: Mixture Models, Estimation in mixture models, Gaussian mixture models, EM Algorithm, Classification in Gaussians
Cite this paper: Felix N. Nwobi, Stephen I. Kalu, Application of EM Algorithm in Classification Problem & Parameter Estimation of Gaussian Mixture Model, International Journal of Statistics and Applications, Vol. 13 No. 1, 2023, pp. 20-26. doi: 10.5923/j.statistics.20231301.03.
Article Outline
1. Introduction
- According to Lindsay (1995), Mixture Models (MM) as probabilistic models are used for representing the presence of population subsets located within an overall population. Mixture models provide a much wider range of modeling possibilities and capabilities than the single component model. Some details of MM can be found in Bohning and Seidel (2003) and Bohning et al. (2007).For estimation involving mixture models, various analytical methods have been developed for estimating
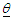 (a parameter space) in finite mixture models. There are many methods of estimating the parameters of a MM, four of such methods are method of moments, minimum distance method, Bayesian method and maximum likelihood (ML) method.Pearson’s (1894) method of moments is one of the earliest methods for estimating the parameters from finite mixture models. This method held sway until the advent of modern computers to compute the maximum of the log-likelihood function. Some developments in the method of moment estimation can be found in Lindsay & Basak (1993), Furman & Lindsay (1994a, b), Lindsay (1995), Withers (1996) and Craigmile & Titherington (1998). Minimum distance estimation methods introduced by Wolfowitz (1957) is a general method for estimating
(a parameter space) in finite mixture models. There are many methods of estimating the parameters of a MM, four of such methods are method of moments, minimum distance method, Bayesian method and maximum likelihood (ML) method.Pearson’s (1894) method of moments is one of the earliest methods for estimating the parameters from finite mixture models. This method held sway until the advent of modern computers to compute the maximum of the log-likelihood function. Some developments in the method of moment estimation can be found in Lindsay & Basak (1993), Furman & Lindsay (1994a, b), Lindsay (1995), Withers (1996) and Craigmile & Titherington (1998). Minimum distance estimation methods introduced by Wolfowitz (1957) is a general method for estimating 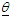 in a finite mixture, have been discussed by William et al. (1982) and Titherington et al. (1985).Another method for estimating
in a finite mixture, have been discussed by William et al. (1982) and Titherington et al. (1985).Another method for estimating 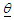 is the Bayesian method. Many reasons abound why some researchers are inclined to using Bayesian method of estimation while dealing with a finite MM (Fruhwirth-Schnatter, 2006). The reasons for these are the introduction of a suitable prior distribution or
is the Bayesian method. Many reasons abound why some researchers are inclined to using Bayesian method of estimation while dealing with a finite MM (Fruhwirth-Schnatter, 2006). The reasons for these are the introduction of a suitable prior distribution or 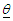 that eliminates spurious modes in the course of maximizing the log-likelihood function, and secondly, in the case where the posterior distribution for the unknown parameters is handy, this method provides reliable inference without recourse to the asymptotic normality of the distributions. These are the inherent advantages associated to this method especially when the sample size
that eliminates spurious modes in the course of maximizing the log-likelihood function, and secondly, in the case where the posterior distribution for the unknown parameters is handy, this method provides reliable inference without recourse to the asymptotic normality of the distributions. These are the inherent advantages associated to this method especially when the sample size 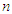 is small
is small 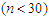 , since the asymptotic theory of MLE can be implemented when
, since the asymptotic theory of MLE can be implemented when 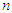 is quite large
is quite large 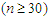 .The fourth method for estimating the parameters of a finite MMs is the ML Estimation method. Likelihood based inference has enjoyed tremendous and fast developments and has contributed immensely towards resolving estimation problems involving finite MMs. Since the explicit expression for the MLE’s are typically unavailable, then a numerical EM Algorithm is used for maximizing the log-likelihood function. The expectation-Maximization (EM) Algorithm is one of the methods frequently in use according to Dempster et al. (1977). We can find more details about this methods in McLachlan and Krishna (1997), McLachlan and Peel (2000), Oleszak (2020), Kuroda (2021) and Smyth (2021).The aim of this paper is to implement classification procedure on the Gaussian mixture model involving 2 groups
.The fourth method for estimating the parameters of a finite MMs is the ML Estimation method. Likelihood based inference has enjoyed tremendous and fast developments and has contributed immensely towards resolving estimation problems involving finite MMs. Since the explicit expression for the MLE’s are typically unavailable, then a numerical EM Algorithm is used for maximizing the log-likelihood function. The expectation-Maximization (EM) Algorithm is one of the methods frequently in use according to Dempster et al. (1977). We can find more details about this methods in McLachlan and Krishna (1997), McLachlan and Peel (2000), Oleszak (2020), Kuroda (2021) and Smyth (2021).The aim of this paper is to implement classification procedure on the Gaussian mixture model involving 2 groups 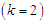 and to identify the component from which each group elements probably belongs to, and as well as to estimate the respective parameters of the groups and their mixture weights. The EM Algorithm procedures were implemented in this paper using MATLAB.
and to identify the component from which each group elements probably belongs to, and as well as to estimate the respective parameters of the groups and their mixture weights. The EM Algorithm procedures were implemented in this paper using MATLAB.2. Methods
- Let
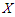 be a random variable from a normal population. Let also
be a random variable from a normal population. Let also 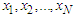 be a random sample from
be a random sample from 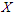 that constitute two groups, such that
that constitute two groups, such that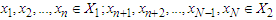 where
where 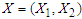 .According to Wirjanto (2009), we assume that
.According to Wirjanto (2009), we assume that 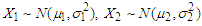 . The Gaussian distribution is defined as
. The Gaussian distribution is defined as 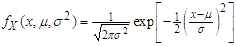 | (1) |
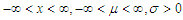 , so that the probability density function of mixture of Gaussians will be given as
, so that the probability density function of mixture of Gaussians will be given as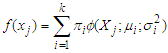 | (2) |
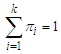 and
and 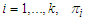 are the mixing parameter weights.In two component Gaussian mixture models,
are the mixing parameter weights.In two component Gaussian mixture models, 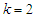 and
and 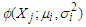 is the PDF of a normal distribution with finite mean
is the PDF of a normal distribution with finite mean 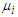 and finite variance
and finite variance 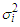 . The number of estimable parameters of the Gaussian mixture distributions is given by the formula
. The number of estimable parameters of the Gaussian mixture distributions is given by the formula 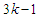 so that if
so that if 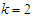 , as in our case,
, as in our case, 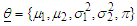 .
.2.1. Implementation Procedure of EM Algorithm
- Dempster et al (1977) and Wu (1985) have proposed the use of initial guesses for the parameters
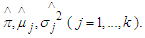 Soderlind (2010) in line with Dempster et al (1977) and Wu (1985) suggested using
Soderlind (2010) in line with Dempster et al (1977) and Wu (1985) suggested using 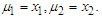 Both
Both 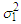 and
and 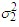 can be set equal to the overall sample variance
can be set equal to the overall sample variance 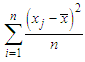 Here, we take
Here, we take 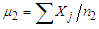 , similarly for
, similarly for 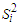 . We initialize the mixing proportion at
. We initialize the mixing proportion at 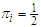 . (a) e-step:Following Huber (1964), for a given number of an observed data, we can evaluate the corresponding posterior probabilities, called responsibilities as follows
. (a) e-step:Following Huber (1964), for a given number of an observed data, we can evaluate the corresponding posterior probabilities, called responsibilities as follows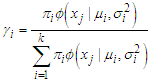 | (3) |
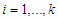 and
and 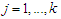 (b) m-step:Now, we compute the weighted means and variances using the obtained responsibilities in (3) as
(b) m-step:Now, we compute the weighted means and variances using the obtained responsibilities in (3) as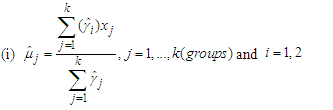 | (4) |
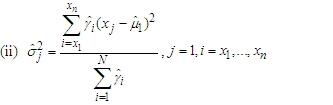 | (5) |
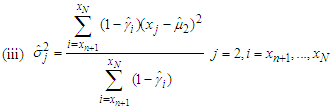 | (6) |
 | (7) |
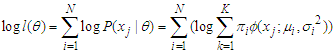 | (8) |
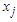 as a random variable with a two component Gaussian mixture as follows: Representing the mixture mean weight as
as a random variable with a two component Gaussian mixture as follows: Representing the mixture mean weight as 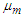 and that of the mixture variance weight
and that of the mixture variance weight 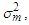 then the respective mixture mean and variance weights can be estimated respectively as
then the respective mixture mean and variance weights can be estimated respectively as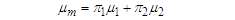 | (9) |
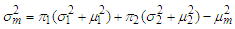 | (10) |
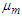 and
and 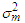 is the up-dated mean and variance of the Gaussian mixture after each iterative step of the EM Algorithm.
is the up-dated mean and variance of the Gaussian mixture after each iterative step of the EM Algorithm. 2.2. Classification with Gaussians
- We used Bayes’ Theorem for our problem to relate the probability density function of the data,
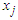 , given the class to the posterior probability or the class given the data. Considering our univariate data consisting of a set of random variable
, given the class to the posterior probability or the class given the data. Considering our univariate data consisting of a set of random variable 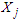 , whose PDFs, given
, whose PDFs, given 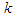 , are Gaussians with means
, are Gaussians with means 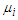 and variances
and variances 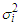 . Using Bayes’ theorem, we specify the component probability density function as;
. Using Bayes’ theorem, we specify the component probability density function as;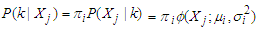 | (11) |
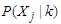 is the likelihood of class
is the likelihood of class 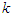 given observation
given observation 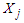 . Probability of misclassification is a measure of the likelihood that individuals or objects are classified wrongly. We have two types of misclassification error as;1. To classify into population
. Probability of misclassification is a measure of the likelihood that individuals or objects are classified wrongly. We have two types of misclassification error as;1. To classify into population 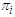 given that it is actually from population
given that it is actually from population 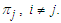 2. To classify into population
2. To classify into population 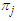 given that it is actually from population
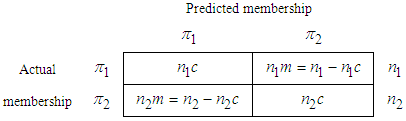
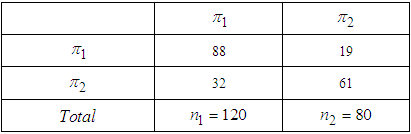
given that it is actually from population 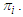 Following Richard et al. (2007), we classify the classification against the true group by creating a Statistician’s Confusion Matrix as in Table 1. Apparent error rate can be defined as the measure of performance in classification that does not depend on the form of the parent population. This rate is the fraction of observed values in the training sample that are misclassified by the sample classification function and can be calculated for any classification procedure. The confusion matrix is of the form
Following Richard et al. (2007), we classify the classification against the true group by creating a Statistician’s Confusion Matrix as in Table 1. Apparent error rate can be defined as the measure of performance in classification that does not depend on the form of the parent population. This rate is the fraction of observed values in the training sample that are misclassified by the sample classification function and can be calculated for any classification procedure. The confusion matrix is of the form
|
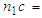 Number of
Number of 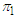 objects that are correctly classified as
objects that are correctly classified as 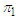 objects
objects 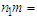 Number of
Number of 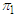 objects misclassified as
objects misclassified as 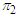 objects
objects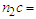 Number of
Number of 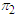 objects that are correctly classified into
objects that are correctly classified into 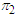 objects
objects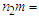 Number of
Number of 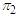 objects that are misclassified into
objects that are misclassified into 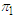 objects.The formula error rate is given as
objects.The formula error rate is given as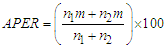 | (12) |
3. Results and Discussions
- Two data sets were used. Data Set 1are weights of male and female first year students of Abia State Polytechnic, Aba. Data Set 2 consists of weights of 120 males and 80 female babies at birth from Federal Medical Centre (FMC), Owerri, Imo State. See data on Appendix A, B and C. In this section, we used MATLAB source codes to implement the EM Algorithm procedures and as well, carry out the data classification analysis.
3.1. Result of the Expectation Step
- Using Data set 1, taking initial values for
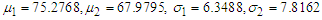 . We also take the overall mean
. We also take the overall mean 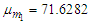 .
. 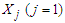 is an
is an 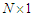 column vector of the combined weights of male female students. We generate the probabilities for each of the data points. This step helps us in allocating the distinct mixture observations to previously defined groups. See equations (1) - (7) in page 3-4. Using Data set 2, the Algorithm was initialized with the following parameter values,
column vector of the combined weights of male female students. We generate the probabilities for each of the data points. This step helps us in allocating the distinct mixture observations to previously defined groups. See equations (1) - (7) in page 3-4. Using Data set 2, the Algorithm was initialized with the following parameter values, 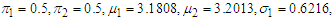
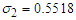 , taking its overall initial mean as
, taking its overall initial mean as 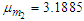 . In this case,
. In this case, 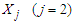 is a
is a 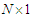 column vector of the combined baby weights at birth. Data set 1 consist of
column vector of the combined baby weights at birth. Data set 1 consist of 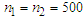 while in Data set 2,
while in Data set 2, 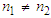 since,
since, 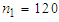 and
and 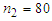 .
.3.2. Results of the Maximization Step
- For us to obtain the log-likelihood and the mixing proportions using Data sets 1 & 2, we applied the MATLAB code in Appendix F. This approach, maximizes the E-Step and outputs the optimal mixing weights using data set 1 as
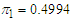 ,
,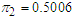 and component means as
and component means as 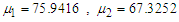 & component variances as
& component variances as 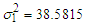 ,
, 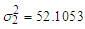 . Using data set 2 in the same manner, we obtained the final requisite parameter up-dates as
. Using data set 2 in the same manner, we obtained the final requisite parameter up-dates as 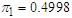 ,
, 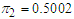 , component means as
, component means as 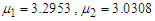 , and component variances as
, and component variances as 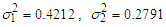 . See equations (9) - (10) in page 4 of this paper.
. See equations (9) - (10) in page 4 of this paper.3.3. Results of the EM Algorithm
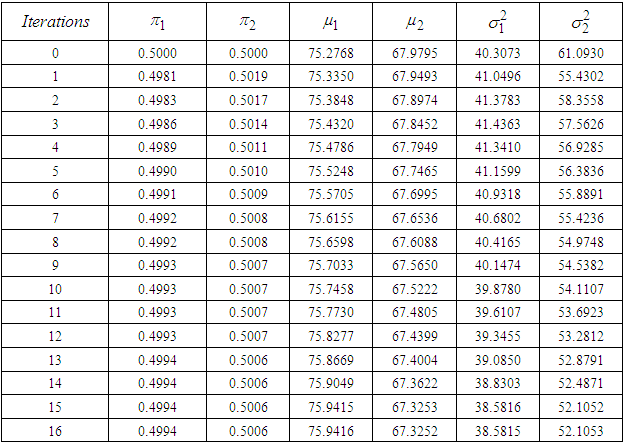
- Data set 1 After our implementation of the EM algorithm using data set 1, the iterated maximum likelihood estimates for the parameters are contained in Table 2.
|
|
3.4. Description of the Iteration Procedure Using Data Set 1&2
- To implement the EM Algorithm iterative procedure to our data sets, we applied the following sequence of operation INITIALIZATIONData set 1 initial values:
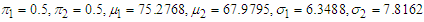 Data set 2 initial values:
Data set 2 initial values: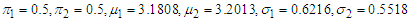 Expectation step:1. Input: (Slot in the initial values for either data set 1 or 2 into the source codes of Appendix D)Output: A set of with weights that maximizes the log-likelihood function of equation (8) will be generated.Maximization step:2. Update the mixture model parameters with the computed output weights from E-step using the MATLAB source codes in Appendix E.3. Stopping criteria: If stopping rule are satisfied (convergence of parameters and log-likelihood) then we stop, else we set
Expectation step:1. Input: (Slot in the initial values for either data set 1 or 2 into the source codes of Appendix D)Output: A set of with weights that maximizes the log-likelihood function of equation (8) will be generated.Maximization step:2. Update the mixture model parameters with the computed output weights from E-step using the MATLAB source codes in Appendix E.3. Stopping criteria: If stopping rule are satisfied (convergence of parameters and log-likelihood) then we stop, else we set 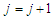 and go back to step 1 and input the updated parameter values for the next iteration.
and go back to step 1 and input the updated parameter values for the next iteration. 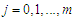 . Where
. Where 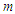 is the
is the 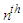 number at which convergence or optimality conditions was achieved. Stopping Rule: When all the epsilon
number at which convergence or optimality conditions was achieved. Stopping Rule: When all the epsilon 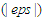 values are less than or equal to 0.0001
values are less than or equal to 0.0001 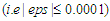 , or the values of all
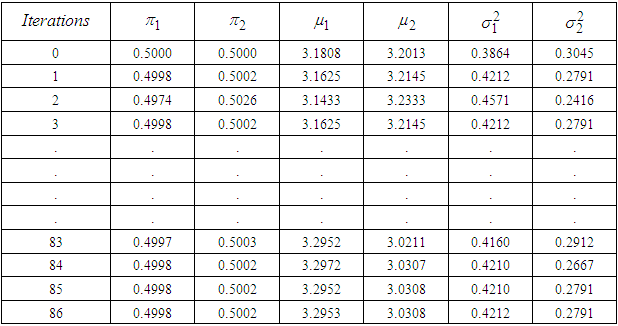
, or the values of all 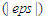 appears not to be changing significantly from one iterative step to another, then we assume that the EM solution is optimal at that point and cannot be improved upon further. The values of the complete iterations are contained in Table 3 and Table 4 of this paper.
appears not to be changing significantly from one iterative step to another, then we assume that the EM solution is optimal at that point and cannot be improved upon further. The values of the complete iterations are contained in Table 3 and Table 4 of this paper.3.5. Result of the Classification Using Data Set 1
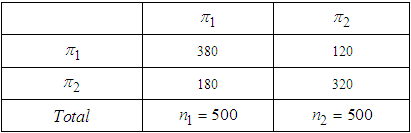
- After implementing the classification procedures on the maximized generated posterior probabilities using equation (11) & (12), we obtained the following confusion matrix. See Appendix G for the MATLAB’s source codes for deriving the discriminant values of Table 4 and Table 5.
|
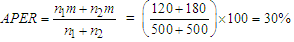
3.6. Result of the Classification Using Data Set 2
|
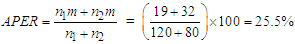
4. Conclusions
- From this paper, we explained the intricacies of how to estimate the parameters of two combined Gaussian models as well as their classifications using EM Algorithm procedure. We also explained exhaustively the actual estimation of these model parameters using sets of sample data, namely data set for the weights of students and data set 2 for the weights of babies at birth.Table 2 of our analysis displayed the estimated maximized values of the relevant parameters for the Gaussian mixture model using data set 1, while Table 3 showed the estimated maximized values of the parameters for the mixture model using data set 2. Having a look at the both ends of Table 2 & Table 3, revealed that convergences have been achieved, since the parameter estimates stopped changing significantly at those points and
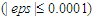 . Table 4 presents the result of classification using data set 1, whose interpretation implies that we misclassified data set 1 by about 30% failure rate, attributing 70% to correct classification rate. Table 5 at the other hand showed that we misclassified the data set 2 by about 25.5%, having a classification success rate of 74.5%. However, the overall classification efficiency of the Algorithm based on the output of sample data can be considered high, since 70% of Data set 1 and 74.5% of Data set 2 were correctly classified by the Algorithm. These validations achieved by the sample data procedures suggest that EM Algorithm may be useful as early warning statistical tool for parameter estimation and for predicting and classifying the mixture of Gaussians.
. Table 4 presents the result of classification using data set 1, whose interpretation implies that we misclassified data set 1 by about 30% failure rate, attributing 70% to correct classification rate. Table 5 at the other hand showed that we misclassified the data set 2 by about 25.5%, having a classification success rate of 74.5%. However, the overall classification efficiency of the Algorithm based on the output of sample data can be considered high, since 70% of Data set 1 and 74.5% of Data set 2 were correctly classified by the Algorithm. These validations achieved by the sample data procedures suggest that EM Algorithm may be useful as early warning statistical tool for parameter estimation and for predicting and classifying the mixture of Gaussians. Appendix D
- The E-step: See William (2008) for Appendix D, E and F.
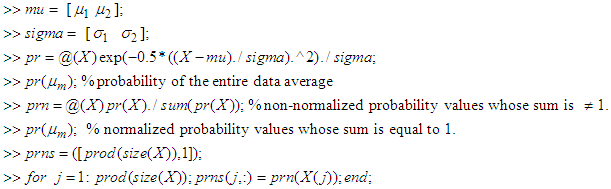
 % outputs the normalized posterior probabilities from 1 to 10. Hence, in our Algorithm, we replaced 10 with 1000 or 200 as the case may require. Note:
% outputs the normalized posterior probabilities from 1 to 10. Hence, in our Algorithm, we replaced 10 with 1000 or 200 as the case may require. Note: 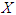 is the entire data for student weights or baby weights at birth.
is the entire data for student weights or baby weights at birth. 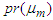 is the entire mean of either data set 1 or data set 2 as the case may also demand.
is the entire mean of either data set 1 or data set 2 as the case may also demand. Appendix E
- The M-step source codes
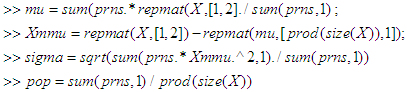
Appendix F
- MATLAB’s Source codes for the Log-likelihood and the mixing proportions.
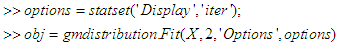
Appendix G
- MATLAB’s Source codes for the classification/Discriminant Analysis:For Data Set 1
 For Data Set 2
For Data Set 2
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML