-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2023; 13(1): 13-19
doi:10.5923/j.statistics.20231301.02
Received: Jun. 5, 2023; Accepted: Jun. 21, 2023; Published: Jul. 12, 2023

Statistical Analysis of Unsteady, Spatially-Varying Shock Wave Characteristics within a Supersonic Flow Environment
Ward Manneschmidt, Phil Ligrani
Mechanical and Aerospace Engineering Department, University of Alabama in Huntsville, Huntsville, Alabama, USA
Correspondence to: Phil Ligrani, Mechanical and Aerospace Engineering Department, University of Alabama in Huntsville, Huntsville, Alabama, USA.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The present study provides a new statistical analysis method to track and quantify instantaneous shock wave motions. Correlation and spectral analysis approaches are then applied to the resulting digitized data to provide information on unsteady shock wave dynamics. The most physically relevant magnitude squared coherence results are based upon tracked locations of both the normal shock wave and the lambda foot rearward oblique shock wave, as demonstrated by the highest coherence values for all frequencies, relative to other methods which are employed for quantification of unsteady flow characteristics. Similar conclusions are provided by power spectral density variations with frequency which are also based upon tracked locations of the two types of shock waves. Associated ensemble averaged spectra have peaks which are aligned with each other at frequencies of 8.5 Hz, 16 Hz, and 25 Hz. These peaks are also in excellent agreement with frequencies of local maxima within magnitude squared coherence distributions which are based upon tracked data analysis.
Keywords: Frequency Analysis, Correlation Analysis, Spectra, Magnitude Squared Coherence, Supersonic Flows, Shock Waves
Cite this paper: Ward Manneschmidt, Phil Ligrani, Statistical Analysis of Unsteady, Spatially-Varying Shock Wave Characteristics within a Supersonic Flow Environment, International Journal of Statistics and Applications, Vol. 13 No. 1, 2023, pp. 13-19. doi: 10.5923/j.statistics.20231301.02.
Article Outline
1. Introduction
- Statistical analysis is used for data processing and understanding for a variety of academic disciplines and research fields where complex analysis environments vary with time and three-dimensional space. For example, Kopsiaftis and Karantzalos [1] utilize and apply statistical methods to satellite-recorded digitized video data of vehicle distributions along roads to determine traffic density patterns and variations both spatially and temporally. Apte et al. [2] develop and employ spatial maps of air pollution distributions within the atmosphere above Oakland California. These are obtained from multiple measurements along and above each city street in order to produce time-averaged, three-dimensional spatial maps of air pollution. Different analysis methods are utilized by the investigators to determine their effects in regard to measurement frequency and accuracy. Another example of elaborate statistical analysis applied to a complex environment is provided by Alimissis et al. [3]. These investigators utilize a variety of different linear regression tools with machine learning algorithms to predict air pollution levels within the atmosphere above a variety of different locations around the world.The present study is unique because it provides new statistical analysis procedures which are applied to data which also quantify temporally-varying and spatially-varying physical phenomena. New and innovative approaches to these analysis procedures give results which are more physically representative and relevant, compared to data obtained with previously used statistical analysis approaches. The present study is thus important because a statistical analysis method is provided for complex data which elucidates physically relevant information. Analysis results from alternative methods are less representative of associated physical phenomena. The environment selected for analysis is a compressible, supersonic fluid flow field with different types of shock waves. Of particular interest are unsteady motions of a laboratory controlled normal shock wave, along with one of the oblique shock waves which forms part of the associated lambda foot. The complete shock wave structure develops because of complex interactions with different developing boundary layer components, which lead to separation from the wall of the approaching boundary, layer, followed by a substantial flow re-circulation zone, which is positioned along the wall and beneath the lambda foot. The positions and structural characteristics of the normal and oblique shock waves are visualized and quantified using a shadowgraph flow visualization system. Time sequences of digitized images from this system are then employed for analysis with a goal of improved understanding of unsteady shock wave characteristics and interactions. A unique and innovative part of this analysis is the employment of a statistics based shock wave tracking algorithm. This is followed by the application of spectra (or PSD, Power Spectral Density) and correlation statistical analysis approaches to the resulting digital data sequences.Previous studies which apply Power Spectral Density (PSD) analysis to shock wave position variations and other unsteady phenomena include Schmit et al. [4]. These investigators employ shadowgraph visualization data along with dynamic pressure transducers to investigate supersonic flow arrangements with oblique shock waves. The investigators apply discrete Fourier transforms to both pressure and visualization data for two different flow conditions. Also utilized is cross correlation analysis to obtain time lag information to determine time sequences of different flow events. Leptuch and Agrawal [5] employ schlieren visualization to study buoyancy effects within a helium jet. These researchers additionally utilize Fourier analysis to provide frequency information regarding flow oscillations as the jet transitions into a microgravity environment. Estruch et al. [6] also employ schlieren flow imaging to visualize unsteady behavior of an oblique shock wave. Fourier series analysis is utilized to filter the background noise from their digitized image sequences before tracking the movement of the shock wave. Fourier analysis is also employed to provide information on the frequency behavior of shock wave movement. Garg and Cattafesta [7] use schlieren imaging to study subsonic flow across a cavity. Fourier analysis and correlation analysis are applied simultaneously to photo diode data and to microphone data. The present study expands upon these previous investigations with a new statistical analysis method to track and quantify instantaneous shock wave motions. Correlation and spectral analysis approaches are then applied to the resulting data to provide physically relevant information on unsteady shock wave dynamics. Relevant to past investigations [4-7], improved clarity of time- and spatially-varying flow phenomena is provided. Such enhanced clarity is useful since related shock wave phenomena influence the operational characteristics of high performance aircraft engines and because of many unresolved questions regarding the causes and origins of shock wave unsteadiness [8-11]. The newly developed and applied statistical analysis approaches are thus useful in providing new avenues to address important and current technical issues. The statistical analysis innovations of the present investigation are also useful to the analysis of other unsteady, 3D analysis environments, including ones involving vehicle traffic tracking [1] and atmospheric air pollution distributions [2-3].
2. Experimental and Analytical Apparatus and Procedures
2.1. Experimental Facility and Shadowgraph Flow Visualization Apparatus
- The supersonic wind tunnel (which is also referred to as the SS/TS/WT or SuperSonic/TranSonic/WindTunnel) is employed to obtain the data which are analyzed within the present investigation. This facility is a blow-down-type apparatus, which is located within the Johnson Research Center of the University of Alabama in Huntsville. The low-pressure piping system used in these experiments (which is a portion of the overall piping system) consists of an air compressor, a vertical air supply tank, a series of pressure relief valves, a manual gate valve, a pneumatic flow control valve, a pressure-regulating gate valve, and an air-diverter plenum with 12 m3 volume. This plenum is then followed by the test-section segment, an exhaust plenum with a volume of 2 m3, and an exhaust piping system. Figure 1 shows a diagram of the associated wind tunnel leg, which includes the diverter plenum, inlet duct, supersonic nozzle, test section, and exhaust plenum.
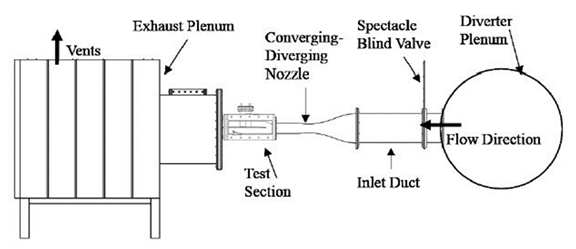 | Figure 1. Schematic diagram of the wind tunnel facility |
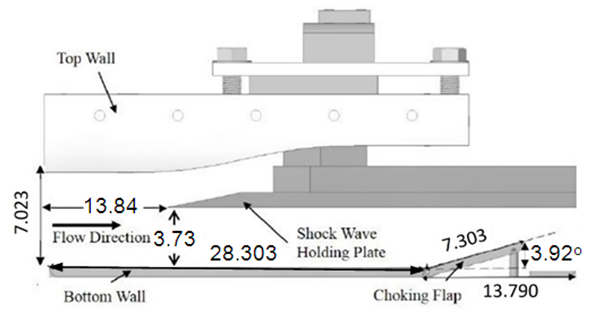 | Figure 2. Schematic diagram of test section. All dimensions are given in cm |
2.2. Overall Data Acquisition and Analysis Procedures
- Phantom Camera Control 2.7 software is employed to process the images which are captured by the Phantom camera. Spatial resolution of each image is 20 micrometers per pixel location. The exposure time is 1.0 μs at all sampling rates which are employed within the present investigation. Digitized shadowgraph visualization images are acquired at a data acquisition rate 10 kHz. Additional data analysis and processing are accomplished using MATLAB version R2019b software. Associated programs are used to track shock wave position variations with time and to quantify grey scale pixel intensity variations with time in flow areas of interest. These analysis steps are followed by calculations to determine distributions of power spectral density (PSD) and magnitude squared coherence (MSC) as they vary with frequency.Ligrani et al. [12] provide additional information on the facility, test section, and data acquisition procedures.
2.3. Power Spectral Density Determination
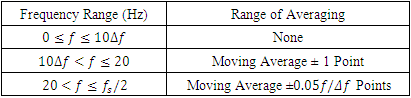
- The first step in the determination of distributions of power spectral density (PSD) with frequency is the application of a 5th order Butterworth filter which attenuates all frequencies above 90 percent of the Nyquist folding frequency. This is accomplished using the butter command within MATLAB version R2019b software. The next step is the application of Welch’s method using the pwelch command within MATLAB to obtain PSD distributions. Each distribution is determined with eight segments and a 50 percent overlapping Hanning data window. The following equation shows how the length of the Hanning window Ls is calculated. Within this equation, L is the total number of measurements and N is the number of window segments.
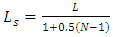 | (1) |
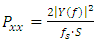 | (2) |
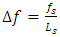 | (3) |
2.4. Magnitude Squared Coherence Determination
- Magnitude squared coherence (MSC) correlation analysis is used to provide information of flow phenomena which are interacting with each other in a coherent manner at different frequencies. The MSC determined value Cxy quantifies the correlation between two datasets, from 0 to 1, as a function of frequency. This analysis is performed using MATLAB with the mscohere function. With this approach, MSC is expressed using an equation of the form
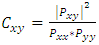 | (4) |
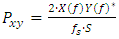 | (5) |
|
3. Statistical Analysis Results
- Within the present investigation, magnitude squared coherence and power spectral density variations with frequency are determined from instantaneous gray scale variations determined from two statistical analysis approaches: tracked instantaneous shock wave motions and from groupings of stationary pixel locations. The tracking approach provides data which are more physically representative of unsteady flow physics. This is because grayscale pixel intensity variations from stationary locations are affected by a shock wave only as it traverses this fixed location. Resulting data then only represent transient and intermittent motion of the shock wave rather than complete unsteady shock wave motion.
3.1. Shock Wave Tracking Determination and Results
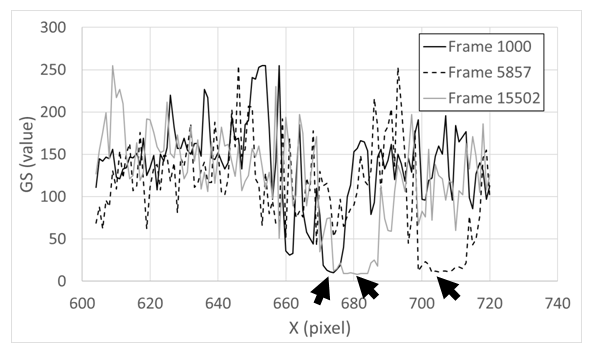
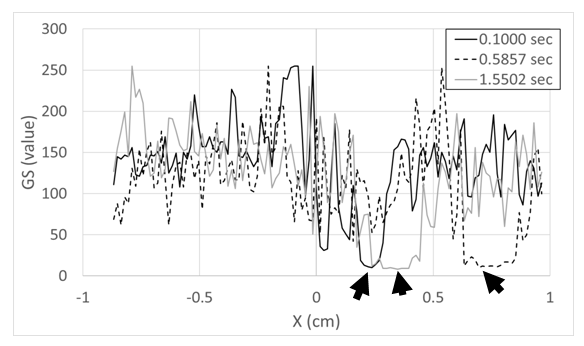
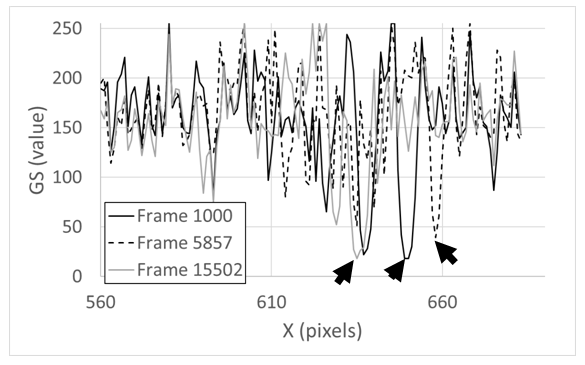
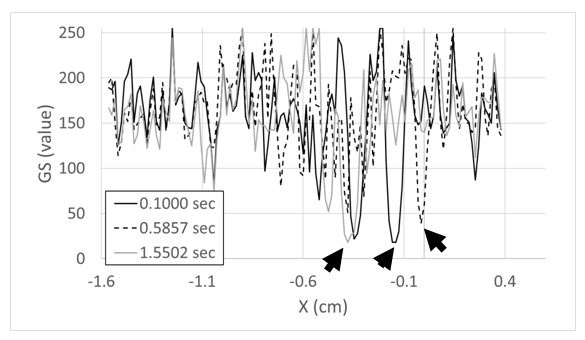
- Shock wave instantaneous locations are tracked along horizontal lines that cross the shock wave. These line placements are solid black and are shown in Figure 3. When the normal shock wave is tracked, the line is located 0.68 cm below the shock-wave-holding plate. When the lambda foot rearward oblique shock wave is tracked, the line is located 2.54 cm below the shock-wave-holding plate. Overall, Figure 3 presents an instantaneous shadowgraph image for one individual digital frame showing different flow phenomena within the test section. Open white squares within this figure denote locations used for stationary analysis using 5 by 5 pixel arrays.
3.2. Power Spectral Density Results
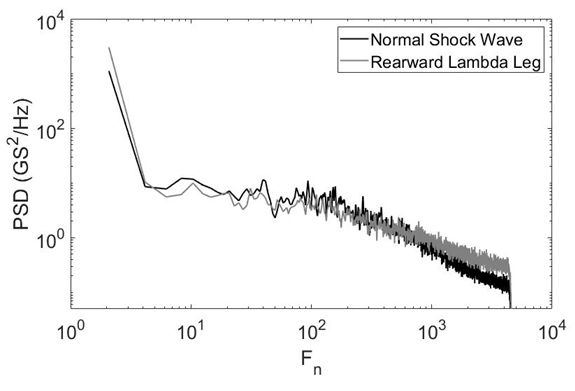
- Power spectral density (PSD) distributions provide estimates of the amount of energy associated with each frequency of the unsteady behavior. Figure 9 shows power spectral density variations with frequency based upon tracked locations of the normal shock wave and the lambda foot rearward oblique shock wave. Overall qualitative variations of the PSD distributions for both the normal shock wave and the rearward lambda shock wave leg have similar shapes, with aligned peaks at 8.5 Hz, 16 Hz, and 25 Hz. In addition, both data sets show a negative slope which indicates a higher energy content associated with larger length scales and lower frequencies. The most important difference between these two data sets in Figure 9 is different quantitative magnitudes at each frequency, with consistently higher values associated with the normal shock wave.
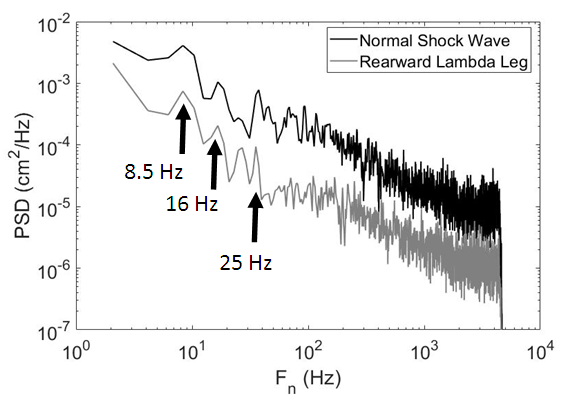 | Figure 9. Power spectral density variations with frequency based upon tracked locations of the normal shock wave and the lambda foot rearward oblique shock wave |
3.3. Magnitude Squared Coherence Results
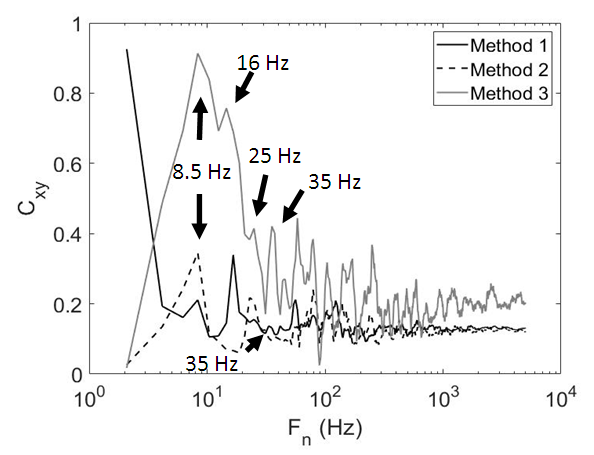
- Figure 11 presents magnitude squared coherence variations with frequency based upon three different analysis approaches, methods 1, 2, and 3. Method 1 is based upon time variations of grey scale pixel intensity value variations within a 5 by 5 pixel region in the vicinity of the normal shock wave and within a 5 by 5 pixel region in the vicinity of the lambda foot rearward oblique shock wave. Method 2 is based upon the tracked time varying position of the normal shock wave and grey scale pixel intensity value variations within a 5 by 5 pixel region in the vicinity of the lambda foot rearward oblique shock wave. Method 3 is based upon tracked locations of both the normal shock wave and the lambda foot rearward oblique shock wave. Within Figure 3, the locations used for stationary analysis with the 5 by 5 pixel arrays are denoted using open white squares. Line locations used for tracking shock wave locations are also shown in Figure 3.The highest coherence values within Figure 11 are produced using method 3. Local maxima peaks for this method are located at 8.5 Hz, 16 Hz, and 25 Hz, which correspond to similar PSD peaks in Figure 9. Within Figure 11, a similar peak at 8.5 Hz is present which is associated with methods 1 and 2, and a peak at 25 Hz is associated with method 2. There is also a very small peak for Method 1 around 35 Hz, whereas with Method 3, a large local maximum is present near the same frequency. This locally high value with method 1 is not present when methods 2 and 3 are employed. This is partially due to methodology for methods 2 and 3 because correlations are determined for spatially tracked streamwise position data relative to an average value which is set equal to zero. This zero value also appears in correlation distributions for frequencies near 0 Hz due to the associated Fourier transform offset. However, this is not the case for method 1 results. The superficially high MSC values at low frequencies for the method 1 results are additionally due to the intermittent motion of the shock waves as they transverse stationary pixel locations.
4. Summary and Conclusions
- Of the different statistical analysis approaches used for magnitude squared coherence determination, method 3, wherein analysis is based upon tracked locations of both the normal shock wave and the lambda foot rearward oblique shock wave, provides the most physically relevant results. This relevancy is demonstrated by the highest coherence values for all frequencies which are provided using method 3, relative to methods 1 and 2. When magnitude squared coherence values are based on grayscale variations from flow phenomena determined at fixed pixel locations, anomalous coherence values are produced due to inappropriate analysis methodologies and because of intermittent motion of the shock waves as they transverse stationary pixel locations. Power spectral density quantitative and qualitative data trends lead to similar conclusions. Illustration is provided by power spectral density variations with frequency which are based upon tracked locations of the normal shock wave and the lambda foot rearward oblique shock wave. Ensemble averaged spectra for these two types of tracked shock waves have peaks which are aligned with each other at frequencies of 8.5 Hz, 16 Hz, and 25 Hz. These peaks are also in excellent agreement with frequencies of local maxima within magnitude squared coherence distributions which are based upon tracked shock wave location analysis.
ACKNOWLEDGEMENTS
- The present research effort was funded by the CBET Thermal Transport Processes Program, National Science Foundation, Award Number 2041618.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML