-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2021; 11(1): 8-11
doi:10.5923/j.statistics.20211101.02
Received: Mar. 2, 2021; Accepted: Apr. 11, 2021; Published: May 15, 2021

A Survey of Infant Mortality and Cost of Living Index of Some Developing Countries
Omobolaji Halid, Tomilola Halid, Anthony Ilesanmi, Modupe Oluwayose
Department of Statistics, Ekiti State University, Ado-Ekiti
Correspondence to: Tomilola Halid, Anthony Ilesanmi, Modupe Oluwayose , Department of Statistics, Ekiti State University, Ado-Ekiti.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This work covered a survey of infant mortality rate and cost of living index of some developing countries. Data of infant mortality rate and corresponding cost of living index of these developing countries was collected for a five year period. The ordinary least squares method was used to fit five functional forms of regression model considered. The comparative suitability of the models for the data was investigated using model diagnostic procedures in order to identify the best model. Results showed that all the models have statistically significant t and F-ratios. The Log-Lin model was adjudged to have the best fit since in addition to its statistical significance, it also resulted in the lowest MSE and the highest coefficient of determination (R2) which all highlighted an overall goodness of fit.
Keywords: Infant Mortality Rate, Cost of living index, Functional forms, Ordinary Least Squares, Goodness of fit
Cite this paper: Omobolaji Halid, Tomilola Halid, Anthony Ilesanmi, Modupe Oluwayose , A Survey of Infant Mortality and Cost of Living Index of Some Developing Countries, International Journal of Statistics and Applications, Vol. 11 No. 1, 2021, pp. 8-11. doi: 10.5923/j.statistics.20211101.02.
Article Outline
1. Introduction
- Infant mortality is the death of children under the age of one year. Infant mortality rate refers to one of the important indices of economic development and social health status of any country. It is considered as the most sensitive measures of mortality. Infant mortality rate can be calculated by the number of deaths of children in a particular region within one year divided by the number of live birth for that region during the same year multiplied by 1000. It is generally classified by neo-natal death (0-28 days) and post natal death (1month - 12 months). Again, the early neo-natal death is known as pre-natal death (0 -1 week). Neonatal deaths are further subdivided into early (first week) and late (second, third and fourth weeks). In prosperous countries, neonatal deaths account for about two–third of infant mortalities. Many studies have showed that death are higher during the first year of live irrespective of whether the overall level of mortality are high or low. [7] found that 57.7 percent of deaths under one year old occur during the first month of their lives. The most important causes of death in neonates were prematurity, low birth weights (44.4%) and later gastroenteritis (30.3%). In addition, narcotic toxics (9.6%) had been identified as another cause of infant mortality.Cost of living is the price of goods and services required for maintaining an average level standard of living. Cost of living varies from time to time. A cost of living index is a theoretical price index that measures relative cost of living overtime or regions. It is an index that measures differences in the price of goods and services, and allows for substitutions with other items as prices vary. Cost of living calculations are also used to compare the cost of maintaining a certain standard of living in different geographic areas. Difference in cost of living between locations can also be measured in terms of purchasing power rate. A developing country is also known as an LMIC, or a low and middle income country. An increase in infant and child mortality rates especially in Africa and other developing nations had been of great interest to many in recent times. Increasing rate of infant mortality in most developing countries had been attributed to mainly poverty resulting from corruption and bad leadership. Some had been attributed to high level of female illiteracy rates. Poor health resulting from pollution, a consequence of oil spillage and industrialization , outbreak of epidemics, limited access to portable water, poor sanitation and waste disposal strategies to mention a few. The study of infant mortality using multiple linear regression and reciprocal regression had been reported in [1] and [2] with some notable results. These studies considered parents’ income and female literacy rates as predictors to child mortality rate. These studies are also limited toonly one country. It is against this background that this work seeks to investigate the influence of living cost index on infant mortality in some selected developing nations of the world. The choice of an appropriate regression model is mandatory for accurate prediction of infant mortality and efficient policy formulation which is why the consideration of different functional forms of regression is required in this work.
2. Materials and Methods
- There exist different functional forms of regression model which are linear in the parameters but not necessarily linear in the variables. Most of these models are usually subjected to appropriate transformation so that they can satisfy the linearity condition in order to allow for the application of ordinary least squares technique. In this work, the reciprocal model, the lin-log model, log-log model, log-lin model and the log-reciprocal regression model were fitted to the data of infant mortality and cost of living index of some selected developing countries using the ordinary least squares technique. The countries considered are Venezuela, Bahamas, Estonia, Malta, Uruguay, Lebanon, Cyrus, Latvia, Costa Rica, Tunisia, Algeria, Ghana, Nigeria, Zimbabwe, Bahrain, Iran, Cambodia, Oman, Panama, Serbia, Kenya, Namibia, Mauritius, Egypt, Ethiopia, Tanzania, Uganda, Libya, South Africa and Morocco. The performance of each of the models was determined via comparison using some model diagnostic procedures and overall goodness of fit measures. This comparison will provide information on the best model for the data. The model with the highest coefficient of determination and overall goodness of fit will be adjudged the best. Data of infant mortality was sourced from UNICEF Global Database while the cost of living index was sourced from www.numbeo.com. The data is a five year data of infant mortality rate and cost of living index collected from for 30 developing countries between 2013 and 2018. All the analysis was carried out using SPSS (version 20.0). Each of the estimated models will be assessed for any problem of econometrics and an appropriate model diagnostic procedure will be used to identify the functional form with best fit.
3. Functional Forms
- The different forms of two-variable regression models which are linear in parameters; not necessarily linear or non-linear in variables considered are the reciprocal, log-linear, lin-log and logarithmic-reciprocal models. They have the particular feature that they can be made linear in parameters by transformation such that the classical linear regression assumption on linearity is satisfied and the ordinary least square method can be used for their estimation. The reciprocal regression model is of the form
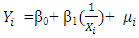 | (1) |
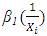 approaches zero, Yi approaches the asymptotic value of β0.Also, of great importance is the logarithmic reciprocal model which has the form
approaches zero, Yi approaches the asymptotic value of β0.Also, of great importance is the logarithmic reciprocal model which has the form 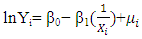 | (2) |
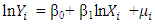 | (3) |
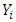 and
and 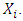 This feature allows for estimation by means of the OLS. (3) is also called the log-log or double log model. It is very popular in applied econometrics.Other functional forms include semi-log model which are of two types; Log-Lin and Lin-Log models. The Log–Lin model is represented by
This feature allows for estimation by means of the OLS. (3) is also called the log-log or double log model. It is very popular in applied econometrics.Other functional forms include semi-log model which are of two types; Log-Lin and Lin-Log models. The Log–Lin model is represented by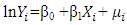 | (4) |
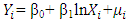 | (5) |
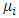 the stochastic disturbance term which is NID i.e.
the stochastic disturbance term which is NID i.e. 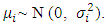 Upon transformation of any of the five forms, one may replace lnXi or
Upon transformation of any of the five forms, one may replace lnXi or 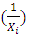 by Xi*, likewise
by Xi*, likewise 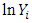 by
by 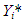 for simplicity so that we have a typical two-variable regression of the form
for simplicity so that we have a typical two-variable regression of the form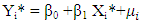 | (6) |
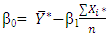 and
and 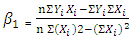 are the parameter estimates.
are the parameter estimates.4. Analysis and Discussion of Results
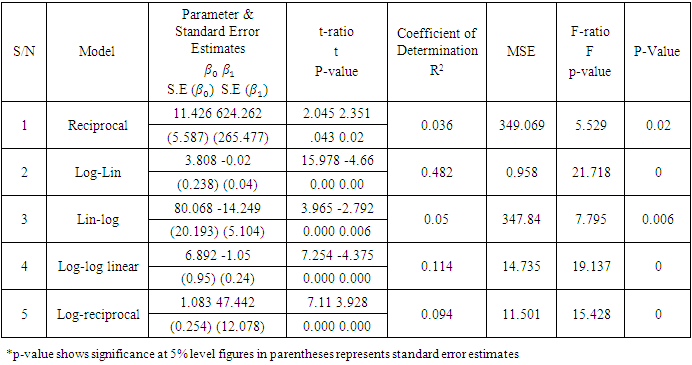
- Data of infant mortality was sourced from UNICEF Global Database while the cost of living index of some developing countries was sourced from www.numbeo.com. The data is a five year data of infant mortality rate and cost of living index of 30 developing countries collected from 2013 to 2017. The models used are five different functional forms of regression model. Their comparative suitability was investigated using some model fit criteria in order to identify the model with the best fit. The five functional forms considered in this work are reciprocal, Log-Lin, Lin-Log, Log-Log and Log-reciprocal models. The ordinary least square method was used to fit the five models to the data where infant mortality rate was the outcome variable (Y) and cost of living index was the predictor(X).The statistical analysis of the data was carried out using SPSS (version 20.0). The analysis will reveal the parameter estimates, standard error estimates (for each parameter), and coefficient of determination, t-ratio and F-ratio as well as MSE of each of the estimated models. The t-ratio, F-ratio, the coefficients of determination, and MSE will provide information on the statistical significance of the parameters (or variables) and (overall) goodness of fit. The model with statistically significant t and F-ratios, highest coefficient of determination and lowest MSE will be adjudged to be the best model.Table 1 is a table of comparison of results of different fitted functional forms of regression models. The comparison of the performance of each of the models was done using the coefficient of determination, mean square error, p-values of the t-ratio (for test of significance of parameters) and F-ratio (test of overall regression.
|
5. Discussion and Conclusions
- The negative sign in the (partial) slope parameter of the estimated Lin-Log, Log-Lin and Log-log models implies that for every unit increase in the cost living index, there will be a decrease in the infant mortality rate. Similarly, the positive signs (and the inverse proportionality between the outcome variable and predictor) in the estimated reciprocal and log-reciprocal models also show that for every increase in the living index, there will be a decrease in the mortality rate. These results, in addition to their statistically significant t-ratio and F-ratio, highlighted overall goodness of fit in all the functional forms considered and made us conclude that each of the models is capable of fitting the data. This is in consonance with the result of [1]. The coefficient of determination for each of the models also highlighted a goodness of fit in each of the models. In fact, the model with the least R2 value of 0.036 indicated that approximately 3.6 percent variation of the cost of living index (of the countries) is explained by variation in infant mortality rates in the model. The Log-Lin model yielded the highest R2 value of 0.492 which clearly means that approximately 50 percent variation in cost of living index is explained by variation in infant mortality rate by the model. In addition to this result, the Log-Lin model yielded the lowest MSE. These lead to the conclusion that the log-Lin model is the best model for the data since it has the lowest mean square error value and the highest R2 value in addition to its statistically significant t and F ratios. A very good model fit usually have R2 value very close to 1 and R2 value may improve with the inclusion of more independent variables. However, a relatively low R2 value does not necessarily imply a bad fit in [4] but the inclusion of other variable (s) in the model, apart from cost of living index, is suggested in order to improve the R2 value. This suggestion may be necessary as literacy rate and poor health resulting from limited access to safe water, outbreak of epidemics, high percentage of people living with infectious diseases, poor sanitation and other hygiene problems as well as pollution may influence infant mortality rate apart from ‘widespread’ poverty in developing countries. How well the latter can be well measured or quantified remains a daunting question because of inadequate information, personnel and adequate technology for monitoring or keeping tab on such statistics in most developing countries.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML