1. Introduction

In plant breeding the genotype-by-environment interactions play important role in developing specifically or broadly adapted genotypes across a wide range of environments. Therefore, the G×E interaction effect should be accounted for in the Bayesian model to predict breeding values [1]. Bayesian statistical analysis assumes that all uncertainty should be shaped with probability and that statistical inferences should be logical decision the laws of probability [2]. Plant breeders evaluate the lines in several locations and years for estimating the genetic performance [3]. Analysis of variance of an estimation of variance components from data arises in many areas of agricultural experimentation, especially in agronomy and plant breeding research. However, Bayesian estimation of variance components in multiple locations and years of balanced dataset has appeared in extremely limited cases [4]. The effects of G×E (genotype x environment) interaction on selection efficiency is negative in the case of qualitative effects (i.e. when G×E interactions change the ranking of genotypes in different environments). When discussing these interactions, it is essential to define whether ‘E’ indicates the year (Y), location (L) or a combination of the two [5]. However, although the breeding consequences of genotype by year (G×Y) interaction (GYI), genotype by location (G×L) interaction (GLI) and genotype by year within a location (GYIwl) interaction are quite different, a large part of the literature on G×E interaction does not make this distinction and, instead, lumps Y and L together as ‘environments’ [6]. Dror and Steinberg has applied Bayesian analysis that exploits a discretization of the parameter space to efficiently represent the posterior distribution [7], Bayesian solutions have been to some decision problems in crop management and variety selected [8]. Orellana used a Bayesian approach to estimate variance components in a hierarchical model under heterogeneous error and GEI variances applied to corn yield data [9]. To understand the criteria breeding strategies, the knowledge of genetic gains and heritability are useful in selection of recommendable features [10]. Omer et al., have stated clearly and in detail the Bayesian estimation of genotype-by-environment interaction in sorghum variety trials when interactions were GxE [4]. Bayesian approach is required a basic strategy to be used for analyzing a multiple environmental trial (METs) data, the good practice of analysis of variance and set out methods of presenting posterior results that comparing with a classical approach [11]. Jiang and Skorupski examined a Bayesian statistic to estimating variance components within a multivariate generalizability theory framework. In most of the METs data are normally tested over a wide range of environments (locations, years, growing seasons, etc.) and reliable statistical information can obtain using ANOVA or linear mixed models [12].

In this study the models will be investigated for partially hierarchical ANOVA for the combined analysis of sets of experiments laid out in randomized complete block designs. In Bayesian approach the standard computational approach is to use Markov chain Monte Carlo (MCMC) methods to draw samples from posterior distributions [13]. Gibbs sampler and Metropolis Hastings algorithm are the two commonly used Markov chain Monte Carlo (MCMC) methods [14]. Application of Bayesian methods for variance component model in agricultural trials were reported by [15]. Luo et al., performed statistical approach of Bayesian inference for genetic parameter estimation of categorical traits of the direct and maternal genetic effects by Gibbs sampling [16]. Recently, Da Silva et al., studies Bayesian methods for Heterogeneity variance component under the additive main effects and multiplicative interaction (AMMI) model for multi environmental trials [17]. Also, Sun et al., has discussed different Bayesian methods for variance component model [18]. Incorporating the prior information of variance components from multi environment trials on the genotypic parameters available from previous similar trials has potential for adding value to the crop breeding program [15]. The variance components will be estimated using the appropriate mixed model structures fitted using experimental design data. To assess the relative contribution of genotype and genotype interactions, we estimated the variance components due to genotype (G), location (L) and two types of interaction: The G×L interaction and the G×Y interaction within location pooled over all the locations [19]. In plant breeding adaptation strategy and yield stability goals, variance components are used for determining most adaptable environment to genotype and genotype ×environment effects. Genotypic variance components for balanced data sets can be estimated as described in the liner mixed model [20]. An estimate of the former is obtained from the variance of the genotypic standard deviation values estimated for individual environments through separate ANOVAs [21].

The motivation for the research work arises from the viewpoint that the selection of an accurate estimate of variance components is particularly important for breeding value in plant breeding programs [22]. In plant breeding the new varieties are grown in several locations and years under different conditions of climate and soil fertility, therefore the different from the environmental conditions contribute to the genetic components of variance [23]. The use of Bayesian approach for estimating of variance components, which deal with unknown distributions for small data sets provide an exact posterior density [24]. The objective of this study is to obtain Bayesian estimates of heritability in broad sense for seed yield, genetic advance due to selection and variance components, when the interactions include (location × variety interaction), (year × variety interaction), (location × year × variety interaction) and the plot errors.

2. Materials and Methods

2.1. Experimental Data

The studied dataset consists of seed yield values in kg/ha on twelve genotypes of chickpea evaluated for three years (2006, 2007 and 2008) at six locations: Delhi, Sriganganagar, Kanpur, Faizabad, Sehore and Junagarh, in India. The experimental design was a randomized complete block with three replications in each location and year. Twelve chickpea genotypes were BG256, DCP92-3, GNG469, HC3, HC1, ICCV10, ICCV2, JG11, JGK1, PantG186, Radhey and RSG 888. The chosen locations represented the chickpea production regions in India.

2.2. Frequentist Approach for Linear Mixed Model

The linear mixed includes model where the three-factor interaction among genotype, year, and location (GYLI) is interpretable. If the test locations are geographically close (e.g., they might be the areas in nearby blocks of the same field) then the constituents of the ‘year’ factor can reasonably be assumed to be nearly the same over all the locations each year. In this case, it is possible to evaluate both the spatial interaction of genotype with location and the temporal interaction of genotype with year. This allows researchers to measure changes in the genotype × location (spatial) interaction in relation to year (time), as well as changes in the genotype × year (temporal) interaction in relation to location (space). ANOVA models as well as the REML models are herein considered for the combined analysis of sets of experiments laid out in randomized complete block designs. The ANOVA models comprise four factors assuming that the location is fixed while replication effects, genotype effect, and all other factor effects are random [25]. The interactions include location × genotype interaction (GLI), year × genotype interaction (GYI), location × year × genotype interaction (GLYI) and the plot errors. The yield response 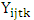is modeled as follows:

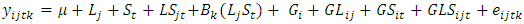(1)

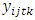Where is the yield response of the genotype i in the location j, year (or season) t and block k; 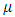= grand mean, 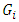is the effect of the genotype i, 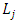is the effect of the location j. 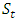is the effect of the year t and 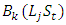is the effect of block k within location (j) and year (t). This model is useful for multiple experiments trials conducted over locations and repeated in different time; with associated subscripts, 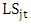is the effect interaction between locations and years, 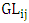is the effect interaction between genotypes and locations, 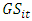is the effect interaction between genotypes and years, 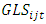is the effect interaction between genotypes, locations and years. 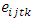is the residual error from the plot for 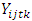, and assumed to be normally distributed with homogeneous variance 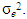It is assumed that 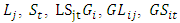and 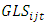are normally and independently distributed, with means zero and variances 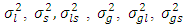and 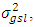respectively. The values of vector indices are 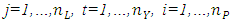and 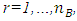where 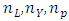and 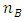are number of locations, years, genotypes and blocks respectively. Bayesian estimation of variance component estimation will be based on the linear mixed model in equation (1). Bayesian approach therefore uses wide- adaptation rather than specific- adaptation where one pools the GY and the GLY interaction components to estimate temporal stability of genotypes [26].

2.3. Bayesian Approach for Linear Mixed Model

In Bayesian application, the observations are assumed to be exchangeable samples (modeled as independent samples from some probability distribution) [27]. Thus, from a normal distribution as follows:

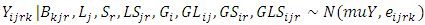where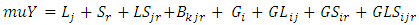

The next level of the Bayesian hierarchy includes prior distributions for location, year, and location parameters (i.e., means) 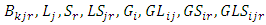and their variances. In REML model all priors distribution were implied as normal distribution with means zero and variances defined to condition the desired level of information sharing among levels of the factor [28]. Independent prior distributions were assigned for the parameters used. These are specified as follows: for block effect = 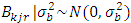, effect of location = 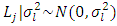, effect of year = 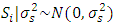, effect of location and year interaction = 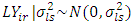, effect of genotypes = 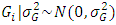, effect of genotypes and location interaction = 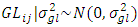, effect of genotypes and year interaction = 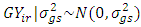, and effect of GLS = 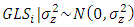. The location factor was argued to be with random effects when the main interest of the analysis lies in the estimation of variance components for locations that are representative of the relevant production area within the target region [29].

2.4. Heritability and Genetic Advance Due to Selection

Heritability plays a vital role in the selection process and measuring the relative influence of environment on the development of a specific quantitative trait [30]. Heritability estimates for phonetic traits are of useful of breeders using to aid in selection decisions [31]. Heritability estimates along with genetic advance is more helpful in foreseeing the genetic gain under selection than heritability estimates alone [32]. Bayesian approach for two types of heritability evaluations for each of the two models will be pursued. Denoting the estimates of genotype, Location and year, Location x year, genotype and year, genotype × Location, year variances by 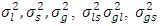and 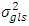and experimental error (environmental) variance by .

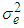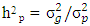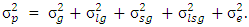In this model the environment E is partitioned as L + S + L x S): Broad sense heritability on a mean-basis where where 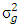is genotypes variance, 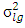is estimate of location by genotypes interaction variance, 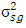is estimate of year by genotypes interaction variance, 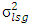is estimate of year x location x genotypes interaction variance, 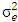is experimental error variance [33], 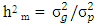where the phenotypic variance,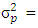 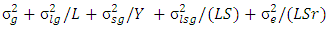Gelman reviewed several options for non-informative priors for scale parameters in hierarchical models and suggested the use of uniform, 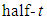and half-normal families of distributions [34]. Crossa et al., used inverse-gamma distribution as a prior for variance components [29]. Based on normal distribution of the trait, the genetic gain due to selection of model, 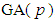, at selection intensity 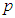is given by

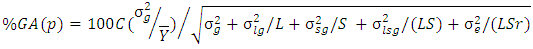where 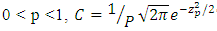The truncation point 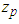in the standard normal distribution is given by the equation 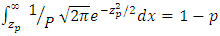where 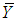is the trial mean. When 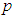= 0.20, 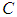= 1.4 [35].

2.5. Priors for the Standard Deviation Components (SDCs)

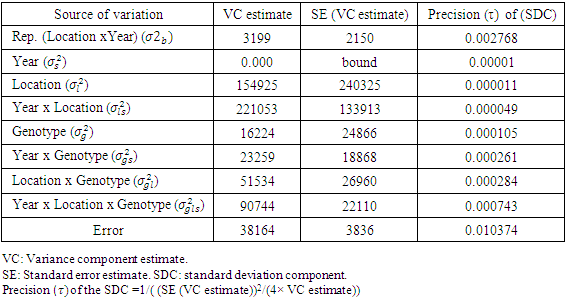
In this study, priors were obtained by using data on seed yield values in kg/ha on 12 genotypes of chickpea evaluated for three years (2006, 2007 and 2008) in different three locations from three different experiments of same genotypes in RCBDs with three replications at Ludhiana, Ranchi and Berhampore in India. The various components of variance were estimated using restricted maximum likelihood (REML) estimation, by taking data from the three years only used as previous data for building prior information. The estimates of variance components along with their standard errors were obtained by using REML and associated directives in the Genstat software. The variance parameters of variance components the SDCs were estimated by using the approximation for variance of square-root of a random variable, say X, as Var(X)/(4X). Table 1 gives the estimates of the variance components and values of the precision parameter 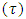of the SDC 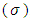, defined as the inverse of its variance. The a priori distribution for the SDC 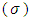, may be denoted as the positively-truncated-normal: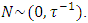

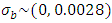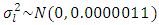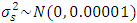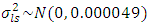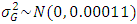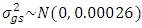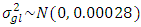Table 1. Estimates of and precision of the standard deviation components from data on seed yield values in kg/ha on 12 genotypes of chickpea at three locations (Ludhiana, Ranchi and Berhampore) in India over three years (2006, 2007 and 2008)

The a-priori distributions of the variance components or, in terms of the scale parameters in several locations and years interaction with the application were taken as uniform, half-t, Gamma and half-normal families of distributions. The priori distributions that have been used for estimation of the variance components, heritability and genetic advance are listed in the following sets of priors:

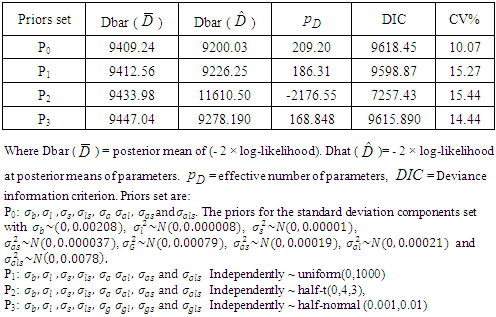
1) P₀: the priors for the standard deviation components set with , , , , , , and .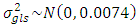

2) P₁: the priors for the standard deviation components 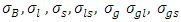and 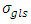follow Uniform (0, 1000),

3) P₂: the priors for the standard deviation components 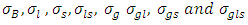follow Half-t distribution 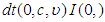= (Half-t (0, 4,3). Here, 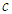is non-centrality parameter and 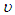is the degree of freedom of the t-distribution. The values of 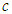and 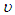are set at 5 and 2 respectively.

4) P₃: the priors for the standard deviation components 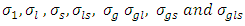follow Half-normal distribution 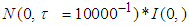= Half- normal (0.001, 0.01)I(0,), 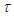is precision parameter, 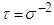given as inverse of variance.

Winbugs and R codes have been presented in a Bayesian framework in appendixes presented in the paper. The example files contents of the WinBUGS and R codes are given in Appendices A1 and A2. The number of iterations was set at 50,000, the number of chains was set at three, and the last 5,000 simulated values of the parameters were taken for evaluating the posterior distributions.

3. Results and Discussion

3.1. Selection of Priors

The standard frequentist analyses components were carried out using ANOVA and REML procedures of Genstat and the various statistics computed are presented along with the statistics using a Bayesian approach. The choices of priors for Bayesian analysis were made from the statistics given in Table 1 in case of all factors being assumed random, when the interactions include (location × variety interaction), (year × variety interaction), (location × year x variety interaction) and the plot errors. The values of DIC and p_D are different for each distribution. However, the prior set P₂ (half-t prior) seems to have a numerically lowest value of DIC (7257.43). We took, P₀ (prior based on similar data distribution taken from a different environment) and P₂ (half-t prior) for further estimation of the model parameters and providing a better understanding on how the parameters mentioned above affect the resulting Bayesian posterior parameters. Results of heritability, genetic advance and variance components of all factors are shown in Table 3 and Table 4, which provides a general picture of the relative magnitudes of the effects of genotype, location, year, and the genotype by location interaction due to genotype + location + genotype by location variations. Location was the most important source of yield.

Table 2. DIC values for selection of the priors for seed yield RCBD (2006 – 2008), India on Chickpea datasets

Table 3. Frequentist estimates and Bayesian posterior means of error variances, genotypic variance, phenotypic variance, heritability, and genetic gain for chickpea seed yield from the trials in 18 environments (2006 – 2008), at (Delhi, Sriganganagar, Kanpur, Faizabad, Sehore and Junagarh) in India based on half-normal prior using previous data

Table 4. Frequentist estimates and Bayesian posterior means of error variances, genotypic variance, phenotypic variance, heritability and genetic gain for chickpea seed yield from the trials in 18 environments (2006 – 2008) at (Delhi, Sriganganagar, Kanpur, Faizabad, Sehore and Junagarh) in India based on half-t-prior

3.2. Bayesian Estimation of Posterior Means, Genotypes Variance, Heritability, and Genetic Gain

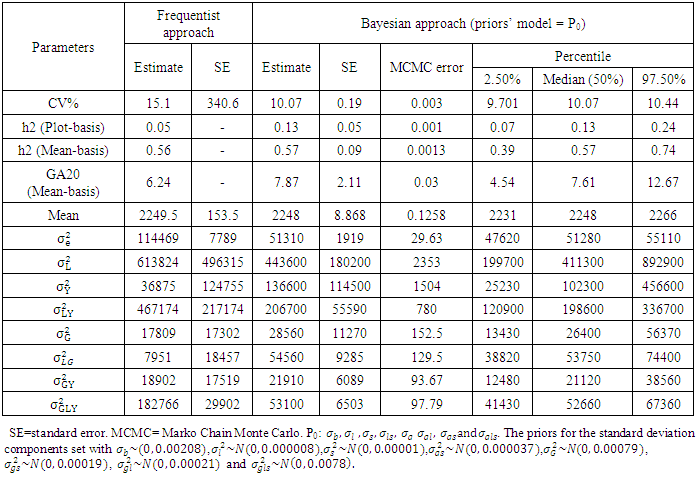
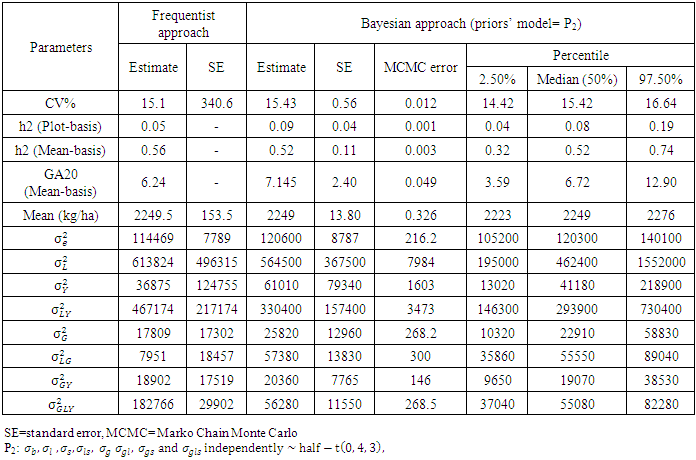
The mean squares of the analysis of variance, heritability and genetic advance both in broad sense, estimation of variance under frequentists and Bayesian approach, as shown in Table 3 revealed significant and highly significant differences for frequentists and Bayesian approaches for heritability both in plot basis and mean basis, it was found to be high in majority cases indicated higher importance of genetic effects in control of traits. Bayesian estimate of experimental error variance 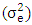or posterior expected value of the error variance given the plot-wise response data under the assumed linear model and half-normal prior (P₀) slightly lower than the frequentists approach, and experimental error variance using half-t prior (P₂) is slightly higher than the frequentists approach or classical least-square estimate. Bayesian estimate of heritability in compare to frequentist approach based on mean basis were (0.52 vs. 0.56) for P₂ and (0.57 vs0.56) for P₀. Bayesian estimate of heritability in compare to frequentist approach based on plot basis were (0.09 vs. 0.05) for P₂ and (0.14 vs0.05) for P₀. Bayesian estimate of genetic advance in compare to frequentist approach based on mean-basis were (7.2 vs 6.2) for P₂ and (7.9 vs. 6.2) for P₀. Half- normal distribution ((P₀) given lowest CV% was 10.6 in comparing with a half-t prior and classical approach were (15.1) and (15.44) respectively. The CV% estimate based on mean value under frequentist and Bayesian approach was quite different, thus, indicating reliable numerical approximation through the number of simulations runs used. In other words, coefficients of variation for each prior are different to each other, indicating a major part of phenotypic variations belonging to genotypic variation (Table 2). The Bayesian estimate of experimental error variance based on mean value using P₀ is slightly lower than that under the Frequentist approach were (51310 vs. 114469), in percentage (31% vs. 69%). The Bayesian estimate of the environment (location × variety interaction) based on mean value were (54560 vs.7951) or in percentage (87% vs. 13%) using P₀ and were (57380 vs.7951) or in percentage (88% vs. 12%) using P₂ are higher than that under the frequentist approach. The Bayesian estimate of the environment (year ×location interaction) based on mean value were (206700 vs.467174) or in percentage (31% vs. 69%) using P₀ and were (330400 vs. 467174) or in percentage (41% vs. 59%) using P₂ are higher than that under the frequentist approach. Bayesian estimate of variance components of all parameters include (year × location interaction), (location × year × variety interaction) and the plot errors are very smallest in comparison to the frequentist approach. While Bayesian estimate of variance components of all parameters include (genotypes, year × genotype interaction, location × variety interaction based on plot are very higher in comparison to the frequentist approach. Bayesian estimates of heritability and genetic advance under two approaches are more efficient; however, Bayesian approach provided confidence interval. Bayesian heritability and genetic advance estimates have been found to be useful in indicating the relative values of selection based on phenotypic expression of different characters. The Monte Carole error in all the parameters of Table 3 and Table 4 are small, indicating reliable numerical approximation through the number of simulations runs used. The distribution of variance components and heritability from Bayesian approach are skewed reflecting a remarkable difference between their means and their variances in both models. It was found that the posterior mean (i.e., the Bayesian estimates) was higher than the corresponding frequentist estimates for heritability and genetic advance. For all the estimates, the posterior standard deviations in the Bayesian approach were smaller than the corresponding standard errors in the frequentist approach.

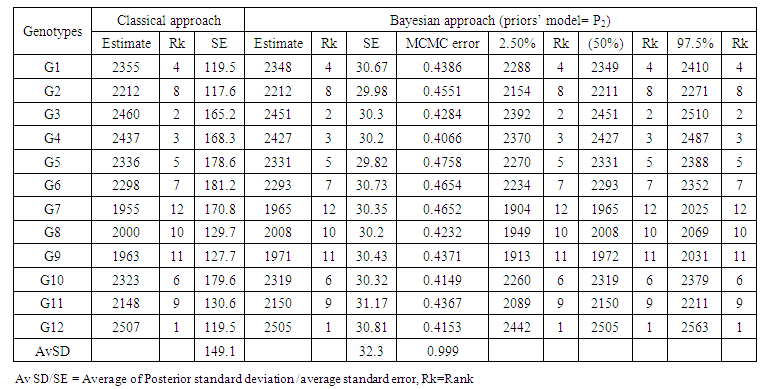Table 5. Predicted values of the genotypes under classical model and Bayesian approach for chickpea for seed yield from the trials in 18 environments (2006 – 2008), at (Delhi, Sriganganagar, Kanpur, Faizabad, Sehore and Junagarh) in India based on half-t-prior

Table 3 comparing the predicted means of the genotypes of frequentist approach using REML estimates and Bayesian approach based on the rankings of the genotypic effects. Correlation between the mean predicted values under the two approaches were 0.99 at (P<0.0001), therefore, the predicted means of the genotypes was the same under frequentist (i.e. classical approach) and Bayesian approach. Bayesian approach indicate that the model was significantly different from each other, providing evidence for Bayesian analysis adequate amount of genetic variability in plant breeding, the genotypes were significantly different in both models. Bayesian heritability estimates were higher compared to that of frequentist approach. It is necessary to identify the components that create the phonotypical difference to calculate the genetic variability and heritability based on that variation fewer than two approaches. Comparison between broad sense heritability revealed equal importance of additive and non-additive effects in genetic control of characters that there is little experimental evidence about whether component of variance calculated from separate analysis of variance in waterlogged conditions is effective in estimating the extent of heritable variation and the effectiveness of selection. The selected sets under ranks of a higher genotypic effect in both approaches were the same, this means that the use of the Bayesian approach led to ideal select of different genotypes and the accurate resulted depends on small variance complements. Generally, Bayesian analysis could be useful in selection procedure in early segregating generations based on genetic advance and would be successful for breeding program to new direction and optional method for explanation.

4. Conclusions

In this paper, we navigated the Bayesian approach for statistical analysis of multi-environmental trials (MET) and compared with the commonly used frequentist approach (i.e., classical approach) The discrepancy information criteria (DIC) were used to identify the most appropriate prior models for applying the Bayesian approach on seed yield data from multi-year and location chickpea trials in Indian environments. The posterior means (i.e., the Bayesian estimates) for variance components for genotype, year, location, and their interactions were substantially lower than those of the respective estimates under frequentist approach, and the associated standard deviations of those estimates were also relatively low under the Bayesian approach. In general, Bayesian estimates of the coefficient of variation were found smaller than those under the frequentist approach. Bayesian estimates of heritability and genetic advance were substantially higher than those of the frequentist approach, although the former approach allows a greater number of parameters to be random. This reflects a desirable aspect of Bayesian approach for estimation of genetic parameters in plant breeding in multi environments trials. Both approaches showed less difference in the estimates of genotypic and phenotypic variance, and higher genotypic values compared to environmental variances. The Bayesian codes in WinBUGS of the variance components, heritability, and genetic improvement of multi environmental trails are given for analysis of similar experimental designs in crop variety trials.

ACKNOWLEDGEMENTS

The first author is grateful to ICARDA and Arab Fund for Economic and Social Development (AFESD) for granting a Fellowship for carrying out the research study.

Appendixes

Appendix-A1. WinBUGS Code for Bayesian analysis of variance components, heritability and genetic ddvanceconducted over several locations and years of model1

Appendix-A2. RCode for Bayesian analysis of variance components, heritability and genetic ddvanceconducted over several locations and years