-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2020; 10(3): 55-59
doi:10.5923/j.statistics.20201003.01

Selecting the Method to Overcome Partial and Full Multicollinearity in Binary Logistic Model
N. Herawati, K. Nisa, Nusyirwan
Department of Mathematics, Faculty of Mathematics and Natural Sciences, University of Lampung, Bandar Lampung, Indonesia
Correspondence to: K. Nisa, Department of Mathematics, Faculty of Mathematics and Natural Sciences, University of Lampung, Bandar Lampung, Indonesia.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The aim of our study is to select the best method for overcoming partial and full multicollinearity in binary logistic model for different sample sizes. Logistic ridge regression (LRR), least absolute shrinkage and selection operator (LASSO) and principal component logistic regression (PCLR) compared to maximum likelihood estimator (MLE) using simulation data with different level of multicollinearity and different sample sizes (n=20, 50, 100, 200). The best method is chosen based on mean square error (MSE) values and the best model is characterized by AIC value. The results show that LRR, LASSO and PCLR surpass MLE in overcoming partial and full multicollinearity in binary logistic model. PCLR exceeds LRR and LASSO when full multicollinearity occurs in binary logistic model but LASSO and LRR are better used when partial multicollinearity exists in the model.
Keywords: Binary logistic model, Multicollinearity, LRR, LASSO, PCLR
Cite this paper: N. Herawati, K. Nisa, Nusyirwan, Selecting the Method to Overcome Partial and Full Multicollinearity in Binary Logistic Model, International Journal of Statistics and Applications, Vol. 10 No. 3, 2020, pp. 55-59. doi: 10.5923/j.statistics.20201003.01.
Article Outline
1. Introduction
- Consider that the model has the form
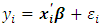 where
where 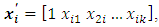
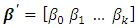 and dependent variables
and dependent variables 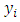 has value either 0 or 1. Estimating parameters in this model where the response variable is binary or multinomial is not appropriate when using the linear regression model estimation method. The linear regression model is based on a ratio scale measurement [1,2,3]. In this case logistic regression model is more suitable.Logistic regression model is based on a logistic function to model binary dependent variables. It is a classification of individuals in different groups. Unlike multiple regression, logistic regression is much more flexible in terms of basic assumptions to be met. Logistic regression model as one of nonlinear regression model does not require liner relationship between independent and dependent variables, assumption of normal distribution and homoscedasticity in the error terms. Despite all the flexibility, the logistic regression model still requires no correlation between independent variables [4,5]. When there is a correlation between the independent variable, logistic model becomes unstable. This can cause errors in the interpretation of the relationship between the dependent and each independent variable in terms of odds ratios [6,7].There are several methods for overcoming the problem of multicollinearity in the logistic models and have been examined by several researchers [8,9,10,11,12]. In this research, a selection of LRR, LASSO and PCLR methods was conducted in logistic model with binary responses and a set of continuous predictor variables. Each method was compared using simulation data that contains partial and full multicollinearity with different sample sizes. The best method was examined based on the minimum value of MSE and the best model is characterized by AIC value.
has value either 0 or 1. Estimating parameters in this model where the response variable is binary or multinomial is not appropriate when using the linear regression model estimation method. The linear regression model is based on a ratio scale measurement [1,2,3]. In this case logistic regression model is more suitable.Logistic regression model is based on a logistic function to model binary dependent variables. It is a classification of individuals in different groups. Unlike multiple regression, logistic regression is much more flexible in terms of basic assumptions to be met. Logistic regression model as one of nonlinear regression model does not require liner relationship between independent and dependent variables, assumption of normal distribution and homoscedasticity in the error terms. Despite all the flexibility, the logistic regression model still requires no correlation between independent variables [4,5]. When there is a correlation between the independent variable, logistic model becomes unstable. This can cause errors in the interpretation of the relationship between the dependent and each independent variable in terms of odds ratios [6,7].There are several methods for overcoming the problem of multicollinearity in the logistic models and have been examined by several researchers [8,9,10,11,12]. In this research, a selection of LRR, LASSO and PCLR methods was conducted in logistic model with binary responses and a set of continuous predictor variables. Each method was compared using simulation data that contains partial and full multicollinearity with different sample sizes. The best method was examined based on the minimum value of MSE and the best model is characterized by AIC value. 2. Logistic Regression Model
- Suppose the response variable of regression application of interest has two possible outcomes or Yi is a Bernoulli random variable with the probability distribution
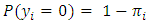 and
and 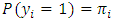 The probability function for each observation is
The probability function for each observation is 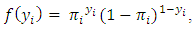 i=1,2,…,n [4,5,6,7]. The multiple logistic regression model of the response variable
i=1,2,…,n [4,5,6,7]. The multiple logistic regression model of the response variable 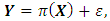 with
with 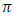 (X) is an n x 1 vector and
(X) is an n x 1 vector and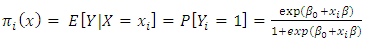 | (1) |
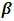 is a
is a 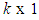 vector of estimated parameters. The logit function of
vector of estimated parameters. The logit function of 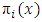 is
is 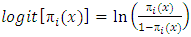 or in linear form can be written as [3,13]:
or in linear form can be written as [3,13]: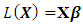 | (2) |
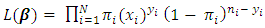 . When the log-likelihood is differentiated with respect to
. When the log-likelihood is differentiated with respect to 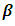 equal to zero, we get
equal to zero, we get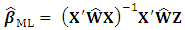 | (3) |
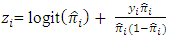 and
and 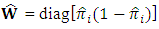 [7].
[7]. 2.1. Logistic Ridge Regression (LRR)
- When multicollinearity exist between independent variables in the logistic model, the matrix X’WX is (near) singular. Using maximum likelihood method to estimate the parameters in the model is not suitable because we cannot get the inversion of the matrix. As a result, the estimation of the parameters in the logistic model using maximum likelihood method is being unstable and cannot be uniquely estimated. In this situation, the ridge regression method can be applied by using a penalty to the diagonal matrix of X’WX to stabilize the coefficients estimates [14,15,16]. Although this method will produce a bias in the coefficient estimates of the model, it provides a lower variance of the coefficient estimates than the unpenalized model. Ridge likelihood estimator of the logistic model is done by maximize the ridge penalized loglikelihood [17,18,19,20,21]:
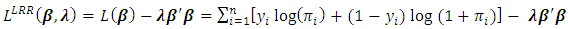 | (4) |
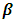 ) with
) with 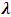 as penalty parameter. Because the value of the
as penalty parameter. Because the value of the 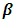 equation is not linear, Newton-Raphson method is used to solve it. The solution uses and follows the iterative weighted least square algorithm to obtained the
equation is not linear, Newton-Raphson method is used to solve it. The solution uses and follows the iterative weighted least square algorithm to obtained the 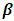 estimates. The logistic ridge regression (LRR) model following [17] is:
estimates. The logistic ridge regression (LRR) model following [17] is: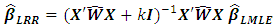 | (5) |
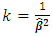 5 and
5 and 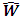 as in equation (3) [17].
as in equation (3) [17].2.2. Least Absolute Shrinkage and Selection Operator (LASSO)
- LASSO method can be used to overcome problems in multicollinearity [22]. LASSO shrinks the coefficient parameter β which correlates to exactly zero or close to zero [23]. Lagrangian constraint (L1-norm) can be combined in a log-likelihood parameter estimation in logistic regression [24,25]. The estimation of parameters in LASSO in combining log-likelihood and Lagrangian constraints produces:
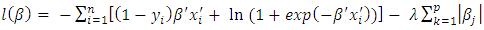 | (6) |
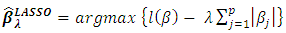 | (7) |
2.3. Principal Component Logistic Regression (PCLR)
- In linear regression analysis, principal component regression (PCR) is one of the methods that has been confirmed to be able to overcome the problem of multicollinearity [1,11,26,27]. PCR aims to simplify the observed variables by reducing the dimensions, where the chosen principal components must maintain as much diversity as possible. This is done by eliminating the correlation between the independent variables through the transformation of the original independent variable into a new variable that does not correlate at all. In terms of the principal component (PC) of the predictor variables, the logit transformation (2) can be written as principal component regression form as:
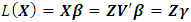 | (8) |
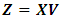 as an n x k matrix whose columns are the PCs of X with V is a k x k matrix whose columns are the eigenvectors of the of the matrix X’X denoted by
as an n x k matrix whose columns are the PCs of X with V is a k x k matrix whose columns are the eigenvectors of the of the matrix X’X denoted by 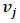 with
with 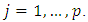 It is obvious that
It is obvious that 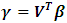 can be estimated by
can be estimated by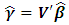 | (9) |
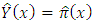 with
with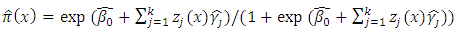 where
where 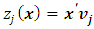 is the j-th PC value for a point x. The logit model (8) can be expressed as
is the j-th PC value for a point x. The logit model (8) can be expressed as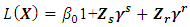 | (10) |
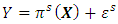 and the logit transformation,
and the logit transformation, 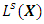 has components
has components 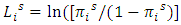 is defined as
is defined as 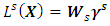 . The parameter estimate of the PCLR [9] is:
. The parameter estimate of the PCLR [9] is: 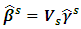 | (11) |
3. Methods
- Illustration of the performance of LRR, LASSO PCLR methods used in this study was carried out using a simulation study to show how these methods can improve the estimation of parameters of the binary logistic model contains partial and full multicollinearity using R. Six independent variables (p=6) were generated using the formula
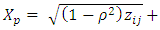
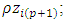
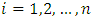 and
and 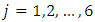 with
with 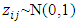 and
and 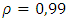 . The dependent variable Y is generated by the binary logistic regression probability
. The dependent variable Y is generated by the binary logistic regression probability 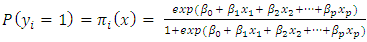 with
with 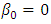 and
and 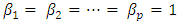 respectively. Partial and full multicollinearity between independent variables were applied in the model with different sample sizes (n=20, 40, 60, 100, 200) and replicated 1000 times. Multicollinearity of the independent variables is measured by
respectively. Partial and full multicollinearity between independent variables were applied in the model with different sample sizes (n=20, 40, 60, 100, 200) and replicated 1000 times. Multicollinearity of the independent variables is measured by 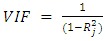 with
with 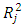 is the coefficient of determination. The best method in estimating the parameters is evaluated using MSE with formula:
is the coefficient of determination. The best method in estimating the parameters is evaluated using MSE with formula: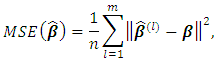 and the best model is characterized by
and the best model is characterized by 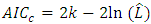 where
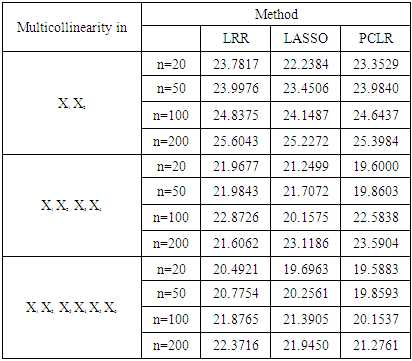
where 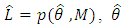 is the value that maximize the likelihood function, n is the number of recorded measurements and k is the number of parameters estimated [28,29].
is the value that maximize the likelihood function, n is the number of recorded measurements and k is the number of parameters estimated [28,29].4. Results and Discussion
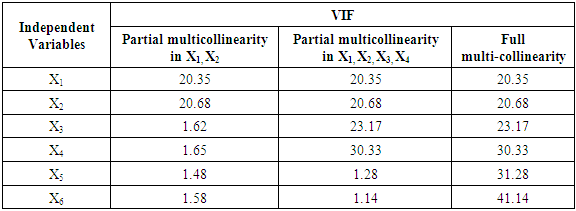
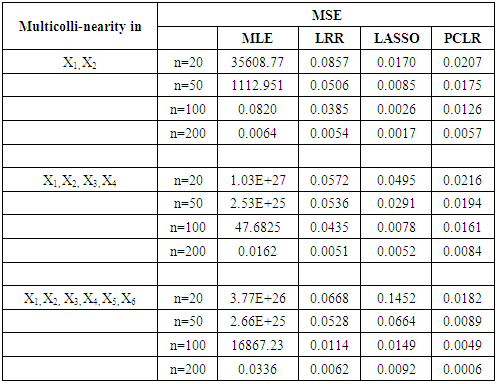
- The partial and full multicollinearity of the independent variables applied in this study is shown in Table 1. First, partial multicollinearity in which correlation only applies between X1 and X2; second, partial multicollinearity where correlation occurs only between X1, X2, and X3; third, full multicollinearity in all independent variables. This condition is applied to all sample sizes that are being studied.
|
|
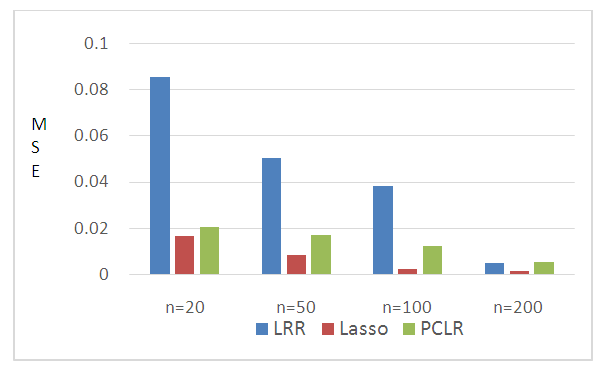 | Figure 1. MSE of partial multicollinearity in X1, X2 |
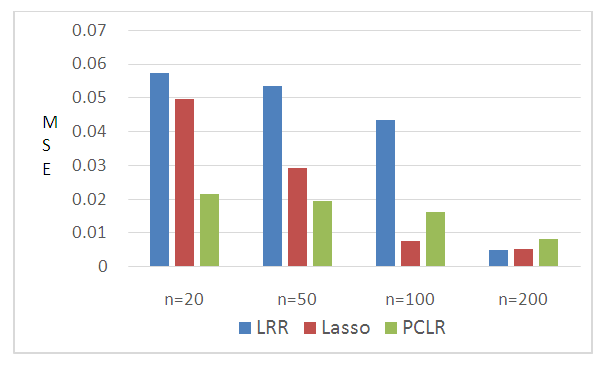 | Figure 2. MSE of Partial multicollinearity in X1, X2, X3, X4 |
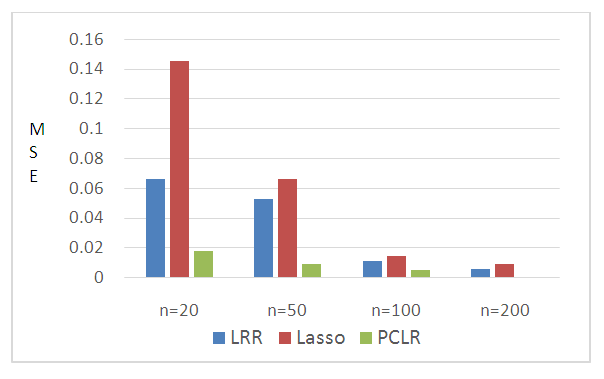 | Figure 3. MSE of full multicollinearity |
|
5. Conclusions
- We conclude from the results of this study that LRR, LASSO and PCLR surpass MLE in overcoming partial multicollinearity and full multicollinearity occur in binary logistic model. PCLR exceeds LRR and LASSO when full multicollinearity occurs in binary logistic model but LASSO and LRR are better used when partial multicollinearity exists in the model.
ACKNOWLEDGEMENTS
- This study was financially supported by University of Lampung. The authors thank the Rector and the Institute of Research and Community Service for their support and assistance.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML