1. Introduction

Univariate models are insufficient to explain random phenomena. Today, data such as drought, wind speed and rainfall are measured together with the variables that may affect them. With the development of technology, the construction of continuous bivariate distribution functions with given marginals has become an importance. When creating new bivariate distributions, models that can express high correlation are generally tried to be obtained. [2] introduced a method which based on the choice of pairs of order statistics of the marginal distributions. [8] studied on construction of continuous bivariate distributions that possesses the Positive Quadrant Dependence property. [13] introduced a generalization of Farlie-Gumbel-Morgentern (FGM) distribution family. They extend the maximal correlation coefficient for FGM family. Furthermore, [14] introduced bivariate and multivariate generalization of quadratic transmutation distribution family. Proposal of [14] draws our attention in particular. Because the transition from univariate case to bivariate or multivariate cases is not so easy. While in univariate case the real line is the complement of the probabilities, at least in the bivariate case these supplements are on the quadrant. There are some issues to overcome for the case of positive values of the transmutation parameter. However, marginals of this model are univariate transmuted distributions and it cannot detect independency. They proposed quadratic rank transmuted bivariate distribution as 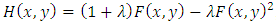, where 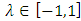. Here, for 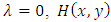gives the base distribution 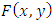. However, if the base distribution is taken from independency case, i.e., 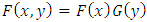, then 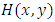can be written as in the eq. (2) of [8] follows: 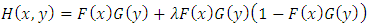. For 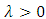, 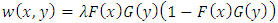cannot meet the conditions (4) and (5) proposed by [8]. Inspired by these studies, the contribution of the article is to propose a simpler but more useful model than the model introduced by [14]. Proposed model also includes both positive and negative values of the parameter as in FGM. Thus, the model gains some flexibility in modeling both positive and negative dependence. Furthermore, proposed model can detect independency. After giving the necessary conditions to construct a new distribution, Spearman's rank correlation coefficient is calculated on two illustrative examples and the usefulness of this family is discussed. Furthermore, some reliability properties are studied for this family.

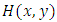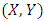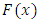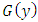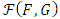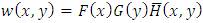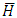Let denote the bivariate distribution function of having continuous marginal cdfs and . Also, let be the distribution family where the respective marginal are F and G. Then, according to the eq. (2) and the condition (3) of [8], we have the function where denotes survival function. This function meets the conditions (3)-(5) given by [8]. Hence, first mixture component distribution is 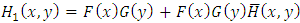. Similar work of [8] given by [15] introduces some conditions for negatively dependent families. According to the eq. (2.1) and the condition (2.1) of [15], we have 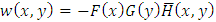. Except for the condition (2.3) of [15], this function meets the conditions (2.2) and (2.4) given by [15]. Distribution properties for the second mixture component 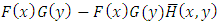have not yet been provided. To overcome this issue, we have the following theorem.

Theorem 1. Let 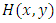be a distribution function belongs to the distribution family 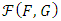which is differentiable on 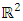and 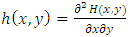denote the joint probability density function. Then

(i) 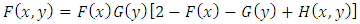is a distribution function,

(ii) 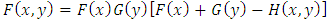is a distribution function if , .

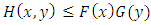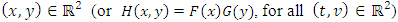Proof. (i) Multivariate distribution function must satisfy following properties:

(P1)

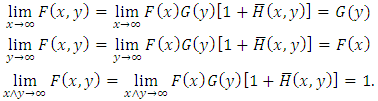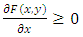(P2) and 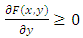. For the simplicity 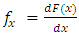and

.

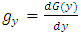
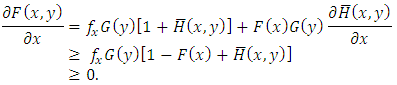Obviously, .

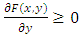(P3) 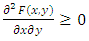. For the simplicity, let 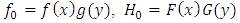and 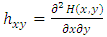. Then

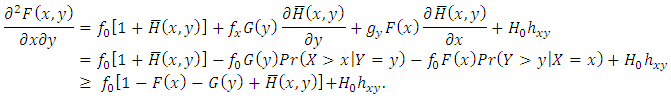Now, by noting that positively dependence implies 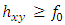, then we have .

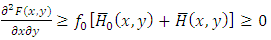Also, negatively dependence implies both 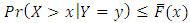and 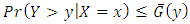. Hence, we have

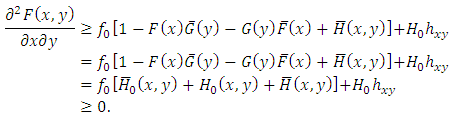(ii) According to [4], Additionally to the properties (P1)-(P3), to determine bivariate distribution uniquely by its marginals bivariate distribution must lie upper and lower Fréchet bounds. Therefore, this idea explains why we need negative dependence for the construction of distribution given in (ii).

(P1)

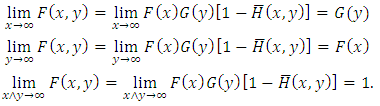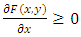(P2) and .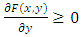

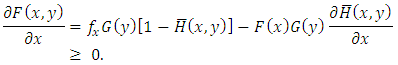Obviously, .

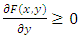(P3) .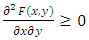

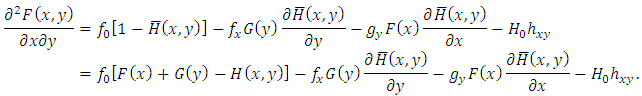Negatively dependence implies 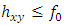. Hence, we have

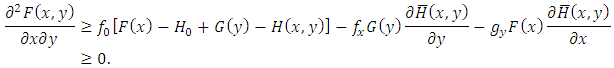However, if X and Y are positively dependent, 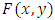can not bigger than Fréchet lower bound. Therefore, the assumption of negative dependence is needed. To show this situation, we assume 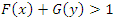. Then we have

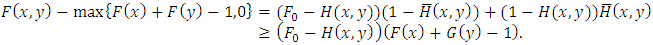As it can be seen that positivity of the above statement depends on .

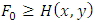According to Theorem 1, first mixture component distribution can be positively, negatively dependent or independent. But the second component distribution must be negatively dependent or independent. Thus, for the base distribution 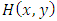, in order to be same structure for both mixture components, the random variables X and Y must be negatively dependent or independent. After this motivation, we can now propose the mixing of these two distributions as follows:

Let T and V be negatively dependent (or independent) continuous random variables. Then their joint distribution function denoted as 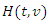belongs to the distribution family 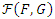where F and G denote respectively marginals of T and V. Let 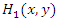and 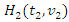respectively denote the distribution functions of 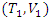and 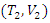having the same marginals as H. The distribution functions of 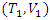and 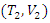are respectively defined by

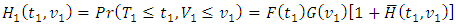(1)

and

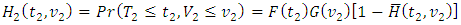(2)

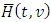where denotes survival function of 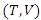i.e., 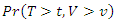. As can be seen immediately from equations (1) and (2), 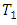and 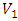are positively dependent random pairs, an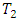d and 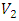are negatively dependent random pairs.

According to Therorem 1, we can define a new pairs of random variables X and Y as below:

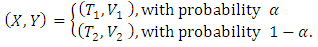Hence, the distribution of 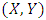obtained by mixing (1) and (2) which is given by

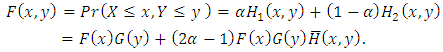(3)

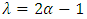By letting , where 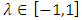, eq. (3) can be rewritten as

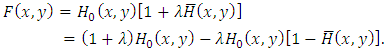(4)

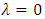indicates 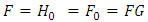i.e., independence of X and Y, 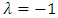indicates that X and Y negatively dependent, and 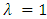indicates positive dependence between X and Y. Note that X and Y are independent from each other, F indicates well-known bivariate distribution which is Farlie-Gumbel-Morgenstern distribution (see, [3] and [5]).

We need the survival and probability density function for subsequent discussions. These functions are respectively given by

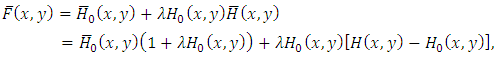and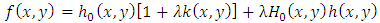

where .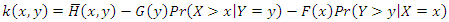

2. Reversed Hazard Rate of the New Family of Bivariate Distribution

The bivariate reversed hazard is defined by [1] as 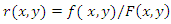. Analogously to the hazard gradient by [7], [11] defined the bivariate reversed hazard rate as follows: 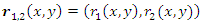, where

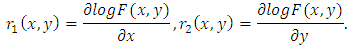Reversed hazard rate gradients of 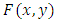given by eq. (4) are as follows:

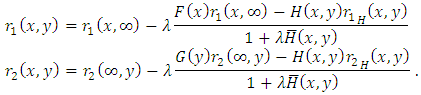Accordingly, after some simplifications, bivariate reversed hazard rate can be given by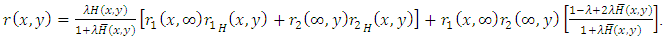

3. Lower and Upper Bounds on Spearman’s Rho Measure for the New Family of Bivariate Distribution

This section deals with obtaining bounds for the bivariate distribution family given by the eq. (4). According to [6] and [4], for any bivariate distribution belonging to 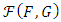contains Fréchet a lower bound and an upper bound. These bounds are respectively defined as

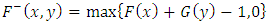(5)

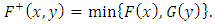(6)

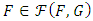For , Spearman’s rho can be expressed as

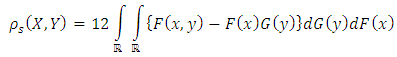(7)

(see, [12]). The coefficient of Spearman’s rho for the new family can be obtained by

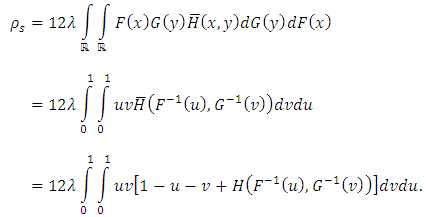(8)

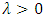Hence, by using the eq. (5) for , we have the lower bound as

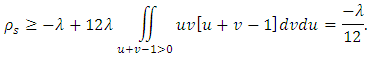To obtain the upper bound, we use the eq. (6), then

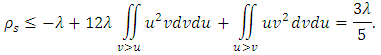According to sign of 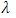, we achieve the bounds as below:

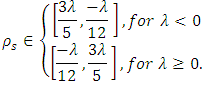We have two example to illustrate this family.

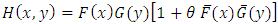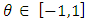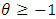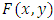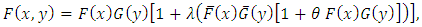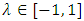Example 1. The Farlie-Gumbel-Morgenstern (FGM) family of bivariate distributions are given by , for . By taking , the distribution is given by where and 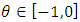. Hence, 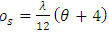. Since 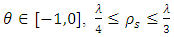. One can conclude that this family model weak dependence as FGM does.

Example 2. The bivariate Gumbel- Exponential (BGE) distribution is given by 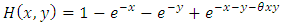, for 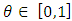. The distribution 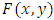is given by 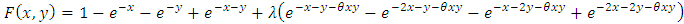, where 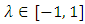and 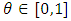. According to [9], the Spearman’s rho coefficient of BGE distribution is 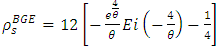, where is the exponential integral function. After some algebraic manipulation, 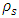can be obtained as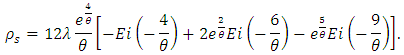

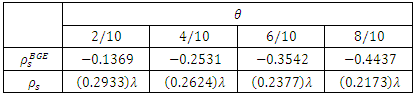
We calculate approximates values of 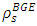and 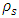by using Maple with respect to some values of 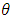. Tabulated values are given as Table 1 below:

Table 1. Approximate Values of Spearman's Rho for BGE and F

For the proposed bivariate distribution families, it is generally expected to model a stronger correlation structure between two random variables. The distribution derived from the base of FGM can only reach the correlation structure that FGM can model. But, unlike in Example 1, as can be seen from the Table 1, it can be said that F can model negative dependence slightly better than BGE in small theta values. Then, we can choose this distribution as an alternative to BGE to provide a correlation structure between random variables.

4. Conclusions

In this study, we proposed a new bivariate distribution using a base distribution from the negative dependency class which is in 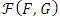. Thus, this new distribution can reveal both negative dependence, positive dependence and independence between the random variables X and Y. The upper and lower bounds show that the values of the correlation coefficient for this family lies in the interval 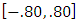. Besides, as a result of illustrative examples, it can be said that distributions can be derived for pairs of random variables with higher correlations considering some base distributions. For further discussion, focusing on the negative dependence condition on 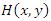, a new distribution family can be derived with any distribution function from .

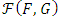ACKNOWLEDGEMENTS

We thank anonymous referees for their valuable suggestions and constructive comments which helped us in revising the paper in the present form.