-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2019; 9(4): 101-110
doi:10.5923/j.statistics.20190904.01

Second Order Regression with Two Predictor Variables Centered on Mean in an Ill Conditioned Model
Ijomah Maxwell Azubuike
Department of Maths/Statistics, University of Port Harcourt, Nigeria
Correspondence to: Ijomah Maxwell Azubuike, Department of Maths/Statistics, University of Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

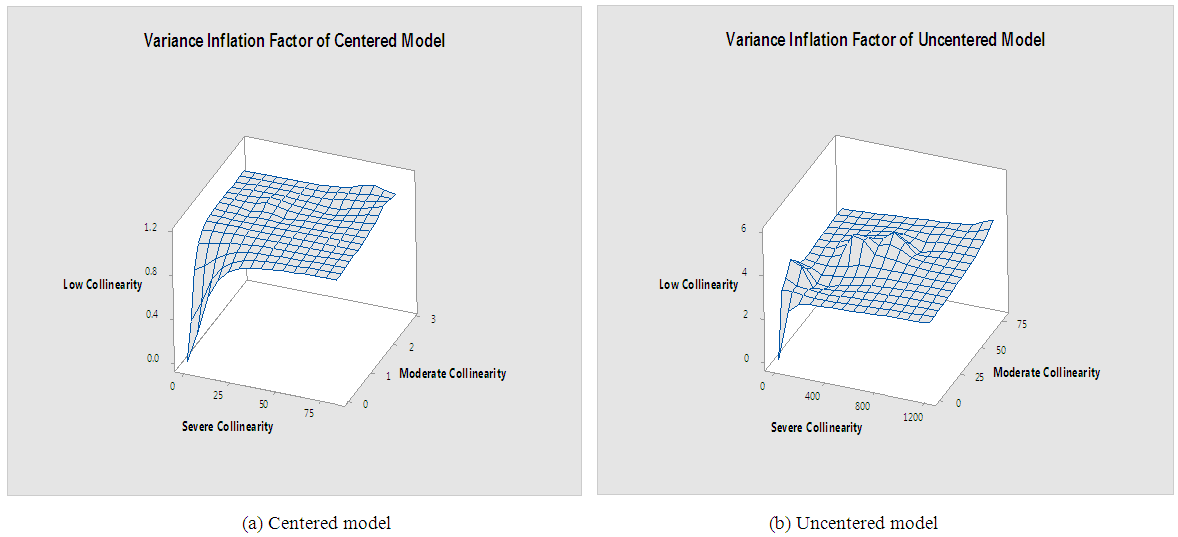
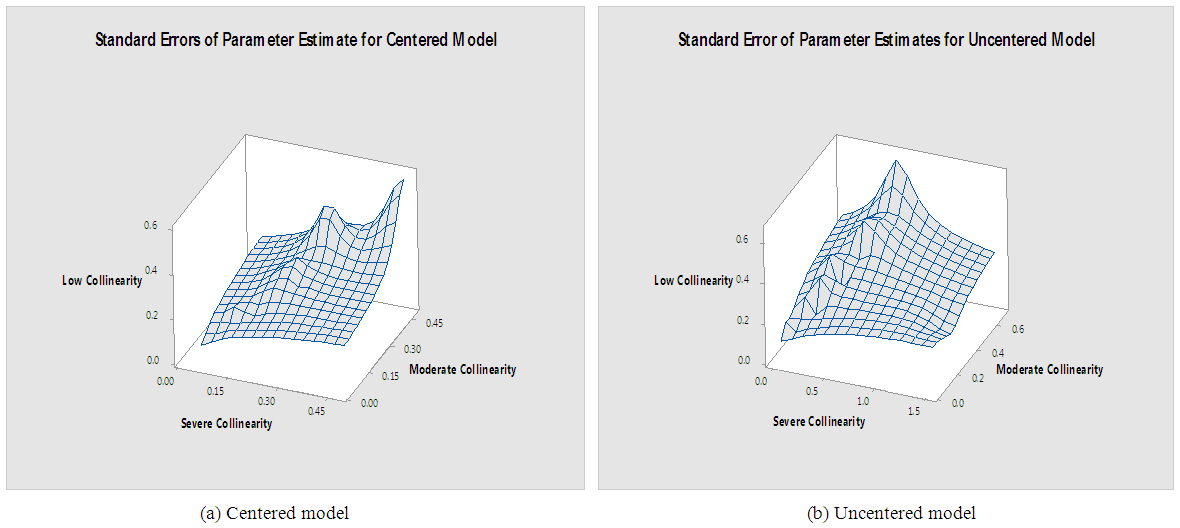
It has been recognized that centering can reduce collinearity among explanatory variables in a linear regression models. However, efficiency of centering as a solution to multicollinearity highly depends on correlation structure among predictive variables. In this paper, simulation study was performed in a polynomial model to examine the effect of centering at various level of collinearity. The results empirically verify that centering first dramatically reduces the collinearity whereas under severe collinearity, centering provides only a small improvement over no centering at all. Therefore application of centering as a solution to multicollinearity problem should be discouraged under severe collinearity.
Keywords: Centering, Regression model, Polynomial Regression, Ill conditioned model
Cite this paper: Ijomah Maxwell Azubuike, Second Order Regression with Two Predictor Variables Centered on Mean in an Ill Conditioned Model, International Journal of Statistics and Applications, Vol. 9 No. 4, 2019, pp. 101-110. doi: 10.5923/j.statistics.20190904.01.
1. Introduction
- Regression analysis is a statistical method widely used in many fields such as Statistics, economics, technology, social sciences and finance. A linear regression model is constructed to describe the relationship between the dependent variable and one or several independent variables. All procedures used and conclusions drawn in a regression analysis depend on assumptions of a regression model. The most used model is the classic linear regression model and the most used method for estimating classic model parameters is the Ordinary Least Squares (OLS).The linear regression model
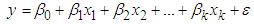 | (1) |
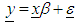 | (2) |
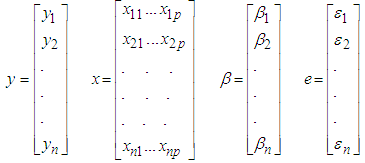 Normal equation in matrix form. Given n
Normal equation in matrix form. Given n  for one predictor variable (say
for one predictor variable (say  )
)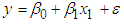 | (3) |
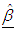 can be written as
can be written as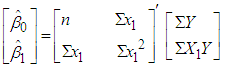 | (4) |
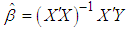 Under the classic assumptions, the OLS method has some attractive statistical properties that have made it one of the most powerful and popular methods of regression analysis. However, OLS is not appropriate if the explanatory variables exhibit strong pair wise and/or simultaneous correlation (multicollinearity), causing the design matrix to become non-orthogonal or worse, ill-conditioned. Once the design matrix is ill-conditioned, the least squares estimates are seriously affected, e.g., instability of parameter estimates, reversal of expected signs of the coefficients, masking of the true behavior the linear model being explored, etc. Furthermore, it reveals that small change in the data may lead to large differences in regression coefficients, and causes a loss in power and makes interpretation more difficult since there is a lot of common variation in the variables (Vasu and Elmore 1975; Belsley 1976; Stewart 1987; Dohoo et al., 1996; Tu et al., 2005).The problem of multicollinearity commonly exists among economic indicators that are influenced by similar policies that lead their simultaneous movement along similar directions.Whether co-integration exists or not among the predictors, simultaneous drifting away in some directions especially among time series that exhibit non-stationary behavior is common.There are many solutions proposed in the literature to address this problem. Among them are Dropping of variables (Carnes and Slade, 1988), the general shrinkage estimators (Hoerl and Kennard 1980; McDonald and Galarncau, 1975; George and Oman, 1996; McDonald, 1980), principal component regression (Butler and Denham, 2000), then centering (Aiken & West 1991, Cronbach 1987, Irwin & McClelland 2001). However, there is a growing debate on whether or not to involve centering as a solution for a collinear regression. It has been argued that the source of any discrepancies among statistical findings based on regression analyses in absence of centering is not mysterious; they can always be explained and resolved. Various researchers including Aiken and West (1991); Cronbach (1987), and Jaccard, Wan & Turrisi (1990); Irwin & McClelland, (2001); and Smith & Sasaki, (1979) recommend mean centering the variables x1 and x2 as an approach to alleviating collinearity related concerns. Aiken, West and others further recommend that one centre only in the presence of interactions. Centering aids interpretation and reduces the potential for multicollinearity (Aiken and West 1991). It is therefore a strategy to prevent errors in statistical inference. Aiken and West (1991) also imply that mean-centering reduces the covariance between the linear and interaction terms, thereby increasing the determinant of X’X. This viewpoint that collinearity can be eliminated by centering the variables, thereby reducing the correlations between the simple effects and their multiplicative interaction terms is echoed by Irwin and McClelland (2001, p. 109). Centering is recommended in order to eliminate collinearities which are due to the origins of the predictor variables and it can often provide computational benefits when small storage or low precision prevail (Marquardt and Snee, 1975). However, in contrast to Cronbach’s injunction, other authors (Glantz & Slinker, 2001; Kromrey & Foster-Johnson, 1998; Belsley, 1984; Echambadi & Hess 2007) take the stand that centering doesn’t usually change the statistical results, is necessary only in certain circumstances, and can thus easily be. Few authors like Hocking (1984), Snee (1983), Belsley (1984b), have attempted to address this problem but did not extend to the polynomial regression especially the two predictor variables. The problem of centering is therefore an issue which is still not completely resolved. In this article, we clarify the issues and reconcile the discrepancy. Therefore the aim of this paper is to compare the statistical estimates of a centered mode in a second order regression model at various degrees of collinearity for two predictor variables (X1&X2) in a linear component, quadratic component and interaction (cross product). The rest of the paper is mapped out as follows: Section 2 presents related literature and theoretical perspective of polynomial regression. Section 3 is the materials and methods of the paper, following interpretation of the empirical result, section 4 is the conclusion of the paper.
Under the classic assumptions, the OLS method has some attractive statistical properties that have made it one of the most powerful and popular methods of regression analysis. However, OLS is not appropriate if the explanatory variables exhibit strong pair wise and/or simultaneous correlation (multicollinearity), causing the design matrix to become non-orthogonal or worse, ill-conditioned. Once the design matrix is ill-conditioned, the least squares estimates are seriously affected, e.g., instability of parameter estimates, reversal of expected signs of the coefficients, masking of the true behavior the linear model being explored, etc. Furthermore, it reveals that small change in the data may lead to large differences in regression coefficients, and causes a loss in power and makes interpretation more difficult since there is a lot of common variation in the variables (Vasu and Elmore 1975; Belsley 1976; Stewart 1987; Dohoo et al., 1996; Tu et al., 2005).The problem of multicollinearity commonly exists among economic indicators that are influenced by similar policies that lead their simultaneous movement along similar directions.Whether co-integration exists or not among the predictors, simultaneous drifting away in some directions especially among time series that exhibit non-stationary behavior is common.There are many solutions proposed in the literature to address this problem. Among them are Dropping of variables (Carnes and Slade, 1988), the general shrinkage estimators (Hoerl and Kennard 1980; McDonald and Galarncau, 1975; George and Oman, 1996; McDonald, 1980), principal component regression (Butler and Denham, 2000), then centering (Aiken & West 1991, Cronbach 1987, Irwin & McClelland 2001). However, there is a growing debate on whether or not to involve centering as a solution for a collinear regression. It has been argued that the source of any discrepancies among statistical findings based on regression analyses in absence of centering is not mysterious; they can always be explained and resolved. Various researchers including Aiken and West (1991); Cronbach (1987), and Jaccard, Wan & Turrisi (1990); Irwin & McClelland, (2001); and Smith & Sasaki, (1979) recommend mean centering the variables x1 and x2 as an approach to alleviating collinearity related concerns. Aiken, West and others further recommend that one centre only in the presence of interactions. Centering aids interpretation and reduces the potential for multicollinearity (Aiken and West 1991). It is therefore a strategy to prevent errors in statistical inference. Aiken and West (1991) also imply that mean-centering reduces the covariance between the linear and interaction terms, thereby increasing the determinant of X’X. This viewpoint that collinearity can be eliminated by centering the variables, thereby reducing the correlations between the simple effects and their multiplicative interaction terms is echoed by Irwin and McClelland (2001, p. 109). Centering is recommended in order to eliminate collinearities which are due to the origins of the predictor variables and it can often provide computational benefits when small storage or low precision prevail (Marquardt and Snee, 1975). However, in contrast to Cronbach’s injunction, other authors (Glantz & Slinker, 2001; Kromrey & Foster-Johnson, 1998; Belsley, 1984; Echambadi & Hess 2007) take the stand that centering doesn’t usually change the statistical results, is necessary only in certain circumstances, and can thus easily be. Few authors like Hocking (1984), Snee (1983), Belsley (1984b), have attempted to address this problem but did not extend to the polynomial regression especially the two predictor variables. The problem of centering is therefore an issue which is still not completely resolved. In this article, we clarify the issues and reconcile the discrepancy. Therefore the aim of this paper is to compare the statistical estimates of a centered mode in a second order regression model at various degrees of collinearity for two predictor variables (X1&X2) in a linear component, quadratic component and interaction (cross product). The rest of the paper is mapped out as follows: Section 2 presents related literature and theoretical perspective of polynomial regression. Section 3 is the materials and methods of the paper, following interpretation of the empirical result, section 4 is the conclusion of the paper. 2. Polynomial Regression
- In Statistics polynomial regression is a form of linear regression in which the relationship between the independent variable x and the dependent variable y is modeled as an nth degree polynomial. Polynomial regression fits a nonlinear relationship between the value of x and the corresponding conditional mean of y, denoted E(y/x). In general, we can model the expected value of y as an nth degree polynomial. The polynomial regression model may contain one, two, or more than two predictor variables. Each predictor variable may be present in various powers.
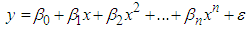 | (5) |
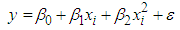 | (6) |
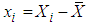 This polynomial model is called a second-order with one predictor variable because the single predictor variable is expressed in the model to the first and second powers. The predictor variable is centered – that is, expressed as a deviation around its mean and that the ith centered observation is denoted by.The two predictor variables of second order is given by
This polynomial model is called a second-order with one predictor variable because the single predictor variable is expressed in the model to the first and second powers. The predictor variable is centered – that is, expressed as a deviation around its mean and that the ith centered observation is denoted by.The two predictor variables of second order is given by 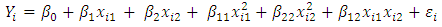 | (7) |
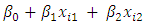 represents the linear component,
represents the linear component, 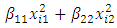 = quadratic component and
= quadratic component and 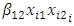 which is the cross product or interaction component. The above is a second-order model with two predictor variables. The response function is:
which is the cross product or interaction component. The above is a second-order model with two predictor variables. The response function is: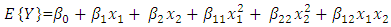 | (8) |
3. Materials and Methods
- To show the effect of mean centering on an ill-conditioned regression model, we ran a Monte Carlo simulation study using SAS 9.0 version. We begin by multiplying each of the selected variable with 0.5 in order to make the variables uniform. U= ranuni (start)X1=U+rannor (start)*0.5X2=U+rannor (start)*0.5Y=1+X1+X2+rannor (start)That is, we set ρX1, Y=ρX2, Y= 0.5 to represent modest sized effects of two predictors on the dependent variable, and varied the extent of multicollinearity, ρX1, X2 from 0.1 to 0.9. To achieve the objective of varying collinearity, we perturb the random error μ by multiplying it with values (i.e. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 30). This generates different values of the correlation coefficient between the two explanatory variables as shown in table 1.
|
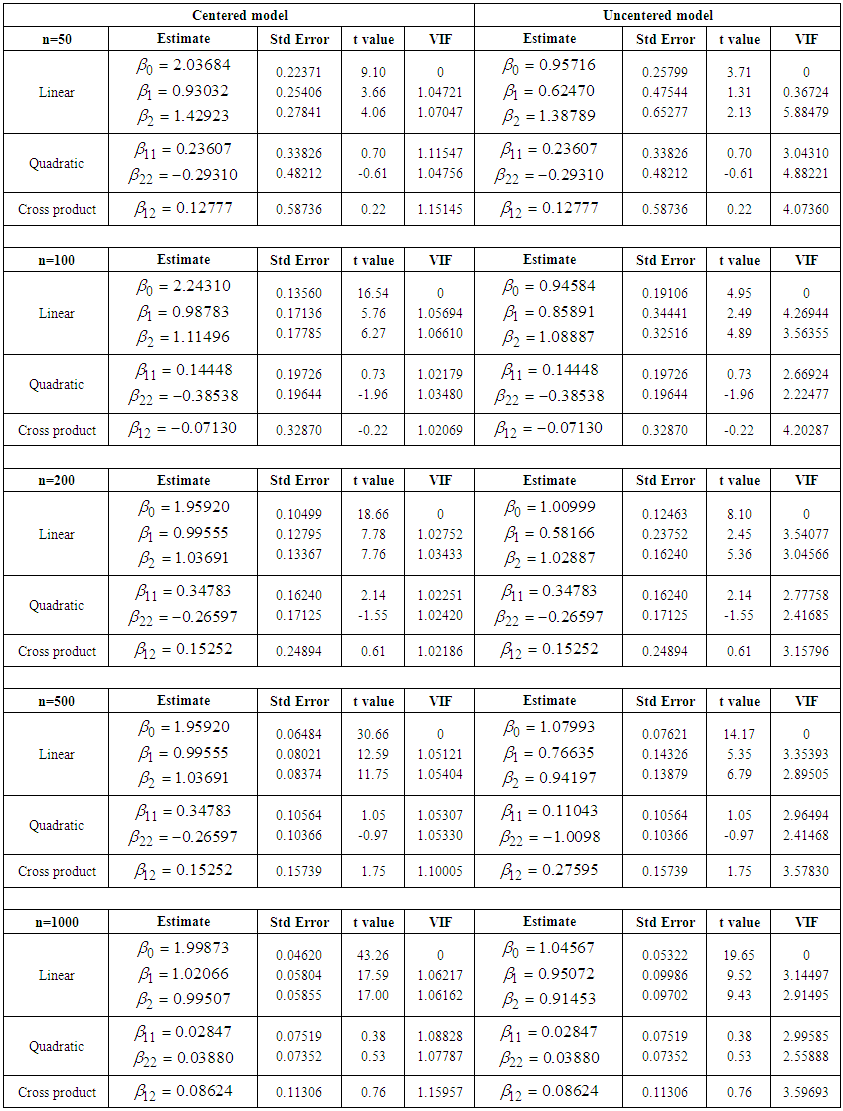 | Table 2. Centered and Uncentered models with low collinearity |
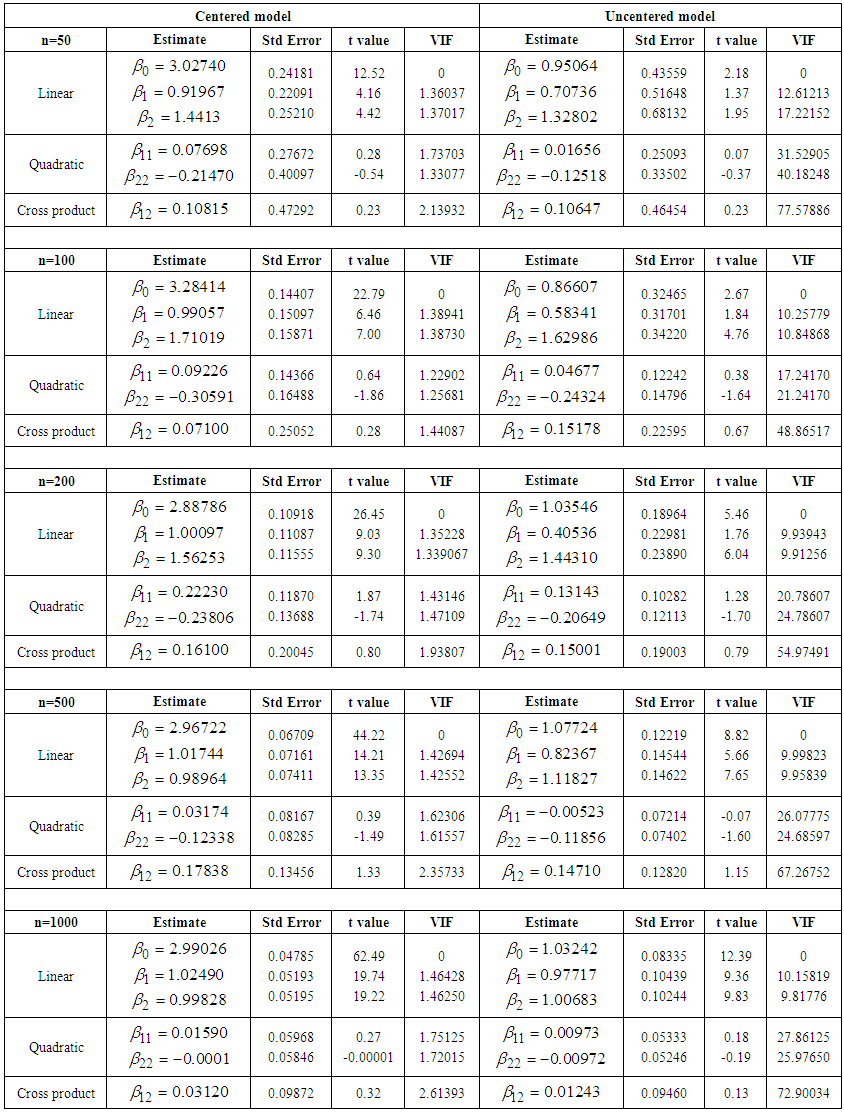 | Table 3. Centered and Uncentered models with moderate collinearity |
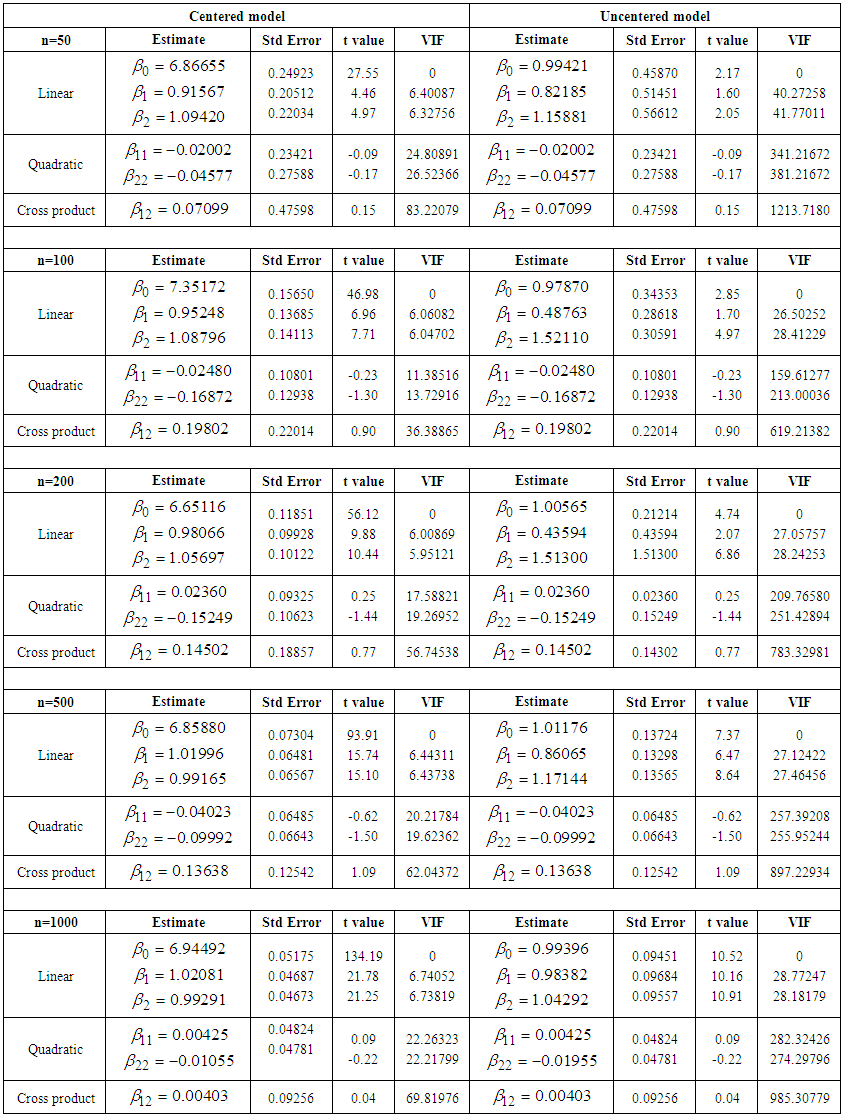 | Table 4. Centered and Uncentered models with severe collinearity |
4. Conclusions
- In this analysis, we focused on how three components (linear, quadratic and interaction) behave in centered and uncentered models to an ill conditioned regression using different collinearity structure (low, moderate and severe). A simulation study considering regression model with linear, quadratic and interaction components for centered and uncentered models was established. The result showed that the linear effect is significant in both the uncentered and mean-centered models for all the three considered collinearity structures, whereas quadratic and interaction effect were insignificant. Also, when there is a meaningful interaction among the variables, the linear effect will not equal the quadratic and interaction effect. It is worth to note that even the improvement offered by mean centering has its limits. When correlations is very strong, results begin to be affected even if the variables have been mean centered. The author believes that centering alleviates muticollinearity problem but it necessary to consider the degree of collinearity among the explanatory variables before using mean centering. For severe collinearity, use of centering should be discouraged especially for quadratic and interaction components.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML