-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2019; 9(3): 74-78
doi:10.5923/j.statistics.20190903.02

A Method for Constructing Super Saturated Design and Nearly Orthogonal Design with Mixed Level Orthogonal Design
Sunita Khurana, Shakti Banerjee
School of Statistics, Devi Ahilya University, Indore, M.P., India
Correspondence to: Shakti Banerjee, School of Statistics, Devi Ahilya University, Indore, M.P., India.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Orthogonal arrays such as factorial and fractional factorial designs of experimental plans are used for identifying important factors to improve quality of an experiment. Super Saturated designs are very cost-effective in the stage of scientific investigations. Nearly-Orthogonal arrays that can construct a variety of small-run designs with different levels have good statistical properties. In the present paper Super Saturated design and Nearly Orthogonal design are constructed with Orthogonal design. It is a great deal of interest in the development of factor screening experiments that are optimal or highly efficient under the E (s2) and J2 criterion.
Keywords: Orthogonal design, Nearly Orthogonal design, Super saturated design, Hadamard matrix, D-optimality, J2-optimality
Cite this paper: Sunita Khurana, Shakti Banerjee, A Method for Constructing Super Saturated Design and Nearly Orthogonal Design with Mixed Level Orthogonal Design, International Journal of Statistics and Applications, Vol. 9 No. 3, 2019, pp. 74-78. doi: 10.5923/j.statistics.20190903.02.
Article Outline
1. Introduction
- The field, statistical design of experiments (DoE) was born in the 1920’s by the pioneering work of Fisher (2000) in the agriculture arena. A design for a two-level factor screening experiment constructed saturated design (SD) from orthogonal design if the number of factors, ‘p’ is equal to ‘n – 1’, where n is the number of runs. Some examples of saturated design are Plackett–Burman designs (Plackett and Burman 1946) [1] and p- efficient designs (Lin 1993) [2]. When p > n − 1, the design is called a supersaturated design (SSD). Supersaturated designs were introduced by Booth and Cox (1962) [3] and were not studied further until the important work of Lin (1993a) [4] and Wu (1993) [5]. Since then, much work has been done on this subject, recently by Bulutoglu and Cheng (2004) [6], Jones, Lin, and Nachtsheim (2008) [7], Bulutoglu (2007) [8] and Ryan and Bulutoglu (2007) [9]. A commonly used criterion defined by Booth and Cox (1962) [3] for choosing an SSD is the E(s2) criterion, including minimization of E(s2) or ave(s2) and minimization of maximum column correlation for evaluating and comparing designs. Nguyen (1996) [10] constructing two level supersaturated design from incomplete block design.The concept of Orthogonal Array (OA) dates back to(Rao 1947) [11]. OAs has been used widely in manufacturing and high-technology industries for quality and productivity improvement experiments, as accounted by many industrial case studies and recent design textbooks (Montgomery 1997) [12]; (Wu and Hamada 2000) [13]. Applications of Nearly Orthogonal designs (NOAs) have been described by Wang and Wu (1992) [14]. From an estimation point of view, all of the main effects of an OA are estimable and orthogonal to each other, whereas all the main effects of an NOA are still estimable, but some are partially aliased with other (Honguan xu 2002) [15]. Since balance is an important and required property in practice, the balance considered in this article is OA (12, 31, 29). The purpose of this article is to present a simple and effective construction of OAs and NOAs with mixed levels and small runs.In this paper, we focus on finding combinatorial solution of the experiment. The experimental design considers an n× p matrix of factor settings, with a row corresponding to each of n design points and a column corresponding to each of p factors. This work has several steps, we clarify them as:• We proposed a class of special super saturated design of the experiment which can be easily constructed via half fraction of the Hadamard matrices.• We define mixed designs as designs with different factor types and different factor levels (e.g., factor 1 with 3 levels, factor 9 with 2 levels). Throughout this paper, we use the terms “qualitative” and “categorical” interchangeably, and may refer to discrete and continuous factors as “quantitative” or “numerical.”• We checked the pairwise correlation (ρ) between any two factors (columns). An orthogonal design has ρ = 0. If a design has 0 < ρ ≤ 0.05, it is called a nearly orthogonal design. • Finally, we analyze a design as efficient with optimality E (s2) and J2 criterion if the number of design points is acceptable.The purpose of this paper is to propose a framework for generating a design which is supersaturated design, nearly orthogonal and also balanced design with a minimum number of design points n. Section 2 articulates the Super Saturated design using Hadamard design in Thalassemic children. Section 3 shows that a solution for the problem which is an E (s2) - optimal SSD. Section 4 describes about an algorithm for constructing mixed-level OAs and nearly orthogonal designs (NOAs). Section 5 introduces the concept of J2 -optimality and other optimality criteria. Section 6 contains concluding remarks.
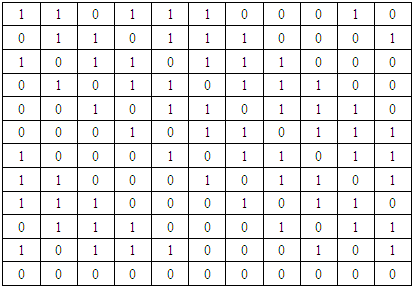
2. Supersaturated Design Using Hadamard Design for Thalassemic Children
- To have efficient analytical results a methodology for the design of an experiment was proposed in order to find as many as possible schemes containing maximum number of factors having different levels for the smallest number of experimental runs. This design study is based on an experiment which was conducted in order to obtain sufficient factors for accurate results. For the experiment, this study selected 250 Thalassemic children aged 8-18 years to analyze the impact of thalassemia disease and treatment pattern of thalassemic children.Consider two-level factorial experiments with p factors and ‘n’ observations, n being even. Denote the two levels of a factor by + 1 and -1. Then the design is determined by, n X p matrix of elements and the ith column ri gives the sequence of factor levels for factor ‘i’ in ‘n’ observations (1, 2, ..., n). We only consider the designs of the columns consisting of
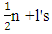 and
and 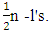 Now in an ordinary factorial experiment, where we assume interactions being ignored, the efficient and simple estimation of main effects by calculating the orthogonality of all design columns (Plackett & Burman, 1946) [1] is ensured. So, the condition required is,
Now in an ordinary factorial experiment, where we assume interactions being ignored, the efficient and simple estimation of main effects by calculating the orthogonality of all design columns (Plackett & Burman, 1946) [1] is ensured. So, the condition required is,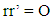 | (1) |
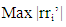 | (2) |
|
|
3. E (s2) as a Measure of Goodness of Supersaturated Designs
- We present a method for constructing two-level supersaturated designs (SSDs) from orthogonal designs. A lower bound of E(s2) that also covers the case of odd run sizes is given. This bound is attained by SSDs constructed from orthogonal designs. Let X be an n*p design matrix of a design with n runs and m two level factors each with 1/2n of +1 or high level value and 1/2n of -1 or low level values (p>n-1). Let Sij be the element in the ith row and jth column of X’X. Booth and Cox (1962) proposed on a criterion for comparing design the minimization of ave(S2). Where ave(s2) =
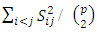 Clearly the orthogonal design ave(S2)=0.The rationale of the Booth-Cox criterion can be explained by using the singular value decomposition to decompose X as UA1/2V’ where matrices U and V are orthogonal and A is diagonal. It can be shown that X’X and XX’ share the same set of non-zero eigenvalues (λ1, ..., λr). Where, r =rank(X’X)=rank(XX’). Moreover
Clearly the orthogonal design ave(S2)=0.The rationale of the Booth-Cox criterion can be explained by using the singular value decomposition to decompose X as UA1/2V’ where matrices U and V are orthogonal and A is diagonal. It can be shown that X’X and XX’ share the same set of non-zero eigenvalues (λ1, ..., λr). Where, r =rank(X’X)=rank(XX’). Moreover 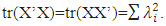 Thus, minimizing
Thus, minimizing 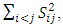 which is equivalent to minimizing tr (X’X)2), is the same as making the λi ‘s equal as possible with
which is equivalent to minimizing tr (X’X)2), is the same as making the λi ‘s equal as possible with 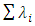 = constant.This in a sense is an approximation of the A-Optimality criterion, which requires the maximization of
= constant.This in a sense is an approximation of the A-Optimality criterion, which requires the maximization of 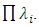 Because the sum of each column of X is 0, the sum of the elements of XX’ is 0 i.e. the sum of the off diagonal elements of XX’ equal to –np (np is the sum of the diagonal elements of XX’).Thus, the sum of square of elements of XX’ and X’X will reach the minimum if XX’ is of the form (p-x) In+Jn where x=-p/n-1 (assuming p is divisible by n-1), In is the identity matrix and Jn is the n*n matrix of 1’s.In this case ave (S2) = n (p2+ (n-1) x2-pn)/p (p-1) = n2(p-n+1)/(n-1)(p-1).
Because the sum of each column of X is 0, the sum of the elements of XX’ is 0 i.e. the sum of the off diagonal elements of XX’ equal to –np (np is the sum of the diagonal elements of XX’).Thus, the sum of square of elements of XX’ and X’X will reach the minimum if XX’ is of the form (p-x) In+Jn where x=-p/n-1 (assuming p is divisible by n-1), In is the identity matrix and Jn is the n*n matrix of 1’s.In this case ave (S2) = n (p2+ (n-1) x2-pn)/p (p-1) = n2(p-n+1)/(n-1)(p-1).4. Construction of Nearly Orthogonal Design for Thalassemic Children
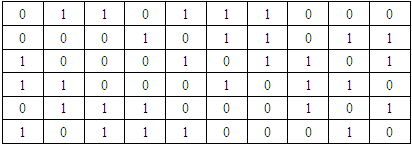
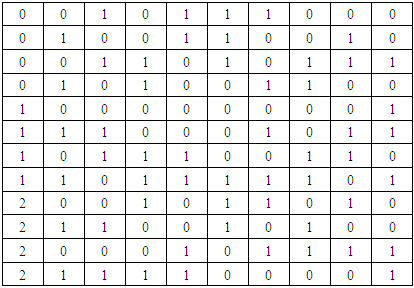
- We assume that the research and development department of the health care wants to know whether there is a more economical design. Nearly Orthogonal design consider another study conducted to examine 12 factors affecting the children suffering with Thalassemia: Age of chelation therapy was started (less than 5 years, 1-5 years, above 5 years) Pale appearance(yes/no), Less appetite(yes/no), Frequent history of temperature(yes/no), No weight & height gain(yes/no), Pneumonia(yes/no), Loose motion & vomiting(yes/no), Irritation(yes/no), Less hemoglobin(yes/no), Very weak/dull/ less active(yes/no), frequently sick(yes/no), cough & cold(yes/no), Jaundice(yes/no), Previous history in family(yes/ no). To ensure that all the main effects are estimated clearly from one another, it is desirable to use an orthogonal array (OA). The smallest OA is found for one three-level factor and nine two-level factors. However, we want to reduce the cost of this experiment and plan to use a 12-run design. A good solution then is to use a 12-run nearly-orthogonal array (NOA).Consider the matrix of Table: 2 below, of OA (12, 31, 29) the first column has three levels and the other 9 columns have two levels each. For illustration wk=1 is chosen for all k. Now we consider a design comprising the first five columns of OA (12, 31, 29).
|
5. J2 Optimality Criterion
- The concept of J2-optimality criteria for
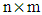 matrix d=[xik], weight wk>0 is assigned for column k, which has sk levels. For 1≤ i< j≤ N, let
matrix d=[xik], weight wk>0 is assigned for column k, which has sk levels. For 1≤ i< j≤ N, let 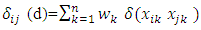 , where
, where 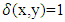 if x=y and 0 otherwise. The
if x=y and 0 otherwise. The 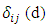 value measures the similarity between the ith and jth rows of d. In particular, if wk=1 is chosen for all k, then
value measures the similarity between the ith and jth rows of d. In particular, if wk=1 is chosen for all k, then 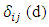 is the number of coincidences between the ith and jth rows.Define
is the number of coincidences between the ith and jth rows.Define 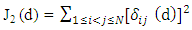 A design is optimal if it minimizes J2. By minimizing J2(d), it is desired that the rows of d be as dissimilar as possible. The following lemma shows an important lower bound of J2.Lemma: For an
A design is optimal if it minimizes J2. By minimizing J2(d), it is desired that the rows of d be as dissimilar as possible. The following lemma shows an important lower bound of J2.Lemma: For an 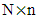 matrix d whose kth column has sk levels and weight wk,
matrix d whose kth column has sk levels and weight wk,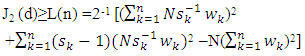 | (3) |
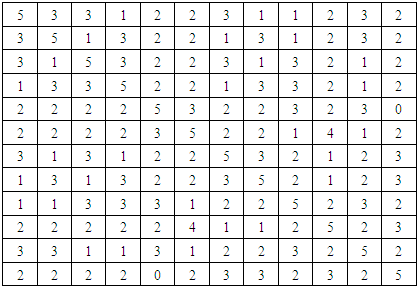 It is easy to verify that J2=330 and that the lower bound in (3) is also 330 for one factor have 3 level and four factor have 2 level column with wk=1. Therefore, we consider the first five columns from OA (12, 31, 29), because the J2 value equals the lower bound.Next, consider the whole array, comprising all 10 columns. Same calculation shows that J2= 1284 and that the lower bound of (3) is 1260. Therefore, the whole array is not an OA because the J2 value is greater than the lower bound.
It is easy to verify that J2=330 and that the lower bound in (3) is also 330 for one factor have 3 level and four factor have 2 level column with wk=1. Therefore, we consider the first five columns from OA (12, 31, 29), because the J2 value equals the lower bound.Next, consider the whole array, comprising all 10 columns. Same calculation shows that J2= 1284 and that the lower bound of (3) is 1260. Therefore, the whole array is not an OA because the J2 value is greater than the lower bound.6. Conclusions
- The result of this paper enlightens us with an efficient construction method for Super Saturated and Nearly Orthogonal designs. An efficient design was needed to investigate or generate those variables and combinations which are important. In our study an orthogonal main effect plan would require clinical testing of 12 thalassemia children, but with super saturated design we can test only 6 children. The resultant arrays are optimal with respect to E(s2) and J2 optimality criteria. Advantage of these constructions are:- eased usability, flexibility for constructing various mixed level designs to generate several OA’s main effect plans. The proposed construction method is important because it can efficiently construct more new Nearly Orthogonal and Supersaturated designs with good projective properties.
ACKNOWLEDGMENTS
- We are grateful to an anonymous referee for their helpful and constructive comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML