A. Danbaba, A. Odeyale, Y. Musa
Department of Mathematics, Usmanu Danfodiyo University, Sokoto, Nigeria
Correspondence to: A. Danbaba, Department of Mathematics, Usmanu Danfodiyo University, Sokoto, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Researchers conduct the same experiments at different environments or periods (seasons) with similar treatments purposely to study the interaction between the treatments and environments or between the treatments and periods (seasons). The interest is to carry out joint analysis of these multi-environment experiments, instead of analyzing each experiment separately. However, Joint analysis of these experiments when conducted using orthogonal (Graeco) Sudoku square design is still missing in the literature. This paper proposed a method of obtaining joint analysis of many experiments carried out using orthogonal Sudoku square design of odd order in which experimental treatments are similar for each experiment. A numerical example was presented to explain the proposed method.
Keywords:
Joint analysis, Sudoku square design, Graeco Sudoku design, Multi-environment experiments
Cite this paper: A. Danbaba, A. Odeyale, Y. Musa, Joint Analysis of Several Experiments Conducted via Orthogonal Sudoku Design of Odd Order, International Journal of Statistics and Applications, Vol. 8 No. 6, 2018, pp. 323-331. doi: 10.5923/j.statistics.20180806.06.
1. Introduction
Many researchers conduct field experiments by randomized block design, Latin square design, balanced incomplete block design or Youden design over different environments such as locations or periods (seasons). Analysis of data from these experiments is usually carried out through joint analysis of all the experiments, instead of individual experiment. It was reported in [1] that one of the advantages of multi-environment analysis is that it increases the accuracy of evaluation (hence the accuracy of selection). There are two main reasons for multiple-environments trials as discussed in ([2], [3]). The reasons are neither mutually exclusive nor all inclusive. The first reason is to estimate the effects and comparative effects of treatments for specific environments or to estimate the effects of comparative effects of treatments over broad population of environments [2]. The second reason was to estimate the consistency of treatment effects for specific environments over broad populations of environments as in [3].In [6] the method of joint intra-block analysis of a group of experiments in complete randomized block, where some common treatments applied to all the experiments, series of examples were given, separate tables of analysis and table of the combined analysis were also given. They further gave the condition that must be met before combined analysis combined analysis can be carried out, as such, if the residual variance estimates from separate analyses are not too different a joint analysis can be carried out for the whole set of the experiments. Subsequently [11] following the same approach and obtained the joint analysis of balanced incomplete block designs with some common treatments applied to all the experiments of the multiple-environment, he also obtained the methods of adjusted treatment of sum of square and illustration was given. However, [5] discussed the combined analysis of Youden squares and Latin square designs with some common treatments as an extension of the work by [11]. [5] also said that the method can be used to analysis data from combined data set of Youden squares when some treatments are common while that of [6] can be used for combined analysis of a Latin square when some treatments are also common to all the experiments. The work of [9] discussed the appropriate analyses of combined experiments based on the constraint that the effects of random interactions with the Anova table and spilt-plot experiment combined over location or year. In [12], method of combined analysis when treatments are used to represents levels of quantitative factor but differ among experiments is presented. Multiple regression analysis was used when a continuous variable represents treatment levels, classification variables represents experiments and product of the continuous and classification variables represent differences among experiments. This assumption reflects a tradition in the analysis of fixed effects that, in most cases, is not appropriate for a random effect ([7], [10]). Recently, [4] presented a paper on combined analysis of Sudoku square designs with common treatments. The work in [4], also discussed combined analysis of data from multi- environment experiments using Sudoku square designs. Sudoku square design consists of treatments (Latin letters) which are arranged in a square array in such a way that each row, column and sub-square contains each of the treatments exactly once see [8]. In addition, [8] observed that Sudoku square design go beyond Latin square design with additional source of variation called box effect. An extension of the work of [8] is presented in [14], with additional terms in the models and in the source of variation namely; Row-block effect and column-block effect. For instance, [14] considered Sudoku of order 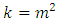 and gave detail analysis with illustrative examples and the application of Sudoku square to agricultural experiment. In addition, [13] extended the work of [14] to the construction of orthogonal Sudoku square design with additional source of variation i.e treatments (Greek and Latin) effects. In Line with [13], two Sudoku squares of the same order are said to be orthogonal Sudoku squares, if we superimpose the two Sudoku squares then one may get a pair of treatments ( Latin and Greek letters) in each row, column and sub-square only once. The work of [14] was used by [4] to carry out combined analysis of several experiments conducted in different environments using of Sudoku square design. However the Sudoku square design presented by [4] does not contains pair of treatments labeled with Greek and Latin letters occurring only once in each row, column and sub-square of the design. That is, the analysis in [4] is not on the orthogonal Sudoku square design.This paper proposed joint analysis of multi-environment experiments when implemented by mean of orthogonal Sudoku square design of odd order for which experimental treatments common in each environment or experiment. However, only orthogonal Sudoku square of order nine is considered for the study.
and gave detail analysis with illustrative examples and the application of Sudoku square to agricultural experiment. In addition, [13] extended the work of [14] to the construction of orthogonal Sudoku square design with additional source of variation i.e treatments (Greek and Latin) effects. In Line with [13], two Sudoku squares of the same order are said to be orthogonal Sudoku squares, if we superimpose the two Sudoku squares then one may get a pair of treatments ( Latin and Greek letters) in each row, column and sub-square only once. The work of [14] was used by [4] to carry out combined analysis of several experiments conducted in different environments using of Sudoku square design. However the Sudoku square design presented by [4] does not contains pair of treatments labeled with Greek and Latin letters occurring only once in each row, column and sub-square of the design. That is, the analysis in [4] is not on the orthogonal Sudoku square design.This paper proposed joint analysis of multi-environment experiments when implemented by mean of orthogonal Sudoku square design of odd order for which experimental treatments common in each environment or experiment. However, only orthogonal Sudoku square of order nine is considered for the study.
2. Method of Analysis
Assume that we have two environments of which experiments were conducted using orthogonal Sudoku square design (see Fig.1) each with k treatments with each treatment occurs only once in each (row, column or sub-block) such that 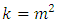 where
where 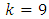 and
and 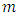 (number of row-block or column-block).In this study, four models of orthogonal Sudoku square designs discussed by [13] were modified and combined analysis from each were discussed under “g” environments. For all the models considered in this study, it is assumed that all effects are fixed.
(number of row-block or column-block).In this study, four models of orthogonal Sudoku square designs discussed by [13] were modified and combined analysis from each were discussed under “g” environments. For all the models considered in this study, it is assumed that all effects are fixed. 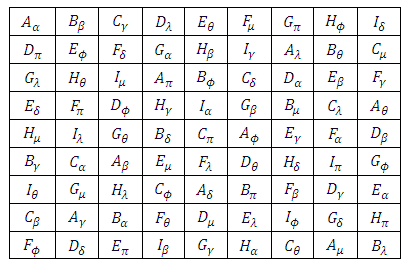 | Figure 1. Orthogonal Sudoku square of order 9 |
Model 1: The modification of Type I of [13] is as follows:The model assume row, column and treatment effects as in complete Latin square designs. In addition the row-block, column-block and square effects are in Sudoku square design: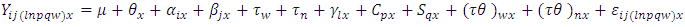 Where
Where  Where
Where 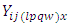 = Observation on experimental unit.
= Observation on experimental unit.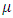 = Overall mean,
= Overall mean,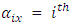 Row block effect in
Row block effect in 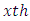 environment experiment,
environment experiment,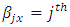 Column block effect in
Column block effect in 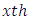 environment experiment,
environment experiment,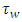 = Latin letter
= Latin letter 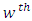 Treatment effect,
Treatment effect,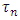 = Greek letter
= Greek letter 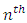 Treatment effect,
Treatment effect,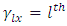 Row effect in
Row effect in 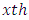 environment experiment,
environment experiment,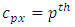 Column effect in
Column effect in 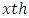 environment experiment,
environment experiment,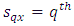 Sub-Square effect in
Sub-Square effect in 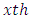 environment experiment,
environment experiment,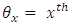 Environment-experiment,
Environment-experiment,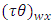 = Interaction between
= Interaction between 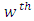 Latin Treatment and
Latin Treatment and 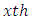 environment experiment,
environment experiment,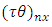 = Interaction between
= Interaction between 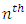 Greek Treatment and
Greek Treatment and 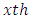 environment experiment,
environment experiment,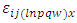 = Error component with mean zero and variance
= Error component with mean zero and variance 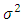
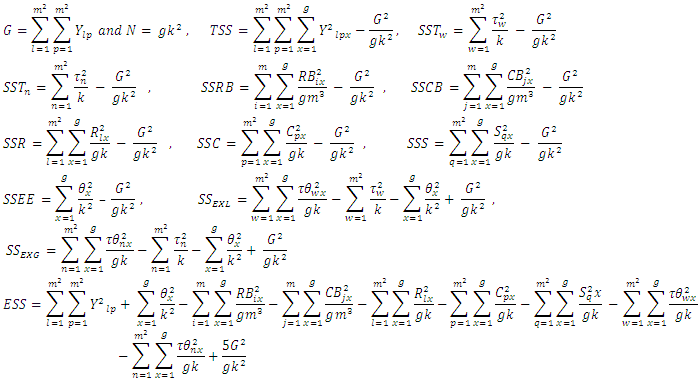
Table 1. ANOVA Table for Combined Graeco Sudoku square designs for model 1
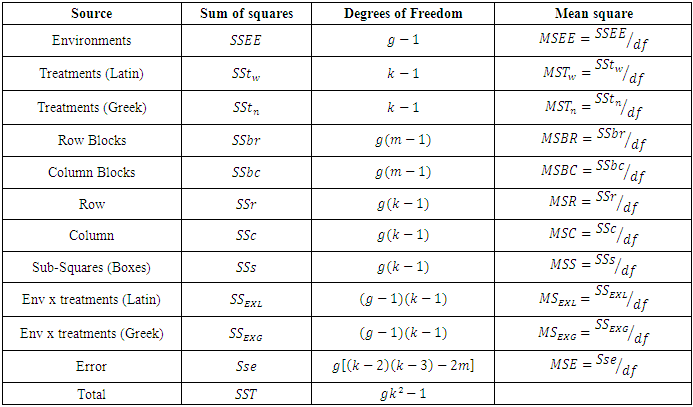 |
| |
|
Model 2: The modified linear model Type IIThe model assumed that row effects are nested in the row-block effects and the column effects are nested in the column-block effects.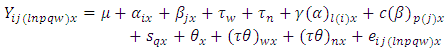 Where
Where 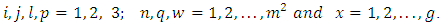 Where
Where 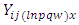 = Observation on experimental unit.
= Observation on experimental unit.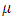 = Overall mean
= Overall mean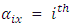 Row block effect in
Row block effect in 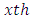 environment experiment,
environment experiment,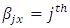 Column block effect in
Column block effect in 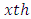 environment experiment,
environment experiment,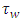 = Latin letter
= Latin letter 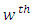 Treatment effect,
Treatment effect,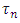 = Greek letter
= Greek letter 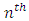 Treatment effect,
Treatment effect,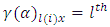 Row effect nested in
Row effect nested in 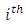 block (row) in
block (row) in 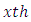 environment experiment,
environment experiment,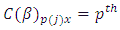 Column effect nested in
Column effect nested in 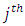 block (column) in
block (column) in 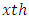 environment experiment,
environment experiment,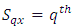 Sub-Square effect in
Sub-Square effect in 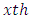 environment experiment,
environment experiment,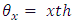 Environment-experiment,
Environment-experiment,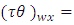 Interaction between
Interaction between 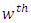 Latin Treatment and
Latin Treatment and 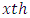 environment experiment,
environment experiment,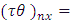 Interaction between
Interaction between 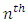 Greek Treatment and
Greek Treatment and 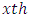 environment experiment,
environment experiment,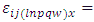 Error component with mean zero and variance
Error component with mean zero and variance 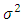
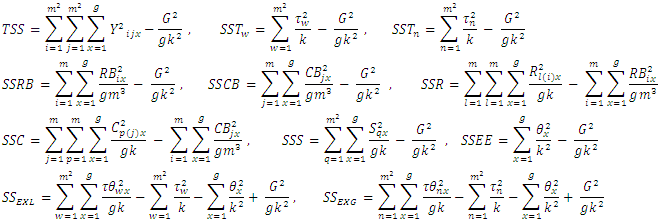
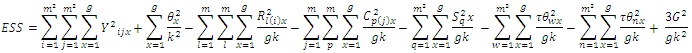
Table 2. ANOVA Table for Combined Graeco Sudoku square designs for model 2
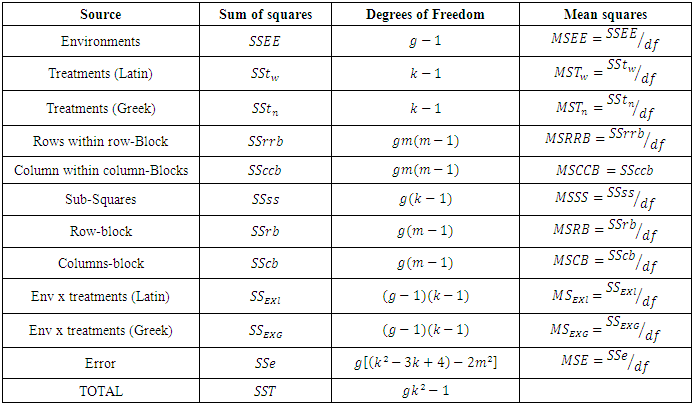 |
| |
|
Model 3: The modified linear model Type IIIIn this model it is assumed that the horizontal square effects are nested in the row block effects and the vertical square effects are nested in the column block effects.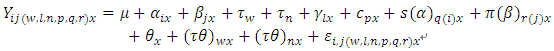 Where
Where 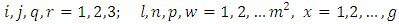 Where
Where 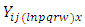 = Observation on experimental unit.
= Observation on experimental unit.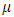 = Overall mean,
= Overall mean,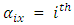 Row block effect in
Row block effect in 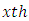 environment experiment,
environment experiment,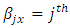 Column block effect in
Column block effect in 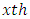 environment experiment,
environment experiment,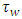 = Latin letter
= Latin letter 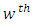 Treatment effect,
Treatment effect,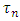 = Greek letter
= Greek letter 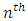 Treatment effect,
Treatment effect,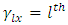 Row effect in
Row effect in 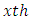 environment experiment,
environment experiment,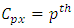 Row effect in
Row effect in 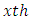 environment experiment,
environment experiment,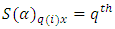 Row effect nested in
Row effect nested in 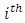 block (row) in
block (row) in 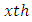 environment experiment,
environment experiment,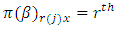 Column effect nested in
Column effect nested in 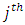 block (column) in
block (column) in 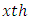 environment experiment,
environment experiment,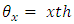 Environment-experiment,
Environment-experiment,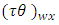 = Interaction between
= Interaction between 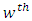 Latin Treatment and
Latin Treatment and 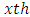 environment experiment,
environment experiment,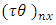 = Interaction between
= Interaction between 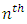 Greek Treatment and
Greek Treatment and 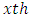 environment experiment,
environment experiment,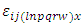 = Error component with mean zero and variance
= Error component with mean zero and variance 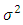
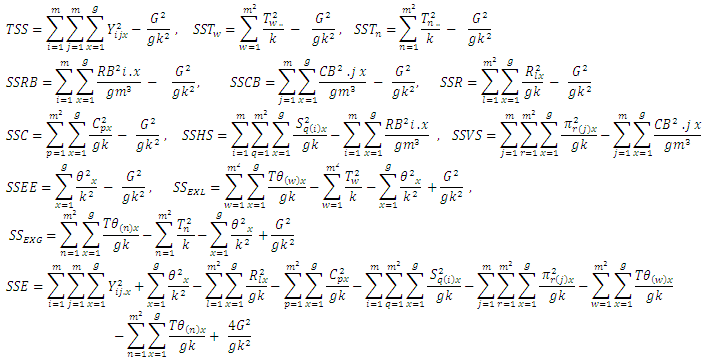
Table 3. ANOVA Table for Combined Graeco Sudoku square designs for model 3
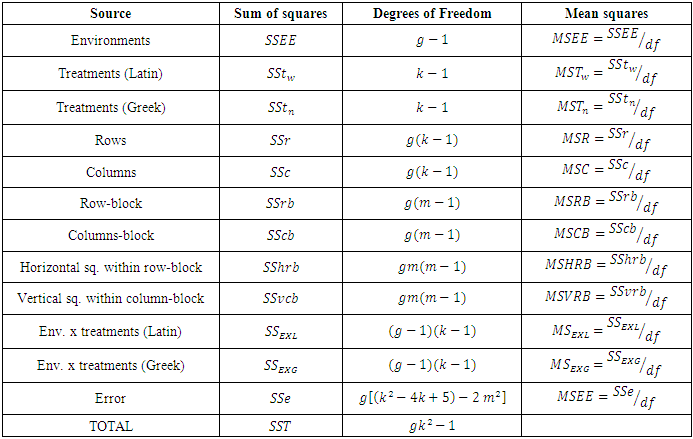 |
| |
|
Model 4: The modified linear model type IVIn this model it is assumed that the row effects and the horizontal square effects are nested in the row block effects and the column effects and the vertical square effects are nested in the column block effects.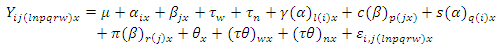 Where
Where 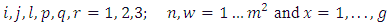 Where
Where 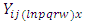 = Observation on experimental unit.
= Observation on experimental unit.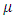 = General mean effect
= General mean effect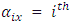 Row block effect in
Row block effect in 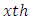 environment experiment,
environment experiment,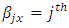 Column block effect in
Column block effect in 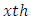 environment experiment,
environment experiment,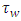 = Latin letter
= Latin letter 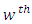 Treatment effect,
Treatment effect,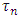 = Greek letter
= Greek letter 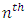 Treatment effect,
Treatment effect,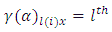 Row effect nested in
Row effect nested in 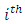 block (row) in
block (row) in 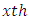 environment experiment,
environment experiment,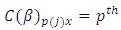 Column effect nested in
Column effect nested in 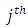 block (column) in
block (column) in 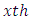 environment experiment,
environment experiment,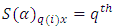 Horizontal Square effect nested in
Horizontal Square effect nested in 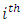 block (row) in
block (row) in 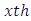 environment experiment,
environment experiment,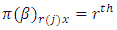 Vertical Square effect nested in
Vertical Square effect nested in 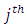 block (column) in
block (column) in 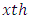 environment experiment,
environment experiment,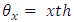 Environment-experiment,
Environment-experiment,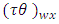 = Interaction between
= Interaction between 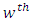 Latin Treatment and
Latin Treatment and 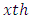 environment experiment,
environment experiment,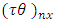 = Interaction between
= Interaction between 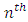 Greek Treatment and
Greek Treatment and 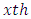 environment experiment,
environment experiment,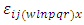 = Error component with mean zero and variance
= Error component with mean zero and variance 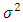
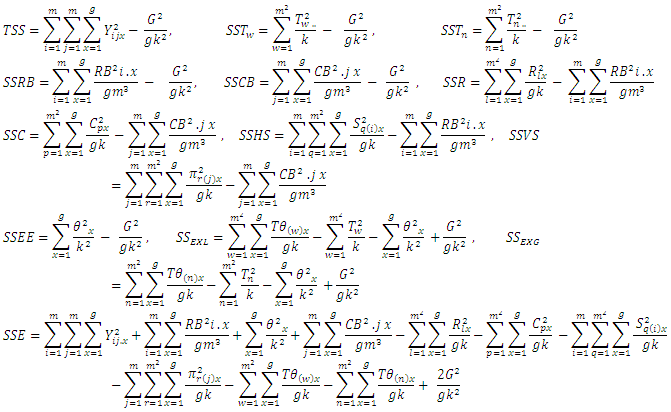
Table 4. ANOVA Table for Combined Graeco Sudoku square designs for model 4
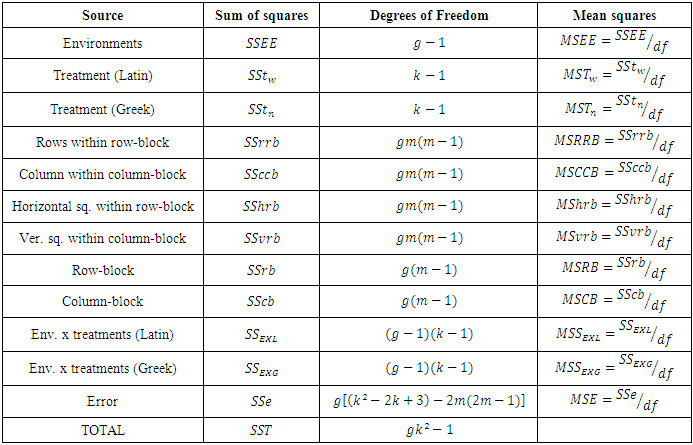 |
| |
|
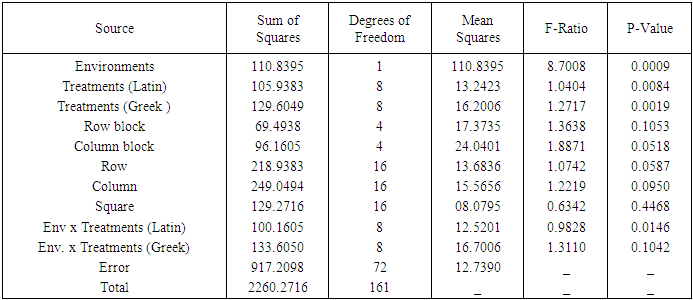
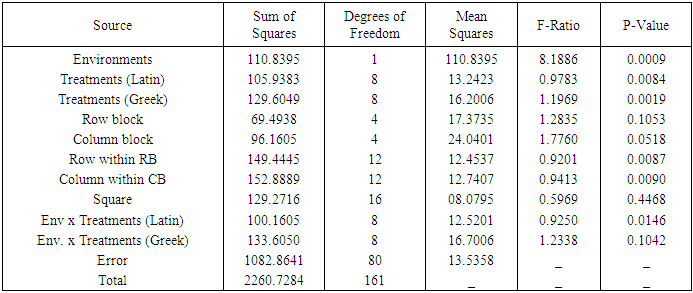
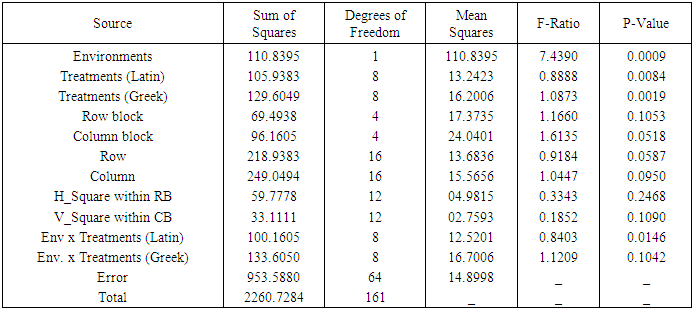
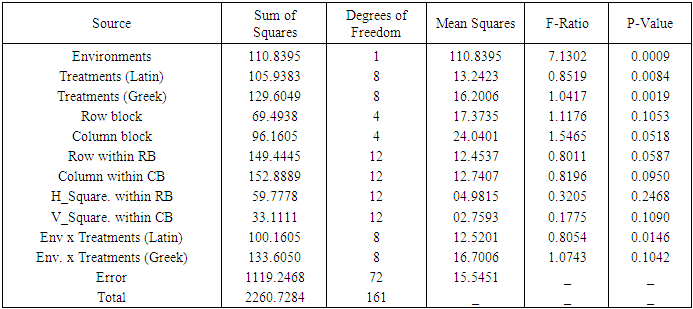
Illustration: Tables 5 and 6 give hypothetical datasets for two environments 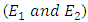 obtained using orthogonal Sudoku square designs of order 9. Data for E1 are presented in [13] for analysis of single orthogonal Sudoku design. Combined ANOVA tables obtained using R software for models 1 to 4 are presented in tables 7 to 10, respectively.
obtained using orthogonal Sudoku square designs of order 9. Data for E1 are presented in [13] for analysis of single orthogonal Sudoku design. Combined ANOVA tables obtained using R software for models 1 to 4 are presented in tables 7 to 10, respectively.Table 5. Hypothetical data of a Graeco Sudoku square design of order 9 (Environment I)
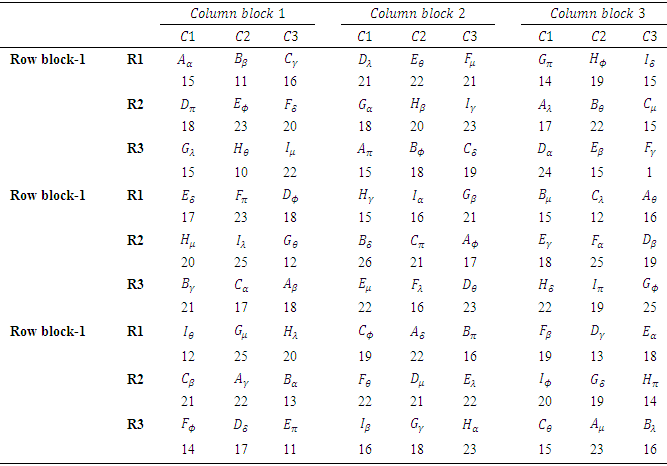 |
| |
|
Table 6. Hypothetical data of a Graeco Sudoku square design of order 9 (Environment II)
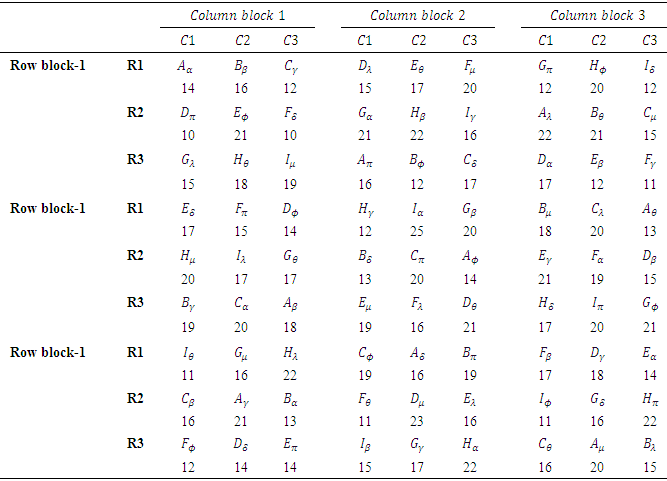 |
| |
|
Table 7. ANOVA Table for Combined analysis of Graeco Sudoku square design of type I of order 9
 |
| |
|
Table 8. ANOVA Table for Combined analysis of Graeco Sudoku square design of type II of order 9
 |
| |
|
Table 9. ANOVA Table for Combined analysis of Graeco Sudoku square design of type III of order 9
 |
| |
|
Table 10. ANOVA Table for Combined analysis of Graeco Sudoku square design of type IV of order 9
 |
| |
|
3. Conclusions
In this paper, joint analysis of orthogonal Sudoku design conducted for g environments is proposed. The method allows experimenter to tests/investigates the interaction effect between environments and treatment (Latin and Greek treatment). In addition, the models of the orthogonal Sudoku designs were modified to contain the interaction between treatments (Latin and Greek) and environments effects.
References
| [1] | Albassam, M.S. and Ali, M.A. (2014). Test statistics for combined treatment contrast under heterogeneous error variance and Latin square design. Pakistan J. Statist. Vol. 30(3), 345-360. |
| [2] | Bejar R., Fernandez C. Mateu C. Megda Valls M. (2012). The Sudoku Completion Problem With Rectangular Hole Pattern Is NP-Complete. Discrete Mathematics 312, 3306-3315. |
| [3] | Blouin D. C., Webster E. P., and Bond J. A. (2011). On the Analysis of Combined Experiments. Weed Technology 2011 25(1), 165–169. |
| [4] | Danbaba A. (2016). Combined Analysis of Sudoku Square Designs with Same Treatments. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering Vol: 10, No.4, 155-159. |
| [5] | Giri, N. C. (1963). Note: On the Combined Analysis of Youden Squares and of Latin Square Designs with Some Common Treatments. Biometrics, 19 (1), 171-174. |
| [6] | Gomes, F. F. and Guimares, R. F. (1958). Joint analysis of experiments incomplete randomized blocks with some common treatments. Biometrics 14, 521-526. |
| [7] | Hocking, R.R. (1985). The analysis of linear models. Brooks/Cole, Monterey, CA. |
| [8] | Hui-Dong M. and Ru-Gen, X. (2008). Sudoku Square- a New Design in field Experiment, Acta Agron Sin, 34(9), 1489–1493. |
| [9] | McIntosh, M. S. (1983). Analysis of combined experiments. Agron. Journal. 75:153–155. |
| [10] | Moore K. J. and Dixon P. M. (2015). Analysis of Combined Experiments Revisited, Agronomy Journal, 107(2), 763 – 771. |
| [11] | Pavate, M. V. (1961). Combined Analysis of Balanced Incomplete Block Designs with Some Common Treatments, Biometrics, 17(1), 111-119. |
| [12] | Paul N. H. and Mario, R. P. (1989). Combined analysis of experiments when treatments differ among experiments. Annual conference on applied Statistics in agriculture. Paper 20. |
| [13] | Subramani, J. (2012). Construction of Graeco Sudoku square Designs of Odd Orders, Bonfring International Journal of Data Mining, 2 (2), 37-41. |
| [14] | Subramani, J. and K.N. Ponnuswamy (2009). Construction and Analysis of Sudoku designs. Model Assisted Statistics and Applications, 4(4), 287-301. |



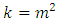 and gave detail analysis with illustrative examples and the application of Sudoku square to agricultural experiment. In addition, [13] extended the work of [14] to the construction of orthogonal Sudoku square design with additional source of variation i.e treatments (Greek and Latin) effects. In Line with [13], two Sudoku squares of the same order are said to be orthogonal Sudoku squares, if we superimpose the two Sudoku squares then one may get a pair of treatments ( Latin and Greek letters) in each row, column and sub-square only once. The work of [14] was used by [4] to carry out combined analysis of several experiments conducted in different environments using of Sudoku square design. However the Sudoku square design presented by [4] does not contains pair of treatments labeled with Greek and Latin letters occurring only once in each row, column and sub-square of the design. That is, the analysis in [4] is not on the orthogonal Sudoku square design.This paper proposed joint analysis of multi-environment experiments when implemented by mean of orthogonal Sudoku square design of odd order for which experimental treatments common in each environment or experiment. However, only orthogonal Sudoku square of order nine is considered for the study.
and gave detail analysis with illustrative examples and the application of Sudoku square to agricultural experiment. In addition, [13] extended the work of [14] to the construction of orthogonal Sudoku square design with additional source of variation i.e treatments (Greek and Latin) effects. In Line with [13], two Sudoku squares of the same order are said to be orthogonal Sudoku squares, if we superimpose the two Sudoku squares then one may get a pair of treatments ( Latin and Greek letters) in each row, column and sub-square only once. The work of [14] was used by [4] to carry out combined analysis of several experiments conducted in different environments using of Sudoku square design. However the Sudoku square design presented by [4] does not contains pair of treatments labeled with Greek and Latin letters occurring only once in each row, column and sub-square of the design. That is, the analysis in [4] is not on the orthogonal Sudoku square design.This paper proposed joint analysis of multi-environment experiments when implemented by mean of orthogonal Sudoku square design of odd order for which experimental treatments common in each environment or experiment. However, only orthogonal Sudoku square of order nine is considered for the study.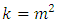 where
where 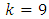 and
and 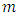 (number of row-block or column-block).In this study, four models of orthogonal Sudoku square designs discussed by [13] were modified and combined analysis from each were discussed under “g” environments. For all the models considered in this study, it is assumed that all effects are fixed.
(number of row-block or column-block).In this study, four models of orthogonal Sudoku square designs discussed by [13] were modified and combined analysis from each were discussed under “g” environments. For all the models considered in this study, it is assumed that all effects are fixed. 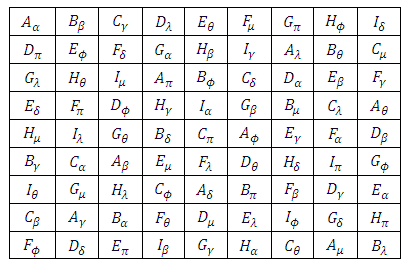
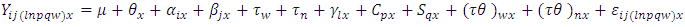 Where
Where  Where
Where  = Observation on experimental unit.
= Observation on experimental unit. = Overall mean,
= Overall mean,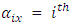 Row block effect in
Row block effect in 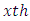 environment experiment,
environment experiment,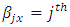 Column block effect in
Column block effect in 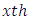 environment experiment,
environment experiment,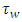 = Latin letter
= Latin letter 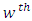 Treatment effect,
Treatment effect,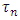 = Greek letter
= Greek letter 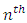 Treatment effect,
Treatment effect,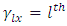 Row effect in
Row effect in 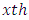 environment experiment,
environment experiment,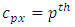 Column effect in
Column effect in 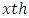 environment experiment,
environment experiment,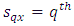 Sub-Square effect in
Sub-Square effect in 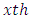 environment experiment,
environment experiment,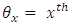 Environment-experiment,
Environment-experiment,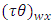 = Interaction between
= Interaction between 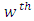 Latin Treatment and
Latin Treatment and 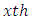 environment experiment,
environment experiment,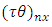 = Interaction between
= Interaction between 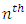 Greek Treatment and
Greek Treatment and 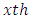 environment experiment,
environment experiment,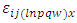 = Error component with mean zero and variance
= Error component with mean zero and variance 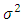
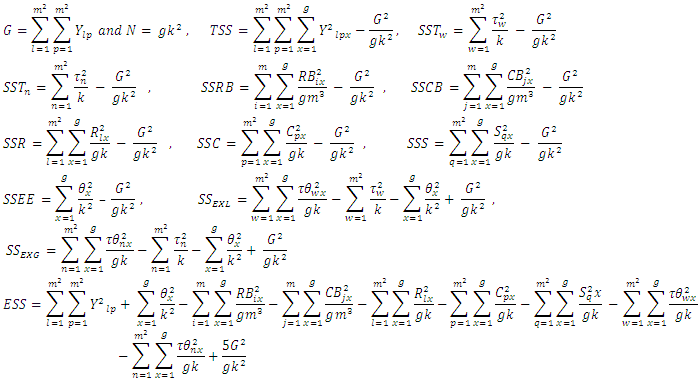
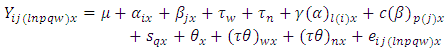 Where
Where 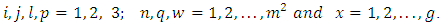 Where
Where 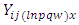 = Observation on experimental unit.
= Observation on experimental unit.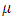 = Overall mean
= Overall mean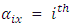 Row block effect in
Row block effect in 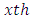 environment experiment,
environment experiment,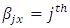 Column block effect in
Column block effect in 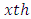 environment experiment,
environment experiment,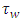 = Latin letter
= Latin letter 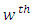 Treatment effect,
Treatment effect,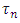 = Greek letter
= Greek letter 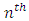 Treatment effect,
Treatment effect,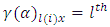 Row effect nested in
Row effect nested in 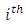 block (row) in
block (row) in 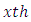 environment experiment,
environment experiment,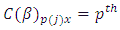 Column effect nested in
Column effect nested in 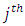 block (column) in
block (column) in 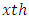 environment experiment,
environment experiment,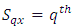 Sub-Square effect in
Sub-Square effect in 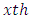 environment experiment,
environment experiment,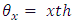 Environment-experiment,
Environment-experiment,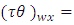 Interaction between
Interaction between 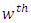 Latin Treatment and
Latin Treatment and 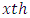 environment experiment,
environment experiment,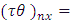 Interaction between
Interaction between 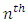 Greek Treatment and
Greek Treatment and 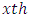 environment experiment,
environment experiment,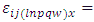 Error component with mean zero and variance
Error component with mean zero and variance 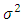
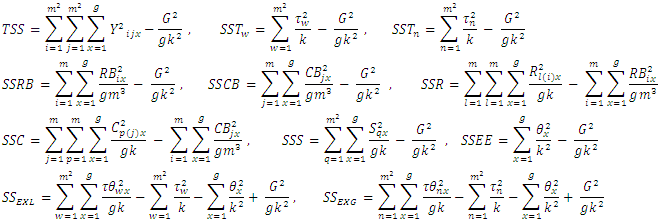
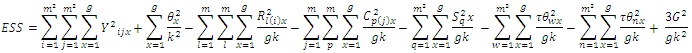
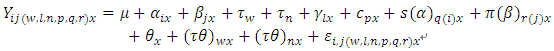 Where
Where 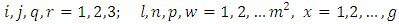 Where
Where 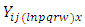 = Observation on experimental unit.
= Observation on experimental unit.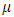 = Overall mean,
= Overall mean,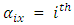 Row block effect in
Row block effect in 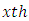 environment experiment,
environment experiment,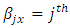 Column block effect in
Column block effect in 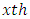 environment experiment,
environment experiment,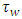 = Latin letter
= Latin letter 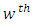 Treatment effect,
Treatment effect,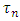 = Greek letter
= Greek letter 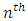 Treatment effect,
Treatment effect,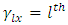 Row effect in
Row effect in 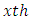 environment experiment,
environment experiment,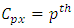 Row effect in
Row effect in 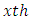 environment experiment,
environment experiment,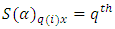 Row effect nested in
Row effect nested in 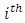 block (row) in
block (row) in 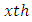 environment experiment,
environment experiment,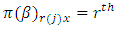 Column effect nested in
Column effect nested in 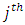 block (column) in
block (column) in 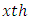 environment experiment,
environment experiment,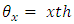 Environment-experiment,
Environment-experiment,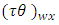 = Interaction between
= Interaction between 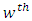 Latin Treatment and
Latin Treatment and 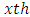 environment experiment,
environment experiment,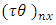 = Interaction between
= Interaction between 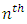 Greek Treatment and
Greek Treatment and 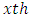 environment experiment,
environment experiment,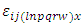 = Error component with mean zero and variance
= Error component with mean zero and variance 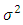
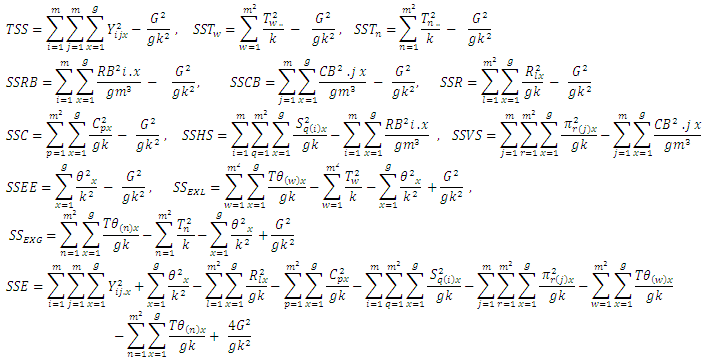
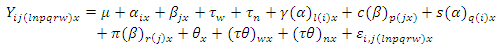 Where
Where 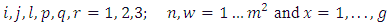 Where
Where 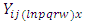 = Observation on experimental unit.
= Observation on experimental unit.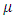 = General mean effect
= General mean effect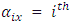 Row block effect in
Row block effect in 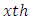 environment experiment,
environment experiment,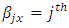 Column block effect in
Column block effect in 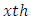 environment experiment,
environment experiment,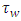 = Latin letter
= Latin letter 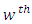 Treatment effect,
Treatment effect,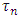 = Greek letter
= Greek letter 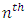 Treatment effect,
Treatment effect,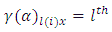 Row effect nested in
Row effect nested in 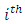 block (row) in
block (row) in 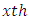 environment experiment,
environment experiment,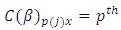 Column effect nested in
Column effect nested in 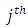 block (column) in
block (column) in 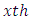 environment experiment,
environment experiment,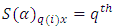 Horizontal Square effect nested in
Horizontal Square effect nested in 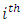 block (row) in
block (row) in 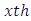 environment experiment,
environment experiment,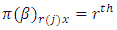 Vertical Square effect nested in
Vertical Square effect nested in 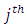 block (column) in
block (column) in 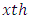 environment experiment,
environment experiment,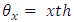 Environment-experiment,
Environment-experiment,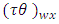 = Interaction between
= Interaction between 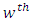 Latin Treatment and
Latin Treatment and 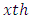 environment experiment,
environment experiment,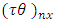 = Interaction between
= Interaction between 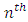 Greek Treatment and
Greek Treatment and 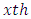 environment experiment,
environment experiment,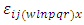 = Error component with mean zero and variance
= Error component with mean zero and variance 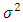
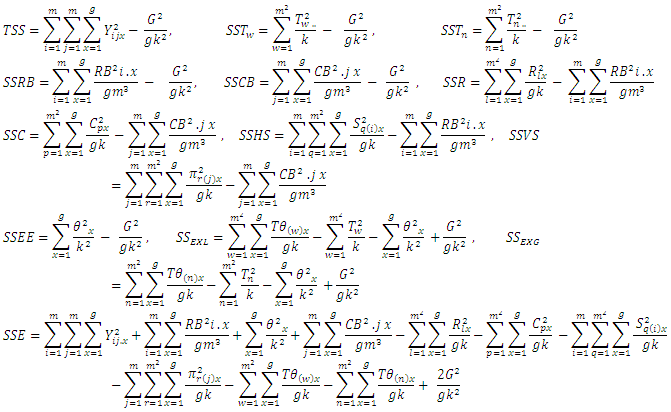
 obtained using orthogonal Sudoku square designs of order 9. Data for E1 are presented in [13] for analysis of single orthogonal Sudoku design. Combined ANOVA tables obtained using R software for models 1 to 4 are presented in tables 7 to 10, respectively.
obtained using orthogonal Sudoku square designs of order 9. Data for E1 are presented in [13] for analysis of single orthogonal Sudoku design. Combined ANOVA tables obtained using R software for models 1 to 4 are presented in tables 7 to 10, respectively. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML








