| [1] | Kernick, D. P., 2003, Introduction to health economics for the medical practitioner., Postgrad Med J, 79(929), 147-150. |
| [2] | Steinwachs, D. M. and Hughes, R. G., 2008, Health services research: Scope and significance. In R. G. Hughes (Ed.), Patient safety and quality: An evidence-based handbook for nurses, 1-163-1-177, Rockville (MD): Agency for Healthcare Research and Quality. |
| [3] | Tulchinsky, T. H. and Varavikova, E., 2009, The new public health, San Diego: Elsevier and Academic Press. |
| [4] | Mwabu, G., 2009, The demand for health care. In G. Carrin, H.K. Buse, K. Heggenhougen, and S.R. Quah, (Eds.), Health systems policy, finance and organization, 245-249, Oxford: Elsevier and Academic Press. |
| [5] | Earl, P. E. and Kemp, S., 1999, The Elgar companion to consumer research and economic psychology, Northampton: Edward Elgar Publishing, Inc. |
| [6] | Jack, W., 1999, Principles of health economics for developing countries. Washington: World Bank. |
| [7] | Gertler, P., Locay, L. and Sanderson, W., 1987, Are user fees regressive? The welfare implications of health care financing proposals in Peru., J Econom, 36(1-2), 67-88. |
| [8] | Cameron, A. C., Trivedi, P. K., Milne, F. and Pigott, J. A, 1988, Microeconomic model of the demand for health care and health insurance in Australia., Rev Econ Stud, 55(1), 85-106. |
| [9] | Rodriguez, M. and Stoyanova, A., 2004, The effect of private insurance access on the choice of GP/Specialist and public/private provider in Spain., Health Econ, 13(7), 689-703. |
| [10] | Dow, W. H., 1999, Flexible discrete choice demand models consistent with utility maximization: An application to health care demand., Am J Agric Econ, 81(3), 680-685. |
| [11] | Yip, W. C., Wang, H. and Liu, Y., 1998, Determinants of patient choice of medical provider, A case study in rural China., Health Policy Plan, 3(3), 311-322. |
| [12] | Hensher, D.A. and Johnson, L.W., 1981, Applied discrete choice modeling. New York: John Wiley & Sons, Inc. |
| [13] | Orturaz, J. dD. and Willumsen, L. G., 2001, Modelling Transport. West Sussex: John Wiley & Sons, Inc. |
| [14] | Penchansky, R. and Thomas, J. W., 1981, The concept of access: definition and relationship to consumer satisfaction., Med Care, 19(2), 127-140. |
| [15] | O'Donnell, Ο, Van Doorslaer, E., Wagstaff, A. and Lindelow, M., 2007, Analyzing health equity using household survey data: A guide to techniques and their implementation. Washington DC: World Bank. |
| [16] | Jones, A. M., 2006, The Elgar companion to health economics, Northampton: Edward Elgar Publishing, Inc. |
| [17] | Train, K., 2003, Discrete choice methods with simulation. Cambridge: Cambridge University Press. |
| [18] | Cascetta, E., 2009, Transportation systems analysis: Models and applications. New York: Springer. |
| [19] | Hensher, D. A., Rose, J. M. and Greene, W. H., 2005, Applied choice analysis: A primer. Cambridge: Cambridge University Press. |
| [20] | Anderson, D. R., Sweeney, D. J., Williams, T. A, Camm, J. D. and Cochran, J.J., 2015, Essentials of statistics for business and economics. Stamford: Cengage Learning. |
| [21] | Agresti, A., 2002, Categorical data analysis. New Jersey: John Wiley and Sons, Inc. |
| [22] | Folz, D. H., 1996, Survey research for public administration. London: SAGE. |
| [23] | de Gruijter, J., Brus, D., Bierkens M. and Knotters, M., 2006, Sampling of natural resource monitoring. New York: Springer. |
| [24] | Üstün, T.B., Chatterji, S., Villanueva, M., Bendib, L., Çelik, C., Sadana, R., Valentine, N., Ortiz, J., Tandon, A., Salomon, J., Cao, Y., Wan Jun, X., Özaltin, E., Mathers, C. and Murray, C. J. L., 2001, WHO multi-country survey study on health and responsiveness 2000-2001, GPE Discussion Paper 37 http://www.who.int/healthinfo/survey/whspaper37.pdf. |
| [25] | Mosialos, E., Allin, S. and Davaki, K., 2005, Analysing the Greek health system: A tale of fragmentation and inertia., Health Econ., 14, S151-S168. |
| [26] | Kyriopoulos, J., Lionis, C., Dimoliatis, I., Merkouris, B. P., Oikonomou, C., Tsakos, G. and Philalithis, A. and Working Group: Antonakis, N., Georgoussi, E., Dolgeras, L., Domenikos, C., Zavras, Th., Kontos, D., Kounari, C., Beazoglou, T., Boursanidis, C., Symeonidis, S., Souliotis, K., Tsalikis, G., Vasilikiotis, N., Vrachni, Tz., 2000, Primary health care as a cornerstone for health reform in Greece., Primary Health Care, 12(4), 169-188 (in Greek). |
| [27] | Filzmoser, P., Hron, K.and Reimann, C., 2009, Univariate statistical analysis of environmental (compositional) data: Problems and possibilities., Sci Total Environ, 407(23), 6100-61088. |
| [28] | Aitchison, J., 1986, The Statistical analysis of compositional data. New York: Chapman & Hall. |
| [29] | Smithson, M. and Verkuilen, J., 2006, A better lemon squeezer? Maximum likelihood regression with beta-distributed dependent variables., Psychol Methods, 11(1), 54-71. |
| [30] | Ferrari, S. and Cribari-Neto, F., 2004, Beta regression for modelling rates and proportions., J Appl Stat, 31(7), 799-815. |
| [31] | Cook, A. A. Jr., 1971, A note on estimating proportions by linear regressions. Santa Monica: RAND. |
| [32] | Papke, L. E. and Wooldridge, J. M., 1996, Econometric methods for fractional response variables with application to 401(K) plan participation rates., J Appl Econ, 11(6), 619-632. |
| [33] | Aitchison, J., 1982, The statistical analysis of compositional data., J R Stat Soc Series B Stat Methodol, 44(2), 139-177. |
| [34] | Kieschnick, R. and McCullough, B. D., 2003, Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions., Stat Modelling, 3(3), 193-213. |
| [35] | Cohen, J., Cohen, P., West, S. G. and Aiken, L. S., 2003, Applied multiple regression/correlation analysis for the behavioral sciences. New Jersey: Lawrence Erlbaum Associates. |
| [36] | Crown, W. H., 1998, Statistical models for the social and behavioral sciences: multiple regression and limited dependent variable models. Westport CT: Praeger Publishers. |
| [37] | Billheimer, D., 2002, Compositional data. In A. H. El-Shaarawi, and W.W. Piegorsch (Eds.), Encyclopedia of Environmetrics Vol. 1, 391-399, Chichester: John Wiley and Sons, Inc. |
| [38] | Lipsmeyer, C. S., Philips, A. Q., Rutherford, A. and Whitten, G. D., 2017, Comparing dynamic pies: A strategy for modeling compositional variables in time and space., Political Science Research and Methods, 1-18. |
| [39] | Katz, J.N. and King, G., 1999, A statistical model for multiparty electoral data., Am Polit Sci Rev, 93(1), 15-32. |
| [40] | Tsagris, M., Preston, S. and Wood, A. T. A., 2016, Improved classification for compositional data using the α-transformation., J Classif, 33(2), 243-261. |
| [41] | Tsagris, M., 2015, Regression analysis with compositional data containing zero values., Chil J Stat, 6(2), 47-57. |
| [42] | Steinskog, D. J., Tjøstheim, D. B. and Kvamstø, N. G., 2007, A cautionary note on the use of the Kolmogorov-Smirnov test for normality., Mon. Wea. Rev., 135, 1151-1157. |
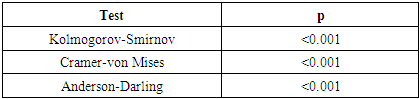
| [43] | Adhikari, S. R., 2011, A methodological review of demand analysis: an example of health care services., EJDI, 13 & 14(1-2), 119-130, Combined Issue. |
| [44] | Rani, M. and Bonu, S., 2003, Rural Indian women’s care-seeking behavior and choice of provider for gynecological symptoms., Stud Fam Plann, 34(3), 173-185. |
| [45] | Habtom, G. K. and Ruys, P., 2007, The choice of health care provider in Eritrea., Health Policy, 80, 202-217. |
| [46] | Lim, M-K., Yang, H., Zhang, T., Feng, W. and Zhou, Z., 2004, Public perceptions of private health care in socialist China., Health Aff (Millwood), 23(6), 222-234. |
| [47] | Ha, N. T. H., Berman, P. and Larsen, U., 2002, Household utilization and expenditure on private and public health services in Vietnam., Health Policy and Plan, 17(1), 61-70. |
| [48] | Castiglione, D., Lovasi, G. S. and Carvalho, M., S., 2017, Perceptions and uses of public and private health care in a Brazilian Favela., Qual Health Res 00(0), 1-14. |
| [49] | Amaghionyeodiwe, L. A., 2018, Poverty, user charges and health care demand in Nigeria., IJBED, 6(2), 37-50. |
| [50] | Gerdtham, Ulf. G. and Jönsson, B., 1991, Price and quantity in international comparisons of health care expenditure., Appl Econ, 23, 1519-1528. |
| [51] | Winkelmann, R., 2008, Econometric analysis of count data. New York: Springer. |
| [52] | McClellan Buchanan, G., Rubenstein Gardenswartz, C. A. and Seligman, M. E. P., 1999, Physical health following a cognitive-behavioral intervention., Prevention and Treatment, 2, Article 10. |
| [53] | Hess, S. and Daly, A., 2014, Handbook of choice modelling. Northhampton: Edward Elgar. |
| [54] | Paolino, P., 2001, Maximum likelihood estimation of models with beta-distributed dependent variables., Polit Anal, 9(4), 325-346. |
| [55] | Woodland, A. D., 1979, Stochastic specification and the estimation of share equations., J Econom, 10(3), 361-383. |
| [56] | McDonald, J., 2009, Using least squares and tobit in second stage DEA efficiency analyses., Eur J Oper Res, 197(2), 792-8. |
| [57] | Hoff, A., 2007, Second Stage DEA: Comparison of approaches for modelling the DEA score., Eur J Oper Res, 181(1), 425-435. |
| [58] | Ranganathan, Y. and Borges, R. M., 2011, To transform or not to transform: That is the dilemma in the statistical analysis of plant volatiles. Plant Signal Behav, 6(1), 113-116. |
| [59] | Hossain, A, Rigby, R., Stasinopoulos, M. and Enea, M., 2016, Centile estimation for a proportion response variable., Statist. Med., 35, 895-904. |




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML