-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2018; 8(5): 267-273
doi:10.5923/j.statistics.20180805.05

Coset-k2 Nested Balanced Incomplete Block Designs of Resolvable Type
A. J. Saka1, B. L. Adeleke2, T. G. Jaiyeola1
1Department of Mathematics, Obafemi Awolowo University, Ile Ife, Nigeria
2Department of Statistics, University of Ilorin, Ilorin, Nigeria
Correspondence to: A. J. Saka, Department of Mathematics, Obafemi Awolowo University, Ile Ife, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper presents, a new method of constructing nested balanced incomplete block designs (NBIBDs) of resolvable type called Coset-k2, using an algebraic notion, of the left coset type. The class of NBIBDs that was constructed for 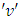 treatments arranged in ‘b’ blocks of size
treatments arranged in ‘b’ blocks of size 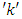 each with
each with 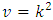 and other parameters of the design are expressed as
and other parameters of the design are expressed as 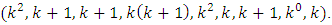 Indeed, the parameters of the design for any given number of treatments, v, are specified with ease even before the full designs are constructed. Also, fewer numbers of blocks are required when compared with the designs of comparable sizes. Designs that are constructed in this paper are appropriate for experiments where extraneous factors of two types if they exist can be eliminated, evaluated and controlled.
Indeed, the parameters of the design for any given number of treatments, v, are specified with ease even before the full designs are constructed. Also, fewer numbers of blocks are required when compared with the designs of comparable sizes. Designs that are constructed in this paper are appropriate for experiments where extraneous factors of two types if they exist can be eliminated, evaluated and controlled.
Keywords: Coset, Resolvable Designs, Incomplete Block Designs, Nested Designs and Nested Balanced Incomplete Block Designs
Cite this paper: A. J. Saka, B. L. Adeleke, T. G. Jaiyeola, Coset-k2 Nested Balanced Incomplete Block Designs of Resolvable Type, International Journal of Statistics and Applications, Vol. 8 No. 5, 2018, pp. 267-273. doi: 10.5923/j.statistics.20180805.05.
Article Outline
1. Introduction
- Some experimental material, may exhibit more than one source of variation that can be controlled by ordinary blocking and there may also be other types of relationships among several types of variation. A relationship that is often encountered in practice and which is of concern in this paper is nesting between two or more set of blocks. Example1 and 2 that utilised nesting relation are provided below as real life Animal and Plant experiments.Example 1 (Plant Experiment) Preece [17], illustrated nesting, such that the half-leaves of a plant form the experimental units, on which a number of treatments were to be tested, where the number of treatments is more than the number of available half-leaves per plant. Clearly, one source of variation is due to variability among the plants. Further, leaves within a plant might exhibit variation due to their location on the upper, middle or lower branch of the same plant. Therefore, leaves within plants are nested nuisance factor, the nesting being within the plants. The half-leaves being the experimental units, there are two systems of blocks, leaves (which may be called sub-blocks) being nested within plants. Example 2 (Animal Experiment) Generally littermates, or (animals born in the same day) are experimental units within a block. However, animals within the same litter may be varying in their initial body weight. If body weight is taken as another blocking factor, we have a system of nested blocks within a block. More examples and discussion of nesting, can be found in the literature, see for example Srivastana [20] and Morgan [13]Definition 1 A NBIBD with parameters (v, r, b1, b2, k1, k2, λ1, λ 2, m) is an incomplete block design with v treatments, each replicated r times, within two systems of blocks such that:i. the second system is nested within the first, with each block from the first system (called blocks) containing exactly m blocks of the second system (called sub-blocks);ii. ignoring the sub-blocks leaves a BIB design with parameters v, b1, r, k1, λ 1; and iii. ignoring the blocks leaves a BIB design with parameters v, b2, r, k2, λ 2 Theorem 1 Jimbo and Kuriki [11]. Consider a BIBD with parameters v*, b*, k* = v and also a BIBD design with (v, b1, b2, k), if the NBIBD is written using the treatments of each block of the BIB design, then the resulting design is a NBIB (v*, b1b*, b2, k).A BIBD is resolvable (Abel and Furino [1]) and Bailey [2], if its set of blocks can be partitioned into subsets such that each subset is a replicate or resolution class, such that each subset contains each treatment exactly once. Remark, a resolvable incomplete block design is a special case of nested incomplete block designs, with the main blocks being complete. In view of this fact, if a resolvable BIB design is taken as a particular case of NBIB design in Theorem 2, and the NBIB design wherein is the same as ones obtained by Dey et. al. [7]. NBIB designs has been studied by a number of other authors, including Preece [17], Jimbo and Kuriki [11], Bailey [3], Iqbal [9], Jimbo [10], Jimbo and Kuriki [11] and Dey et. al. [5]Theorem 2 The existence of a NBIB design (v, b1, b2, k) and of a resolvable BIB design with parameters v* = b2, b*, k* implies the existence of a NBIB (v, b1b*, k*, k).
2. Method of Construction
- In recent time, the development of the theory of designs has continued to exploit the advantages of advanced topics in algebra and combinatorics. Wen-Fong and Gunter [22] has shown how some specific classes of algebraic structures (planar near rings) give rise to efficient balanced incomplete block designs. Also, Morgan et al. [14], reviewed and extended mathematical aspect of nested balanced incomplete block design (NBIBD’s); isomorphism and automorphisms were defined for NBIBDs, and methods of construction were outlined. Peter, et al. [16], showed the necessary divisibility conditions for the existence of a 𝜎-resolvable BIBD (v, k, ʎ) as sufficient for large v. Saka et al. [19], developed a new method of construction of nested balanced incomplete block designs in which the resulting design schemes were of the type that harmonizes both the Series-I and Series-II of Rajender et al. [18]. Keerti and Vineeta [12], introduced a new method of construction of a series of Nested Balanced Incomplete Block Designs (NBIBDs) in which the inner blocks are constructed using Latin square. In this paper we present a new method of constructing NBIB designs called Coset-k2 of NBIB designs of resolvable type using an algebraic notion (left coset).
2.1. Reduced BIBD
- The simplest series of balanced incomplete block designs is unreduced BIBDs. These designs consist of all possible combinations of k out of v treatments. Balanced incomplete block designs exist for a wide range of design parameters. The basic design parameters are (v, b, k) which denote number of treatments, number of blocks and block size respectively. However, the only disadvantage it has is that in some cases, the size of experiment might be too large to work with in real life. When the number of treatments, v, is a perfect squares with v ≥ 9 and k < v the number of blocks required could be too large to cope with. This may force the experiment to adopt the reduced BIBDs. As such the reduced method is demonstrated in the construction of Designs 2, 3, 4 in section 4.3. Consequently, for instance, the design of unreduced BIBDs can be reduced by finding the highest common factor (H.C.F) of the parameters (b, r, λ) provided the value of H.C.F is neither decimal nor unity. The corresponding reduced designs could be obtained as: b1 = b/f, r1 = r/f, λ1 = λ /f, where (b1, r1, λ1) represents the parameters of the new (reduced) design and f is the H.C.F. of the parameters (b, r, λ). Example 3 and 4 below are to show the extent of reduction in the size of experiments that can be achieved with the use of reduced BIBD. Example 3 Let us consider an unreduced design for case v =7 and k = 3, the design is given by the following 35 blocks:
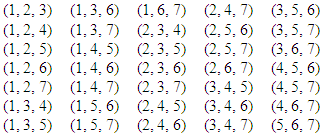 The parameters of the design are:v = 7, k = 3, b = 35, r = 15, λ = 5.The corresponding reduced BIBD of example 3 is as presented as example 4 below: Example 4 Reduced BIBD from unreduced BIBD in Example 3:(1, 2, 4)(1, 3, 7)(1, 5, 6)(2, 3, 5)(2, 6, 7)(3, 4, 5)(4, 5, 7)The parameters of the resulting reduced design are:v = 7, k = 3, b1 = 7, r1 = 3, λ1 = 1which satisfies the necessary conditions for the existence of BIBDs.
The parameters of the design are:v = 7, k = 3, b = 35, r = 15, λ = 5.The corresponding reduced BIBD of example 3 is as presented as example 4 below: Example 4 Reduced BIBD from unreduced BIBD in Example 3:(1, 2, 4)(1, 3, 7)(1, 5, 6)(2, 3, 5)(2, 6, 7)(3, 4, 5)(4, 5, 7)The parameters of the resulting reduced design are:v = 7, k = 3, b1 = 7, r1 = 3, λ1 = 1which satisfies the necessary conditions for the existence of BIBDs.2.2. Some Definitions, Basic Mathematical Concepts and Assumptions
- Here, some mathematical terminologies, as well concepts, such as equivalence relations and partitions and some assumptions for the Coset-k2 NBIBD of resolvable type, will be defined.(a) Definition of Terms: Two terms namely, left and right cost; and coset as Initial block will be defined in what follows:Definition 2 (Left and Right Coset) Let G be a group, and H a subgroup of G, and g an element of G. ThengH = {gh : h is an element of H} is called a left coset of H in G, by g andHg = {hg : h is an element of H} is called a right coset of H in G by g. If K = gh = Hg, then K is called a coset of H in G by g. Definition 3 (Coset as Initial Block) Let H ≤ G. The quotient set G / H = {gH : g ϵ G} is called the Coset initial Block of H in G if G / H partitions G. A NBIBD of resolvable type with G / H as coset initial block is called a Coset-|H|2 or Coset-|G| NBIBD of resolvable type.(b) Concepts of Equivalence Relation and PartitionsHere, the concepts of Equivalence Relations and Partitions are presented because of their relevance in the proof of Theorem 5. Let A and B be sets. Subsets of A x B are called relations. An equivalence relation on a set X is a relation R ϲ X × X such thati. (x, x) ϵ R for all x ϵ X (reflexive property);ii. (x, y) ϵ R implies (y, x) ϵ R (symmetric property);iii. (x, y), (y, z) ϵ R imply (x, z) ϵ R (transitive property);A partition P of a set X is a collection of non-empty sets Xi, i ϵ Ω such that Xi ∩ Xj = ϕ for i ≠ j and.
 Let R be an equivalence relation on a set X and let x ϵ X. Then [x] = {y ϵ X : yRx} is called the equivalence class of x.Theorem 3 Fundamental Theorem of Equivalence Relation Given an equivalence relation R on a set X, the equivalence classes of X form a partition of X. Conversely, if P = {Xi}iϵΩ is a partition of a set X, then there is an equivalence relation on X with equivalence classes Xi.
Let R be an equivalence relation on a set X and let x ϵ X. Then [x] = {y ϵ X : yRx} is called the equivalence class of x.Theorem 3 Fundamental Theorem of Equivalence Relation Given an equivalence relation R on a set X, the equivalence classes of X form a partition of X. Conversely, if P = {Xi}iϵΩ is a partition of a set X, then there is an equivalence relation on X with equivalence classes Xi. 3. Theorems and Lemma for Construction of Designs
- This section shall present a number of theorems to facilitate the design construction, and four assumptions that are to be compiled with are as follows:1. v, number of treatments must be perfect square; and that v = k2, where k is the size of the block; 2. if two treatments occur together in one sub-block, they must not occur together again in the subsequent sub-blocks throughout the construction of the designs;3. number of main-blocks is k + 1; and 4. number of sub-blocks is k(k + 1)Lemma 1 For a coset resolvable NBIBD with parameters
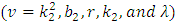 satisfy the following relation.
satisfy the following relation.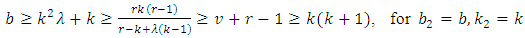 | (1) |
3.1. Theorems on Coset-k2 of NBIBD of Resolvable Type
- Theorem 4 Let
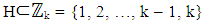 be a sub-block (generator) defined as H = {nk \ n = 1,…, k}, then i + H = {(i+h)(mod v)lh ϵ H}, i = 1, … k, with v( mod) = v, where k2, is called a coset of H in ℕ by i ϵ N. The family {i + H}ki=1 is called the coset initial block of H in N. Let
be a sub-block (generator) defined as H = {nk \ n = 1,…, k}, then i + H = {(i+h)(mod v)lh ϵ H}, i = 1, … k, with v( mod) = v, where k2, is called a coset of H in ℕ by i ϵ N. The family {i + H}ki=1 is called the coset initial block of H in N. Let 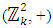 be the group of integers modulo k2,
be the group of integers modulo k2, 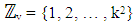 with a subgroup H = {nk n = 1, 2,…, k}. Then(i)
with a subgroup H = {nk n = 1, 2,…, k}. Then(i) 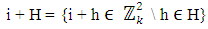 is a coset of H in
is a coset of H in 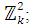 (ii)
(ii) 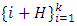 is a Coset Initial Block of H in
is a Coset Initial Block of H in 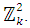 Proof: For k = 2,3,4 are illustrated below in cases 1,2 and 3 respectively.
Proof: For k = 2,3,4 are illustrated below in cases 1,2 and 3 respectively.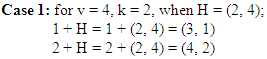 The initial main-block for NBIBD for v = 4, k = 2, is [(3, 1), (4, 2)].
The initial main-block for NBIBD for v = 4, k = 2, is [(3, 1), (4, 2)]. 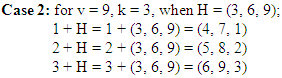 The initial main-block for NBIBD for v = 9, k = 3, is [(4, 7, 1), (5, 8, 2), (6, 9, 3)].
The initial main-block for NBIBD for v = 9, k = 3, is [(4, 7, 1), (5, 8, 2), (6, 9, 3)].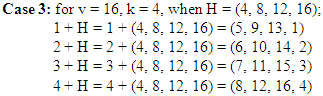 The initial main-block for NBIBD for v = 16, k = 4, is [(5, 9, 13, 1), (6, 10, 14, 2), (7, 11, 15, 3), (8, 12, 16, 4)].Case 4: Let k = m, v = [1, 2, …, m2], H = {mn : n = 1, …, m} = {m, 2m, 3m, …, (m – 5)m, (m – 4)m, (m – 3)m, (m – 2)m, (m – 1)m, m2}. The sub-blocks which form the initial main-block are shown in Figure 1.Case 5: Consider k = m + 1, v = [1, 2, …, (m + 1)2], H = {(m + 1)n : n = 1, …, m + 1} = {m + 1, 2(m + 1), 3(m + 1), …, (m - 1)(m + 1), m(m + 1), (m + 1)2}. The sub-blocks which form the initial main-block are shown in Figure 2.The entries in the matrix in Figure 1 marked with a unique colour in diagonal lines correspond with entries in the matrix in Figure 2 marked with the same unique colour of horizontal lines in the appropriate direction of sequence. Entries in the last column of the matrix in Figure 1 correspond to the entries in the last column of matrix in Figure 2, except the entry
The initial main-block for NBIBD for v = 16, k = 4, is [(5, 9, 13, 1), (6, 10, 14, 2), (7, 11, 15, 3), (8, 12, 16, 4)].Case 4: Let k = m, v = [1, 2, …, m2], H = {mn : n = 1, …, m} = {m, 2m, 3m, …, (m – 5)m, (m – 4)m, (m – 3)m, (m – 2)m, (m – 1)m, m2}. The sub-blocks which form the initial main-block are shown in Figure 1.Case 5: Consider k = m + 1, v = [1, 2, …, (m + 1)2], H = {(m + 1)n : n = 1, …, m + 1} = {m + 1, 2(m + 1), 3(m + 1), …, (m - 1)(m + 1), m(m + 1), (m + 1)2}. The sub-blocks which form the initial main-block are shown in Figure 2.The entries in the matrix in Figure 1 marked with a unique colour in diagonal lines correspond with entries in the matrix in Figure 2 marked with the same unique colour of horizontal lines in the appropriate direction of sequence. Entries in the last column of the matrix in Figure 1 correspond to the entries in the last column of matrix in Figure 2, except the entry 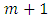 in the last row; which corresponds to the entry in the row 1, column 1 of the matrix in Figure 1. All entries in the matrix of Figure 1 can be found in the matrix of Figure 2. However, the converse is not true because entries in the third and second to the last columns (except one entry
in the last row; which corresponds to the entry in the row 1, column 1 of the matrix in Figure 1. All entries in the matrix of Figure 1 can be found in the matrix of Figure 2. However, the converse is not true because entries in the third and second to the last columns (except one entry 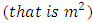 ) of the matrix in Figure 2 are not in the matrix in the Figure 1. These entries are
) of the matrix in Figure 2 are not in the matrix in the Figure 1. These entries are 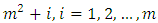 and
and 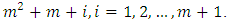 All these entries are distinct and greater than
All these entries are distinct and greater than 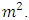 Thus, when
Thus, when 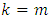 we have a Coset Initial Block of
we have a Coset Initial Block of 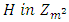 . So, when
. So, when 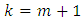 we equally have a Coset Initial Block of
we equally have a Coset Initial Block of 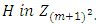
 | Figure 1. Proof of Theorem 4 for k=m |
 | Figure 2. Proof of Theorem 4 for k = m+1 |
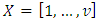 be a given treatment
be a given treatment 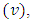 and let
and let 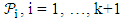 be partitions of X such that for the sub blocks
be partitions of X such that for the sub blocks 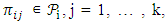
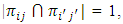
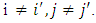 Then
Then 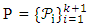 is a Nested Balanced Incomplete Block Designs (NBIBD) of resolvable type with; treatment
is a Nested Balanced Incomplete Block Designs (NBIBD) of resolvable type with; treatment 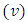 , sub-block size
, sub-block size 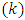 and parameter combinations
and parameter combinations 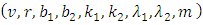
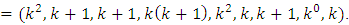 Proof: Consider the pair
Proof: Consider the pair 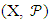 where X = {1, 2, …, K2} and
where X = {1, 2, …, K2} and 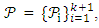 such that
such that 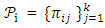 is a partition of X for each
is a partition of X for each 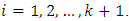 Consider the pair
Consider the pair 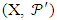 where
where 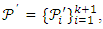 such that
such that 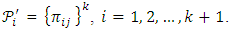
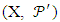 is a block design because X is a set of elements called points and
is a block design because X is a set of elements called points and 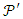 is a collection of non-empty subsets
is a collection of non-empty subsets 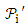 of 2X called blocks. Since
of 2X called blocks. Since 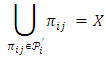 for each
for each 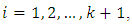 then
then 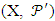 is a complete block design with
is a complete block design with 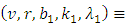
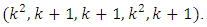 Consider the pair
Consider the pair 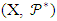 where X = {1, 2, …, k2} and
where X = {1, 2, …, k2} and 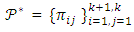 .
. 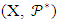 is a block design because
is a block design because 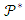 is a collection of non-empty subset
is a collection of non-empty subset 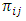 ,
, 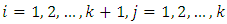 of X called sub-blocks. Recall that
of X called sub-blocks. Recall that 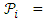
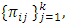 partitions X for each
partitions X for each 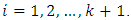 This implies
This implies 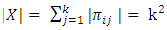 for each
for each 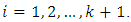 Thus,
Thus, 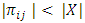 for each
for each 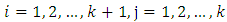 i.e
i.e 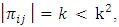 hence,
hence, 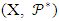 is an Incomplete Block Design. Also, since
is an Incomplete Block Design. Also, since 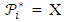 for each
for each 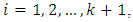
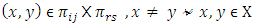 appears once for
appears once for 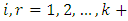
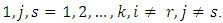 That is the numbers of pair of treatments is one (λ = 1). Thus,
That is the numbers of pair of treatments is one (λ = 1). Thus,  is a BIBD with
is a BIBD with 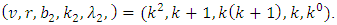 Since
Since 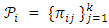 partition X for each
partition X for each 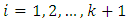 distinctly, then if
distinctly, then if 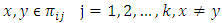 then
then 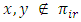
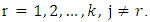 Let
Let  be the equivalence relation corresponding to partition
be the equivalence relation corresponding to partition 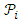 based on Theorem 3, then
based on Theorem 3, then 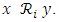 Consider another partition
Consider another partition 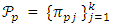 of X. If
of X. If 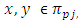
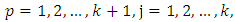 then
then 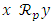 and so
and so 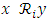 and
and 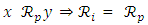 i.e
i.e 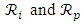 are not disjoint which is a contradiction. Thus
are not disjoint which is a contradiction. Thus 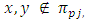 whereas
whereas 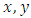
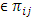 for any
for any 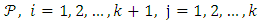 . Hence, the pair
. Hence, the pair 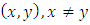 , appears once whereas
, appears once whereas 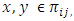
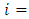
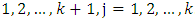 . So,
. So, 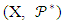 is a BIBD. Now, the Nested Block design
is a BIBD. Now, the Nested Block design 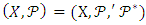 is a Nested Balanced Incomplete Block Design (NBIBD) of a Resolvable type with parameters
is a Nested Balanced Incomplete Block Design (NBIBD) of a Resolvable type with parameters 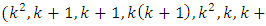
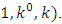 Theorem 6: Let
Theorem 6: Let 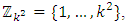
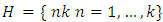 and let
and let 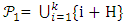 modulo k2 with
modulo k2 with 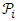 , i = 2, …, k+1 as partitions of
, i = 2, …, k+1 as partitions of 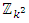 such that for the blocks
such that for the blocks 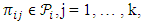
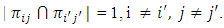 Then
Then 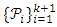 is a Coset-k2 Nested Balanced Incomplete Block Designs (NBIBD) of Resolvable type with block size
is a Coset-k2 Nested Balanced Incomplete Block Designs (NBIBD) of Resolvable type with block size 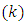 and treatment
and treatment 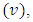 with parameters
with parameters 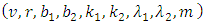
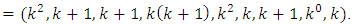 Proof: This is achieved by using Theorem 4 and Theorem 5. By Theorem 4,
Proof: This is achieved by using Theorem 4 and Theorem 5. By Theorem 4, 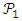 is a partition of X and so by Theorem 5,
is a partition of X and so by Theorem 5, 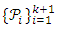 is a
is a 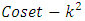 Nested Balanced Incomplete Block Designs (NBIBD) of Resolvable type with block size
Nested Balanced Incomplete Block Designs (NBIBD) of Resolvable type with block size 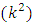 and treatment
and treatment 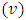 , With parameters
, With parameters 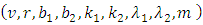
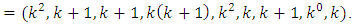
4. Construction of Designs
- Here, nested balanced incomplete block designs for a number of parameter combinations will be constructed. In what immediately, appropriate model and relationship between design parameters shall be presented.
4.1. Model Specification
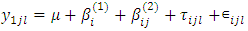 | (2) |
4.2. Relationship between Design Parameters
- First, the design parameters are stated and defined as follow:
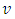 denotes the number of treatments, b number of blocks in the experiment, k size of each block (number of treatment per block), r number of replications for a given treatment in the experiment, λ number of times each pair of treatment appear (occur) together in the experiment, N total number of plots (observations), b1 number of main-blocks in the experiment, b2 number of sub-blocks in the experiment, k1 size of each main-block (number of treatment per main-block), k2 size of each sub-block (number of treatment per sub-block), λ1 number of times each pair of treatment appear (occur) together in the main-blocks, λ2 number of times each pair of treatment appear (occur) together in the sub-blocks and m number of sub-blocks within the main block.Meanwhile, the relationships among the design parameters given above are presented below.
denotes the number of treatments, b number of blocks in the experiment, k size of each block (number of treatment per block), r number of replications for a given treatment in the experiment, λ number of times each pair of treatment appear (occur) together in the experiment, N total number of plots (observations), b1 number of main-blocks in the experiment, b2 number of sub-blocks in the experiment, k1 size of each main-block (number of treatment per main-block), k2 size of each sub-block (number of treatment per sub-block), λ1 number of times each pair of treatment appear (occur) together in the main-blocks, λ2 number of times each pair of treatment appear (occur) together in the sub-blocks and m number of sub-blocks within the main block.Meanwhile, the relationships among the design parameters given above are presented below. 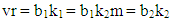 | (3) |
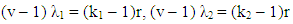 | (4) |
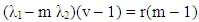 | (5) |
4.3. Nested BIBD’s for v = 4, 9, 16, and 25
- Here, Theorem 4, Theorem 5, and Theorem 6 were continuously utilized for the construction of designs 1 to 6 for v = 4, v = 9 and v = 16 respectively. Design 1: A resolvable NBIB Design v = 4, k = 2 [(3, 1),(4, 2)][(3, 4)(1, 2)][(1, 4),(2, 3)]The parameters of the design are:v = 4, r = 3, b1 = 3, k1 = 4, λ1 = 3, b2 = 6, k2 = 2, λ2 = 1Design 2: A resolvable NBIB Design v = 9, k = 3
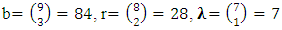 The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 7, thenb1 = b/f = 84/7 = 12, r1 = r/f = 28/7 = 4, λ1 = λ /f = 7/7 = 1[(4, 7, 1), (5, 8, 2), (6, 9, 3)][(4, 5, 6), (7, 8, 9,),(1, 2, 3)][(1, 6, 8), (2, 4, 9), (3, 5, 7)][(1, 5, 9), (2, 6, 7), (3, 4, 8)]The parameters of the design are:V = 9, r = 4, b1 = 4, k1 = 9, λ1 = 4, b2 = 12, k2 = 3, λ2 = 1Design 3: A resolvable NBIB design v = 16, k = 4
The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 7, thenb1 = b/f = 84/7 = 12, r1 = r/f = 28/7 = 4, λ1 = λ /f = 7/7 = 1[(4, 7, 1), (5, 8, 2), (6, 9, 3)][(4, 5, 6), (7, 8, 9,),(1, 2, 3)][(1, 6, 8), (2, 4, 9), (3, 5, 7)][(1, 5, 9), (2, 6, 7), (3, 4, 8)]The parameters of the design are:V = 9, r = 4, b1 = 4, k1 = 9, λ1 = 4, b2 = 12, k2 = 3, λ2 = 1Design 3: A resolvable NBIB design v = 16, k = 4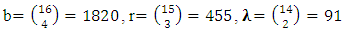 The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 91, thenb1 = b/f = 1820 / 91 = 20, r1 = r / f = 455/91 = 5,λ1 = λ /f = 91/91 = 1[(5, 9, 13, 1), (6, 10, 14, 2), (7, 11, 15, 3), (8,12 , 16, 4)][(5, 6, 7, 8), (9, 10, 11, 12), (13, 14, 15, 16), (1, 2, 3, 4)][(1, 6, 11, 16), (2, 5, 12, 15), (3, 8, 9, 14), (4, 7, 10, 13)][(1, 7, 12, 14), (2, 8, 11, 13), (3, 5, 10, 16), (4, 6, 9, 15)][(1, 8, 10, 15), (2, 7, 9, 16), (3, 6, 12, 13), (4, 5, 11, 14)]The parameters of the design are:v = 16, r = 5, b1 = 5, k1 = 16, λ1 = 5, b2 = 20, k2 = 4, λ2 = 1Design 4: A resolvable NBIB design v= 25, k = 5
The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 91, thenb1 = b/f = 1820 / 91 = 20, r1 = r / f = 455/91 = 5,λ1 = λ /f = 91/91 = 1[(5, 9, 13, 1), (6, 10, 14, 2), (7, 11, 15, 3), (8,12 , 16, 4)][(5, 6, 7, 8), (9, 10, 11, 12), (13, 14, 15, 16), (1, 2, 3, 4)][(1, 6, 11, 16), (2, 5, 12, 15), (3, 8, 9, 14), (4, 7, 10, 13)][(1, 7, 12, 14), (2, 8, 11, 13), (3, 5, 10, 16), (4, 6, 9, 15)][(1, 8, 10, 15), (2, 7, 9, 16), (3, 6, 12, 13), (4, 5, 11, 14)]The parameters of the design are:v = 16, r = 5, b1 = 5, k1 = 16, λ1 = 5, b2 = 20, k2 = 4, λ2 = 1Design 4: A resolvable NBIB design v= 25, k = 5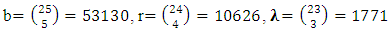 The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 1771, thenb1 = b/f = 53130/1771 = 30, r1 = r/f = 10626/1771 = 6, λ1 = λ /f = 1771/1771 = 1 [(6, 11, 16, 21, 1), (7, 12, 17, 22, 2), (8, 13, 18, 23, 3), (9, 14, 19, 24, 4), (10, 15, 20, 25, 5)][(6, 7, 8, 9, 10), (11, 12, 13, 14, 15), (16, 17, 18, 19, 20), (21, 22, 23, 24, 25), (1, 2, 3, 4, 5)][(1, 7, 13, 19, 25), (2, 10, 14, 16, 23), (3, 9, 12, 20, 21), (4, 6, 15, 18, 22), (5, 8, 11, 17, 24)][(1, 8, 14, 20, 22), (2, 9, 11, 18, 25), (3, 7, 15, 16, 24), (4, 10, 13, 17, 22), (5, 6, 12, 19, 23)][(1, 9, 15, 17, 23), (2, 6, 13, 20, 24), (3, 10, 11, 19, 22), (4, 8, 12, 16, 25), (5, 7, 14, 18, 21)][(1, 10, 12, 18, 24), (2, 8,15, 19, 21), (3, 6, 14, 17, 25), (4, 7, 11, 20, 23), (5, 9, 13, 16, 22)]The parameters of the design are:v = 25, r = 6, b1 = 6, k1 = 25, λ1 = 6, b2 = 30, k2 = 5, λ2 = 1Design 5: A resolvable NBIB design v = 49, k = 7
The corresponding parameters of the reduced form are obtained as follows: Let f = gcd(b, r, λ) = 1771, thenb1 = b/f = 53130/1771 = 30, r1 = r/f = 10626/1771 = 6, λ1 = λ /f = 1771/1771 = 1 [(6, 11, 16, 21, 1), (7, 12, 17, 22, 2), (8, 13, 18, 23, 3), (9, 14, 19, 24, 4), (10, 15, 20, 25, 5)][(6, 7, 8, 9, 10), (11, 12, 13, 14, 15), (16, 17, 18, 19, 20), (21, 22, 23, 24, 25), (1, 2, 3, 4, 5)][(1, 7, 13, 19, 25), (2, 10, 14, 16, 23), (3, 9, 12, 20, 21), (4, 6, 15, 18, 22), (5, 8, 11, 17, 24)][(1, 8, 14, 20, 22), (2, 9, 11, 18, 25), (3, 7, 15, 16, 24), (4, 10, 13, 17, 22), (5, 6, 12, 19, 23)][(1, 9, 15, 17, 23), (2, 6, 13, 20, 24), (3, 10, 11, 19, 22), (4, 8, 12, 16, 25), (5, 7, 14, 18, 21)][(1, 10, 12, 18, 24), (2, 8,15, 19, 21), (3, 6, 14, 17, 25), (4, 7, 11, 20, 23), (5, 9, 13, 16, 22)]The parameters of the design are:v = 25, r = 6, b1 = 6, k1 = 25, λ1 = 6, b2 = 30, k2 = 5, λ2 = 1Design 5: A resolvable NBIB design v = 49, k = 7 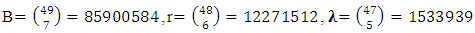 Let f = gcd(b, r, λ) = 1533939, then
Let f = gcd(b, r, λ) = 1533939, then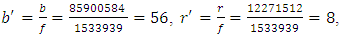
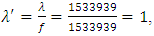 [(8, 15, 22, 29, 36, 43, 1), (9, 16, 23, 30, 37, 44, 2), (10. 17, 24, 31, 38, 45, 3), (11, 18, 25, 32, 39, 46, 4), (12, 19, 26, 33, 40, 47, 5), (13, 20, 27, 34, 41, 48, 6), (14, 21, 28, 35, 42, 49, 7)] [(8, 9, 10, 11, 12, 13, 14), (15, 16, 17, 18, 19, 20, 21), (22, 23, 24, 25, 26, 27, 28), (29, 30, 31, 32, 33, 34, 35), (36, 37, 38, 39, 40, 41, 42), (43, 44, 45, 46, 47, 48, 49), (1, 2, 3, 4, 5, 6, 7)][(8, 16, 24, 32, 40, 48, 7), (15, 23, 31, 39, 47, 6, 14), (22, 30, 38, 46, 5, 13, 21), (29, 37, 45, 4, 12, 20, 28), (36, 44, 3, 11, 19, 27, 35), (43, 2, 10, 18, 26, 34, 42), (1, 9, 17, 25, 33, 41, 49)][(8, 23, 38, 4, 19, 34, 49), (15, 30, 45, 11, 26, 41, 7), (22, 37, 3, 18, 33, 48, 14), (29, 44, 10, 25, 40, 6, 21), (36, 2, 17, 32, 47, 13, 28), (43, 9, 24, 39, 5, 20, 35), (1, 16, 31, 46, 12, 27, 42)][(8, 30, 3, 25, 47, 20, 42), (15, 37, 10, 32, 5, 27, 49), (22, 44, 17, 39, 12, 34, 7), (29, 2, 24, 46, 19, 41, 14), (36, 9, 31, 4, 26, 48, 21), (43, 16, 38, 11, 33, 6, 28), (1, 23, 45, 18, 40, 13, 35)][(8, 37, 17, 46, 26, 6, 35), (15, 44, 24, 4, 33, 13, 42), (22, 2, 31, 11, 40, 20, 49), (29, 9, 38, 18, 47, 27, 7), (36, 16, 45, 25, 5, 34, 14), (43, 23, 3, 32, 12, 41, 21), (1, 30, 10, 39, 19, 48, 28)][(8, 44, 31, 18, 5, 41, 28), (15, 2, 38, 25, 12, 48, 35), (22, 9, 45, 32, 19, 6, 42), (29, 16, 3, 39, 26, 13, 49), (36, 23, 10, 46, 33, 20, 7), (43, 30, 17, 4, 40, 27, 14), (1, 37, 24, 11, 47, 34, 21)][(8, 2, 45, 39, 33, 27, 21), (15, 9, 3, 46, 40, 34, 28), (22, 16, 10, 4, 47, 41, 35), (29, 23, 17, 11, 5, 48, 42), (36, 30, 24, 18, 12, 6, 49), (43, 37, 31, 25, 19, 13, 7), (1, 44, 38, 32, 26, 20, 14)]The parameters of the design are:v = 49, r = 8, b1 = 8, k1 = 49, λ1 = 8, b2 = 56, k2 = 7, λ2 = 1
[(8, 15, 22, 29, 36, 43, 1), (9, 16, 23, 30, 37, 44, 2), (10. 17, 24, 31, 38, 45, 3), (11, 18, 25, 32, 39, 46, 4), (12, 19, 26, 33, 40, 47, 5), (13, 20, 27, 34, 41, 48, 6), (14, 21, 28, 35, 42, 49, 7)] [(8, 9, 10, 11, 12, 13, 14), (15, 16, 17, 18, 19, 20, 21), (22, 23, 24, 25, 26, 27, 28), (29, 30, 31, 32, 33, 34, 35), (36, 37, 38, 39, 40, 41, 42), (43, 44, 45, 46, 47, 48, 49), (1, 2, 3, 4, 5, 6, 7)][(8, 16, 24, 32, 40, 48, 7), (15, 23, 31, 39, 47, 6, 14), (22, 30, 38, 46, 5, 13, 21), (29, 37, 45, 4, 12, 20, 28), (36, 44, 3, 11, 19, 27, 35), (43, 2, 10, 18, 26, 34, 42), (1, 9, 17, 25, 33, 41, 49)][(8, 23, 38, 4, 19, 34, 49), (15, 30, 45, 11, 26, 41, 7), (22, 37, 3, 18, 33, 48, 14), (29, 44, 10, 25, 40, 6, 21), (36, 2, 17, 32, 47, 13, 28), (43, 9, 24, 39, 5, 20, 35), (1, 16, 31, 46, 12, 27, 42)][(8, 30, 3, 25, 47, 20, 42), (15, 37, 10, 32, 5, 27, 49), (22, 44, 17, 39, 12, 34, 7), (29, 2, 24, 46, 19, 41, 14), (36, 9, 31, 4, 26, 48, 21), (43, 16, 38, 11, 33, 6, 28), (1, 23, 45, 18, 40, 13, 35)][(8, 37, 17, 46, 26, 6, 35), (15, 44, 24, 4, 33, 13, 42), (22, 2, 31, 11, 40, 20, 49), (29, 9, 38, 18, 47, 27, 7), (36, 16, 45, 25, 5, 34, 14), (43, 23, 3, 32, 12, 41, 21), (1, 30, 10, 39, 19, 48, 28)][(8, 44, 31, 18, 5, 41, 28), (15, 2, 38, 25, 12, 48, 35), (22, 9, 45, 32, 19, 6, 42), (29, 16, 3, 39, 26, 13, 49), (36, 23, 10, 46, 33, 20, 7), (43, 30, 17, 4, 40, 27, 14), (1, 37, 24, 11, 47, 34, 21)][(8, 2, 45, 39, 33, 27, 21), (15, 9, 3, 46, 40, 34, 28), (22, 16, 10, 4, 47, 41, 35), (29, 23, 17, 11, 5, 48, 42), (36, 30, 24, 18, 12, 6, 49), (43, 37, 31, 25, 19, 13, 7), (1, 44, 38, 32, 26, 20, 14)]The parameters of the design are:v = 49, r = 8, b1 = 8, k1 = 49, λ1 = 8, b2 = 56, k2 = 7, λ2 = 15. Conclusions
- From all the designs constructed in section 4, it is indeed clear that they are unique designs because of the fact that; fewer number of blocks are required, even when designs with large number of treatments that are interest. Also the parameters of the design for any given number of treatments are specified with ease prior to the construction of the full designs. For any nested balanced incomplete block designs to be referred to as coset-k2 resolvable, the design parameters are expected to satisfy the following relationship: v = k1 = k22, r = b1 = λ1, b2 = b1k1 = rk2 = λ1k2. The construction of designs when v is large requires tedious computational and combinatorial efforts.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML