-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2018; 8(4): 189-202
doi:10.5923/j.statistics.20180804.04

Biswas Members
Deapon Biswas
Transport Officer, Private Concern, Chittagong, Bangladesh
Correspondence to: Deapon Biswas, Transport Officer, Private Concern, Chittagong, Bangladesh.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

It covers all the sample points (B members) of a EB space, IB space (B event), CB space and GB space. EB space means elementary B space, IB space means identified B space, CB space means characterizing B space and GB space means general B space. EB space is nothing but the set of all sample points of the experiment “M sided N dice taken V at a time”. IB space is nothing but the set of sample points of the experiment “M sided N dice taken V at a time in which first v dice are identified in the first way or second way or both way”. CB space is nothing but the set of sample points of the experiment “M sided N dice taken V at a time in which vth dice characterized in the first way or second way or both way”. GB space is nothing but the set of sample points of the experiment “M sided N dice taken V at a time in which X is observed in the first way or Y is observed in the second way or X, Y are observed in the both way at a time”.
Keywords: EB experiment, EB related experiments, EB space, EB related spaces, IB experiment, IB related experiments, B event, B related events, CB experiment, CB related experiments, CB space, CB related spaces, GB experiment, GB related experiments, GB space and GB related spaces
Cite this paper: Deapon Biswas, Biswas Members, International Journal of Statistics and Applications, Vol. 8 No. 4, 2018, pp. 189-202. doi: 10.5923/j.statistics.20180804.04.
Article Outline
1. Introduction
- First of all elementary B spaces are divided into four parts; both way selected B (SB) space, both way arranged B (AB) space, first way selected and second way arranged B (SAB) space and first way arranged and second way selected B (ASB) space.Then identified B spaces or B events are divided into four parts i.e.,(i) both way selected B event (SB event)(ii) both way arranged B event (AB event)(iii) first way selected and second way arranged B event (SAB event )(iv) first way arranged and second way selected B event (ASB event). Similarly characterizing B spaces and general B spaces are divided into the same. To discuss the spaces first define respective experiments.
2. Findings
2.1. EB Experiment
- Definition 1.1 EB experiment: An EB experiment is an experiment that described the thing as the tossing of M sided N dice taken V at time. It is denoted by
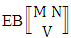 . (read EB experiment of M sided N dice taken V at a time). In terms of EB experiment we describe permutation and combination experiments as EB experiment of one sided N dice taken V at a time and homogenation and formation experiments as EB experiment of M sided V dice taken all at a time.Example 1.1: Denote the following experiments: (i) toss 3 sided 7 dice taken 4 at a time (ii) toss 6 sided 8 dice taken 5 at a time.Solution: The desired symbols are (i)
. (read EB experiment of M sided N dice taken V at a time). In terms of EB experiment we describe permutation and combination experiments as EB experiment of one sided N dice taken V at a time and homogenation and formation experiments as EB experiment of M sided V dice taken all at a time.Example 1.1: Denote the following experiments: (i) toss 3 sided 7 dice taken 4 at a time (ii) toss 6 sided 8 dice taken 5 at a time.Solution: The desired symbols are (i) 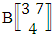 and
and 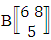 .Example 1.2: Denote the following experiments:(i) 7 balls taken 4 at a time where order is not taken into account(ii) 6 sided die tossed 4 times where order of the sides taken into account.Solution: The desired symbols are (i)
.Example 1.2: Denote the following experiments:(i) 7 balls taken 4 at a time where order is not taken into account(ii) 6 sided die tossed 4 times where order of the sides taken into account.Solution: The desired symbols are (i) 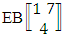 reads EB experiment of 1 sided 7 dice taken 4 at a time that remembers the experiment
reads EB experiment of 1 sided 7 dice taken 4 at a time that remembers the experiment 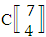 .(ii)
.(ii) 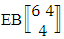 reads EB experiment of 6 sided 4 dice taken all at a time that remembers the experiment
reads EB experiment of 6 sided 4 dice taken all at a time that remembers the experiment 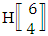 .
.2.2. EB Related Experiments
- The EB related experiments are ESB experiment, EAB experiment, ESAB experiment, EASB experiment.
2.3. EB Space
- Definition 1.2 EB space: An EB space is the set of all possible outcomes of the EB experiment
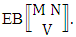 It is denoted by
It is denoted by 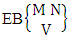 which reads EB space of M sided N dice taken V at a time. Now in terms of EB space we get permutation and combination spaces as EB space of one sided N dice taken V at a time and homogenation and formation spaces ass EB space of M sided V dice taken all at a time.Example 1.3: Find the B-space of 3 sided 4 dice taken 2 at a time.Solution: The desired EB space is
which reads EB space of M sided N dice taken V at a time. Now in terms of EB space we get permutation and combination spaces as EB space of one sided N dice taken V at a time and homogenation and formation spaces ass EB space of M sided V dice taken all at a time.Example 1.3: Find the B-space of 3 sided 4 dice taken 2 at a time.Solution: The desired EB space is 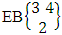 = {(b11 , b12 ), (b11 , b22 ), (b11 , b32 ), (b21 , b12 ), (b21 , b22 ), (b21 , b32 ), (b31 , b12 ), (b31 , b22 ), (b31 , b32 ), (b12 , b11 ), (b12 , b21 ), (b12 , b31 ), (b22 , b11 ), (b22 , b21 ), (b22 , b31 ), (b32 , b11 ), (b32 , b21 ), (b32 , b31 ), (b11 , b13 ), (b11 , b23 ), (b11 , b33 ), (b21 , b13 ), (b21 , b23 ), (b21 , b33 ), (b31 , b13 ), (b31 , b23 ), (b31 , b33 ), (b13 , b11 ), (b13 , b21 ), (b13 , b31 ), (b23 , b11 ), (b23 , b21 ), (b23 , b31 ), (b33 , b11 ), (b33 , b21 ), (b33 , b31 ), (b11 , b14 ), (b11 , b24 ), (b11 , b34 ), (b21 , b14 ), (b21 , b24 ), (b21 , b34 ), (b31 , b14 ), (b31 , b24 ), (b31 , b34 ), (b14 , b11 ), (b14 , b21 ), (b14 , b31 ), (b24 , b11 ), (b24 , b21 ), (b24 , b31 ), (b34 , b11 ), (b34 , b21 ), (b34 , b31 ), (b12 , b13 ), (b12 , b23 ), (b12 , b33 ), (b22 , b13 ), (b22 , b23 ), (b22 , b33 ), (b32 , b13 ), (b32 , b23 ), (b32 , b33 ), (b13 , b12 ), (b13 , b22 ), (b13 , b32 ), (b23 , b12 ), (b23 , b22 ), (b23 , b32 ), (b33 , b12 ), (b33 , b22 ), (b33 , b32 ), (b12 , b14 ), (b12 , b24 ), (b12 , b34 ), (b22 , b14 ), (b22 , b24 ), (b22 , b34 ), (b32 , b14 ), (b32 , b24 ), (b32 , b34 ), (b14 , b12 ), (b14 , b22 ), (b14 , b32 ), (b24 , b12 ), (b24 , b22 ), (b24 , b32 ), (b34 , b12 ), (b34 , b22 ), (b34 , b32 ), (b13 , b14 ), (b13 , b24 ), (b13 , b34 ), (b23 , b14), (b23 , b24 ), (b23 , b34 ), (b33 , b14 ), (b33 , b24 ), (b33 , b34 ), (b14 , b13), (b14 , b23 ), (b14 , b33 ), (b24 , b13 ), (b24 , b23 ), (b24 , b33 ), (b34 , b13), (b34 , b23 ), (b34 , b33 )}.Example 1.4: Find the EB space of the following experiments (i) draw 5 letters taken 2 at a time where order is taken into account (ii) toss 4 sided 3 dice where order of the sides of B members is not taken in to account.Solution: (i) The EB space of drawing 5 letters taken 2 at a time where order of the letters is taken into account is
= {(b11 , b12 ), (b11 , b22 ), (b11 , b32 ), (b21 , b12 ), (b21 , b22 ), (b21 , b32 ), (b31 , b12 ), (b31 , b22 ), (b31 , b32 ), (b12 , b11 ), (b12 , b21 ), (b12 , b31 ), (b22 , b11 ), (b22 , b21 ), (b22 , b31 ), (b32 , b11 ), (b32 , b21 ), (b32 , b31 ), (b11 , b13 ), (b11 , b23 ), (b11 , b33 ), (b21 , b13 ), (b21 , b23 ), (b21 , b33 ), (b31 , b13 ), (b31 , b23 ), (b31 , b33 ), (b13 , b11 ), (b13 , b21 ), (b13 , b31 ), (b23 , b11 ), (b23 , b21 ), (b23 , b31 ), (b33 , b11 ), (b33 , b21 ), (b33 , b31 ), (b11 , b14 ), (b11 , b24 ), (b11 , b34 ), (b21 , b14 ), (b21 , b24 ), (b21 , b34 ), (b31 , b14 ), (b31 , b24 ), (b31 , b34 ), (b14 , b11 ), (b14 , b21 ), (b14 , b31 ), (b24 , b11 ), (b24 , b21 ), (b24 , b31 ), (b34 , b11 ), (b34 , b21 ), (b34 , b31 ), (b12 , b13 ), (b12 , b23 ), (b12 , b33 ), (b22 , b13 ), (b22 , b23 ), (b22 , b33 ), (b32 , b13 ), (b32 , b23 ), (b32 , b33 ), (b13 , b12 ), (b13 , b22 ), (b13 , b32 ), (b23 , b12 ), (b23 , b22 ), (b23 , b32 ), (b33 , b12 ), (b33 , b22 ), (b33 , b32 ), (b12 , b14 ), (b12 , b24 ), (b12 , b34 ), (b22 , b14 ), (b22 , b24 ), (b22 , b34 ), (b32 , b14 ), (b32 , b24 ), (b32 , b34 ), (b14 , b12 ), (b14 , b22 ), (b14 , b32 ), (b24 , b12 ), (b24 , b22 ), (b24 , b32 ), (b34 , b12 ), (b34 , b22 ), (b34 , b32 ), (b13 , b14 ), (b13 , b24 ), (b13 , b34 ), (b23 , b14), (b23 , b24 ), (b23 , b34 ), (b33 , b14 ), (b33 , b24 ), (b33 , b34 ), (b14 , b13), (b14 , b23 ), (b14 , b33 ), (b24 , b13 ), (b24 , b23 ), (b24 , b33 ), (b34 , b13), (b34 , b23 ), (b34 , b33 )}.Example 1.4: Find the EB space of the following experiments (i) draw 5 letters taken 2 at a time where order is taken into account (ii) toss 4 sided 3 dice where order of the sides of B members is not taken in to account.Solution: (i) The EB space of drawing 5 letters taken 2 at a time where order of the letters is taken into account is 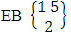 = {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b11 , b15 ), (b12 , b11 ), (b12 , b13 ), (b12 , b14 ), (b12 , b15 ), (b13 , b11 ), (b13 , b12 ), (b13 , b14 ), (b13 , b15 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b14 , b15 ), (b15 , b11 ), (b15 , b12 ), (b15 , b13 ), (b15 , b14 )}.The above EB space remembers you permutation space
= {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b11 , b15 ), (b12 , b11 ), (b12 , b13 ), (b12 , b14 ), (b12 , b15 ), (b13 , b11 ), (b13 , b12 ), (b13 , b14 ), (b13 , b15 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b14 , b15 ), (b15 , b11 ), (b15 , b12 ), (b15 , b13 ), (b15 , b14 )}.The above EB space remembers you permutation space 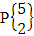 . In terms of EB space which reads EB space of one sided 5 dice taken 2 at a time.(ii) The EB space of tossing 4 sided 3 dice where order of the sides of B members is not taken into account is EB
. In terms of EB space which reads EB space of one sided 5 dice taken 2 at a time.(ii) The EB space of tossing 4 sided 3 dice where order of the sides of B members is not taken into account is EB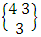 = {(b11 , b12 , b13 ), (b11 , b12 , b23 ), (b11 , b12 , b33 ), (b11 , b12 , b43 ), (b11 , b22 , b23 ), (b11 , b22 , b33 ), (b11 , b22 , b43 ), (b11 , b32 , b33), (b11 , b32 , b43 ), (b11 , b42 , b43 ), (b21 , b22 , b23 ), (b21 , b22, b33 ), (b21 , b22 , b43 ), (b21 , b32 , b33 ), (b21 , b32 , b43 ), (b21 , b42 , b43 ), (b31 , b32 , b33 ), (b31 , b32 , b43), (b31 , b42 , b43 ), (b41 , b42 , b43 )}.
= {(b11 , b12 , b13 ), (b11 , b12 , b23 ), (b11 , b12 , b33 ), (b11 , b12 , b43 ), (b11 , b22 , b23 ), (b11 , b22 , b33 ), (b11 , b22 , b43 ), (b11 , b32 , b33), (b11 , b32 , b43 ), (b11 , b42 , b43 ), (b21 , b22 , b23 ), (b21 , b22, b33 ), (b21 , b22 , b43 ), (b21 , b32 , b33 ), (b21 , b32 , b43 ), (b21 , b42 , b43 ), (b31 , b32 , b33 ), (b31 , b32 , b43), (b31 , b42 , b43 ), (b41 , b42 , b43 )}.2.4. EB Related Spaces
- Definition 1.3 ESB space: An ESB space is the set of all possible outcomes of the experiment
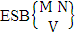 . In this case we found the components of B members are both way selected i.e., M way and N way selected. In other words order of the components of B members is not taken into account in the both way. It is denoted by
. In this case we found the components of B members are both way selected i.e., M way and N way selected. In other words order of the components of B members is not taken into account in the both way. It is denoted by 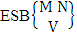 which reads ESB space of M sided N dice taken V at a time. Now in terms of ESB Space we get combination space
which reads ESB space of M sided N dice taken V at a time. Now in terms of ESB Space we get combination space 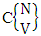 as the ESB space of one sided N dice taken V at a time and formation space
as the ESB space of one sided N dice taken V at a time and formation space 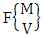 as the ESB space of M sided V dice taken all at a time. Example 1.5: Find the ESB space of 3 sided 5 dice taken 4 at a time.Solution: The desired ESB space is
as the ESB space of M sided V dice taken all at a time. Example 1.5: Find the ESB space of 3 sided 5 dice taken 4 at a time.Solution: The desired ESB space is 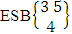 = {(b11 , b12 , b13 , b14 ), (b11, b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33 , b34 ), (b11, b22 , b23 , b24 ), (b11 , b22 , b23 , b34 ), (b11, b22 , b33 , b34 ), (b11 , b32 , b33 , b34 ), (b21, b22 , b23 , b24 ), (b21 , b22 , b23 , b34 ), (b21 , b22 , b33 , b34 ), (b21 , b32 , b33 , b34 ), (b31 , b32 , b33 , b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35 ), (b11 , b22 , b33 , b35 ), (b11 , b32 , b33 , b35 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b35 ), (b21 , b22 , b33 , b35 ), (b21 , b32 , b33 , b35 ), (b31 , b32 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 ), (b11 , b32 , b34 , b35 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b35 ), (b21 , b22 , b34 , b35 ), (b21 , b32 , b34 , b35 ), (b31 , b32 , b34 , b35 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b35 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b35 ), (b11 , b13 , b34 , b35 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b35 ), (b11 , b23 , b34 , b35 ), (b11 , b33 , b34 , b35 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b34 , b35 ), (b21 , b33 , b34 , b35 ), (b31 , b33 , b34 , b35 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b14 , b35 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b35 ), (b12 , b13 , b34 , b35 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b34 , b35 ), (b12 , b33 , b34 , b35 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b35 ), (b22 , b23 , b34 , b35 ), (b22 , b23 , b34 , b35 ), (b32 , b33 , b34 , b35 )}. Example 1.6: Find the ESB space of the following experiments (i) toss one sided 5 dice taken 4 at a time (ii) toss 3 sided 5 dice taken all at a time.Solution: (i) The desired ESB space of one sided 5 dice taken 4 at a time is
= {(b11 , b12 , b13 , b14 ), (b11, b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33 , b34 ), (b11, b22 , b23 , b24 ), (b11 , b22 , b23 , b34 ), (b11, b22 , b33 , b34 ), (b11 , b32 , b33 , b34 ), (b21, b22 , b23 , b24 ), (b21 , b22 , b23 , b34 ), (b21 , b22 , b33 , b34 ), (b21 , b32 , b33 , b34 ), (b31 , b32 , b33 , b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35 ), (b11 , b22 , b33 , b35 ), (b11 , b32 , b33 , b35 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b35 ), (b21 , b22 , b33 , b35 ), (b21 , b32 , b33 , b35 ), (b31 , b32 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 ), (b11 , b32 , b34 , b35 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b35 ), (b21 , b22 , b34 , b35 ), (b21 , b32 , b34 , b35 ), (b31 , b32 , b34 , b35 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b35 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b35 ), (b11 , b13 , b34 , b35 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b35 ), (b11 , b23 , b34 , b35 ), (b11 , b33 , b34 , b35 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b34 , b35 ), (b21 , b33 , b34 , b35 ), (b31 , b33 , b34 , b35 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b14 , b35 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b35 ), (b12 , b13 , b34 , b35 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b34 , b35 ), (b12 , b33 , b34 , b35 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b35 ), (b22 , b23 , b34 , b35 ), (b22 , b23 , b34 , b35 ), (b32 , b33 , b34 , b35 )}. Example 1.6: Find the ESB space of the following experiments (i) toss one sided 5 dice taken 4 at a time (ii) toss 3 sided 5 dice taken all at a time.Solution: (i) The desired ESB space of one sided 5 dice taken 4 at a time is 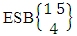 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12, b13 , b14, b15 )}.The ESB space remembers the combination space
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12, b13 , b14, b15 )}.The ESB space remembers the combination space 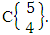 (ii) The desired ESB space of 3 sided 5 dice taken all at a time is
(ii) The desired ESB space of 3 sided 5 dice taken all at a time is 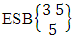 = {(b11 , b12 , b13 , b14 , b15 ), (b11 , b12 , b13 , b14 , b25 ), (b11 , b12 , b13 , b14 , b35 ), (b11 , b12 , b13 , b24 , b25 ), (b11 , b12 , b13 , b24 , b35 ), (b11 , b12 , b13 , b34 , b35 ), (b11 , b12 , b23 , b24 , b25 ), (b11 , b12 , b23 , b24 , b35 ), (b11 , b12 , b23 , b34 , b35 ), (b11 , b12 , b33 , b34 , b35 ), (b11 , b22 , b23 , b24 , b25 ), (b11 , b22 , b23 , b24 , b35 ), (b11 , b22 , b23 , b34 , b35 ), (b11 , b22 , b33 , b34 , b35 ), (b11 , b32 , b33 , b34 , b35 ), (b21 , b22 , b23 , b24 , b25 ), (b21 , b22 , b23 , b24 , b35 ), (b21 , b22 , b23 , b24 , b35 ), (b21 , b22 , b33 , b34 , b35 ), (b21 , b32 , b33 , b34 , b35 ), (b31 , b32 , b33 , b34 , b35 )}.The above SB space remembers the formation space
= {(b11 , b12 , b13 , b14 , b15 ), (b11 , b12 , b13 , b14 , b25 ), (b11 , b12 , b13 , b14 , b35 ), (b11 , b12 , b13 , b24 , b25 ), (b11 , b12 , b13 , b24 , b35 ), (b11 , b12 , b13 , b34 , b35 ), (b11 , b12 , b23 , b24 , b25 ), (b11 , b12 , b23 , b24 , b35 ), (b11 , b12 , b23 , b34 , b35 ), (b11 , b12 , b33 , b34 , b35 ), (b11 , b22 , b23 , b24 , b25 ), (b11 , b22 , b23 , b24 , b35 ), (b11 , b22 , b23 , b34 , b35 ), (b11 , b22 , b33 , b34 , b35 ), (b11 , b32 , b33 , b34 , b35 ), (b21 , b22 , b23 , b24 , b25 ), (b21 , b22 , b23 , b24 , b35 ), (b21 , b22 , b23 , b24 , b35 ), (b21 , b22 , b33 , b34 , b35 ), (b21 , b32 , b33 , b34 , b35 ), (b31 , b32 , b33 , b34 , b35 )}.The above SB space remembers the formation space 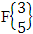 .Definition 1.4 EAB space: An EAB space is the set of all possible outcomes of the EAB experiment
.Definition 1.4 EAB space: An EAB space is the set of all possible outcomes of the EAB experiment 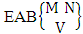 . In this case we found the components of B members are both way arranged i.e., M way and N way arranged. In other words order of the components of B members is taken into account in the both way. It is denoted by
. In this case we found the components of B members are both way arranged i.e., M way and N way arranged. In other words order of the components of B members is taken into account in the both way. It is denoted by 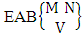 which reads EAB space of M sided N dice taken V at a time. Now in terms of EAB space we get permutation space as the EAB space of one sided N dice taken V at a time.Example 1.7: Find the EAB space of one sided 4 dice taken 2 at a time.Solution: The desired EAB space is
which reads EAB space of M sided N dice taken V at a time. Now in terms of EAB space we get permutation space as the EAB space of one sided N dice taken V at a time.Example 1.7: Find the EAB space of one sided 4 dice taken 2 at a time.Solution: The desired EAB space is 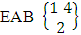 = {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b12 , b13 ), (b12 , b14 ), (b13 , b14 ), (b12 , b11 ), (b13 , b11 ), (b14 , b11 ), (b13 , b12 ), (b14 , b12 ), (b14 , b13 )}.The EAB space remembers the permutation space
= {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b12 , b13 ), (b12 , b14 ), (b13 , b14 ), (b12 , b11 ), (b13 , b11 ), (b14 , b11 ), (b13 , b12 ), (b14 , b12 ), (b14 , b13 )}.The EAB space remembers the permutation space 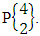 Definition 1.5 ESAB space: An ESAB space is the set of all possible outcomes of the experiment
Definition 1.5 ESAB space: An ESAB space is the set of all possible outcomes of the experiment 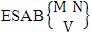 . In this case we found the components of B members of ESAB space are first way selected and second way arranged i.e., M way selected and N way arranged. In other words order of the components of B members of ESAB space is not taken into account in the first way and is taken into account in the second way. We denoted it as
. In this case we found the components of B members of ESAB space are first way selected and second way arranged i.e., M way selected and N way arranged. In other words order of the components of B members of ESAB space is not taken into account in the first way and is taken into account in the second way. We denoted it as 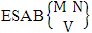 which reads ESAB space of M sided N dice taken V at a time. In terms of ESAB space we get permutation space
which reads ESAB space of M sided N dice taken V at a time. In terms of ESAB space we get permutation space 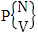 as the ESAB space of one sided N dice taken V at a time. Example 1.8: Find the ESAB space of one sided 5 dice taken 2 at a time.Solution: The desired ESAB space of one sided 5 dice taken 2 at a time is
as the ESAB space of one sided N dice taken V at a time. Example 1.8: Find the ESAB space of one sided 5 dice taken 2 at a time.Solution: The desired ESAB space of one sided 5 dice taken 2 at a time is 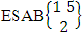 = {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b11 , b15 ), (b12 , b11 ), (b12 , b13 ), (b12 , b14 ), (b12 , b15 ), (b13 , b11 ), (b13 , b12 ), (b13 , b14 ), (b13 , b15 ), (b14 , b11 ), (b14 , b12), (b14 , b13 ), (b14 , b15 ), (b15 , b11 ), (b15 , b12 ), (b15 , b13 ), (b15 , b14 )}.The above space remembers us the permutation space
= {(b11 , b12 ), (b11 , b13 ), (b11 , b14 ), (b11 , b15 ), (b12 , b11 ), (b12 , b13 ), (b12 , b14 ), (b12 , b15 ), (b13 , b11 ), (b13 , b12 ), (b13 , b14 ), (b13 , b15 ), (b14 , b11 ), (b14 , b12), (b14 , b13 ), (b14 , b15 ), (b15 , b11 ), (b15 , b12 ), (b15 , b13 ), (b15 , b14 )}.The above space remembers us the permutation space 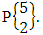 Definition 1.6 EASB space: An EASB space is the set of all possible outcomes of the experiment
Definition 1.6 EASB space: An EASB space is the set of all possible outcomes of the experiment 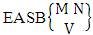 . In this case we found the components of B members are first way arranged and second way selected i.e., M way arranged and N way selected. In other words order of the components of B members is taken into account in the first way and is not taken into account in the second way. It is denoted by
. In this case we found the components of B members are first way arranged and second way selected i.e., M way arranged and N way selected. In other words order of the components of B members is taken into account in the first way and is not taken into account in the second way. It is denoted by 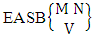 which reads EASB space of M sided N dice taken V at a time. Now in terms of EASB space we get combination space
which reads EASB space of M sided N dice taken V at a time. Now in terms of EASB space we get combination space 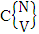 as the EASB space of one sided N dice taken V at a time and homogenation space
as the EASB space of one sided N dice taken V at a time and homogenation space 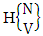 as the EASB space of M sided V dice taken all at a time.Example 1.9: Find the EASB space of 2 sided 5 dice taken 4 at a time.Solution: The desired EASB space of 2 sided 5 dice taken 4 at a time is
as the EASB space of M sided V dice taken all at a time.Example 1.9: Find the EASB space of 2 sided 5 dice taken 4 at a time.Solution: The desired EASB space of 2 sided 5 dice taken 4 at a time is 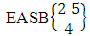 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b22 , b13 , b15 ), (b11 , b22 , b13 , b25 ), (b11 , b22 , b23 , b15 ), (b11 , b22 , b23 , b25 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b24 , b15 ), (b11 , b13 , b24 , b25 ),(b11 , b23 , b14 , b15 ), (b11 , b23 , b14 , b25 ), (b11 , b23 , b24 , b15 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b14 , b15 ), (b21 , b13, b14 , b25 ), (b21 , b13 , b24 , b15 ), (b21 , b13 , b24 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b24 , b25 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b24 , b25 ), (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b25 ), (b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 )}. Example 1.10: Find the EASB space of the following experiments (i) toss one sided 5 dice taken 4 at a time(ii) toss 2 sided 4 dice taken all at a time.Solution: (i) The desired EASB space is
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b22 , b13 , b15 ), (b11 , b22 , b13 , b25 ), (b11 , b22 , b23 , b15 ), (b11 , b22 , b23 , b25 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b24 , b15 ), (b11 , b13 , b24 , b25 ),(b11 , b23 , b14 , b15 ), (b11 , b23 , b14 , b25 ), (b11 , b23 , b24 , b15 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b14 , b15 ), (b21 , b13, b14 , b25 ), (b21 , b13 , b24 , b15 ), (b21 , b13 , b24 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b24 , b25 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b24 , b25 ), (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b25 ), (b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 )}. Example 1.10: Find the EASB space of the following experiments (i) toss one sided 5 dice taken 4 at a time(ii) toss 2 sided 4 dice taken all at a time.Solution: (i) The desired EASB space is 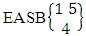 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12 , b13 , b14 , b15 )}.(ii) The desired EASB space is
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12 , b13 , b14 , b15 )}.(ii) The desired EASB space is 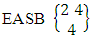 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23, b24 )}.
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23, b24 )}.2.5. IB Experiment
- Definition 1.7 IB experiment: An IB experiment is a B experiment that describes the things as the tossing of M sided N dice taken V at a time in which first v dice are identified in the first way or second way or both way. It is denoted by
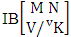 (read IB experiment of M sided N dice taken V at a time where first v dice identified).Example 1.11: Denote the IB experiment of tossing 6 sided 5 dice taken 4 at a time in which first 2 dice are identified.Solution: The desired symbol is
(read IB experiment of M sided N dice taken V at a time where first v dice identified).Example 1.11: Denote the IB experiment of tossing 6 sided 5 dice taken 4 at a time in which first 2 dice are identified.Solution: The desired symbol is 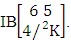
2.6. IB Related Experiments
- The IB related experiments are ISB experiment, IAB experiment, ISAB experiment, IASB experiment, first way IB experiment, second way IB experiment, both way IB experiment, first way ISB experiment, second way ISB experiment, both way ISB experiment, first way IAB experiment, second way IAB experiment, both way IAB experiment, first way IB experiment, second way IB experiment, both way IB experiment, first way ISAB experiment, second way ISAB experiment, both way ISAB experiment, first way IASB experiment, second way IASB experiment, both way IASB experiment,
2.7. B Event
- Definition 1.8 B event: It is a special kind of subset of a B space where the B members are to be have same first components, same second components, same third components and so on same vth components. In other words a B event is the set of all possible outcomes of the IB experiment
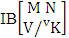 . Suppose the B members
. Suppose the B members 

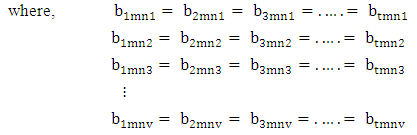 | (1.1) |
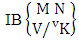 consists of
consists of  i.e.,
i.e.,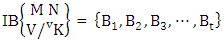 | (1.2) |
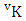 is a specified component assembly containing first v identified components.Example 1.12: Find the B events of the B space of example 1.9 where specified components assemblies are (i)
is a specified component assembly containing first v identified components.Example 1.12: Find the B events of the B space of example 1.9 where specified components assemblies are (i) 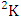 = (b11 , b12 ) and
= (b11 , b12 ) and 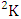 = (b21 , b22 ).Solution: The desired events are(i)
= (b21 , b22 ).Solution: The desired events are(i) 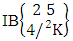 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), ( b11 , b12 , b24 , b25 )}. (ii)
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), ( b11 , b12 , b24 , b25 )}. (ii) 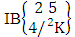 = {(b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ) , ( b21 , b22 , b24 , b25 )}.
= {(b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ) , ( b21 , b22 , b24 , b25 )}. 2.8. B Related Events
- Definition 1.9 SB event: A SB event is the set of all possible outcomes of the ISB experiment
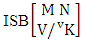 where
where 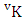 is a specified component assembly containing first v identified components. It is denoted by
is a specified component assembly containing first v identified components. It is denoted by 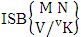 (read SB event of M sided N dice taken V at a time where first v components given).Example 1.13: Find the SB events of the SB space of example 1.5 where (i)
(read SB event of M sided N dice taken V at a time where first v components given).Example 1.13: Find the SB events of the SB space of example 1.5 where (i) 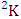 = (b11 , b12 ), (ii)
= (b11 , b12 ), (ii) 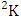 = (b11 , b22 ) and (iii)
= (b11 , b22 ) and (iii) 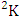 = (b21 , b32 ).Solution: The desired SB events are (i)
= (b21 , b32 ).Solution: The desired SB events are (i) 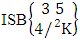 = {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33, b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35)}.(ii)
= {(b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33, b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35)}.(ii) 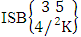 = {(b11 , b22 , b23 , b24), (b11 , b22 , b23 , b34), (b11 , b22 , b33 , b34 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35 ), (b11 , b22 , b33 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 )}.(iii)
= {(b11 , b22 , b23 , b24), (b11 , b22 , b23 , b34), (b11 , b22 , b33 , b34 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35 ), (b11 , b22 , b33 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 )}.(iii) 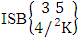 = {( b21 , b32 , b33 , b34 ), ( b21 , b32 , b33 , b35 ), ( b21 , b32 , b34 , b35 )}.Definition 1.10 AB event: An AB event is the set of all possible outcomes of the IAB experiment
= {( b21 , b32 , b33 , b34 ), ( b21 , b32 , b33 , b35 ), ( b21 , b32 , b34 , b35 )}.Definition 1.10 AB event: An AB event is the set of all possible outcomes of the IAB experiment 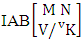 where
where 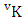 is a specified component assembly containing first v identified components. It is denoted by
is a specified component assembly containing first v identified components. It is denoted by 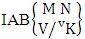 (read AB event of M sided N dice taken V at a time where first v components given).Example 1.14: Find the AB event of the IAB experiment
(read AB event of M sided N dice taken V at a time where first v components given).Example 1.14: Find the AB event of the IAB experiment 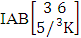 where
where 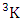 = (b21 , b22 , b13 ).Solution: The desired AB event is
= (b21 , b22 , b13 ).Solution: The desired AB event is 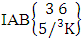 = (b21 , b22 , b13 , b14 , b15 ), (b21 , b22 , b13 , b14 , b16 ), (b21 , b22 , b13 , b15 , b14 ), (b21 , b22 , b13 , b15 , b16 ), (b21 , b22 , b13 , b16 , b14 ), (b21 , b22 , b13 , b16 , b15 ), (b21 , b22 , b13 , b14 , b25 ), (b21 , b22 , b13 , b14 , b26 ), (b21 , b22 , b13 , b15 , b24 ), (b21 , b22 , b13 , b15 , b26 ), (b21 , b22 , b13 , b16 , b24 ), (b21 , b22 , b13 , b16 , b25 ), (b21 , b22 , b13 , b14 , b35 ), (b21 , b22 , b13 , b14 , b36 ), (b21 , b22 , b13 , b15 , b34 ), (b21 , b22 , b13 , b15 , b36 ), (b21 , b22 , b13 , b16 , b34 ), (b21 , b22 , b13 , b16 , b35 ), (b21 , b22 , b13 , b24 , b15 ), (b21 , b22 , b13 , b24 , b16 ), (b21 , b22 , b13 , b25 , b14 ), (b21 , b22 , b13 , b25 , b16 ), (b21 , b22 , b13 , b26 , b14 ), (b21 , b22 , b13 , b26 , b15 ), (b21 , b22 , b13 , b24 , b25 ), (b21 , b22 , b13 , b24 , b26 ), (b21 , b22 , b13 , b25 , b24 ), (b21 , b22 , b13 , b25 , b26 ), (b21 , b22 , b13 , b26 , b24 ), (b21 , b22 , b13 , b26 , b25 ), (b21 , b22 , b13 , b24 , b35 ), (b21 , b22 , b13 , b24 , b36 ), (b21 , b22 , b13 , b25 , b34 ), (b21 , b22 , b13 , b25 , b36 ), (b21 , b22 , b13 , b26 , b34 ), (b21 , b22 , b13 , b26 , b35 ), (b21 , b22 , b13 , b34 , b15 ), (b21 , b22 , b13 , b34 , b16 ), (b21 , b22 , b13 , b35 , b14 ), (b21 , b22 , b13 , b35 , b16 ), (b21 , b22 , b13 , b36 , b14 ), (b21 , b22 , b13 , b36 , b15 ), (b21 , b22 , b13 , b34 , b25 ), (b21 , b22 , b13 , b34 , b26 ), (b21 , b22 , b13 , b35 , b24 ), (b21 , b22 , b13 , b35 , b26 ), (b21 , b22 , b13 , b36 , b24 ), (b21 , b22 , b13 , b36 , b25 ), (b21 , b22 , b13 , b34 , b35 ), (b21 , b22 , b13 , b34 , b36 ), (b21 , b22 , b13 , b35 , b34 ), (b21 , b22 , b13 , b35 , b36 ), (b21 , b22 , b13 , b36 , b34 ), (b21 , b22 , b13 , b36 , b35 ).Definition 1.11 SAB event: An SAB event is the set of all possible outcomes of the ISAB experiment
= (b21 , b22 , b13 , b14 , b15 ), (b21 , b22 , b13 , b14 , b16 ), (b21 , b22 , b13 , b15 , b14 ), (b21 , b22 , b13 , b15 , b16 ), (b21 , b22 , b13 , b16 , b14 ), (b21 , b22 , b13 , b16 , b15 ), (b21 , b22 , b13 , b14 , b25 ), (b21 , b22 , b13 , b14 , b26 ), (b21 , b22 , b13 , b15 , b24 ), (b21 , b22 , b13 , b15 , b26 ), (b21 , b22 , b13 , b16 , b24 ), (b21 , b22 , b13 , b16 , b25 ), (b21 , b22 , b13 , b14 , b35 ), (b21 , b22 , b13 , b14 , b36 ), (b21 , b22 , b13 , b15 , b34 ), (b21 , b22 , b13 , b15 , b36 ), (b21 , b22 , b13 , b16 , b34 ), (b21 , b22 , b13 , b16 , b35 ), (b21 , b22 , b13 , b24 , b15 ), (b21 , b22 , b13 , b24 , b16 ), (b21 , b22 , b13 , b25 , b14 ), (b21 , b22 , b13 , b25 , b16 ), (b21 , b22 , b13 , b26 , b14 ), (b21 , b22 , b13 , b26 , b15 ), (b21 , b22 , b13 , b24 , b25 ), (b21 , b22 , b13 , b24 , b26 ), (b21 , b22 , b13 , b25 , b24 ), (b21 , b22 , b13 , b25 , b26 ), (b21 , b22 , b13 , b26 , b24 ), (b21 , b22 , b13 , b26 , b25 ), (b21 , b22 , b13 , b24 , b35 ), (b21 , b22 , b13 , b24 , b36 ), (b21 , b22 , b13 , b25 , b34 ), (b21 , b22 , b13 , b25 , b36 ), (b21 , b22 , b13 , b26 , b34 ), (b21 , b22 , b13 , b26 , b35 ), (b21 , b22 , b13 , b34 , b15 ), (b21 , b22 , b13 , b34 , b16 ), (b21 , b22 , b13 , b35 , b14 ), (b21 , b22 , b13 , b35 , b16 ), (b21 , b22 , b13 , b36 , b14 ), (b21 , b22 , b13 , b36 , b15 ), (b21 , b22 , b13 , b34 , b25 ), (b21 , b22 , b13 , b34 , b26 ), (b21 , b22 , b13 , b35 , b24 ), (b21 , b22 , b13 , b35 , b26 ), (b21 , b22 , b13 , b36 , b24 ), (b21 , b22 , b13 , b36 , b25 ), (b21 , b22 , b13 , b34 , b35 ), (b21 , b22 , b13 , b34 , b36 ), (b21 , b22 , b13 , b35 , b34 ), (b21 , b22 , b13 , b35 , b36 ), (b21 , b22 , b13 , b36 , b34 ), (b21 , b22 , b13 , b36 , b35 ).Definition 1.11 SAB event: An SAB event is the set of all possible outcomes of the ISAB experiment 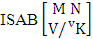 where
where 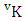 is a specified component assembly containing first v identified components. It is denoted by
is a specified component assembly containing first v identified components. It is denoted by 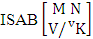 (read SAB event of M sided N dice taken V at a time where first v components given).Example 1.15: Find the SAB events of the ESAB space
(read SAB event of M sided N dice taken V at a time where first v components given).Example 1.15: Find the SAB events of the ESAB space 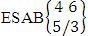 where (i)
where (i) 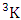 = (b11 , b13 , b22 ) and (ii)
= (b11 , b13 , b22 ) and (ii) 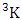 = (b23 , b34 , b31 ).Solution: The desired SAB events are (i)
= (b23 , b34 , b31 ).Solution: The desired SAB events are (i) 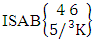 = {(b11 , b13 , b22 , b24 , b25 ), (b11 , b13 , b22 , b24 , b26 ), (b11 , b13 , b22 , b25 , b24), (b11 , b13 , b22 , b25 , b26 ), (b11 , b13 , b22 , b26 , b24 ), (b11 , b13 , b22 , b26 , b25 ), (b11 , b13 , b22 , b24 , b35 ), (b11 , b13 , b22 , b24 , b36 ), (b11 , b13 , b22 , b25 , b34 ), (b11 , b13 , b22 , b25 , b36 ), (b11 , b13 , b22 , b26 , b34 ), (b11 , b13 , b22 , b26 , b35 ), (b11 , b13 , b22 , b24 , b45 ), (b11 , b13 , b22 , b24 , b46 ), (b11 , b13 , b22 , b25 , b44 ), (b11 , b13 , b22 , b25 , b46 ), (b11 , b13 , b22 , b26 , b44 ), (b11 , b13 , b22 , b26 , b45 ),, (b11 , b13 , b22 , b34 , b35), (b11 , b13 , b22 , b34 , b36), (b11 , b13 , b22 , b35 , b34), (b11 , b13 , b22 , b35, b36 ), (b11 , b13 , b22 , b36 , b34 ), (b11 , b13 , b22 , b36 , b35 ), (b11 , b13 , b22 , b34 , b45 ), (b11 , b13 , b22 , b34 , b46 ), (b11 , b13 , b22 , b35 , b44 ), (b11 , b13 , b22 , b35 , b46 ), (b11 , b13 , b22 , b36 , b44), (b11 , b13 , b22 , b36 , b45 ), (b11 , b13 , b22 , b44 , b45 ), (b11 , b13 , b22 , b44 , b46 ), (b11 , b13 , b22 , b45 , b44 ), (b11 , b13 , b22 , b45 , b46), (b11 , b13 , b22 , b46 , b44 ), (b11 , b13 , b22 , b46 , b45)}.(ii)
= {(b11 , b13 , b22 , b24 , b25 ), (b11 , b13 , b22 , b24 , b26 ), (b11 , b13 , b22 , b25 , b24), (b11 , b13 , b22 , b25 , b26 ), (b11 , b13 , b22 , b26 , b24 ), (b11 , b13 , b22 , b26 , b25 ), (b11 , b13 , b22 , b24 , b35 ), (b11 , b13 , b22 , b24 , b36 ), (b11 , b13 , b22 , b25 , b34 ), (b11 , b13 , b22 , b25 , b36 ), (b11 , b13 , b22 , b26 , b34 ), (b11 , b13 , b22 , b26 , b35 ), (b11 , b13 , b22 , b24 , b45 ), (b11 , b13 , b22 , b24 , b46 ), (b11 , b13 , b22 , b25 , b44 ), (b11 , b13 , b22 , b25 , b46 ), (b11 , b13 , b22 , b26 , b44 ), (b11 , b13 , b22 , b26 , b45 ),, (b11 , b13 , b22 , b34 , b35), (b11 , b13 , b22 , b34 , b36), (b11 , b13 , b22 , b35 , b34), (b11 , b13 , b22 , b35, b36 ), (b11 , b13 , b22 , b36 , b34 ), (b11 , b13 , b22 , b36 , b35 ), (b11 , b13 , b22 , b34 , b45 ), (b11 , b13 , b22 , b34 , b46 ), (b11 , b13 , b22 , b35 , b44 ), (b11 , b13 , b22 , b35 , b46 ), (b11 , b13 , b22 , b36 , b44), (b11 , b13 , b22 , b36 , b45 ), (b11 , b13 , b22 , b44 , b45 ), (b11 , b13 , b22 , b44 , b46 ), (b11 , b13 , b22 , b45 , b44 ), (b11 , b13 , b22 , b45 , b46), (b11 , b13 , b22 , b46 , b44 ), (b11 , b13 , b22 , b46 , b45)}.(ii) 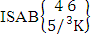 = {(b23 , b34 , b31 , b34 , b35 ), (b23 , b34 , b31 , b34 , b36), (b23 , b34 , b31 , b35 , b34), (b23 , b34 , b31 , b35 , b36 ), (b23 , b34 , b31 , b36 , b34 ), (b23 , b34 , b31 , b36 , b35 ), (b23 , b34 , b31 , b34 , b45 ), (b23 , b34 , b31 , b34 , b46 ), (b23 , b34 , b31 , b35 , b44 ), (b23 , b34 , b31 , b35 , b46 ), (b23 , b34 , b31 , b36 , b44 ), (b23 , b34 , b31 , b36 , b45 ), (b23 , b34 , b31 , b44 , b45 ), (b23 , b34 , b31 , b44 , b46 ), (b23 , b34 , b31 , b45 , b44 ), (b23 , b34 , b31 , b45 , b46 ), (b23 , b34 , b31 , b46 , b44), (b23 , b34 , b31 , b46 , b45)}.Definition 1.12 ASB event: An ASB event is the set of all possible outcomes of the IASB experiment
= {(b23 , b34 , b31 , b34 , b35 ), (b23 , b34 , b31 , b34 , b36), (b23 , b34 , b31 , b35 , b34), (b23 , b34 , b31 , b35 , b36 ), (b23 , b34 , b31 , b36 , b34 ), (b23 , b34 , b31 , b36 , b35 ), (b23 , b34 , b31 , b34 , b45 ), (b23 , b34 , b31 , b34 , b46 ), (b23 , b34 , b31 , b35 , b44 ), (b23 , b34 , b31 , b35 , b46 ), (b23 , b34 , b31 , b36 , b44 ), (b23 , b34 , b31 , b36 , b45 ), (b23 , b34 , b31 , b44 , b45 ), (b23 , b34 , b31 , b44 , b46 ), (b23 , b34 , b31 , b45 , b44 ), (b23 , b34 , b31 , b45 , b46 ), (b23 , b34 , b31 , b46 , b44), (b23 , b34 , b31 , b46 , b45)}.Definition 1.12 ASB event: An ASB event is the set of all possible outcomes of the IASB experiment 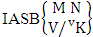 where
where 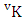 is a specified component assembly containing first v identified components. It is denoted by
is a specified component assembly containing first v identified components. It is denoted by 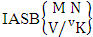 (read ASB event of M sided N dice taken V at a time where first v components given).Example 1.16: Find the ASB events of the EASB space of example 1.3 where (i)
(read ASB event of M sided N dice taken V at a time where first v components given).Example 1.16: Find the ASB events of the EASB space of example 1.3 where (i) 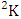 = (b21 , b12 ), (ii)
= (b21 , b12 ), (ii) 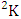 = (b21 , b23 ) and (iii)
= (b21 , b23 ) and (iii) 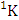 = (b22 )Solution: The desired ASB events are (i)
= (b22 )Solution: The desired ASB events are (i) 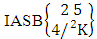 = {(b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 )}. (ii)
= {(b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 )}. (ii) 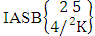 = {(b21 , b23 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b24 , b25 )}. (ii)
= {(b21 , b23 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), (b21 , b23 , b24 , b25 )}. (ii) 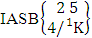 = {(b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 )}. We now describe three kinds of B events i.e., first way B event or first way IB space, second way B event or second way IB space and both way B event or both way IB space and their different forms.Definition 1.13 First way B event: A first way B event is the set of all possible outcomes of the first way IB experiment
= {(b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 )}. We now describe three kinds of B events i.e., first way B event or first way IB space, second way B event or second way IB space and both way B event or both way IB space and their different forms.Definition 1.13 First way B event: A first way B event is the set of all possible outcomes of the first way IB experiment 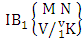 where first v identified m’s are given and n’s are not given. It is denoted by
where first v identified m’s are given and n’s are not given. It is denoted by 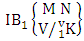 (read first way B event of M sided N dice taken V at a time where first v identified m’s are given).Example 1.17: Find the first way B event against the first way IB experiment
(read first way B event of M sided N dice taken V at a time where first v identified m’s are given).Example 1.17: Find the first way B event against the first way IB experiment 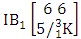 where first 3 identified m’s are 2, 3 and 4.Solution: The desired first way B event is
where first 3 identified m’s are 2, 3 and 4.Solution: The desired first way B event is 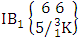 = (b21 , b32 , b43 , b44 , b45 ), (b21 , b32 , b43 , b44 , b55 ), (b21 , b32 , b43 , b44 , b65 ), (b21 , b32 , b43 , b54 , b55 ), (b21 , b32 , b43 , b54 , b65 ), (b21 , b32 , b43 , b64 , b65 ), (b21 , b32 , b43 , b44 , b46 ), (b21 , b32 , b43 , b44 , b56 ), (b21 , b32 , b43 , b44 , b66 ), (b21 , b32 , b43 , b54 , b56 ), (b21 , b32 , b43 , b54 , b66 ), (b21 , b32 , b43 , b64 , b66 ), (b21 , b32 , b43 , b45 , b46 ), (b21 , b32 , b43 , b45 , b56 ), (b21 , b32 , b43 , b45 , b66 ), (b21 , b32 , b43 , b55 , b56 ), (b21 , b32 , b43 , b55 , b66 ), (b21 , b32 , b43 , b65 , b66 ), (b21 , b32 , b44 , b45 , b46 ), (b21 , b32 , b44 , b45 , b56 ), (b21 , b32 , b44 , b45 , b66 ), (b21 , b32 , b44 , b55 , b56 ), (b21 , b32 , b44 , b55 , b66 ), (b21 , b32 , b44 , b65 , b66 ), (b21 , b33 , b44 , b45 , b46 ), (b21 , b33 , b44 , b45 , b56 ), (b21 , b33 , b44 , b45 , b66 ), (b21 , b33 , b44 , b55 , b56 ), (b21 , b33 , b44 , b55 , b66 ), (b21 , b33 , b44 , b65 , b66 ), (b22 , b33 , b44 , b45 , b46 ), (b22 , b33 , b44 , b45 , b56 ), (b22 , b33 , b44 , b45 , b66 ), (b22 , b33 , b44 , b55 , b56 ), (b22 , b33 , b44 , b55 , b66 ), (b22 , b33 , b44 , b65 , b66 ).Definition 1.14 Second way B event: A second way B event is the set of all possible outcomes of the second way IB experiment
= (b21 , b32 , b43 , b44 , b45 ), (b21 , b32 , b43 , b44 , b55 ), (b21 , b32 , b43 , b44 , b65 ), (b21 , b32 , b43 , b54 , b55 ), (b21 , b32 , b43 , b54 , b65 ), (b21 , b32 , b43 , b64 , b65 ), (b21 , b32 , b43 , b44 , b46 ), (b21 , b32 , b43 , b44 , b56 ), (b21 , b32 , b43 , b44 , b66 ), (b21 , b32 , b43 , b54 , b56 ), (b21 , b32 , b43 , b54 , b66 ), (b21 , b32 , b43 , b64 , b66 ), (b21 , b32 , b43 , b45 , b46 ), (b21 , b32 , b43 , b45 , b56 ), (b21 , b32 , b43 , b45 , b66 ), (b21 , b32 , b43 , b55 , b56 ), (b21 , b32 , b43 , b55 , b66 ), (b21 , b32 , b43 , b65 , b66 ), (b21 , b32 , b44 , b45 , b46 ), (b21 , b32 , b44 , b45 , b56 ), (b21 , b32 , b44 , b45 , b66 ), (b21 , b32 , b44 , b55 , b56 ), (b21 , b32 , b44 , b55 , b66 ), (b21 , b32 , b44 , b65 , b66 ), (b21 , b33 , b44 , b45 , b46 ), (b21 , b33 , b44 , b45 , b56 ), (b21 , b33 , b44 , b45 , b66 ), (b21 , b33 , b44 , b55 , b56 ), (b21 , b33 , b44 , b55 , b66 ), (b21 , b33 , b44 , b65 , b66 ), (b22 , b33 , b44 , b45 , b46 ), (b22 , b33 , b44 , b45 , b56 ), (b22 , b33 , b44 , b45 , b66 ), (b22 , b33 , b44 , b55 , b56 ), (b22 , b33 , b44 , b55 , b66 ), (b22 , b33 , b44 , b65 , b66 ).Definition 1.14 Second way B event: A second way B event is the set of all possible outcomes of the second way IB experiment 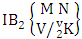 where first v identified n’s are given and m’s are not given. It is denoted by
where first v identified n’s are given and m’s are not given. It is denoted by 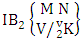 (read second way B event of M sided N dice taken V at a time where first v identified n’s are given).Example 1.18: Find the second way B event against the second way IB experiment
(read second way B event of M sided N dice taken V at a time where first v identified n’s are given).Example 1.18: Find the second way B event against the second way IB experiment 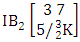 where first 3 identified n’s are 1, 3 and 5.Solution: The desired second way B event is
where first 3 identified n’s are 1, 3 and 5.Solution: The desired second way B event is 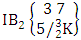 = (b11 , b13 , b15 , b16 , b17 ), (b11 , b13 , b15 , b16 , b27 ), (b11 , b13 , b15 , b16 , b37 ), (b11 , b13 , b15 , b26 , b27 ), (b11 , b13 , b15 , b26 , b37), (b11 , b13 , b15 , b36 , b37 ), (b11 , b13 , b25 , b26 , b27 ), (b11 , b13 , b25 , b26 , b37 ), (b11 , b13 , b25 , b36 , b37 ), (b11 , b13 , b35 , b36 , b37 ), (b11 , b23 , b25 , b26 , b27 ), (b11 , b23 , b25 , b26 , b37 ), (b11 , b23 , b25 , b36 , b37 ), (b11 , b23 , b35 , b36 , b37 ), (b11 , b33 , b35 , b36 , b37), (b21 , b23 , b25 , b26 , b27 ), (b11 , b23 , b25 , b26 , b37 ), (b21 , b23 , b25 , b36 , b37 ), (b21 , b23 , b35 , b36 , b37 ), (b21 , b33 , b35 , b36 , b37 ), (b31 , b33 , b35 , b36 , b37 ).Definition 1.15 Both way B event: A both way B event is the set of all possible outcomes of the both way IB experiment
= (b11 , b13 , b15 , b16 , b17 ), (b11 , b13 , b15 , b16 , b27 ), (b11 , b13 , b15 , b16 , b37 ), (b11 , b13 , b15 , b26 , b27 ), (b11 , b13 , b15 , b26 , b37), (b11 , b13 , b15 , b36 , b37 ), (b11 , b13 , b25 , b26 , b27 ), (b11 , b13 , b25 , b26 , b37 ), (b11 , b13 , b25 , b36 , b37 ), (b11 , b13 , b35 , b36 , b37 ), (b11 , b23 , b25 , b26 , b27 ), (b11 , b23 , b25 , b26 , b37 ), (b11 , b23 , b25 , b36 , b37 ), (b11 , b23 , b35 , b36 , b37 ), (b11 , b33 , b35 , b36 , b37), (b21 , b23 , b25 , b26 , b27 ), (b11 , b23 , b25 , b26 , b37 ), (b21 , b23 , b25 , b36 , b37 ), (b21 , b23 , b35 , b36 , b37 ), (b21 , b33 , b35 , b36 , b37 ), (b31 , b33 , b35 , b36 , b37 ).Definition 1.15 Both way B event: A both way B event is the set of all possible outcomes of the both way IB experiment 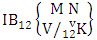 where first v identified m’s and n’s are given. It is denoted by
where first v identified m’s and n’s are given. It is denoted by 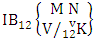 (read both way B event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.19: Find the both way B event against the both way IB experiment
(read both way B event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.19: Find the both way B event against the both way IB experiment 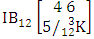 where first m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: The desired both way B event is
where first m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: The desired both way B event is 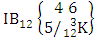 = (b12 , b23 , b24 , b21 , b25 ), (b12 , b23 , b24 , b21 , b26 ), (b12 , b23 , b24 , b25 , b21 ), (b12 , b23 , b24 , b25 , b26 ), (b12 , b23 , b24 , b26 , b21 ), (b12 , b23 , b24 , b26 , b25 ), (b12 , b23 , b24 , b21 , b35 ), (b12 , b23 , b24 , b21 , b36 ), (b12 , b23 , b24 , b25 , b31 ), (b12 , b23 , b24 , b25 , b36 ) , (b12 , b23 , b24 , b26 , b31 ), (b12 , b23 , b24 , b26 , b35 ), (b12 , b23 , b24 , b21 , b45 ), (b12 , b23 , b24 , b21 , b46 ), (b12 , b23 , b24 , b25 , b41 ), (b12 , b23 , b24 , b25 , b46 ), (b12 , b23 , b24 , b26 , b41 ), (b12 , b23 , b24 , b26 , b45 ), (b12 , b23 , b24 , b31 , b35 ), (b12 , b23 , b24 , b31 , b36 ), (b12 , b23 , b24 , b35 , b31 ), (b12 , b23 , b24 , b35 , b36 ), (b12 , b23 , b24 , b36 , b31 ), (b12 , b23 , b24 , b36 , b35 ), (b12 , b23 , b24 , b31 , b45 ), (b12 , b23 , b24 , b31 , b46 ), (b12 , b23 , b24 , b35 , b41 ), (b12 , b23 , b24 , b35 , b46 ), (b12 , b23 , b24 , b36 , b41 ), (b12 , b23 , b24 , b36 , b45 ), (b12 , b23 , b24 , b41 , b45 ), (b12 , b23 , b24 , b41 , b46 ), (b12 , b23 , b24 , b45 , b41 ), (b12 , b23 , b24 , b45 , b46 ), (b12 , b23 , b24 , b46 , b41 ), (b12 , b23 , b24 , b46 , b45 ).Definition 1.16 First way SB event: A first way SB event is the set of all possible outcomes of the first way ISB experiment
= (b12 , b23 , b24 , b21 , b25 ), (b12 , b23 , b24 , b21 , b26 ), (b12 , b23 , b24 , b25 , b21 ), (b12 , b23 , b24 , b25 , b26 ), (b12 , b23 , b24 , b26 , b21 ), (b12 , b23 , b24 , b26 , b25 ), (b12 , b23 , b24 , b21 , b35 ), (b12 , b23 , b24 , b21 , b36 ), (b12 , b23 , b24 , b25 , b31 ), (b12 , b23 , b24 , b25 , b36 ) , (b12 , b23 , b24 , b26 , b31 ), (b12 , b23 , b24 , b26 , b35 ), (b12 , b23 , b24 , b21 , b45 ), (b12 , b23 , b24 , b21 , b46 ), (b12 , b23 , b24 , b25 , b41 ), (b12 , b23 , b24 , b25 , b46 ), (b12 , b23 , b24 , b26 , b41 ), (b12 , b23 , b24 , b26 , b45 ), (b12 , b23 , b24 , b31 , b35 ), (b12 , b23 , b24 , b31 , b36 ), (b12 , b23 , b24 , b35 , b31 ), (b12 , b23 , b24 , b35 , b36 ), (b12 , b23 , b24 , b36 , b31 ), (b12 , b23 , b24 , b36 , b35 ), (b12 , b23 , b24 , b31 , b45 ), (b12 , b23 , b24 , b31 , b46 ), (b12 , b23 , b24 , b35 , b41 ), (b12 , b23 , b24 , b35 , b46 ), (b12 , b23 , b24 , b36 , b41 ), (b12 , b23 , b24 , b36 , b45 ), (b12 , b23 , b24 , b41 , b45 ), (b12 , b23 , b24 , b41 , b46 ), (b12 , b23 , b24 , b45 , b41 ), (b12 , b23 , b24 , b45 , b46 ), (b12 , b23 , b24 , b46 , b41 ), (b12 , b23 , b24 , b46 , b45 ).Definition 1.16 First way SB event: A first way SB event is the set of all possible outcomes of the first way ISB experiment 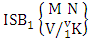 where first v identified m’s are given and n’s are not given. It is denoted by
where first v identified m’s are given and n’s are not given. It is denoted by 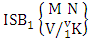 (read first way SB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.17 Second way SB event: A second way SB event is the set of all possible outcomes of the second way ISB experiment
(read first way SB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.17 Second way SB event: A second way SB event is the set of all possible outcomes of the second way ISB experiment 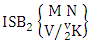 where first v identified n’s are given and m’s are not given. It is denoted by
where first v identified n’s are given and m’s are not given. It is denoted by 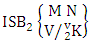 (read second way SB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.18 Both way SB event: A both way SB event is the set of all possible outcomes of the both way ISB experiment
(read second way SB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.18 Both way SB event: A both way SB event is the set of all possible outcomes of the both way ISB experiment 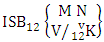 where first v identified m’s and n’s are given. It is denoted by
where first v identified m’s and n’s are given. It is denoted by 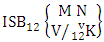 (read both way SB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.20: Find the both way SB event against the both way ISB experiment
(read both way SB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.20: Find the both way SB event against the both way ISB experiment 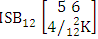 where first m’s are 2, 2 and n’s are 1, 3.Solution: The desired both way SB event is
where first m’s are 2, 2 and n’s are 1, 3.Solution: The desired both way SB event is 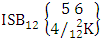 = (b21 , b23 , b24 , b25 ) , (b21 , b23 , b24 , b26 ), (b21 , b23 , b25 , b26 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b24 , b36 ), (b21 , b23 , b25 , b36 ), (b21 , b23 , b24 , b45 ), (b21 , b23 , b24 , b46 ), (b21 , b23 , b25 , b46 ) , (b21 , b23 , b24 , b55 ), (b21 , b23 , b24 , b56 ), (b21 , b23 , b25 , b56 ), (b21 , b23 , b34 , b35 ), (b21 , b23 , b34 , b36 ), (b21 , b23 , b35 , b36 ), (b21 , b23 , b34 , b45 ), (b21 , b23 , b34 , b46 ) , (b21 , b23 , b35 , b46 ), (b21 , b23 , b34 , b55 ), (b21 , b23 , b34 , b56 ), (b21 , b23 , b35 , b56 ), (b21 , b23 , b44 , b45 ), (b21 , b23 , b44 , b46 ), (b21 , b23 , b45 , b46 ), (b21 , b23 , b44 , b55 ), (b21 , b23 , b44 , b56 ), (b21 , b23 , b45 , b56 ), (b21 , b23 , b54 , b55 ), (b21 , b23 , b54 , b56 ), (b21 , b23 , b55 , b56 ).Definition 1.19 First way AB event: A first way AB event is the set of all possible outcomes of the first way IAB experiment
= (b21 , b23 , b24 , b25 ) , (b21 , b23 , b24 , b26 ), (b21 , b23 , b25 , b26 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b24 , b36 ), (b21 , b23 , b25 , b36 ), (b21 , b23 , b24 , b45 ), (b21 , b23 , b24 , b46 ), (b21 , b23 , b25 , b46 ) , (b21 , b23 , b24 , b55 ), (b21 , b23 , b24 , b56 ), (b21 , b23 , b25 , b56 ), (b21 , b23 , b34 , b35 ), (b21 , b23 , b34 , b36 ), (b21 , b23 , b35 , b36 ), (b21 , b23 , b34 , b45 ), (b21 , b23 , b34 , b46 ) , (b21 , b23 , b35 , b46 ), (b21 , b23 , b34 , b55 ), (b21 , b23 , b34 , b56 ), (b21 , b23 , b35 , b56 ), (b21 , b23 , b44 , b45 ), (b21 , b23 , b44 , b46 ), (b21 , b23 , b45 , b46 ), (b21 , b23 , b44 , b55 ), (b21 , b23 , b44 , b56 ), (b21 , b23 , b45 , b56 ), (b21 , b23 , b54 , b55 ), (b21 , b23 , b54 , b56 ), (b21 , b23 , b55 , b56 ).Definition 1.19 First way AB event: A first way AB event is the set of all possible outcomes of the first way IAB experiment 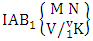 where first v identified m’s are given and n’s are not given. It is denoted by
where first v identified m’s are given and n’s are not given. It is denoted by 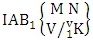 (read first way AB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.20 Second way AB event: A second way AB event is the set of all possible outcomes of the second way IAB experiment
(read first way AB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.20 Second way AB event: A second way AB event is the set of all possible outcomes of the second way IAB experiment 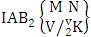 where first v identified n’s are given and m’s are not given. It is denoted by
where first v identified n’s are given and m’s are not given. It is denoted by 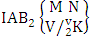 (read second way AB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.21 Both way AB event: A both way AB event is the set of all possible outcomes of the both way IAB experiment
(read second way AB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.21 Both way AB event: A both way AB event is the set of all possible outcomes of the both way IAB experiment 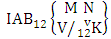 where first v identified m’s and n’s are given. It is denoted by
where first v identified m’s and n’s are given. It is denoted by 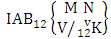 (read both way AB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.21: Find the both way AB event against the both way IAB experiment
(read both way AB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.21: Find the both way AB event against the both way IAB experiment 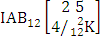 where first m’s are 1, 1 and n’s are 2, 3.Solution: The desired both way AB event is
where first m’s are 1, 1 and n’s are 2, 3.Solution: The desired both way AB event is 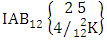 = (b12 , b13 , b11 , b14 ), (b12 , b13 , b11 , b15 ), (b12 , b13 , b14 , b11 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b15 , b11 ), (b12 , b13 , b15 , b14 ), (b12 , b13 , b11 , b24 ), (b12 , b13 , b11 , b25 ), (b12 , b13 , b14 , b21 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b15 , b21 ), (b12 , b13 , b15 , b24 ), (b12 , b13 , b21 , b14 ), (b12 , b13 , b21 , b15 ), (b12 , b13 , b24 , b11 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b25 , b11 ), (b12 , b13 , b25 , b14 ), (b12 , b13 , b21 , b24 ), (b12 , b13 , b21 , b25 ), (b12 , b13 , b24 , b21 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b25 , b21 ), (b12 , b13 , b25 , b24 ). Definition 1.22 First way SAB event: A first way SAB event is the set of all possible outcomes of the first way ISAB experiment
= (b12 , b13 , b11 , b14 ), (b12 , b13 , b11 , b15 ), (b12 , b13 , b14 , b11 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b15 , b11 ), (b12 , b13 , b15 , b14 ), (b12 , b13 , b11 , b24 ), (b12 , b13 , b11 , b25 ), (b12 , b13 , b14 , b21 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b15 , b21 ), (b12 , b13 , b15 , b24 ), (b12 , b13 , b21 , b14 ), (b12 , b13 , b21 , b15 ), (b12 , b13 , b24 , b11 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b25 , b11 ), (b12 , b13 , b25 , b14 ), (b12 , b13 , b21 , b24 ), (b12 , b13 , b21 , b25 ), (b12 , b13 , b24 , b21 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b25 , b21 ), (b12 , b13 , b25 , b24 ). Definition 1.22 First way SAB event: A first way SAB event is the set of all possible outcomes of the first way ISAB experiment 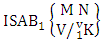 where first v identified m’s are given and n’s are not given. It is denoted by
where first v identified m’s are given and n’s are not given. It is denoted by 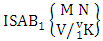 (read first way SAB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.23 Second way SAB event: A second way SAB event is the set of all possible outcomes of the second way ISAB experiment
(read first way SAB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.23 Second way SAB event: A second way SAB event is the set of all possible outcomes of the second way ISAB experiment 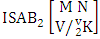 where first v identified m’s are given and m’s are not given. It is denoted by
where first v identified m’s are given and m’s are not given. It is denoted by 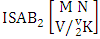 (read second way SAB event of M sided N dice taken V at a time where first v identified n’s are given ).Definition 1.24 Both way SAB event: A both way SAB event is the set of all possible outcomes of the both way ISAB experiment
(read second way SAB event of M sided N dice taken V at a time where first v identified n’s are given ).Definition 1.24 Both way SAB event: A both way SAB event is the set of all possible outcomes of the both way ISAB experiment 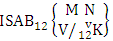 where first v identified m’s and n’s are given. It is denoted by
where first v identified m’s and n’s are given. It is denoted by 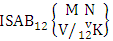 (read both way SAB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.22: Find the both way SAB event against the both way ISAB experiment
(read both way SAB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.22: Find the both way SAB event against the both way ISAB experiment 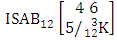 where first m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: The solution is the same as the solution of example 1.3.19.Definition 1.25 First way ASB event: A first way ASB event is the set of all possible outcomes of the first way IASB experiment
where first m’s are 1, 2, 2 and n’s are 2, 3, 4.Solution: The solution is the same as the solution of example 1.3.19.Definition 1.25 First way ASB event: A first way ASB event is the set of all possible outcomes of the first way IASB experiment 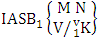 where first v identified m’s are given and n’s are not given. It is denoted by
where first v identified m’s are given and n’s are not given. It is denoted by 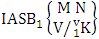 (read first way ASB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.26 Second way ASB event: A second way ASB event is the set of all possible outcomes of the second way IASB experiment
(read first way ASB event of M sided N dice taken V at a time where first v identified m’s are given).Definition 1.26 Second way ASB event: A second way ASB event is the set of all possible outcomes of the second way IASB experiment 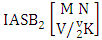 where first v identified n’s are given and m’s are not given. It is denoted by
where first v identified n’s are given and m’s are not given. It is denoted by 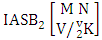 (read second way ASB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.27 Both way ASB event: A both way ASB event is the set of all possible outcomes of the both way IASB experiment
(read second way ASB event of M sided N dice taken V at a time where first v identified n’s are given).Definition 1.27 Both way ASB event: A both way ASB event is the set of all possible outcomes of the both way IASB experiment 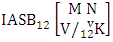 where first v identified m’s and n’s are given. It is denoted by
where first v identified m’s and n’s are given. It is denoted by 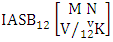 (read both way ASB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.23: Find the both way ASB event against the both IASB experiment
(read both way ASB event of M sided N dice taken V at a time where first v identified m’s and n’s are given).Example 1.23: Find the both way ASB event against the both IASB experiment 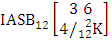 where first m’s are 1, 2 and n’s are 2, 3.Solution: The desired both way ASB event is
where first m’s are 1, 2 and n’s are 2, 3.Solution: The desired both way ASB event is 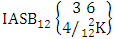 = (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b16 ), (b12 , b23 , b15 , b16 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b14 , b26 ), (b12 , b23 , b15 , b26 ), (b12 , b23 , b14 , b35 ), (b12 , b23 , b14 , b36 ), (b12 , b23 , b15 , b36 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b16 ), (b12 , b23 , b25 , b16 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b26 ), (b12 , b23 , b25 , b26 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b24 , b36 ), (b12 , b23 , b25 , b36 ), (b12 , b23 , b34 , b15 ), (b12 , b23 , b34 , b16 ), (b12 , b23 , b35 , b16 ), (b12 , b23 , b34 , b25 ), (b12 , b23 , b34 , b26 ), (b12 , b23 , b35 , b26 ), (b12 , b23 , b34 , b35 ), (b12 , b23 , b34 , b36 ), (b12 , b23 , b35 , b36 ).
= (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b16 ), (b12 , b23 , b15 , b16 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b14 , b26 ), (b12 , b23 , b15 , b26 ), (b12 , b23 , b14 , b35 ), (b12 , b23 , b14 , b36 ), (b12 , b23 , b15 , b36 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b16 ), (b12 , b23 , b25 , b16 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b26 ), (b12 , b23 , b25 , b26 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b24 , b36 ), (b12 , b23 , b25 , b36 ), (b12 , b23 , b34 , b15 ), (b12 , b23 , b34 , b16 ), (b12 , b23 , b35 , b16 ), (b12 , b23 , b34 , b25 ), (b12 , b23 , b34 , b26 ), (b12 , b23 , b35 , b26 ), (b12 , b23 , b34 , b35 ), (b12 , b23 , b34 , b36 ), (b12 , b23 , b35 , b36 ).2.9. CB Experiment
- Definition 1.28 CB experiment: A CB experiment is a B experiment that describes the things as the tossing of M sided N dice taken V at a time in which vth die characterized in the first way or second way or both way. It is denoted by
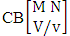 (read CB experiment of M sided N dice taken V at a time in which vth dice characterized). Example 1.24: Write the CB experiment of tossing 5 sided 4 dice taken 3 at a time in which 2nd die characterized.Solution: The desired symbol is
(read CB experiment of M sided N dice taken V at a time in which vth dice characterized). Example 1.24: Write the CB experiment of tossing 5 sided 4 dice taken 3 at a time in which 2nd die characterized.Solution: The desired symbol is 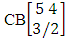 .
.2.10. CB Related Experiments
- The CB related experiments are CSB experiment, CAB experiment, CSAB experiment, CASB experiment, first way CB experiment, second way CB experiment, both way CB experiment, first way CSB experiment, second way CSB experiment, both way CSB experiment, first way CAB experiment, second way CAB experiment, both way CAB experiment, first way CB experiment, second way CB experiment, both way CB experiment, first way CSAB experiment, second way CSAB experiment, both way CSAB experiment, first way CASB experiment, second way CASB experiment, both way CASB experiment.
2.11. CB Space
- Definition 1.29 CB space: A CB space is a set of all possible outcomes of the CB experiment
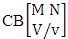 . It is denoted by
. It is denoted by 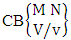 (read CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.25: Find the CB space against the CB experiment
(read CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.25: Find the CB space against the CB experiment 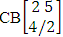 where given second die characterized in the second way.Solution: The desired CB space chosen first way arranged and second way selected is
where given second die characterized in the second way.Solution: The desired CB space chosen first way arranged and second way selected is 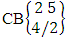 = (b11 , b12 , b13 , b14 ), (b11, b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), ( b21 , b22 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b22 , b13 , b15 ), (b11 , b22 , b13 , b25 ), (b11 , b22 , b23 , b15 ), (b11 , b22 , b23 , b25 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b24 , b15 ), (b11 , b13 , b24 , b25 ), (b11 , b23 , b14 , b15 ), (b11 , b23 , b14 , b25 ), (b11 , b23 , b24 , b15 ), (b11 , b23 , b24 , b25 ), (b21 , b13 , b14 , b15 ), (b21 , b13 , b14 , b25 ), (b21 , b13 , b24 , b15 ), (b21 , b13 , b24 , b25 ), (b21 , b23 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), ( b21 , b23 , b24 , b25 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b24 , b25 ), (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b25 ), (b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 ).
= (b11 , b12 , b13 , b14 ), (b11, b12 , b13 , b24 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), ( b21 , b22 , b23 , b24 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b23 , b15 ), (b11 , b12 , b23 , b25 ), (b11 , b22 , b13 , b15 ), (b11 , b22 , b13 , b25 ), (b11 , b22 , b23 , b15 ), (b11 , b22 , b23 , b25 ), (b21 , b12 , b13 , b15 ), (b21 , b12 , b13 , b25 ), (b21 , b12 , b23 , b15 ), (b21 , b12 , b23 , b25 ), (b21 , b22 , b13 , b15 ), (b21 , b22 , b13 , b25 ), (b21 , b22 , b23 , b15 ), (b21 , b22 , b23 , b25 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b22 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b24 , b15 ), (b11 , b13 , b24 , b25 ), (b11 , b23 , b14 , b15 ), (b11 , b23 , b14 , b25 ), (b11 , b23 , b24 , b15 ), (b11 , b23 , b24 , b25 ), (b21 , b13 , b14 , b15 ), (b21 , b13 , b14 , b25 ), (b21 , b13 , b24 , b15 ), (b21 , b13 , b24 , b25 ), (b21 , b23 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b21 , b23 , b24 , b15 ), ( b21 , b23 , b24 , b25 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b25 ), (b12 , b13 , b24 , b15 ), (b12 , b13 , b24 , b25 ), (b12 , b23 , b14 , b15 ), (b12 , b23 , b14 , b25 ), (b12 , b23 , b24 , b15 ), (b12 , b23 , b24 , b25 ), (b22 , b13 , b14 , b15 ), (b22 , b13 , b14 , b25 ), (b22 , b13 , b24 , b15 ), (b22 , b13 , b24 , b25 ), (b22 , b23 , b14 , b15 ), (b22 , b23 , b14 , b25 ), (b22 , b23 , b24 , b15 ), (b22 , b23 , b24 , b25 ).2.12. CB Related Spaces
- Definition 1.30 CSB space: A CSB space is a set of all possible outcomes of the CSB experiment
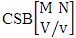 . It is denoted by
. It is denoted by 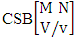 (read CSB space of M sided N dice taken V at a time in which vth die characterized).Example 1.26: Find the CSB space against the CSB experiment
(read CSB space of M sided N dice taken V at a time in which vth die characterized).Example 1.26: Find the CSB space against the CSB experiment 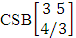 where given third die characterized in the second way.Solution: The desired CSB space is
where given third die characterized in the second way.Solution: The desired CSB space is 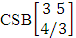 = (b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33 , b34 ), (b11 , b22 , b23 , b24 ), (b11 , b22 , b23 , b34 ), (b11 , b22 , b33 , b34 ), (b11 , b32 , b33 , b34 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b23, b34 ), (b21 , b22 , b33 , b34 ), (b21 , b32 , b33 , b34 ), (b31 , b32 , b33 , b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35), (b11 , b22 , b33 , b35 ), (b11 , b32 , b33 , b35 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b35 ), (b21 , b22 , b33 , b35 ), (b21 , b32 , b33 , b35 ), (b31 , b32 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 ), (b11 , b32 , b34 , b35 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b35 ), (b21 , b22 , b34 , b35), (b21 , b32 , b34 , b35 ), (b31 , b32 , b34 , b35 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b35 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b35 ), (b11 , b13 , b34 , b35 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b35 ), (b11 , b23 , b34 , b35 ), (b11 , b33 , b34 , b35 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b34 , b35 ), (b21 , b33 , b34 , b35 ), (b31 , b33 , b34 , b35 ), (b12 , b13 , b14 , b15), (b12 , b13 , b14 , b25 ), (b12 , b13 , b14 , b35 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b35 ), (b12 , b13 , b34 , b35 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b34 , b35 ), (b12 , b33 , b34 , b35 ), (b22 , b23 , b24 , b25 ), (b22 , b23 ,b24 , b35 ), (b22 , b23 , b34 , b35 ), (b22 , b33 , b34 , b35 ), (b32 , b33 , b34 , b35 ).Definition 1.31 CAB space: A CAB space is a set of all possible outcomes of the CAB experiment
= (b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b23 , b34 ), (b11 , b12 , b33 , b34 ), (b11 , b22 , b23 , b24 ), (b11 , b22 , b23 , b34 ), (b11 , b22 , b33 , b34 ), (b11 , b32 , b33 , b34 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b23, b34 ), (b21 , b22 , b33 , b34 ), (b21 , b32 , b33 , b34 ), (b31 , b32 , b33 , b34 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b35 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b35 ), (b11 , b12 , b33 , b35 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b35), (b11 , b22 , b33 , b35 ), (b11 , b32 , b33 , b35 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b35 ), (b21 , b22 , b33 , b35 ), (b21 , b32 , b33 , b35 ), (b31 , b32 , b33 , b35 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b35 ), (b11 , b12 , b24 , b25 ), (b11 , b12 , b24 , b35 ), (b11 , b12 , b34 , b35 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b35 ), (b11 , b22 , b34 , b35 ), (b11 , b32 , b34 , b35 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b35 ), (b21 , b22 , b34 , b35), (b21 , b32 , b34 , b35 ), (b31 , b32 , b34 , b35 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b35 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b35 ), (b11 , b13 , b34 , b35 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b35 ), (b11 , b23 , b34 , b35 ), (b11 , b33 , b34 , b35 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b35 ), (b21 , b23 , b34 , b35 ), (b21 , b33 , b34 , b35 ), (b31 , b33 , b34 , b35 ), (b12 , b13 , b14 , b15), (b12 , b13 , b14 , b25 ), (b12 , b13 , b14 , b35 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b35 ), (b12 , b13 , b34 , b35 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b35 ), (b12 , b23 , b34 , b35 ), (b12 , b33 , b34 , b35 ), (b22 , b23 , b24 , b25 ), (b22 , b23 ,b24 , b35 ), (b22 , b23 , b34 , b35 ), (b22 , b33 , b34 , b35 ), (b32 , b33 , b34 , b35 ).Definition 1.31 CAB space: A CAB space is a set of all possible outcomes of the CAB experiment 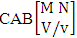 . It is denoted by
. It is denoted by 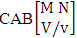 (read CAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.27: Find the CAB space against the CAB experiment
(read CAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.27: Find the CAB space against the CAB experiment 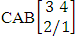 where given first die characterized in the first way.Solution: The desired CAB space chosen first way arranged and second way selected is
where given first die characterized in the first way.Solution: The desired CAB space chosen first way arranged and second way selected is 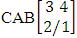 = (b11 ,b12 ), (b11 ,b13 ), (b11 ,b14 ), (b12 , b11 ), (b12 , b13 ), (b12 ,b14 ), (b13 ,b11 ), (b13 , b12 ), (b13 , b14 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b11 , b22 ), (b11 , b23 ), (b11 , b24 ), (b12 , b21 ), (b12 , b23 ), (b12 , b24 ), (b13 , b21 ), (b13 , b22 ), (b13 , b24 ), (b14 , b21 ), (b14 , b22 ), (b14 , b23 ), (b11 , b32 ), (b11 , b33 ), (b11 , b34 ), (b12 , b31), (b12 , b33 ), (b12, b34 ), (b13 , b31 ), (b13 , b32 ), (b13 , b34 ), (b14, b31 ), (b14 , b32 ), (b14 , b33 ), (b21 ,b12 ), (b21, b13 ), (b21 ,b14 ), (b22 , b11 ), (b22 , b13 ), (b22 , b14 ), (b23 , b11 ), (b23 , b12 ), (b23 , b14 ), (b24 , b11 ), (b24 , b12 ), (b24 , b13 ), (b21 , b22 ), (b21 , b23 ), (b21 , b24 ), (b22 , b21), (b22 , b23 ), (b22 , b24 ), (b23 , b21 ), (b23 , b22 ), (b23 , b24 ), (b24 , b21), (b24 , b22 ), (b24 , b23 ), (b21 , b32 ), (b21 , b33 ), (b21 , b34), (b22 , b31 ), (b22 , b33 ), (b22 , b34 ), (b23 , b31), (b23 , b32 ), (b23 , b34 ), (b24 , b31 ), (b24 , b32 ), (b24 ,b33 ), (b31 , b12), (b31 , b13), (b31 ,b14 ), (b32 , b11 ), (b32 , b13 ), (b32 , b14 ), (b33 , b11 ), (b33 , b12 ), (b33 , b14 ), (b34 , b11 ), (b34 , b12 ), (b34 , b13 ), (b31 , b22 ), (b31 , b23 ), (b31 , b24 ), (b32 , b21 ), (b32 , b23 ), (b32 , b24 ), (b33 , b21 ), (b33 , b22 ), (b33 , b24 ), (b34 , b21 ), (b34 , b22 ), (b34 , b23 ), (b31 , b32 ), (b31 , b33), (b31 , b34 ), (b32 , b31 ), (b32 , b33 ), (b32 , b34 ), (b33 , b31 ), (b33 , b32 ), (b33 , b34 ), (b34 , b31 ), (b34 , b32 ), (b34 , b33 ).Definition 1.32 CSAB space: A CSAB space is a set of all possible outcomes of the CSAB experiment
= (b11 ,b12 ), (b11 ,b13 ), (b11 ,b14 ), (b12 , b11 ), (b12 , b13 ), (b12 ,b14 ), (b13 ,b11 ), (b13 , b12 ), (b13 , b14 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b11 , b22 ), (b11 , b23 ), (b11 , b24 ), (b12 , b21 ), (b12 , b23 ), (b12 , b24 ), (b13 , b21 ), (b13 , b22 ), (b13 , b24 ), (b14 , b21 ), (b14 , b22 ), (b14 , b23 ), (b11 , b32 ), (b11 , b33 ), (b11 , b34 ), (b12 , b31), (b12 , b33 ), (b12, b34 ), (b13 , b31 ), (b13 , b32 ), (b13 , b34 ), (b14, b31 ), (b14 , b32 ), (b14 , b33 ), (b21 ,b12 ), (b21, b13 ), (b21 ,b14 ), (b22 , b11 ), (b22 , b13 ), (b22 , b14 ), (b23 , b11 ), (b23 , b12 ), (b23 , b14 ), (b24 , b11 ), (b24 , b12 ), (b24 , b13 ), (b21 , b22 ), (b21 , b23 ), (b21 , b24 ), (b22 , b21), (b22 , b23 ), (b22 , b24 ), (b23 , b21 ), (b23 , b22 ), (b23 , b24 ), (b24 , b21), (b24 , b22 ), (b24 , b23 ), (b21 , b32 ), (b21 , b33 ), (b21 , b34), (b22 , b31 ), (b22 , b33 ), (b22 , b34 ), (b23 , b31), (b23 , b32 ), (b23 , b34 ), (b24 , b31 ), (b24 , b32 ), (b24 ,b33 ), (b31 , b12), (b31 , b13), (b31 ,b14 ), (b32 , b11 ), (b32 , b13 ), (b32 , b14 ), (b33 , b11 ), (b33 , b12 ), (b33 , b14 ), (b34 , b11 ), (b34 , b12 ), (b34 , b13 ), (b31 , b22 ), (b31 , b23 ), (b31 , b24 ), (b32 , b21 ), (b32 , b23 ), (b32 , b24 ), (b33 , b21 ), (b33 , b22 ), (b33 , b24 ), (b34 , b21 ), (b34 , b22 ), (b34 , b23 ), (b31 , b32 ), (b31 , b33), (b31 , b34 ), (b32 , b31 ), (b32 , b33 ), (b32 , b34 ), (b33 , b31 ), (b33 , b32 ), (b33 , b34 ), (b34 , b31 ), (b34 , b32 ), (b34 , b33 ).Definition 1.32 CSAB space: A CSAB space is a set of all possible outcomes of the CSAB experiment 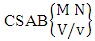 . It is denoted by
. It is denoted by 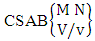 (read CSAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.28: Find the CSAB space against the CSAB experiment
(read CSAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.28: Find the CSAB space against the CSAB experiment 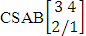 where given first die characterized in the first way.Solution: The desired CSAB space is
where given first die characterized in the first way.Solution: The desired CSAB space is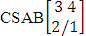 = (b11 ,b12 ), (b11 , b13 ), (b11 ,b14 ), (b12 ,b11 ), (b12 ,b13 ), (b12 ,b14 ), (b13 ,b11), (b13 , b12 ), (b13 , b14 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b11 , b22 ), (b11 , b23 ), (b11 , b24 ), (b12 , b21 ), (b12 , b23 ), (b12 , b24 ), (b13 , b21 ), (b13 , b22 ), (b13 , b24 ), (b14 , b21 ), (b14 , b22 ), (b14 , b23 ), (b11 , b32 ), (b11, b33 ), (b11 , b34 ), (b12 , b31 ), (b12 , b33 ), (b12, b34 ), (b13 , b31 ), (b13 , b32 ), (b13 , b34 ), (b14, b31 ), (b14 , b32 ), (b14 , b33 ), (b21 , b22), (b21, b23 ), (b21 , b24), (b22 , b21), (b22 , b23 ), (b22 , b24 ), (b23 , b21), (b23 , b22), (b23 , b24 ), (b24, b21 ), (b24 , b22 ), (b24 , b23 ), (b21 , b32 ), (b21, b33 ), (b21 , b34 ), (b22 , b31), (b22 , b33 ), (b22 , b34 ), (b23 , b31 ), (b23 , b32 ), (b23 , b34 ), (b24, b31), (b24 , b32 ), (b24 , b33 ), (b31 ,b32 ), (b31, b33 ), (b31 , b34 ), (b32 , b31 ), (b32 , b33 ), (b32, b34 ), (b33 , b31 ), (b33, b32 ), (b33 , b34 ), (b34, b31 ), (b34 , b32 ), (b34, b33 ).Definition 1.33 CASB space: A CASB space is a set of all possible outcomes of the CASB experiment
= (b11 ,b12 ), (b11 , b13 ), (b11 ,b14 ), (b12 ,b11 ), (b12 ,b13 ), (b12 ,b14 ), (b13 ,b11), (b13 , b12 ), (b13 , b14 ), (b14 , b11 ), (b14 , b12 ), (b14 , b13 ), (b11 , b22 ), (b11 , b23 ), (b11 , b24 ), (b12 , b21 ), (b12 , b23 ), (b12 , b24 ), (b13 , b21 ), (b13 , b22 ), (b13 , b24 ), (b14 , b21 ), (b14 , b22 ), (b14 , b23 ), (b11 , b32 ), (b11, b33 ), (b11 , b34 ), (b12 , b31 ), (b12 , b33 ), (b12, b34 ), (b13 , b31 ), (b13 , b32 ), (b13 , b34 ), (b14, b31 ), (b14 , b32 ), (b14 , b33 ), (b21 , b22), (b21, b23 ), (b21 , b24), (b22 , b21), (b22 , b23 ), (b22 , b24 ), (b23 , b21), (b23 , b22), (b23 , b24 ), (b24, b21 ), (b24 , b22 ), (b24 , b23 ), (b21 , b32 ), (b21, b33 ), (b21 , b34 ), (b22 , b31), (b22 , b33 ), (b22 , b34 ), (b23 , b31 ), (b23 , b32 ), (b23 , b34 ), (b24, b31), (b24 , b32 ), (b24 , b33 ), (b31 ,b32 ), (b31, b33 ), (b31 , b34 ), (b32 , b31 ), (b32 , b33 ), (b32, b34 ), (b33 , b31 ), (b33, b32 ), (b33 , b34 ), (b34, b31 ), (b34 , b32 ), (b34, b33 ).Definition 1.33 CASB space: A CASB space is a set of all possible outcomes of the CASB experiment 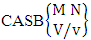 . It is denoted by
. It is denoted by 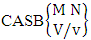 (read CASB space of M sided N dice taken V at a time in which vth die characterized).Example 1.29: Find the CASB space against the CASB experiment CASB
(read CASB space of M sided N dice taken V at a time in which vth die characterized).Example 1.29: Find the CASB space against the CASB experiment CASB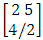 where given second die characterized in the second way.Solution: This solution is worked out in the solution of the example 1.25.The following discusses three kinds of CB spaces i.e., first way CB space, second way CB space and both way CB space with their different forms.Definition 1.34 First way CB space: A first way CB space is a set of all possible outcomes of the first way CB experiment
where given second die characterized in the second way.Solution: This solution is worked out in the solution of the example 1.25.The following discusses three kinds of CB spaces i.e., first way CB space, second way CB space and both way CB space with their different forms.Definition 1.34 First way CB space: A first way CB space is a set of all possible outcomes of the first way CB experiment 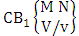 . It is denoted by
. It is denoted by 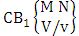 (read first way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.30: Find the first way CB space against the first way CB experiment
(read first way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.30: Find the first way CB space against the first way CB experiment 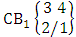 where given first die characterized in the first way.Solution: Suppose the desired CB space chosen both way arranged. So the first way CB space
where given first die characterized in the first way.Solution: Suppose the desired CB space chosen both way arranged. So the first way CB space 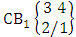 worked out in example 1.27.Definition 1.35 Second way CB space: A second way CB space is a set of all possible outcomes of the second way CB experiment
worked out in example 1.27.Definition 1.35 Second way CB space: A second way CB space is a set of all possible outcomes of the second way CB experiment 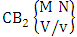 . It is denoted by
. It is denoted by 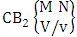 (read second way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.31: Find the second way CB space against the second way CB experiment
(read second way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.31: Find the second way CB space against the second way CB experiment 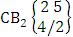 where given second die characterized in the second way.Solution: Suppose the desired CB space chosen first way arranged and second way selected so the second way CB space
where given second die characterized in the second way.Solution: Suppose the desired CB space chosen first way arranged and second way selected so the second way CB space 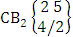 worked out in example 1.25.Definition 1.36 Both way CB space: A both way CB space is a set of all possible outcomes of the both way CB experiment
worked out in example 1.25.Definition 1.36 Both way CB space: A both way CB space is a set of all possible outcomes of the both way CB experiment 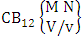 . It is denoted by
. It is denoted by 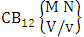 (read both way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.32: Find the both way CB space against the both way CB experiment
(read both way CB space of M sided N dice taken V at a time in which vth die characterized).Example 1.32: Find the both way CB space against the both way CB experiment 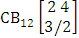 where given second die characterized in the both way.Solution: Suppose the desired CB space chosen first way arranged and second way selected so the both way CB space is
where given second die characterized in the both way.Solution: Suppose the desired CB space chosen first way arranged and second way selected so the both way CB space is 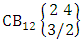 = (b11, b12 , b13), (b11, b12 , b14), (b11 , b12 , b23), (b11, b12 , b24), (b11 ,b13 , b14), (b11, b13 , b24), (b12, b13 , b14), (b12, b13, b24 ), (b11 , b22 , b13), (b11, b22 , b14), (b11 , b22 , b23 ), (b11, b22 , b24 ), (b11 , b23 , b14 ), (b11 , b23 , b24), (b12 , b23 , b14), (b12, b23 , b24), (b21 , b12 , b13 ), (b21 , b12 , b14), (b21 , b12 , b23), (b21 , b12 , b24), (b21 , b13 , b14), (b21 , b13 , b24 ), (b22 , b13 , b14 ), (b22 , b13 , b24), (b21 , b22 ,b13), (b21 , b22 , b14), (b21 , b22 , b23 ), (b21 , b22 , b24), (b21 , b23 , b14), (b21 , b23 , b24), (b22 , b23 , b14), (b22 , b23 , b24).Definition 1.37 First way CSB space: A first way CSB space is a set of all possible outcomes of the first way CSB experiment
= (b11, b12 , b13), (b11, b12 , b14), (b11 , b12 , b23), (b11, b12 , b24), (b11 ,b13 , b14), (b11, b13 , b24), (b12, b13 , b14), (b12, b13, b24 ), (b11 , b22 , b13), (b11, b22 , b14), (b11 , b22 , b23 ), (b11, b22 , b24 ), (b11 , b23 , b14 ), (b11 , b23 , b24), (b12 , b23 , b14), (b12, b23 , b24), (b21 , b12 , b13 ), (b21 , b12 , b14), (b21 , b12 , b23), (b21 , b12 , b24), (b21 , b13 , b14), (b21 , b13 , b24 ), (b22 , b13 , b14 ), (b22 , b13 , b24), (b21 , b22 ,b13), (b21 , b22 , b14), (b21 , b22 , b23 ), (b21 , b22 , b24), (b21 , b23 , b14), (b21 , b23 , b24), (b22 , b23 , b14), (b22 , b23 , b24).Definition 1.37 First way CSB space: A first way CSB space is a set of all possible outcomes of the first way CSB experiment 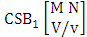 . It is denoted by
. It is denoted by 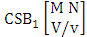 (read first way CSB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.38 Second way CSB space: A second way CSB space is a set of all possible outcomes of the second way CSB experiment
(read first way CSB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.38 Second way CSB space: A second way CSB space is a set of all possible outcomes of the second way CSB experiment 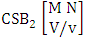 . It is denoted by
. It is denoted by 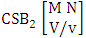 (read second way CSB space of M sided N dice taken V at a time in which vth die characterized). Definition 1.39 Both way CSB space: A both way CSB space is a set of all possible outcomes of the both way CSB experiment
(read second way CSB space of M sided N dice taken V at a time in which vth die characterized). Definition 1.39 Both way CSB space: A both way CSB space is a set of all possible outcomes of the both way CSB experiment 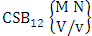 . It is denoted by
. It is denoted by 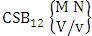 (read both way CSB space of M sided N dice taken V at a time in which vth die characterized).Example 1.33: Find the both way CSB space against the both way CSB experiment
(read both way CSB space of M sided N dice taken V at a time in which vth die characterized).Example 1.33: Find the both way CSB space against the both way CSB experiment 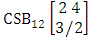 . Solution: The desired CSB space is
. Solution: The desired CSB space is 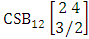 = (b11 , b12 , b13), (b11 , b12 , b14), (b11 , b12 , b23), (b11 , b12 , b24), (b11 , b13 , b14), (b11 , b13 , b24),(b12 , b13 , b14 ), (b12 , b13 , b24), (b11 , b22 , b23), (b11 , b22 , b24), (b11 , b23 , b24), (b12 ,b23 , b24), (b21 ,b22 , b23 ), (b21 , b22 ,b24), (b21 , b23 , b24 ), (b22 , b23 , b24 ).Definition 1.40 First way CAB space: A first way CAB space is a set of all possible outcomes of the first way CAB experiment
= (b11 , b12 , b13), (b11 , b12 , b14), (b11 , b12 , b23), (b11 , b12 , b24), (b11 , b13 , b14), (b11 , b13 , b24),(b12 , b13 , b14 ), (b12 , b13 , b24), (b11 , b22 , b23), (b11 , b22 , b24), (b11 , b23 , b24), (b12 ,b23 , b24), (b21 ,b22 , b23 ), (b21 , b22 ,b24), (b21 , b23 , b24 ), (b22 , b23 , b24 ).Definition 1.40 First way CAB space: A first way CAB space is a set of all possible outcomes of the first way CAB experiment 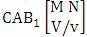 . It is denoted by
. It is denoted by 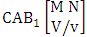 (read first way CAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.41 Second way CAB space: A second way CAB space is a set of all possible outcomes of the second way CAB experiment
(read first way CAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.41 Second way CAB space: A second way CAB space is a set of all possible outcomes of the second way CAB experiment 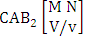 . It is denoted by
. It is denoted by 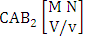 (read second way CAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.42 Both way CAB space: A both way CAB space is a set of all possible outcomes of the both way CAB experiment
(read second way CAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.42 Both way CAB space: A both way CAB space is a set of all possible outcomes of the both way CAB experiment 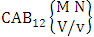 . It is denoted by
. It is denoted by 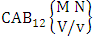 (read both way CAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.34: Find the both way CAB space against the both way CAB experiment
(read both way CAB space of M sided N dice taken V at a time in which vth die characterized).Example 1.34: Find the both way CAB space against the both way CAB experiment 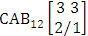 . Solution: The desired CAB space is
. Solution: The desired CAB space is 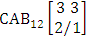 = (b11 , b12), (b11 , b13), (b11 , b22), (b11 , b23), (b11 , b32), (b11, b33), (b12 , b11 ), (b12, b13 ), (b12 , b21 ), (b12 , b23 ), (b12 , b31), (b12 , b33 ), (b13, b11), (b13, b12 ), (b13, b21 ), (b13 , b22 ), (b13 , b31 ), (b13, b32 ), (b21, b12 ), (b21, b13 ), (b21 , b22 ), (b21, b23 ), (b21 , b32 ), (b21 , b33 ), (b22 , b11 ), (b22 , b13 ), (b22 , b21 ), (b22 , b23 ), (b22 , b31), (b22 , b33 ), (b23 , b11 ), (b23 , b12 ), (b23 , b21), (b23 , b22), (b23 , b31), (b23 , b32), (b31, b12), (b31 , b13 ), (b31 , b22 ), (b31 , b23 ), (b31, b32), (b31 , b33 ), (b32 , b11 ), (b32, b13 ), (b32 , b21), (b32 , b23 ), (b32 , b31), (b32 , b33 ), (b33, b11), (b33, b12 ), (b33 , b21 ), (b33, b22 ), (b33, b31 ), (b33 , b32 ).Definition 1.43 First way CSAB space: A first way CSAB space is a set of all possible outcomes of the first way CSAB experiment
= (b11 , b12), (b11 , b13), (b11 , b22), (b11 , b23), (b11 , b32), (b11, b33), (b12 , b11 ), (b12, b13 ), (b12 , b21 ), (b12 , b23 ), (b12 , b31), (b12 , b33 ), (b13, b11), (b13, b12 ), (b13, b21 ), (b13 , b22 ), (b13 , b31 ), (b13, b32 ), (b21, b12 ), (b21, b13 ), (b21 , b22 ), (b21, b23 ), (b21 , b32 ), (b21 , b33 ), (b22 , b11 ), (b22 , b13 ), (b22 , b21 ), (b22 , b23 ), (b22 , b31), (b22 , b33 ), (b23 , b11 ), (b23 , b12 ), (b23 , b21), (b23 , b22), (b23 , b31), (b23 , b32), (b31, b12), (b31 , b13 ), (b31 , b22 ), (b31 , b23 ), (b31, b32), (b31 , b33 ), (b32 , b11 ), (b32, b13 ), (b32 , b21), (b32 , b23 ), (b32 , b31), (b32 , b33 ), (b33, b11), (b33, b12 ), (b33 , b21 ), (b33, b22 ), (b33, b31 ), (b33 , b32 ).Definition 1.43 First way CSAB space: A first way CSAB space is a set of all possible outcomes of the first way CSAB experiment 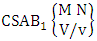 . It is denoted by
. It is denoted by 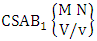 (read first way CSAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.44 Second way CSAB space: A second way CSAB space is a set of all possible outcomes of the second way CSAB experiment
(read first way CSAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.44 Second way CSAB space: A second way CSAB space is a set of all possible outcomes of the second way CSAB experiment 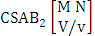 . It is denoted by
. It is denoted by 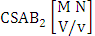 (read second way CSAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.45 Both way CSAB space: A both way CSAB space is a set of all possible outcomes of the both way CSAB experiment
(read second way CSAB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.45 Both way CSAB space: A both way CSAB space is a set of all possible outcomes of the both way CSAB experiment 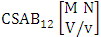 . It is denoted by
. It is denoted by 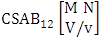 (read both way CSAB space of M sided N dice taken V at a time in which vth die characterized). Example 1.35: Find the both way CSAB space against the both way CSAB experiment
(read both way CSAB space of M sided N dice taken V at a time in which vth die characterized). Example 1.35: Find the both way CSAB space against the both way CSAB experiment 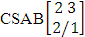 .Solution: The desired CSAB space is
.Solution: The desired CSAB space is 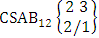 = (b11, b12 ), (b11, b13 ), (b11 , b22 ), (b11, b23 ), (b12, b11 ), (b12 , b13 ), (b12 , b21 ), (b12 , b23 ), (b13, b11 ), (b13, b12 ), (b13, b21 ), (b13 , b22 ), (b21 , b22), (b21 , b23 ), (b22 , b21 ), (b22 , b23 ), (b23 , b21), (b23 , b22 ).Definition 1.46 First way CASB space: A first way CASB space is a set of all possible outcomes of the first way CASB experiment
= (b11, b12 ), (b11, b13 ), (b11 , b22 ), (b11, b23 ), (b12, b11 ), (b12 , b13 ), (b12 , b21 ), (b12 , b23 ), (b13, b11 ), (b13, b12 ), (b13, b21 ), (b13 , b22 ), (b21 , b22), (b21 , b23 ), (b22 , b21 ), (b22 , b23 ), (b23 , b21), (b23 , b22 ).Definition 1.46 First way CASB space: A first way CASB space is a set of all possible outcomes of the first way CASB experiment 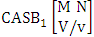 . It is denoted by
. It is denoted by 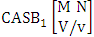 (read first way CASB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.47 Second way CASB space: A second way CASB space is a set of all possible outcomes of the second way CASB experiment
(read first way CASB space of M sided N dice taken V at a time in which vth die characterized).Definition 1.47 Second way CASB space: A second way CASB space is a set of all possible outcomes of the second way CASB experiment 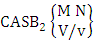 . It is denoted by
. It is denoted by 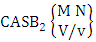 (read second way CASB space of M sided N dice taken V at a time in which vth die characterized). Definition 1.48 Both way CASB space: A both way CASB space is a set of all possible outcomes of the both way CASB experiment
(read second way CASB space of M sided N dice taken V at a time in which vth die characterized). Definition 1.48 Both way CASB space: A both way CASB space is a set of all possible outcomes of the both way CASB experiment 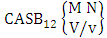 . It it denoted by
. It it denoted by 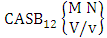 (read both way CASB space of M sided N dice taken V at a time in which vth die characterized).Example 1.36: Find the both way CASB space against the both way CASB experiment
(read both way CASB space of M sided N dice taken V at a time in which vth die characterized).Example 1.36: Find the both way CASB space against the both way CASB experiment 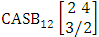 .Solution: This solution is worked out in the solution of example 1.32.
.Solution: This solution is worked out in the solution of example 1.32.2.13. GB Experiment
- Definition 1.49 GB experiment: A GB experiment is a B experiment that describes the thing as the tossing of M sided N dice taken V at a time in which X ; min(M, U) − M + 1 ≤ X ≤ min(M, U, V) is observed in the first way for M ≥ U or Y ; min(N, U) − N + V ≤ Y ≤ min(N, U, V) is observed in the second way for N ≥ U or X, Y are observed in the both way at a time. It is denoted by
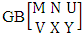 (read GB experiment of M sided N dice taken V at a time where X, Y are observed for U).Example 1.37: Denote the GB experiment of 5 sided 6 dice taken 4 at a time where 2 is observed for 3.Solution: The desired symbol is
(read GB experiment of M sided N dice taken V at a time where X, Y are observed for U).Example 1.37: Denote the GB experiment of 5 sided 6 dice taken 4 at a time where 2 is observed for 3.Solution: The desired symbol is 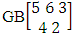 .
.2.14. GB Related Experiments
- The GB related experiments are GSB experiment, GAB experiment, GSAB experiment, GASB experiment, first way GB experiment, second way GB experiment, both way GB experiment, first way GSB experiment, second way GSB experiment, both way GSB experiment, first way GAB experiment, second way GAB experiment, both way GAB experiment, first way GB experiment, second way GB experiment, both way GB experiment, first way GSAB experiment, second way GSAB experiment, both way GSAB experiment, first way GASB experiment, second way GASB experiment, both way GASB experiment.
2.15. GB Space
- Definition 1.50 GB space: A GB space is a set of all possible outcomes of the GB experiment
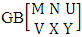 . It is denoted by
. It is denoted by 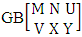 (read GB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.38: Find the GB space against the GB experiment
(read GB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.38: Find the GB space against the GB experiment 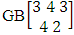 where 2 is observed in the first way.Solution: Let the GB space chosen first way arranged and second way selected then
where 2 is observed in the first way.Solution: Let the GB space chosen first way arranged and second way selected then 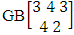 = (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b33 , b14 ), (b11 , b12 , b33 , b34 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b11 , b32 , b13 , b14 ), (b11 , b32 , b13 , b34 ), (b11 , b32 , b33 , b14 ), (b11 , b32 , b33 , b34 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b33 , b24), (b21 , b22 , b33 , b34 ), (b21 , b32 , b23 , b24 ), (b21 , b32 , b23 , b34 ), (b21 , b32 , b33 , b24 ), (b21 , b32 , b33 , b34 ), (b31 , b12 , b13 , b14 ), (b31 , b12 , b13 , b34 ), (b31 , b12 , b33, b14 ), (b31 , b12 , b33 , b34 ), (b31 , b22 , b23 , b24), (b31 , b22 , b23 , b34), (b31 , b22 , b33 , b24 ), (b31 , b22 , b33 , b34 ), (b31 , b32 , b13 , b14 ), (b31 , b32 , b13 , b34), (b31 , b32 , b23 , b24 ), (b31 , b32 , b23 , b34 ), (b31 , b32 , b33 , b14 ), (b31 , b32 , b33 , b24 ).
= (b11 , b12 , b13 , b24 ), (b11 , b12 , b13 , b34 ), (b11 , b12 , b23 , b14 ), (b11 , b12 , b23 , b24 ), (b11 , b12 , b33 , b14 ), (b11 , b12 , b33 , b34 ), (b11 , b22 , b13 , b14 ), (b11 , b22 , b13 , b24 ), (b11 , b22 , b23 , b14 ), (b11 , b22 , b23 , b24 ), (b11 , b32 , b13 , b14 ), (b11 , b32 , b13 , b34 ), (b11 , b32 , b33 , b14 ), (b11 , b32 , b33 , b34 ), (b21 , b12 , b13 , b14 ), (b21 , b12 , b13 , b24 ), (b21 , b12 , b23 , b14 ), (b21 , b12 , b23 , b24 ), (b21 , b22 , b13 , b14 ), (b21 , b22 , b13 , b24 ), (b21 , b22 , b23 , b14 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b33 , b24), (b21 , b22 , b33 , b34 ), (b21 , b32 , b23 , b24 ), (b21 , b32 , b23 , b34 ), (b21 , b32 , b33 , b24 ), (b21 , b32 , b33 , b34 ), (b31 , b12 , b13 , b14 ), (b31 , b12 , b13 , b34 ), (b31 , b12 , b33, b14 ), (b31 , b12 , b33 , b34 ), (b31 , b22 , b23 , b24), (b31 , b22 , b23 , b34), (b31 , b22 , b33 , b24 ), (b31 , b22 , b33 , b34 ), (b31 , b32 , b13 , b14 ), (b31 , b32 , b13 , b34), (b31 , b32 , b23 , b24 ), (b31 , b32 , b23 , b34 ), (b31 , b32 , b33 , b14 ), (b31 , b32 , b33 , b24 ).2.16. GB Related Spaces
- Definition 1.51 GSB space: A GSB space is a set of all possible outcomes of the GSB experiment
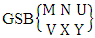 . It is denoted by
. It is denoted by 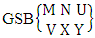 (read GSB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.39: Find the GSB space against the GSB experiment
(read GSB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.39: Find the GSB space against the GSB experiment 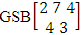 where 3 is observed in the second way.Solution: Let the components of limited size are 1, 2, 3 and 4. Now the GSB space is
where 3 is observed in the second way.Solution: Let the components of limited size are 1, 2, 3 and 4. Now the GSB space is 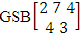 = (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16), (b11 , b13 , b14 , b17 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b26 ), (b11 , b12 , b13 , b27 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b26 ), (b11 , b12 , b14 , b27 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b26 ), (b11 , b13 , b14 , b27 ), (b12 , b13 , b14 , b26 ), ( b12 , b13 , b14 , b26 ), (b12 , b13 , b14 , b27 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b26 ), (b11 , b12 , b23 , b27 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b26 ), (b11 , b12 , b24 , b27 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b26 ), (b11 , b13 , b24 , b27 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b26 ), (b12 , b13 , b24 , b27 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b26 ), (b11 , b22 , b23 , b27 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b26 ), (b11 , b22 , b24 , b27 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b26), (b11 , b23 , b24 , b27 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b26 ), (b12 , b23 , b24 , b27 ), (b21 , b22 , b23 , b25), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b24 , b27). Definition 1.52 GAB space: A GAB space is a set of all possible outcomes of the GAB experiment
= (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16), (b11 , b13 , b14 , b17 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b11 , b12 , b13 , b25 ), (b11 , b12 , b13 , b26 ), (b11 , b12 , b13 , b27 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b14 , b26 ), (b11 , b12 , b14 , b27 ), (b11 , b13 , b14 , b25 ), (b11 , b13 , b14 , b26 ), (b11 , b13 , b14 , b27 ), (b12 , b13 , b14 , b26 ), ( b12 , b13 , b14 , b26 ), (b12 , b13 , b14 , b27 ), (b11 , b12 , b23 , b25 ), (b11 , b12 , b23 , b26 ), (b11 , b12 , b23 , b27 ), (b11 , b12 , b14 , b25 ), (b11 , b12 , b24 , b26 ), (b11 , b12 , b24 , b27 ), (b11 , b13 , b24 , b25 ), (b11 , b13 , b24 , b26 ), (b11 , b13 , b24 , b27 ), (b12 , b13 , b24 , b25 ), (b12 , b13 , b24 , b26 ), (b12 , b13 , b24 , b27 ), (b11 , b22 , b23 , b25 ), (b11 , b22 , b23 , b26 ), (b11 , b22 , b23 , b27 ), (b11 , b22 , b24 , b25 ), (b11 , b22 , b24 , b26 ), (b11 , b22 , b24 , b27 ), (b11 , b23 , b24 , b25 ), (b11 , b23 , b24 , b26), (b11 , b23 , b24 , b27 ), (b12 , b23 , b24 , b25 ), (b12 , b23 , b24 , b26 ), (b12 , b23 , b24 , b27 ), (b21 , b22 , b23 , b25), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b24 , b27). Definition 1.52 GAB space: A GAB space is a set of all possible outcomes of the GAB experiment 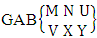 . It is denoted by
. It is denoted by 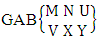 (read GAB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.40: Find the GAB space against the GAB experiment
(read GAB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.40: Find the GAB space against the GAB experiment 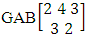 where 2 is observed in the second way.Solution: Let the components of limited size are 1, 2 and 3 and the GAB space is then
where 2 is observed in the second way.Solution: Let the components of limited size are 1, 2 and 3 and the GAB space is then 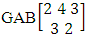 = (b11 , b12 , b14 ), (b11 , b13 , b14 ), (b11 , b14 , b12 ), (b11 , b14 , b13 ), (b13 , b11 , b14 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b12 , b11 , b14 ), (b12 , b13 , b14 ), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b11 , b12 , b24 ), (b11 , b13 , b24 ), (b11 , b14 , b22 ), (b11 , b14 , b23 ), (b13 , b11 , b24 ), (b13 , b12 , b24 ), (b13 , b14 , b21 ), (b13 , b14 , b22 ), (b12 , b11 , b24 ), (b12 , b13 , b24 ), (b12 , b14 , b21 ), (b12 , b14 , b23 ), (b14 , b11 , b22 ), (b14 , b11 , b23 ), (b14 , b12 , b21 ), (b14 , b12 , b23 ), (b14 , b13 , b21 ), (b14 , b13 , b22 ), (b11 , b22 , b14 ), (b11 , b23 , b14 ), (b11 , b24 , b12 ), (b11 , b24 , b13 ), (b13 , b21 , b14 ), (b13 , b22 , b14 ), (b13 , b24 , b11 ), (b13 , b24 , b12 ), (b12 , b21 , b14 ), (b12 , b23 , b14 ), (b12 , b24 , b11 ), (b12 , b24 , b13 ), (b14 , b21 , b12 ), (b14 , b21 , b13 ), (b14 , b22 , b11 ), (b14 , b22 , b13 ), (b14 , b23 , b11 ), (b14 , b23 , b12 ), (b11 , b22 , b24 ), (b11 , b23 , b24 ), (b11 , b24 , b22 ), (b11 , b24 , b23 ), (b13 , b21 , b24 ), (b13 , b22 , b24 ), (b13 , b24 , b21 ), (b13 , b24 , b22 ), (b12 , b21 , b24 ), (b12 , b23 , b24 ), (b12 , b24 , b21 ), (b12 , b24 , b23 ), (b14 , b21 , b22), (b14 , b21 , b23 ), (b14 , b22 , b21 ), (b14 , b22 , b23 ), (b14 , b23 , b21 ), (b14 , b23 , b22 ), (b21 , b12 , b14 ), (b21 , b13 , b14 ), (b21 , b14 , b12 ), (b21 , b14 , b13 ), (b23 , b11 , b14 ), (b23 , b12 , b14 ), (b23 , b14 , b11 ), (b23 , b14 , b12 ), (b22 , b11 , b14 ), (b22 , b13 , b14 ), (b22 , b14 , b11 ), (b22 , b14 , b13 ), (b24 , b11 , b12 ), (b24 , b11 , b13 ), (b24 , b12 , b11 ), (b24 , b12 , b13 ), (b24 , b13 , b11 ), (b24 , b13 , b12 ), (b21 , b12 , b24 ), (b21 , b13 , b24 ), (b21 , b14 , b22 ), (b21, b14 , b23 ), (b23 , b11 , b24 ), (b23 , b12 , b24 ), (b23 , b14 , b21 ), (b23 , b14 , b22 ), (b22 , b11 , b24 ), (b22, b13 , b24 ), (b22 , b14 , b21 ), (b22 , b14 , b23 ) (b24 , b11 , b22 ), (b24 , b11, b23 ), (b24 , b12 , b21 ), (b24 , b12 , b23 ), (b24 , b13 , b21 ), (b24 , b13 , b22 ), (b21 , b22 , b14 ), (b21 , b23 , b14 ), (b21 , b24 , b12 ), (b21 , b24 , b13 ), (b23 , b21 , b14 ), (b23 , b22 , b14 ), (b23 , b24 , b11 ), (b23 , b24 , b12 ), (b22 , b21 , b14 ), (b22 , b23 , b14 ), (b22 , b24 , b11 ), (b22 , b24 , b13 ), (b24 , b21 , b12 ), (b24 , b21 , b13 ), (b24 , b22 , b11 ), (b24 , b22 , b13 ), (b24 , b23 , b11 ), (b24 , b23 , b12 ), (b21 , b22 , b24 ), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b23 , b21 , b24 ), (b23 , b22 , b24 ), (b23 , b24 , b21 ), (b23 , b24 , b22 ), (b22 , b21 , b24 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b24 , b21 , b22 ), (b24 , b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.53 GSAB space: A GSAB space is a set of all possible outcomes of the GSAB experiment
= (b11 , b12 , b14 ), (b11 , b13 , b14 ), (b11 , b14 , b12 ), (b11 , b14 , b13 ), (b13 , b11 , b14 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b12 , b11 , b14 ), (b12 , b13 , b14 ), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b11 , b12 , b24 ), (b11 , b13 , b24 ), (b11 , b14 , b22 ), (b11 , b14 , b23 ), (b13 , b11 , b24 ), (b13 , b12 , b24 ), (b13 , b14 , b21 ), (b13 , b14 , b22 ), (b12 , b11 , b24 ), (b12 , b13 , b24 ), (b12 , b14 , b21 ), (b12 , b14 , b23 ), (b14 , b11 , b22 ), (b14 , b11 , b23 ), (b14 , b12 , b21 ), (b14 , b12 , b23 ), (b14 , b13 , b21 ), (b14 , b13 , b22 ), (b11 , b22 , b14 ), (b11 , b23 , b14 ), (b11 , b24 , b12 ), (b11 , b24 , b13 ), (b13 , b21 , b14 ), (b13 , b22 , b14 ), (b13 , b24 , b11 ), (b13 , b24 , b12 ), (b12 , b21 , b14 ), (b12 , b23 , b14 ), (b12 , b24 , b11 ), (b12 , b24 , b13 ), (b14 , b21 , b12 ), (b14 , b21 , b13 ), (b14 , b22 , b11 ), (b14 , b22 , b13 ), (b14 , b23 , b11 ), (b14 , b23 , b12 ), (b11 , b22 , b24 ), (b11 , b23 , b24 ), (b11 , b24 , b22 ), (b11 , b24 , b23 ), (b13 , b21 , b24 ), (b13 , b22 , b24 ), (b13 , b24 , b21 ), (b13 , b24 , b22 ), (b12 , b21 , b24 ), (b12 , b23 , b24 ), (b12 , b24 , b21 ), (b12 , b24 , b23 ), (b14 , b21 , b22), (b14 , b21 , b23 ), (b14 , b22 , b21 ), (b14 , b22 , b23 ), (b14 , b23 , b21 ), (b14 , b23 , b22 ), (b21 , b12 , b14 ), (b21 , b13 , b14 ), (b21 , b14 , b12 ), (b21 , b14 , b13 ), (b23 , b11 , b14 ), (b23 , b12 , b14 ), (b23 , b14 , b11 ), (b23 , b14 , b12 ), (b22 , b11 , b14 ), (b22 , b13 , b14 ), (b22 , b14 , b11 ), (b22 , b14 , b13 ), (b24 , b11 , b12 ), (b24 , b11 , b13 ), (b24 , b12 , b11 ), (b24 , b12 , b13 ), (b24 , b13 , b11 ), (b24 , b13 , b12 ), (b21 , b12 , b24 ), (b21 , b13 , b24 ), (b21 , b14 , b22 ), (b21, b14 , b23 ), (b23 , b11 , b24 ), (b23 , b12 , b24 ), (b23 , b14 , b21 ), (b23 , b14 , b22 ), (b22 , b11 , b24 ), (b22, b13 , b24 ), (b22 , b14 , b21 ), (b22 , b14 , b23 ) (b24 , b11 , b22 ), (b24 , b11, b23 ), (b24 , b12 , b21 ), (b24 , b12 , b23 ), (b24 , b13 , b21 ), (b24 , b13 , b22 ), (b21 , b22 , b14 ), (b21 , b23 , b14 ), (b21 , b24 , b12 ), (b21 , b24 , b13 ), (b23 , b21 , b14 ), (b23 , b22 , b14 ), (b23 , b24 , b11 ), (b23 , b24 , b12 ), (b22 , b21 , b14 ), (b22 , b23 , b14 ), (b22 , b24 , b11 ), (b22 , b24 , b13 ), (b24 , b21 , b12 ), (b24 , b21 , b13 ), (b24 , b22 , b11 ), (b24 , b22 , b13 ), (b24 , b23 , b11 ), (b24 , b23 , b12 ), (b21 , b22 , b24 ), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b23 , b21 , b24 ), (b23 , b22 , b24 ), (b23 , b24 , b21 ), (b23 , b24 , b22 ), (b22 , b21 , b24 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b24 , b21 , b22 ), (b24 , b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.53 GSAB space: A GSAB space is a set of all possible outcomes of the GSAB experiment 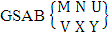 . It is denoted by
. It is denoted by  (read GSAB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.41: Find the GSAB space against the GSAB experiment
(read GSAB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.41: Find the GSAB space against the GSAB experiment 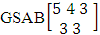 where 3 is observed in the both way.Solution: Let the components of limited size are 1, 2 and 3. Now the GSAB space is
where 3 is observed in the both way.Solution: Let the components of limited size are 1, 2 and 3. Now the GSAB space is 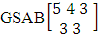 = (b11 , b22 , b33 ), (b11 , b23 , b32 ), (b12 , b21 , b33), (b12 , b23 , b31 ), (b13 , b21 , b32 ), ( b13 , b22 , b31 ).Definition 1.54 GASB space: A GASB space is a set of all possible outcomes of the GASB experiment
= (b11 , b22 , b33 ), (b11 , b23 , b32 ), (b12 , b21 , b33), (b12 , b23 , b31 ), (b13 , b21 , b32 ), ( b13 , b22 , b31 ).Definition 1.54 GASB space: A GASB space is a set of all possible outcomes of the GASB experiment  . It is denoted by
. It is denoted by 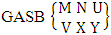 (read GASB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.42: Find the GASB space against the GASB experiment
(read GASB space of M sided N dice taken V at a time where X, Y are observed for U). Example 1.42: Find the GASB space against the GASB experiment 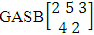 where 1 is observed in the second way.Solution: Let the components of limited size are 1, 2 and 3. Now the GASB space is
where 1 is observed in the second way.Solution: Let the components of limited size are 1, 2 and 3. Now the GASB space is 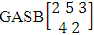 = (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12 , b13 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b13 , b14 , b25 ), (b12 , b13 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b13 , b24 , b15 ), (b12 , b13 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b13 , b24 , b25 ), (b12 , b13 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b23 , b14 , b15 ), (b12 , b23 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b23 , b14 , b25 ), (b12 , b23 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b23 , b24 , b15 ), (b12 , b23 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b11 , b23 , b24 , b25 ), (b12 , b23 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b13 , b14 , b15 ), (b22 , b13 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b13 , b14 , b25 ), (b22 , b13 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b13 , b24 , b15 ), (b22 , b13 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b13 , b24 , b25 ), (b22 , b13 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b23 , b14 , b15 ), (b22 , b23 , b14 , b15 ), (b21 , b22 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b22 , b23 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b23 , b24 , b15 ), (b22 , b23 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b21 , b23 , b24 , b25 ), (b22 , b23 , b24 , b25 ).The following discusses three kinds of GB spaces i.e., first way GB space, second way GB space and both way GB space with their different forms.Definition 1.55 First way GB space: A first way GB space is a set of all possible outcomes of the first way GB experiment
= (b11 , b12 , b14 , b15 ), (b11 , b13 , b14 , b15 ), (b12 , b13 , b14 , b15 ), (b11 , b12 , b14 , b25 ), (b11 , b13 , b14 , b25 ), (b12 , b13 , b14 , b25 ), (b11 , b12 , b24 , b15 ), (b11 , b13 , b24 , b15 ), (b12 , b13 , b24 , b15 ), (b11 , b12 , b24 , b25 ), (b11 , b13 , b24 , b25 ), (b12 , b13 , b24 , b25 ), (b11 , b22 , b14 , b15 ), (b11 , b23 , b14 , b15 ), (b12 , b23 , b14 , b15 ), (b11 , b22 , b14 , b25 ), (b11 , b23 , b14 , b25 ), (b12 , b23 , b14 , b25 ), (b11 , b22 , b24 , b15 ), (b11 , b23 , b24 , b15 ), (b12 , b23 , b24 , b15 ), (b11 , b22 , b24 , b25 ), (b11 , b23 , b24 , b25 ), (b12 , b23 , b24 , b25 ), (b21 , b12 , b14 , b15 ), (b21 , b13 , b14 , b15 ), (b22 , b13 , b14 , b15 ), (b21 , b12 , b14 , b25 ), (b21 , b13 , b14 , b25 ), (b22 , b13 , b14 , b25 ), (b21 , b12 , b24 , b15 ), (b21 , b13 , b24 , b15 ), (b22 , b13 , b24 , b15 ), (b21 , b12 , b24 , b25 ), (b21 , b13 , b24 , b25 ), (b22 , b13 , b24 , b25 ), (b21 , b22 , b14 , b15 ), (b21 , b23 , b14 , b15 ), (b22 , b23 , b14 , b15 ), (b21 , b22 , b14 , b15 ), (b21 , b23 , b14 , b25 ), (b22 , b23 , b14 , b25 ), (b21 , b22 , b24 , b15 ), (b21 , b23 , b24 , b15 ), (b22 , b23 , b24 , b15 ), (b21 , b22 , b24 , b25 ), (b21 , b23 , b24 , b25 ), (b22 , b23 , b24 , b25 ).The following discusses three kinds of GB spaces i.e., first way GB space, second way GB space and both way GB space with their different forms.Definition 1.55 First way GB space: A first way GB space is a set of all possible outcomes of the first way GB experiment 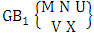 . It is denoted by
. It is denoted by 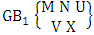 (read first way GB space of M sided N dice taken V at a time where X is observed for U).Example 1.43: Find the first way GB space against the first way GB experiment
(read first way GB space of M sided N dice taken V at a time where X is observed for U).Example 1.43: Find the first way GB space against the first way GB experiment 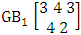 .Solution: Suppose the desired GB space chosen first way arranged and second way selected then the first way GB space
.Solution: Suppose the desired GB space chosen first way arranged and second way selected then the first way GB space 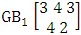 worked out in example 1.38. Definition 1.56 Second way GB space: A second way GB space is a set of all possible outcomes of the second way GB experiment
worked out in example 1.38. Definition 1.56 Second way GB space: A second way GB space is a set of all possible outcomes of the second way GB experiment 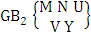 . It is denoted by
. It is denoted by 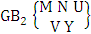 (read second way GB space of M sided N dice taken V at a time where Y is observed for U).Example 1.44: Find the second way GB space against the second way GB experiment
(read second way GB space of M sided N dice taken V at a time where Y is observed for U).Example 1.44: Find the second way GB space against the second way GB experiment 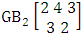 .Solution: Suppose the desired GB space chosen both way arranged then the second way GB space
.Solution: Suppose the desired GB space chosen both way arranged then the second way GB space 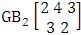 worked out in example 1.40. Definition 1.57 Both way GB space: A both way GB space is a set of all possible outcomes of the both way GB experiment
worked out in example 1.40. Definition 1.57 Both way GB space: A both way GB space is a set of all possible outcomes of the both way GB experiment 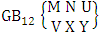 . It is denoted by
. It is denoted by 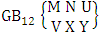 (read both way GB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.45: Find the both way GB space against the both way GB experiment
(read both way GB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.45: Find the both way GB space against the both way GB experiment 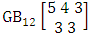 .Solution: Suppose the desired GB space chosen first way selected and second way arranged then the both way GB space
.Solution: Suppose the desired GB space chosen first way selected and second way arranged then the both way GB space 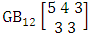 worked out in example 1.41.Definition 1.3.58 First way GSB space: A first way GSB space is a set of all possible outcomes of the first way GSB experiment
worked out in example 1.41.Definition 1.3.58 First way GSB space: A first way GSB space is a set of all possible outcomes of the first way GSB experiment 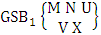 . It is denoted by
. It is denoted by 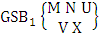 (read first way GSB space of M sided N dice taken V at a time where X is observed for U).Example 1.46: Find the first way GSB space against the first way GSB experiment
(read first way GSB space of M sided N dice taken V at a time where X is observed for U).Example 1.46: Find the first way GSB space against the first way GSB experiment 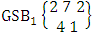 .Solution: Let the components of limited size are 1 and 2. Now the first way GSB space is
.Solution: Let the components of limited size are 1 and 2. Now the first way GSB space is 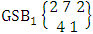 = (b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b12 , b15 , b16 ), (b11 , b12 , b15 , b17 ), (b11 , b12 , b16 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16 ), (b11 , b13 , b14 , b17 ), (b11 , b13 , b15 , b16 ), (b11 , b13 , b15 , b17 ), (b11 , b13 , b16 , b17 ), (b11 , b14 , b15 , b16 ), (b11 , b14 , b15 , b17 ), (b11 , b14 , b16 , b17 ), (b11 , b15 , b16 , b17 ), ( b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b12 , b13 , b15 , b16 ), (b12 , b13 , b15 , b17 ), (b12 , b13 , b16 , b17 ), (b12 , b14 , b15 , b16 ), (b12 , b14 , b15 , b17 ), (b12 , b14 , b16 , b17 ), (b12 , b15 , b16 , b17 ), (b13 , b14 , b15 , b16 ), ( b13 , b14 , b15 , b17 ), (b13 , b14 , b16 , b17 ), (b13 , b15 , b16 , b17 ), (b14 , b15 , b16 , b17 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b22 , b25 , b26 ), (b21 , b22 , b25 , b27 ), (b21 , b22 , b26 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b21 , b23 , b25 , b26 ), (b21 , b23 , b25 , b27 ), (b21 , b23 , b26 , b27 ), (b21 , b24 , b25 , b26 ), (b21 , b24 , b25 , b27 ), (b21 , b24 , b26 , b27 ), (b21 , b25 , b26 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b25 , b26), (b22 , b23 , b25 , b27 ), (b22 , b23 , b24 , b27 ), (b22 , b23 , b26 , b27 ), (b22 , b24 , b25 , b26 ), (b22 , b24 , b25 , b27 ), (b22 , b24 , b26 , b27 ), (b22 , b25 , b26 , b27 ), (b23 , b24 , b25 , b26 ), (b23 , b24 , b25 , b27 ), (b23 , b24 , b26 , b27 ), (b23 , b25 , b26 , b27 ), (b24 , b25 , b26 , b27 ).Definition 1.59 Second way GSB space: A second way GSB space is a set of all possible outcomes of the second way GSB experiment
= (b11 , b12 , b13 , b14 ), (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b12 , b15 , b16 ), (b11 , b12 , b15 , b17 ), (b11 , b12 , b16 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16 ), (b11 , b13 , b14 , b17 ), (b11 , b13 , b15 , b16 ), (b11 , b13 , b15 , b17 ), (b11 , b13 , b16 , b17 ), (b11 , b14 , b15 , b16 ), (b11 , b14 , b15 , b17 ), (b11 , b14 , b16 , b17 ), (b11 , b15 , b16 , b17 ), ( b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b12 , b13 , b15 , b16 ), (b12 , b13 , b15 , b17 ), (b12 , b13 , b16 , b17 ), (b12 , b14 , b15 , b16 ), (b12 , b14 , b15 , b17 ), (b12 , b14 , b16 , b17 ), (b12 , b15 , b16 , b17 ), (b13 , b14 , b15 , b16 ), ( b13 , b14 , b15 , b17 ), (b13 , b14 , b16 , b17 ), (b13 , b15 , b16 , b17 ), (b14 , b15 , b16 , b17 ), (b21 , b22 , b23 , b24 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b22 , b25 , b26 ), (b21 , b22 , b25 , b27 ), (b21 , b22 , b26 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b21 , b23 , b25 , b26 ), (b21 , b23 , b25 , b27 ), (b21 , b23 , b26 , b27 ), (b21 , b24 , b25 , b26 ), (b21 , b24 , b25 , b27 ), (b21 , b24 , b26 , b27 ), (b21 , b25 , b26 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b25 , b26), (b22 , b23 , b25 , b27 ), (b22 , b23 , b24 , b27 ), (b22 , b23 , b26 , b27 ), (b22 , b24 , b25 , b26 ), (b22 , b24 , b25 , b27 ), (b22 , b24 , b26 , b27 ), (b22 , b25 , b26 , b27 ), (b23 , b24 , b25 , b26 ), (b23 , b24 , b25 , b27 ), (b23 , b24 , b26 , b27 ), (b23 , b25 , b26 , b27 ), (b24 , b25 , b26 , b27 ).Definition 1.59 Second way GSB space: A second way GSB space is a set of all possible outcomes of the second way GSB experiment 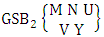 . It is denoted by
. It is denoted by 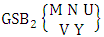 (read second way GSB space of M sided N dice taken V at a time where Y is observed for U).Example 1.47: Find the second way GSB space against the second way GSB experiment
(read second way GSB space of M sided N dice taken V at a time where Y is observed for U).Example 1.47: Find the second way GSB space against the second way GSB experiment  .Solution: The solution is worked out in example 1.39.Definition 1.60 Both way GSB space: A both way GSB space is a set of all possible outcomes of the both way GSB experiment
.Solution: The solution is worked out in example 1.39.Definition 1.60 Both way GSB space: A both way GSB space is a set of all possible outcomes of the both way GSB experiment 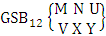 . It is denoted by
. It is denoted by 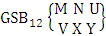 (read both way GSB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.48: Find the both way GSB space against the both way GSB experiment
(read both way GSB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.48: Find the both way GSB space against the both way GSB experiment 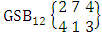 .Solution: Let the components of limited size are 1, 2, 3 and 4 and 1, 3 observed in the both way i.e., 1 in first way and 3 in second way. Hence the desired space is
.Solution: Let the components of limited size are 1, 2, 3 and 4 and 1, 3 observed in the both way i.e., 1 in first way and 3 in second way. Hence the desired space is 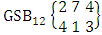 = (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16 ), (b11 , b13 , b14 , b17 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b24 , b27 ).Definition 1.61 First way GAB space: A first way GAB space is a set of all possible outcomes of the first way GAB experiment
= (b11 , b12 , b13 , b15 ), (b11 , b12 , b13 , b16 ), (b11 , b12 , b13 , b17 ), (b11 , b12 , b14 , b15 ), (b11 , b12 , b14 , b16 ), (b11 , b12 , b14 , b17 ), (b11 , b13 , b14 , b15 ), (b11 , b13 , b14 , b16 ), (b11 , b13 , b14 , b17 ), (b12 , b13 , b14 , b15 ), (b12 , b13 , b14 , b16 ), (b12 , b13 , b14 , b17 ), (b21 , b22 , b23 , b25 ), (b21 , b22 , b23 , b26 ), (b21 , b22 , b23 , b27 ), (b21 , b22 , b24 , b25 ), (b21 , b22 , b24 , b26 ), (b21 , b22 , b24 , b27 ), (b21 , b23 , b24 , b25 ), (b21 , b23 , b24 , b26 ), (b21 , b23 , b24 , b27 ), (b22 , b23 , b24 , b25 ), (b22 , b23 , b24 , b26 ), (b22 , b23 , b24 , b27 ).Definition 1.61 First way GAB space: A first way GAB space is a set of all possible outcomes of the first way GAB experiment 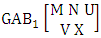 . It is denoted by
. It is denoted by 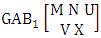 (read first way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.49: Find the first way GAB space against the first way GAB experiment
(read first way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.49: Find the first way GAB space against the first way GAB experiment 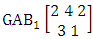 .Solution: Let the components of limited size are 1 and 2 and the desired space is
.Solution: Let the components of limited size are 1 and 2 and the desired space is 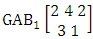 = (b11 , b12 , b13 ), (b11 , b12 , b14 ), (b11 , b13 , b12 ), (b11 , b13 , b14 ), (b11 ,b14, b12 ), (b11, b14, b13 ), (b12 , b11 , b13 ), (b12 , b11, b14 ), (b12 , b13, b11 ), (b12 , b13 , b14 ), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b13 , b11 , b12), (b13 , b11 , b14 ), (b13 , b12 , b11 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b21 , b22 , b23 ), (b21 , b22 , b24 ), (b21 , b23 , b22), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b22 , b21 , b23 ), (b22 , b21 , b24 ), (b22 , b23 , b21 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b23 , b21 , b22 ), (b23 , b21 , b24 ), (b23 , b22 , b21), (b23 , b22 , b24 ), (b23 , b24, b21 ), (b23 , b24 , b22 ), (b24 , b21 , b22 ), (b24 , b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.62 Second way GAB space: A second way GAB space is a set of all possible outcomes of the second way GAB experiment
= (b11 , b12 , b13 ), (b11 , b12 , b14 ), (b11 , b13 , b12 ), (b11 , b13 , b14 ), (b11 ,b14, b12 ), (b11, b14, b13 ), (b12 , b11 , b13 ), (b12 , b11, b14 ), (b12 , b13, b11 ), (b12 , b13 , b14 ), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b13 , b11 , b12), (b13 , b11 , b14 ), (b13 , b12 , b11 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b21 , b22 , b23 ), (b21 , b22 , b24 ), (b21 , b23 , b22), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b22 , b21 , b23 ), (b22 , b21 , b24 ), (b22 , b23 , b21 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b23 , b21 , b22 ), (b23 , b21 , b24 ), (b23 , b22 , b21), (b23 , b22 , b24 ), (b23 , b24, b21 ), (b23 , b24 , b22 ), (b24 , b21 , b22 ), (b24 , b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.62 Second way GAB space: A second way GAB space is a set of all possible outcomes of the second way GAB experiment 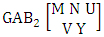 . It is denoted by
. It is denoted by 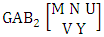 (read second way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.50: Find the second way GAB space against the second way GAB experiment
(read second way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.50: Find the second way GAB space against the second way GAB experiment 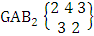 .Solution: The solution is worked out in example 1.40.Definition 1.63 Both way GAB space: A both way GAB space is a set of all possible outcomes of the both way GAB experiment
.Solution: The solution is worked out in example 1.40.Definition 1.63 Both way GAB space: A both way GAB space is a set of all possible outcomes of the both way GAB experiment 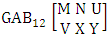 . It is denoted by
. It is denoted by 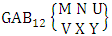 (read both way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.51: Find the both way GAB space against the both way GAB experiment
(read both way GAB space of M sided N dice taken V at a time where X is observed for U).Example 1.51: Find the both way GAB space against the both way GAB experiment 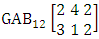 .Solution: Let the components of limited size are 1 and 2 and 1, 2 observed in both way i.e., 1 in first way and 2 in second way. Hence the desired space is
.Solution: Let the components of limited size are 1 and 2 and 1, 2 observed in both way i.e., 1 in first way and 2 in second way. Hence the desired space is 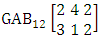 = (b11 , b12 , b14 ), (b11 , b13 , b14 ), (b11 , b14 , b12 ), (b11 , b14 , b13 ), (b12 , b11 , b14 ), (b12 , b13 , b14), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b13 , b11 , b14 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b21 , b22 , b24 ), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b22 , b21 , b24 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b23 , b21 , b24 ), (b23 , b22 , b24 ), (b23 , b24 , b21 ), (b23 , b24 , b22 ), (b24 , b21 , b22 ), (b24 ,, b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.64 First way GSAB space: A first way GSAB space is a set of all possible outcomes of the first way GSAB experiment
= (b11 , b12 , b14 ), (b11 , b13 , b14 ), (b11 , b14 , b12 ), (b11 , b14 , b13 ), (b12 , b11 , b14 ), (b12 , b13 , b14), (b12 , b14 , b11 ), (b12 , b14 , b13 ), (b13 , b11 , b14 ), (b13 , b12 , b14 ), (b13 , b14 , b11 ), (b13 , b14 , b12 ), (b14 , b11 , b12 ), (b14 , b11 , b13 ), (b14 , b12 , b11 ), (b14 , b12 , b13 ), (b14 , b13 , b11 ), (b14 , b13 , b12 ), (b21 , b22 , b24 ), (b21 , b23 , b24 ), (b21 , b24 , b22 ), (b21 , b24 , b23 ), (b22 , b21 , b24 ), (b22 , b23 , b24 ), (b22 , b24 , b21 ), (b22 , b24 , b23 ), (b23 , b21 , b24 ), (b23 , b22 , b24 ), (b23 , b24 , b21 ), (b23 , b24 , b22 ), (b24 , b21 , b22 ), (b24 ,, b21 , b23 ), (b24 , b22 , b21 ), (b24 , b22 , b23 ), (b24 , b23 , b21 ), (b24 , b23 , b22 ).Definition 1.64 First way GSAB space: A first way GSAB space is a set of all possible outcomes of the first way GSAB experiment 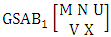 . It is denoted by
. It is denoted by 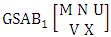 (read first way GSAB space of M sided N dice taken V at a time where X is observed for U).Example 1.52: Find the first way GSAB space against the first way GSAB experiment
(read first way GSAB space of M sided N dice taken V at a time where X is observed for U).Example 1.52: Find the first way GSAB space against the first way GSAB experiment 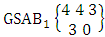 .Solution: Let the components of limited size are 1, 2 and 3 and 0 observed in the first way. So the desired space is
.Solution: Let the components of limited size are 1, 2 and 3 and 0 observed in the first way. So the desired space is 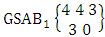 = (b41 , b42, b43 ), (b41 , b42 , b44 ), (b41 , b43 , b42 ), (b41 , b43 , b44 ), (b41 , b44 , b42 ), (b41 , b44 , b43 ), (b42 , b41 , b43 ), (b42 , b41 , b44 ), (b42 , b43 , b41), (b42 , b43 , b44 ), (b42 , b44 , b41 ), (b42 , b44 , b43 ), (b43 , b41 , b42 ), (b43 , b41 , b44 ), (b43 , b42 , b41), (b43 , b42 , b44 ), (b43 , b44 , b41 ), (b43 , b44 , b42 ), (b44 , b41 , b42 ), (b44 , b41 , b43 ), (b44 , b42 , b41 ), (b44 , b42 , b43 ), (b44 , b43 , b41 ), (b44 , b43 , b42 ).Definition 1.65 Second way GSAB space: A second way GSAB space is a set of all possible outcomes of the second way GSAB experiment
= (b41 , b42, b43 ), (b41 , b42 , b44 ), (b41 , b43 , b42 ), (b41 , b43 , b44 ), (b41 , b44 , b42 ), (b41 , b44 , b43 ), (b42 , b41 , b43 ), (b42 , b41 , b44 ), (b42 , b43 , b41), (b42 , b43 , b44 ), (b42 , b44 , b41 ), (b42 , b44 , b43 ), (b43 , b41 , b42 ), (b43 , b41 , b44 ), (b43 , b42 , b41), (b43 , b42 , b44 ), (b43 , b44 , b41 ), (b43 , b44 , b42 ), (b44 , b41 , b42 ), (b44 , b41 , b43 ), (b44 , b42 , b41 ), (b44 , b42 , b43 ), (b44 , b43 , b41 ), (b44 , b43 , b42 ).Definition 1.65 Second way GSAB space: A second way GSAB space is a set of all possible outcomes of the second way GSAB experiment 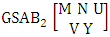 . It is denoted by
. It is denoted by 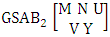 (read second way GSAB space of M sided N dice taken V at a time where Y is observed for U).Example 1.53: Find the second way GSAB space against the second way GSAB experiment
(read second way GSAB space of M sided N dice taken V at a time where Y is observed for U).Example 1.53: Find the second way GSAB space against the second way GSAB experiment 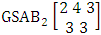 .Solution: Let the components of limited size are 1, 2 and 3 and 3 observed in the second way. So the desired space is
.Solution: Let the components of limited size are 1, 2 and 3 and 3 observed in the second way. So the desired space is 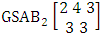 = (b11 , b12 , b13 ), (b11 , b13 , b12 ), (b12 , b11 , b13 ), (b12 , b13 , b11 ), (b13 , b11 , b12 ), (b13 , b12 , b11 ), (b11 , b12 , b23 ), (b11 , b13 , b22 ), (b12 , b11 , b23 ), (b12 , b13 , b21 ), (b13 , b11 , b22 ), (b13 , b12 , b21 ), (b11 , b22 , b23), (b11 , b23 , b22 ), (b12 , b21 , b23 ), (b12 , b23 , b21 ), (b13 , b21 , b22 ), (b13 , b22 , b21 ), (b21 , b22 , b23 ), (b21 , b23 , b22 ), (b22 , b21 , b23 ), (b22 , b23 , b21 ), (b23 , b21 , b22 ), (b23 , b22 , b21 ).Definition 1.66 Both way GSAB space: A both way GSAB space is a set of all possible outcomes of the both way GSAB experiment
= (b11 , b12 , b13 ), (b11 , b13 , b12 ), (b12 , b11 , b13 ), (b12 , b13 , b11 ), (b13 , b11 , b12 ), (b13 , b12 , b11 ), (b11 , b12 , b23 ), (b11 , b13 , b22 ), (b12 , b11 , b23 ), (b12 , b13 , b21 ), (b13 , b11 , b22 ), (b13 , b12 , b21 ), (b11 , b22 , b23), (b11 , b23 , b22 ), (b12 , b21 , b23 ), (b12 , b23 , b21 ), (b13 , b21 , b22 ), (b13 , b22 , b21 ), (b21 , b22 , b23 ), (b21 , b23 , b22 ), (b22 , b21 , b23 ), (b22 , b23 , b21 ), (b23 , b21 , b22 ), (b23 , b22 , b21 ).Definition 1.66 Both way GSAB space: A both way GSAB space is a set of all possible outcomes of the both way GSAB experiment 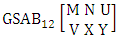 . It is denoted by
. It is denoted by 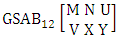 (read both way GSAB space of M sided N dice taken V at a time where X , Y are observed for U).Example 1.54: Find the both way GSAB space against the both way GSAB experiment
(read both way GSAB space of M sided N dice taken V at a time where X , Y are observed for U).Example 1.54: Find the both way GSAB space against the both way GSAB experiment 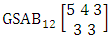 .Solution: The solution is worked out in example 1.41.Definition 1.67 First way GASB space: A first way GASB space is a set of all possible outcomes of the first way GASB experiment
.Solution: The solution is worked out in example 1.41.Definition 1.67 First way GASB space: A first way GASB space is a set of all possible outcomes of the first way GASB experiment 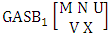 . It is denoted by
. It is denoted by 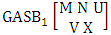 (read first way GASB space of M sided N dice taken V at a time where X is observed for U).Example 1.55: Find the first way GASB space against the first way GASB experiment
(read first way GASB space of M sided N dice taken V at a time where X is observed for U).Example 1.55: Find the first way GASB space against the first way GASB experiment 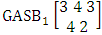 .Solution: The solution is worked out in example 1.38.Definition 1.68 Second way GASB space: A second way GASB space is a set of all possible outcomes of the second way GASB experiment
.Solution: The solution is worked out in example 1.38.Definition 1.68 Second way GASB space: A second way GASB space is a set of all possible outcomes of the second way GASB experiment 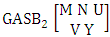 . It is denoted by
. It is denoted by 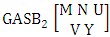 (read second way GASB space of M sided N dice taken V at a time where Y is observed for U).Example 1.56: Find the both way GASB space against the second way GASB experiment
(read second way GASB space of M sided N dice taken V at a time where Y is observed for U).Example 1.56: Find the both way GASB space against the second way GASB experiment 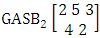 .Solution: The solution is worked out in example 1.42.Definition 1.69 Both way GASB space: A both way GASB space is a set of all possible outcomes of the both way GASB experiment
.Solution: The solution is worked out in example 1.42.Definition 1.69 Both way GASB space: A both way GASB space is a set of all possible outcomes of the both way GASB experiment 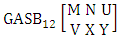 . It is denoted by
. It is denoted by 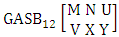 (read both way GASB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.57: Find the both way GASB space against the both way GASB experiment
(read both way GASB space of M sided N dice taken V at a time where X, Y are observed for U).Example 1.57: Find the both way GASB space against the both way GASB experiment 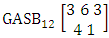 .Solution: Let the components of limited size are 1, 2 and 3 and 1 observed in the both way. Hence the desired space is
.Solution: Let the components of limited size are 1, 2 and 3 and 1 observed in the both way. Hence the desired space is 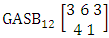 = (b11 , b14 , b15 , b16 ), (b12 , b14 , b15 , b16 ), (b13 , b14 , b15 , b16 ), (b21 , b24 , b25 , b26 ), (b22 , b14 , b25 , b26 ), (b23 , b24 , b25 , b26 ), (b31 , b34 , b35 , b36 ), (b32 , b34 , b35 , b36 ), (b33 , b34 , b35 , b36 ).
= (b11 , b14 , b15 , b16 ), (b12 , b14 , b15 , b16 ), (b13 , b14 , b15 , b16 ), (b21 , b24 , b25 , b26 ), (b22 , b14 , b25 , b26 ), (b23 , b24 , b25 , b26 ), (b31 , b34 , b35 , b36 ), (b32 , b34 , b35 , b36 ), (b33 , b34 , b35 , b36 ).3. Conclusions
- In this paper we found EB members, IB members, CB members and GB members of an experiment “M sided N dice taken V at a time”. Beside this we get combinations, permutations, formations and homogenations as B members. The paper will helps to find out the Biswas theorem with related theorems and Biswas distribution with related distributions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML