-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2018; 8(2): 59-64
doi:10.5923/j.statistics.20180802.04

Bayesian Estimation of Proportion of Women Engaged in Sudan Agricultural Development: An R-WinBUGS Application
Siraj Osman Omer , Mai Ibrahim Eljack , Zahia Sayed
Experimental Design and Analysis Unit, Agricultural Research Corporation, Wad Medani, Sudan
Correspondence to: Siraj Osman Omer , Experimental Design and Analysis Unit, Agricultural Research Corporation, Wad Medani, Sudan.
| Email: |  |
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

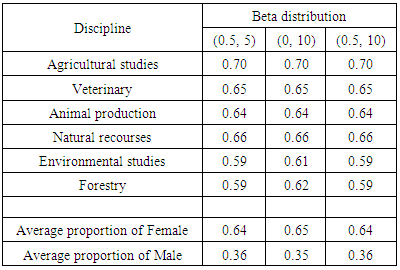
The objective of this paper is to estimate the proportion of women engaged in Sudan agricultural development. The study was used classical and Bayesian approaches where the best of the three priors were chosen for posterior estimation proportion. The agricultural studies graduate’s data from governmental universities in Sudan for 2010-2011 were used. R2WinBUGS software for Bayesian inference on Binomial parameters can be used. The results showed that there was a significant difference (P<0.01) between classical estimation of female (67%) points compared that with male students (33%). The Bayesian estimate of the proportion of women was found as 64% when the prior distribution was beta (0.5, 0.5) and 65% for beta (0, 10). Bayesian approach for statistical inference in this study is useful and acceptable in gender studies. Bayesian estimation has been outlined for an estimation of the proportion of women engaged in Sudan agricultural development.
Keywords: Bayesian estimation, Binomial distribution, R-language, WINBUGS
Cite this paper: Siraj Osman Omer , Mai Ibrahim Eljack , Zahia Sayed , Bayesian Estimation of Proportion of Women Engaged in Sudan Agricultural Development: An R-WinBUGS Application, International Journal of Statistics and Applications, Vol. 8 No. 2, 2018, pp. 59-64. doi: 10.5923/j.statistics.20180802.04.
Article Outline
1. Introduction
- Women play an indispensable role in farming and in improving the quality of life in rural areas, therefore, women are increasingly more likely to engage in agricultural fields compared to males [1]. The successful application of Bayesian data analysis has appeared in many different fields, including biological, environmental and social sciences, health sciences, business, computer science [2]. In Bayesian statistics, all uncertainties and all information are incorporated through the use of probability distributions, and all conclusions obey the laws of probability theory [3]. Many applications of the Bayesian method involve estimation of an unobservable parameter [4]. Bayesian approach demonstrates estimation by providing a natural and coherent approach for representing and manipulating all forms of uncertainty in modeling [5]. The probability mass function for a binomial model tells us how the probabilities of the different possible outcomes of an experiment vary as functions of fixed values of the parameters [6]. In the case of gender issue we might have data from prior experiments with similar populations which suggest that some values of the estimation probability are probably than others, because information can be incorporated into the analysis reason in a Bayesian inferences and decisions, because the Bayesian paradigm is the most acceptable approach, so far invented for quantifying all relevant sources of uncertainty in complicated problems and making choices in the face of such uncertainty [7]. Use of Markov Chain Monte Carlo (MCMC) methods, including WinBUGS for Bayesian inference requires knowledge and skill beyond statistical modeling [8]. In Binomial model, the choice of initial values may affect convergence substantially [9]. Literature containing recommendations on how to deal with these issues in MCMC use includes Brooks (1998), and Gilks, Richardson, and Spiegelhalter [10] sampling from the posterior Bayesian inference is usually presented as a method for determining how scientific belief should be modified by data [12]. R2WinBUGS package in R will be implemented, because it offers a versatile approach for making MCMC computations within WinBUGS and returning them to R [13]. The feature of R2WinBUGS software uses a text file containing the data model with parameters, and information on the parameters’ a priori distribution [14]. In Binomial probability, Bayesian inference can be used to estimate the proportion (p) of female and male. Bayesian approach estimate is necessary to candidate the best prior for posterior probability distribution [11]. estimate of proportion (p) [15]. In this study a case of the simple binomial model can be computed the posterior summaries such as mean, mode, standard deviation and percentile intervals using WinBUGS software model development. The objective of this paper is to estimate the proportion of women engaged in Sudan agricultural development. In this study a Bayesian approach considering the using uniform prior.
2. Methodologies
2.1. Dataset
- Data were obtained from the website http://www.mohe.gov.sd/ of the Ministry of Higher Education and Scientific Research on data agricultural studies graduates from governmental universities in Sudan for 2010-2011. The agricultural students graduate take as random sample from different agricultural colleges with different disciplines, despite starting with priors having quite different shapes in binomial model of the population contains a fixed number of departments/ colleges (n) in assumed that every student has the same probability of engaged in Sudan agricultural development, so the in binomial model, Bayesian posterior density is a true probability density which can be used to make direct probability statements about a parameter.
2.2. Statistical Methods
2.2.1. Binomial Distribution
- In this study the conditional distributions of observed data say Y and let parameters
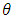 to be the probability of success in a total of n independent trials of binomial distribution (n, θ). The conditional probability function for Y given
to be the probability of success in a total of n independent trials of binomial distribution (n, θ). The conditional probability function for Y given 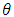 is given by
is given by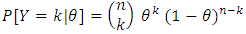 | (1) |
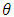 is held as fixed at the probability distribution of Y over its possible values k=1…n.
is held as fixed at the probability distribution of Y over its possible values k=1…n. 2.2.2. Binomial Distribution in WinBUGS
- WinBUGS is a software package that uses Markov chain Monte Carlo (MCMC) methods to fit Bayesian statistical models, has facilitated Bayesian analysis in a wide variety of application areas [11]. R2WinBUGS is an R package for executing WinBUGS from R [16] Walters (1985) used the uniform prior and its implied posterior distribution in constructing a confidence interval for a binomial parameter (in Bayesian terminology, a credible region"). Also Diaconis and Freedman (1990) investigated the degree to which posterior distributions put relatively greater mass close to the sample proportion p as n increases. Bayesian Inference for a prior distribution for a proportion is given as fallow
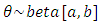 | (2) |
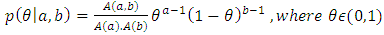 | (3) |
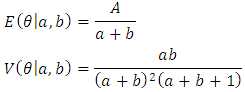 | (4) |
2.2.3. Prior Distribution
- Prior information in Bayesian analyses is represented by probability distributions for the parameters and uniform prior can be used of previous data on the impacts of gender issues in human development [19]. The uniform prior of Beta (2, 2) =U (0, 1) corresponds to having 2 prior experiments, one of which was a woman and the other man. Moreover, with Beta (0, 0) prior the posterior is not defending if the observed data happen to be either 0 or N under a Binomial such as (n;k) model. For single parameters, the Jffreys' prior is sometimes used, but for Multiparameter problems the results are more controversial, and a hierarchical modeling approach is more common. Uncertainty about parameter can be updated repeatedly when new data are available for taking a current posterior distribution as prior and compute new posterior distribution conditional on new data [20].
2.3. Bayesian Estimation of Binomial Proportion
- Bolstad (2004) has derived the Bayesian estimator of a binomial proportion for Bayesian estimation of binomial proportion where, a proportion of the population has some attribute will came from large population. In study a random sample from the population will be taken and let Y be the observed number of the population. The conditional distribution of the observation Y, the total number of successes in n trials given the parameter, is binomial (n, k). The conditional probability function or likelihood function for y given
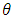 is given by
is given by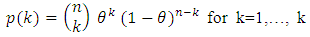 | (5) |
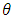 is assuming as a fixed, and looking at the probability distribution of y over its possible values. Therefore, relationship between
is assuming as a fixed, and looking at the probability distribution of y over its possible values. Therefore, relationship between 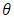 and k, can be holding k fixed parameters at the number of successes we observed. To use Bayes’ theorem, assuming g(
and k, can be holding k fixed parameters at the number of successes we observed. To use Bayes’ theorem, assuming g(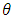 ) is prior distribution that gives our belief about the possible values of the parameter
) is prior distribution that gives our belief about the possible values of the parameter 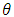 before taking the data. It is important to realize that the prior must not be constructed from the data. Bayes’ theorem is summarized by posterior is proportional to the prior times the likelihood.
before taking the data. It is important to realize that the prior must not be constructed from the data. Bayes’ theorem is summarized by posterior is proportional to the prior times the likelihood.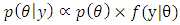 | (6) |
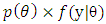 over the whole range. So, in general,
over the whole range. So, in general,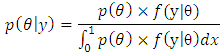 This requires integration. Depending on the prior
This requires integration. Depending on the prior 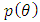 chosen, there may not necessarily be a closed form for the integral, so it may be necessary to the integration numerically. Suppose a beta(a,b) prior density is used for
chosen, there may not necessarily be a closed form for the integral, so it may be necessary to the integration numerically. Suppose a beta(a,b) prior density is used for 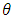 :
: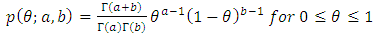 | (7) |
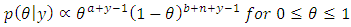 | (8) |
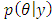 is the shape of the posterior as a function of
is the shape of the posterior as a function of 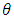 . beta distribution can recognized with parameters a′= a + y and b′= b + n −y. That is, we add the number of successes to a and number of failures to b:
. beta distribution can recognized with parameters a′= a + y and b′= b + n −y. That is, we add the number of successes to a and number of failures to b: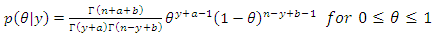 | (9) |
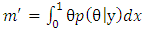 | (10) |
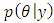 is beta(a′,b′) the posterior mean equals
is beta(a′,b′) the posterior mean equals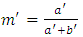 | (11) |
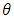 , can be estimated use the beta(1,1) prior (uniform prior).
, can be estimated use the beta(1,1) prior (uniform prior). 3. Results and Discussion
3.1. Case Study: Gender approaches in Agricultural Studies Graduates
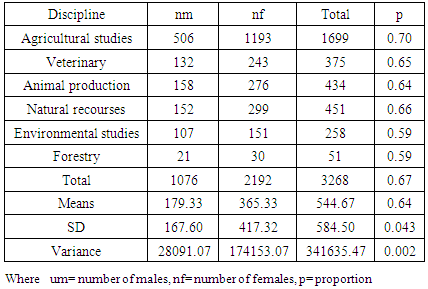
- Students graduated in agricultural studies, both male and female, need a job doing. In agricultural practices men are more willing to share decision-making with their wives, though working hardly in any situation or bad situation they generally still consider themselves household. The example view that, the number of females is more than male into all disciplines and gardening, it is important to note that these changes have occurred over a period as short as two or three years. Labor market needs an effective graduates depend upon qualification, experiences, availability and should be considered in the broader sense to include markets for inputs also required a good strategy, concepts of ‘participation’ and ‘gender’ has been a part of emancipator discourse and practices with increasingly visible as an issue in development. Gender has become increasingly visible as an issue in development and widely used in agricultural development, referring primarily to participation in projects or in the community [21]. Women participation needs be processed in inclusion and critical reflection encouraged by women participatory [22].
|
3.2. Selections of Priors
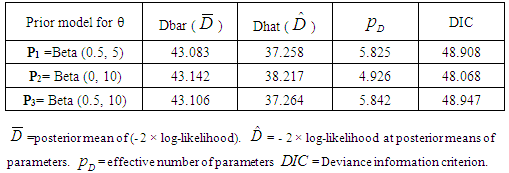
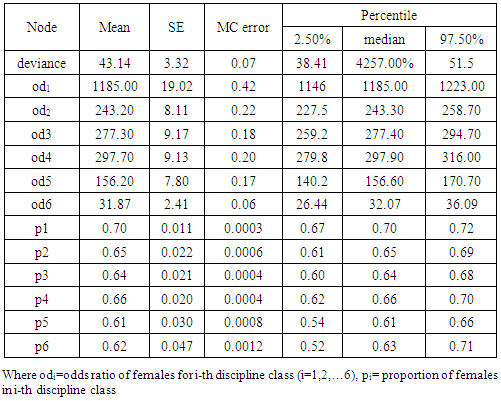
- The analysis components computed are presented along with the statistics using Bayesian approach in the Table 2, Table 3 and Table 4. The choices of priors for Bayesian analysis were made from the statistics given in Table 1. The values of DIC and pD are reasonably close to each other for the three priors sets P1, P2 and P3 of beta distribution respectively. However, the prior setb P2 seems to have numerically lowest value of DIC (48.068). We took P2 for further estimation of the estimation of proportion of women.
|
|
4. Conclusions
- The paper view, a framework developed for Bayesian binomial model for gender issue. In this study the data were analyzed using three candidate beta models. Bayesian estimation has been outlined of the proportion of women engaged in Sudan agricultural development. R2WinBUGS software package and R-environmental have been used with Markov chain Monte Carlo (MCMC) methods to fit Bayesian statistical models, has facilitated Bayesian analysis in a wide variety of applications, Bayesian estimation of proportion to the Binomial model based on percentage value is very close to the frequentist approach. Bayesian approach provides information on precision (in term of standard deviation and credible interval) of proportion of parameters.
Appendixes
- WinBugs code for binomial distribution
 WinBugs code for Bayesian binomial data analysis
WinBugs code for Bayesian binomial data analysis
References
| [1] | Raney, T., Anríquez, G., Croppenstedt, A., Gerosa, S., Lowder, S., Matuscke, I., Skoet, J. and Doss, C. FAO, ESA Working Paper No. 11-02, 2011. available at http://www.fao.org/publications/sofa/en/. |
| [2] | Gelman, A., Carlin, J.B., Stern, H.S. and Rubin, D.B. Bayesian Data Analysis. Second Edition.Chapman & Hall, Boca Raton, FL, 2004. |
| [3] | Koop. Bayesian Analysis, Computation and Communication Software. Journal of Applied Econometrics, vol.14, pp. 677-689. |
| [4] | Sevin., V. and Ergun, G., “Usage of different prior distribution Bayesian vector Autoregressive Models,” VoL.38, pp.85 – 93, 2009. |
| [5] | William, M. B., “Introduction to Bayesian Statistics,” ISBN, John Wiley & Sons, Inc, 2004. |
| [6] | DeCoursey W. J. Statistics and Probability for Engineering Applications With Microsoft® Excel, Library of Congress Cataloging-in-Publication Data, USA. ISBN: 978-0-7506-7618-2, 2003. |
| [7] | Draper, D., “Bayesian Statistical Analysis in Medical Research,” ROLE Steering Committee Meeting, New York NY, 2007. |
| [8] | Rahardja., D., Zhao, Y.D. and Zhang, H. Bayesian Credible Sets for a Binomial Proportion Based on One-Sample Binary Data Subject to One Type of Misclassi. Journal of Data Science, vol.10, pp. 51-59, 2012. |
| [9] | Stefano., C. and Spezzaferri, F., “A Bayesian Approach to Subset Analysis with Application to Binomial Count Data,” Translated: 2008-05-28 / SLB, 2005. |
| [10] | Spiegelhalter, D., Thomas, A., Best, N. and Gilks, W. BUGS 0.5: Bayesian inference Using Gibbs Sampling - Manual (version ii), Medical Research Council Biostatistics Unit, Cambridge, 1996. |
| [11] | Cowles., M.K., “Review of WinBUGS 1.4,” the American Statistician, Vol. 58, pp.4, 2014. |
| [12] | Goodman, S. N., “Toward Evidence-Based Medical Statistics: The Bayes Factor,” Ann Intern Med, vol.130, pp.1005-1013, 1999. |
| [13] | Ntzoufras, I. Bayesian Modeling Using WinBugs, First Edition, ISBN John Wiley & Sons, Inc, 2007. |
| [14] | Agresti, A. and Hitchcock. D., “Bayesian inference for categorical data analysis, Statistical Methods and Application (Journal of the Italian Statistical Society),” vol.14, pp.297-330, 2005. |
| [15] | Singh., M, Al-Yassin, A. and Omer, S. Bayesian Estimation of Genotypes Means, Precision and Genetic Gain due to Selection from Routinely Used Barley Trials. Crop Science, vol. 55, pp. 501–513, 2015. |
| [16] | Sturtz, S., Liggesy, U. and Gelman, A. R2OpenBUGS: A Package for Running WinBUGS from R. Journal of Statistical Software, vol. 12, pp. 1-16, 2005. |
| [17] | Lunn, D., Thomas, A., Best, N., Spiegelhalter, D. WinBUGS - a Bayesian modelling framework: concepts, structure, and extensibility. Statistics and Computing 10, 325–337, 2000. |
| [18] | Cowles, MK and Carlin, BP (1996) Markov chain Monte Carlo convergence diagnostics: a comparative review. Journal of the American Statistical Association, 91, 883–904. |
| [19] | Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Analysis 1, 515–533, 2009. |
| [20] | Jacobs., R., “Bayesian Statistics: Beta-Binomial Model,” Department of Brain & Cognitive Sciences, University of Rochester, Rochester, NY 14627, USA, 2008. |
| [21] | World Bank, FAO & IFAD. Gender in Agriculture Sourcebook. The World Bank, Washington D.C, 2009. |
| [22] | Supriya., A., “Gender and participation overview report,” Institute of Development Studies, ISBN 1 85864 385, 2001. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML