1. Introduction

There are certain circumstances in which the assumption of constant error variance or homoscedasticity in the linear model is not tenable. In testing for heteroscedasticity, there is need to have a relatively large samples in order to observe the problems of such errors and evaluate their behaviors. Researchers have observed that heteroscedasticity is usually found in cross sectional data. For example, one expects to observe greater variation in the profits of large firms than in those of small ones. The variance of profits might also depend on product diversification, research and development expenditure and industry characteristics and may therefore vary across firms of similar sizes. When analyzing family spending patterns, we find that there is greater variation in expenditure on certain commodity groups among high-income families than low ones due to the greater discretion allowed by higher income [Prais and Houthakker (1995)].

Goldfeld-Quandt (1965) observed that the power of their test depend on (a) the number of centrally omitted observations c and (b) the nature of the sample values of the variable used as the deflator. They also observed that, for very large valves of c, the power of their test is rather weak. Cook and Weisberg (1983), in their simulation study, investigated the χ² approximation of their test. They showed that their test is superior to Ancombe (1961) and Bickel (1978) because their χ² approximation of the sampling distribution is poor.

Kyung (2000) presented a paper on ‘Robustifying Glejser test of Heteroscedasticity’ where they proposed a simple modification to Glejser tests to make it more robust to disturbances with asymmetric density with flat tail. This problem had earlier been studied by Koenker and Bassett (1982) and Newey and Powell (1987). The later in particular focused their attention on the test proposed by Glejser (1969) which test whether the regression of the absolute values of residuals are correlated with some other variables. Newey and Powell (1987) presented a more elaborate test which is more powerful than the squared residual based test. Glejser test revisited by Machhado and Silva (2000) showed that the proposed test statistics are asymptotically valid even when the disturbances are not symmetrically distributed.

Xu (2006) presented new nonparametric tests for heteroscedasticity in nonlinear and nonparametric regression models. Monte Carlo simulations showed that, when the parametric tests misspecify the form of heteroscedasticity, the non parametric tests have much higher power against heteroscedasticity than the parametric tests. Thus, the non parametric tests are most useful when the form of heteroscedasticity cannot be specified with certainty or when the form is too complicated to be specified parametrically.

2. Methodology

The Nonlinear Models Investigated

1. The Cobb-Douglass production function, developed by Charles Cobb and Paul Douglass (1928) is a function showing the relationship between the output and the combination of factors, or inputs, used to obtain it. It is of the form:

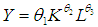(2.1)

The Cobb-Douglass Production Function with multiplicative error term can be represented as

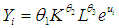(2.2)

where

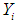is a dependent variable, 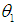is the intercept, 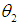and 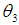are the regression coefficients, K and L a re independent variables and 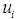is the error term.

The model in (2.2) can be transformed to linear model by taking the natural logarithms of both sides of the equation to obtain a regression model of the following form:

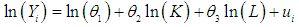(2.3)

2. The Exponential Production Function can be expressed in the form:

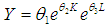(2.4)

The Exponential Production Function with multiplicative error term can be expressed as

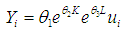(2.5)

where

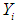is a dependent variable, 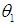is the intercept , 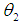and are the regression coefficients, K and L are independent variables and 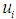is the error term.

By taking the natural logarithms of both sides of (2.5), we have

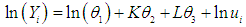(2.6)

3. Simulation

i. A sample infected with heteroscedasticity using uniform distribution to generate data for Capital (K), Labour (L) and Output (Y). The study used fixed values for 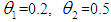and 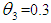for the two models.

ii. The set of parameter estimates obtained were used to compute the residuals which represented the dependent variable for the auxiliary regression. The error structure data were drawn from a normal distribution with mean, zero and variance, .

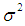iii. The sample sizes for the simulation were 10 and 30, 50 and 100, 150 and 200 for small, medium and large sample sizes respectively. Each experiment was replicated in 10,000 times.

iv. The levels of heteroscedasticity, 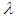, introduced were 0.1, 0.5 and 0.9 for mild, moderate and severe heteroscedasticity respectively.

v. The Harvey (1976) model of multiplicative heteroscedasticity error structure was assumed with general formulation

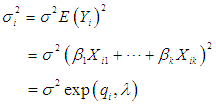Where 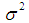and 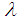are both unknown real constants, which determine the levels or degree of heteroscedasticity.

The following five tests were considered in this paper namely; Breusch-Pagan (1979), White (1980), Glejser (1969), Park (1966) and Goldfeld-Quandt (1965).

4. Results and Discussion

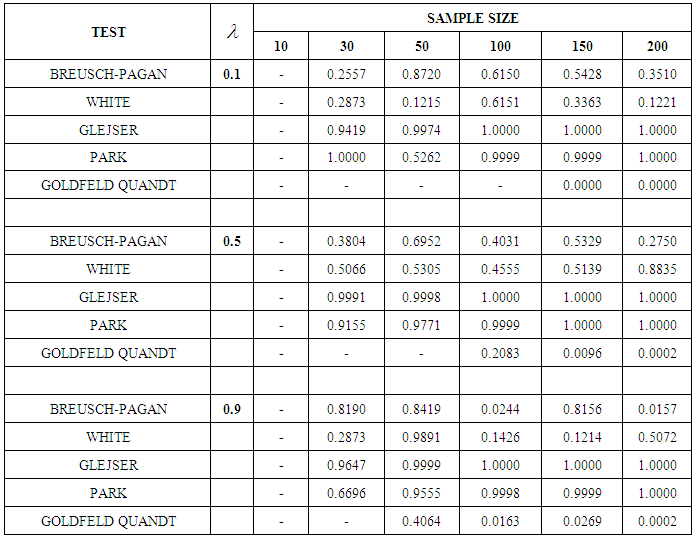
Table 1 shows the power of the tests for Cobb-Douglas Model at 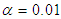. There is no result for sample size 10 at all levels of heteroscedasticity 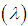for all the tests due to insufficient sample size. The result revealed that at every level of heteroscedasticity, as the sample size increases, the power of the test for Glejser and Park test improves and remains powerful. It can also be seen that at 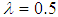, the power of the test for White also improved. When the sample size is equal to 50, the power of all tests improved at both 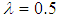and 0.9. Goldfeld-Quandt test is not a reliable test at all levels of heterogeneity and sample sizes.

Table 1. Power of the Tests for Cobb-Douglas Model at α = 0.01

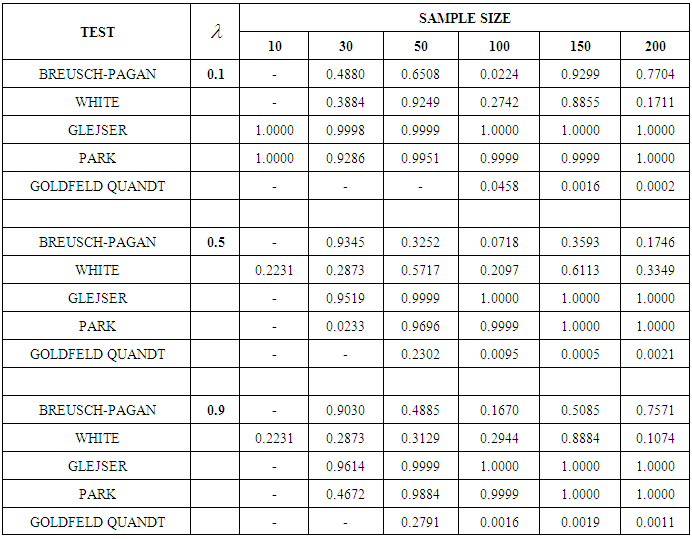
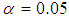Table 2 shows the power of the tests for Cobb-Douglas Model at . The result shows that at every level of heteroscedasticity, as the sample size increases, Glejser and Park tests are powerful. It can also be seen that at 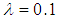when n =50 and 150 all the powers of test improved except Goldfeld-Quandt test, likewise, at 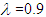when n=150.

Table 2. Power of the Tests for Cobb-Douglas Model at α = 0.05

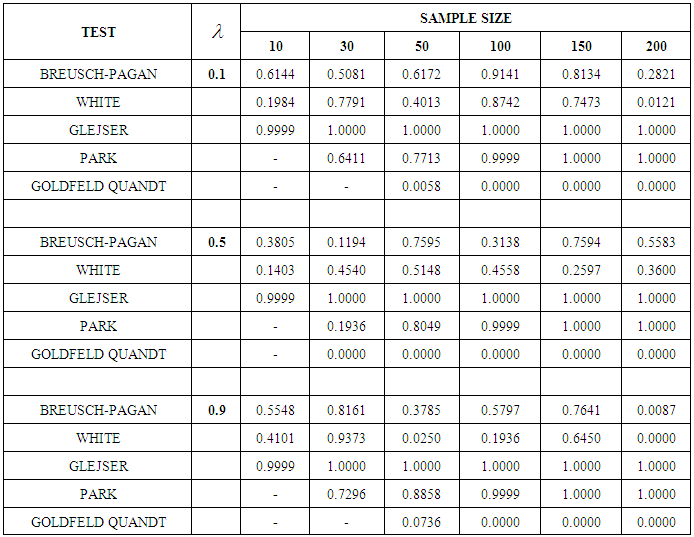
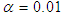Table 3 shows the power of the tests for Exponential Model at . The result shows that at every level of heteroscedasticity, as the sample size increases, the power of the test for Glejser and Park test is very high. The power of the test for Breusch-Pagan test also improves as sample size increases when 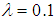expect when n=200. The power of all the tests improved when 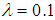at n=30, 100 and 150 also when 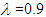at n=30 and 150. Goldfeld-Quandt test is still not a reliable test at all levels of heterogeneity and sample sizes.

Table 3. Power of the Tests for Exponential Model at α = 0.01

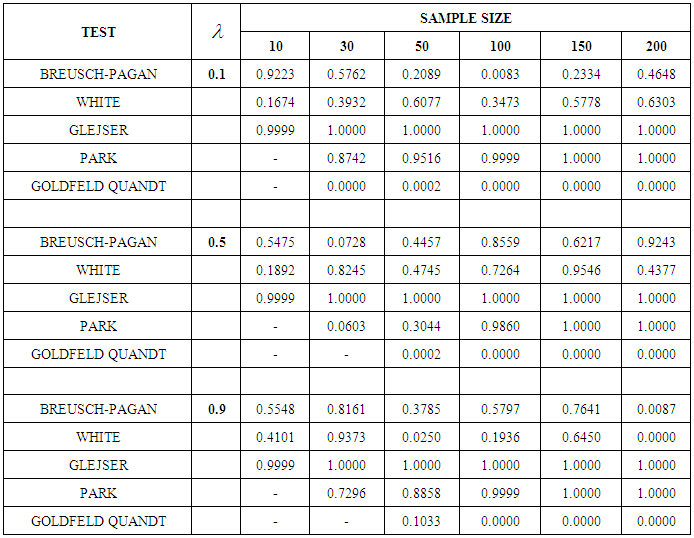
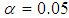Table 4 shows the power of the tests for Exponential Model at . The result shows that at every level of heteroscedasticity, as the sample size increases, the power of the test for Glejser and Park test is powerful. The power of all the tests improves at 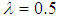when n=100 and 150, so also, at 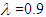when n=30 and 150 expect for Goldfeld-Quandt test.

Table 4. Power of the Tests for Exponential Model at α = 0.05

5. Conclusions

The results obtained from the analysis conform to the asymptotic property as sample sizes increases, the power of the two tests namely, Glejser and Park, is more powerful at every level of heteroscedasticity for the two models. It can therefore be concluded from this study that Glejser and Park tests should be used for detecting the heteroscedasticity when nonlinear models are used in analyzing data.