Maxwell Akwasi Boateng1, Akoto Yaw Omari-Sasu2, Richard Kodzo Avuglah2, Nana Kena Frempong2
1Faculty of Engineering, Ghana Technology University College, Ghana
2Department of Mathematics, Kwame Nkrumah University of Science and Technology, Ghana
Correspondence to: Maxwell Akwasi Boateng, Faculty of Engineering, Ghana Technology University College, Ghana.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The study focused on the likelihood of a pair of random variables having either an Archimedean copula or an Elliptical copula. The study involved simulating several pairs of random variables and the bicopselect () function in R was used to select an appropriate bivariate copula family for simulated pairs of random variables. The corresponding parameter estimates were obtained by maximum likelihood estimation. The method compared AICs of the various bivariate copulas under consideration. In all, about forty (40) bivariate copulas were considered ranging from one parameter models to two parameter models, three parameter models and in some cases rotations of some of these models. Fifty (50) different pairs of random variables were simulated for sample sizes 30, 300, 1000, 10000, 100000 and 1000000. For sample size thirty (30), 47 pairs had their copulas being Archimedean, for sample size 300, 47 had their copulas being Archimedean, for sample sizes 1000, 10000, 100000 and 1000000, 49, 44, 47 and 46 pairs respectively had their copulas being Archimedean. The results showed that between the Archimedean and Elliptical copulas, the Archimedean copulas were the most likely to fit the simulated pairs of random variables.
Keywords:
Archimedean copulas, Elliptical copulas, Simulation, Random variables
Cite this paper: Maxwell Akwasi Boateng, Akoto Yaw Omari-Sasu, Richard Kodzo Avuglah, Nana Kena Frempong, On Two Random Variables and Archimedean Copulas, International Journal of Statistics and Applications, Vol. 7 No. 4, 2017, pp. 228-237. doi: 10.5923/j.statistics.20170704.05.
1. Introduction
A copula is a function which joins or couples a multivariate distribution function to its one-dimensional marginal distribution functions. Over the years, copulas have played an important role in several areas of statistics. According to Fisher (1997), specifically his notes in the Encyclopedia of Statistical Sciences, “Copulas are of interest to statisticians for two main reasons; First, as a way of studying scale-free measures of dependence; and secondly, as a starting point for constructing families of bivariate distributions.One attractive property of copulas is their invariance under strictly increasing transformations of the margins. Copulas have been thoroughly reviewed in Nelsen (2006). Copula was first used in financial applications by Embrechts et. al. (2002). Since then the application on copula theory in finance and economics has grown tremendously. Moreover, practical applications of this modeling approach are found in fields such as finance (Nikoloulopoulos et. al. (2012); Fang and Madsen (2013)), hydrology (Genest et. al. (2007)), public health and medical (Winkelmann (2012)) and actuarial science (Frees and Valdez (1998); Otani and Imai (2013)).An important class of copulas are the Archimedean copulas, they are discussed in [Genest and Mackay (1986), Joe (1997), McNeil and Neslehova (2009)]. Archimedean copulas are popular since they are easy to handle, have simple, closed-form expressions, and can be used to derive portfolio distributions (Crook and Moreira (2011)).Trede and Savu (2013) suggested a new straightforward method to check whether a copula is an Archimedean copula without specifying its parametric family. Their approach was applied to (bivariate) joint distributions of stock asset returns and they discovered that in general, stock returns may have Archimedean copulas.Archimedean copulas over the years have been successfully applied in various sectors (Louie (2014), Corbella and Stretch (2013) and Yee et. al (2014)).This study is to serve as a support to the works that seek to tie two random variables with the Archimedean copulas.
2. Copulas
A copula is a multivariate cumulative distribution function (CDF) whose univariate marginal distributions are all Uniform (0, 1). Suppose that 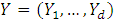 has a multivariate CDF
has a multivariate CDF 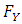 with continuous marginal univariate CDFs
with continuous marginal univariate CDFs 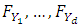 . If Y has a continuous CDF F, then
. If Y has a continuous CDF F, then 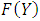 has a uniform (0, 1) distribution.
has a uniform (0, 1) distribution. 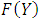 is often called the probability transformation of Y. This fact is easy to see if F is strictly increasing, since then
is often called the probability transformation of Y. This fact is easy to see if F is strictly increasing, since then 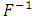 exists, so that
exists, so that 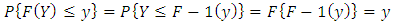 | (1) |
Then, by the equation above each of 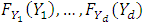 is distributed uniform (0, 1). Thus, the CDF of
is distributed uniform (0, 1). Thus, the CDF of  is a copula. This CDF is called the copula of Y and denoted by
is a copula. This CDF is called the copula of Y and denoted by 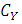 .
. 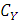 contains all information about dependencies among the components of Y but has no information about the marginal CDFs of Y.
contains all information about dependencies among the components of Y but has no information about the marginal CDFs of Y.
2.1. Archimedean Copulas
An Archimedean copula with a strict generator has the form;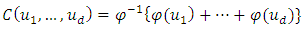 | (2) |
where the generator function 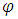 satisfies the following conditions:1.
satisfies the following conditions:1. 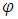 is a continuous, strictly decreasing, and convex function mapping [0,1] onto [0,∞].2.
is a continuous, strictly decreasing, and convex function mapping [0,1] onto [0,∞].2. 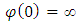 and 3.
and 3. 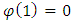
2.2. Elliptical Copulas
Elliptical copulas are the copulas of elliptically contoured distributions. The multivariate and the Student-t are the most commonly used elliptical distributions. The Normal copula is an elliptical copula given by: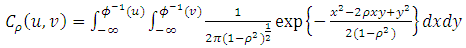 | (3) |
The Student-t copula is an elliptical copula defined by: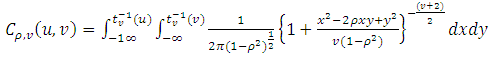 | (4) |
3. Simulations and Results
To assess the argument that the Copula of two random variables is more often than not Archimedean, several simulations are performed. Considering pairs of random variables of size, n each, the Vuong and Clarke tests for selecting a bivariate copula is used to assign copulas to each of the 50 pairs of random variables.The choice of a bivariate copula is between the elliptical (Gaussian and Student-t) and the Archimedean (Clayton, Gumbel, Frank, Joe, BB1, BB6, BB7 and BB8) copulas to cover a large range of dependence patterns. For Archimedean copula families, rotated versions were included to cover negative dependence as well. The Tawn copula being an asymmetric extension of the Gumbel copula with three parameters was added to the Archimedean. For simplicity, two versions of the Tawn copula with two parameters each were employed. Each type has one of the asymmetry parameters fixed to 1, so that the corresponding copula density is either left- or right-skewed (in relation to the main diagonal). For each of the possible pairs, the tests decide which family best fits the given data.
3.1. Algorithm
Step 1:Simulate two random variables x1 and x2 of equal length n, with uniform margins.Step 2:Using the Vuong and Clarke tests for selecting a bivariate copula, select a copula.Step 3:Repeat Step 1 for different values of n for 49 other pairs of simulated x1 and x2 and apply step 2 in each case.Example using R; set.seed(1)Step 1: Nsim=10000 #number of random numbersx1=runif(Nsim)x2=runif(Nsim) #vectors Step 2:selectedCopula <- BiCopSelect(x1,x2,familyset=NA)selectedCopulaTables 1, 2, 3, 4, 5 and 6 give the results of simulated pairs of random variables, selected copulas and in some cases their parameter values.
4. Results
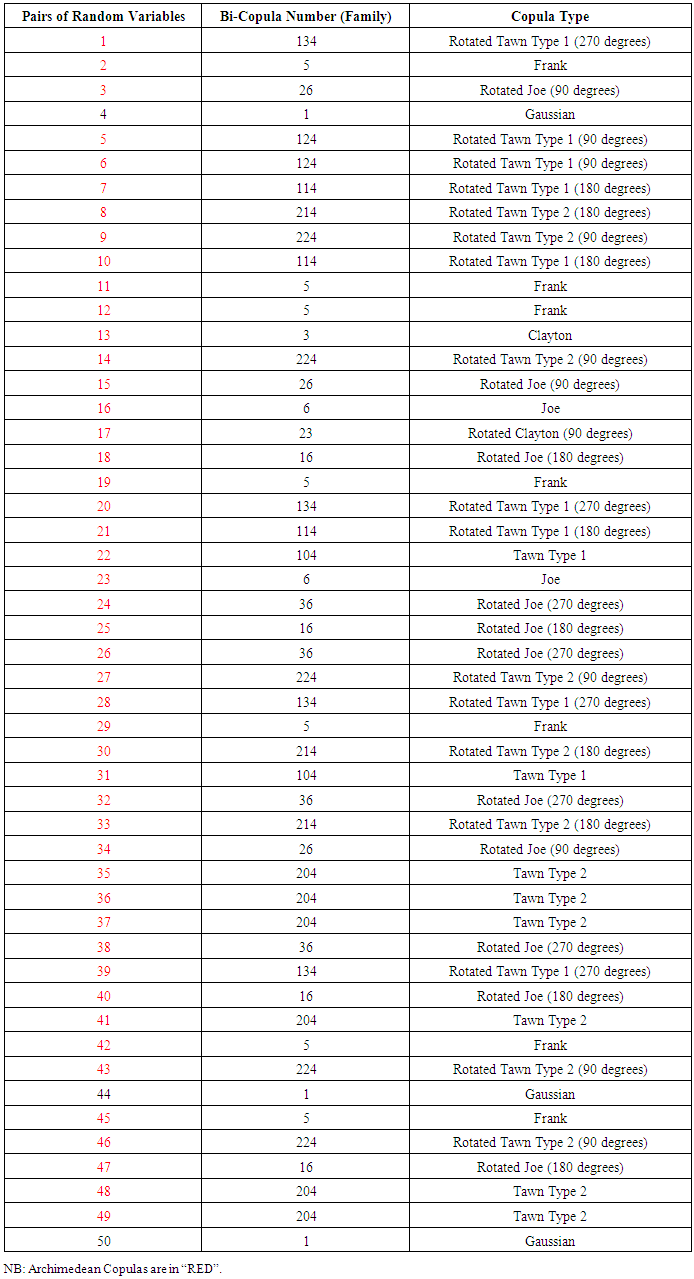
The results of the whole work is summarized in Tables 1, 2, 3, 4, 5, 6 and 7. Table 1. Pairs of Random Variables and Their Copulas (n=30)
 |
| |
|
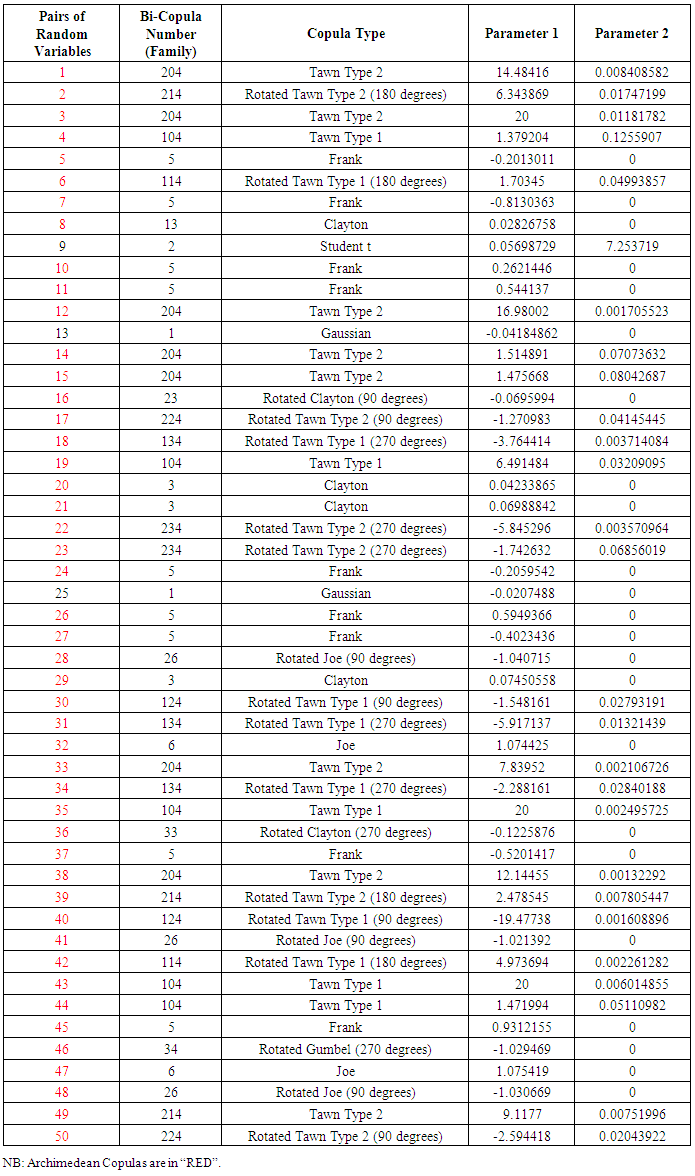
Table 2. Pairs of Random Variables and Their Copulas (n = 300)
 |
| |
|
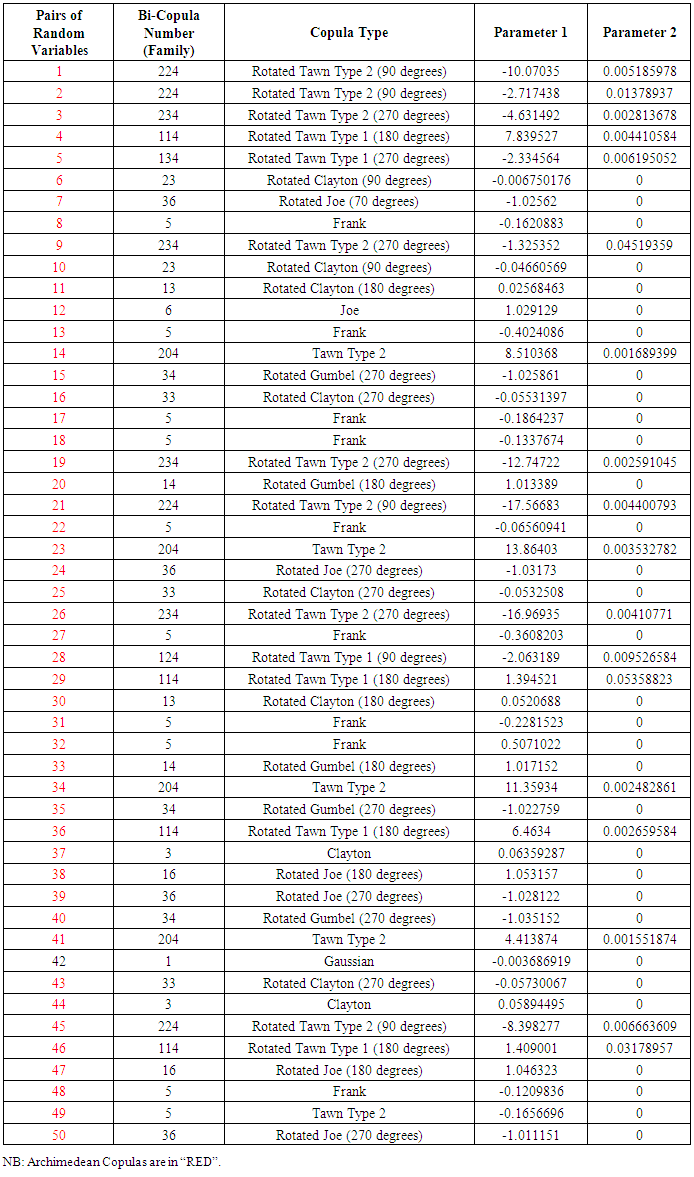
Table 3. Pairs of Random Variables and Their Copulas (n = 1000)
 |
| |
|
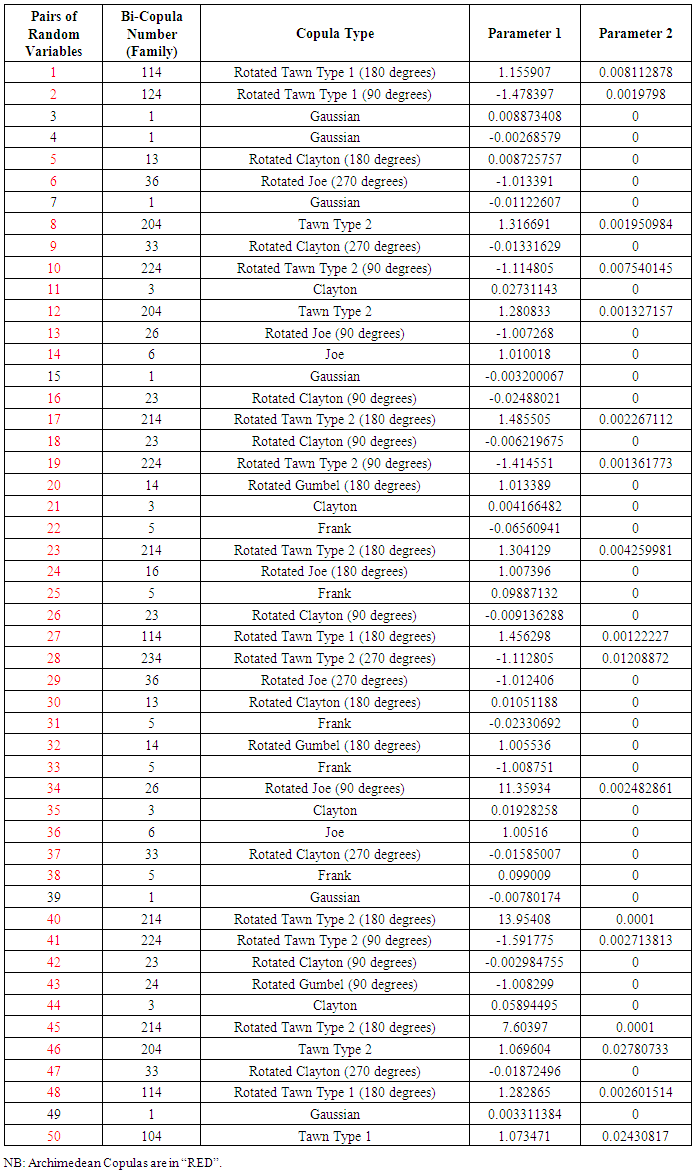
Table 4. Pairs of Random Variables and Their Copulas (n = 10000)
 |
| |
|
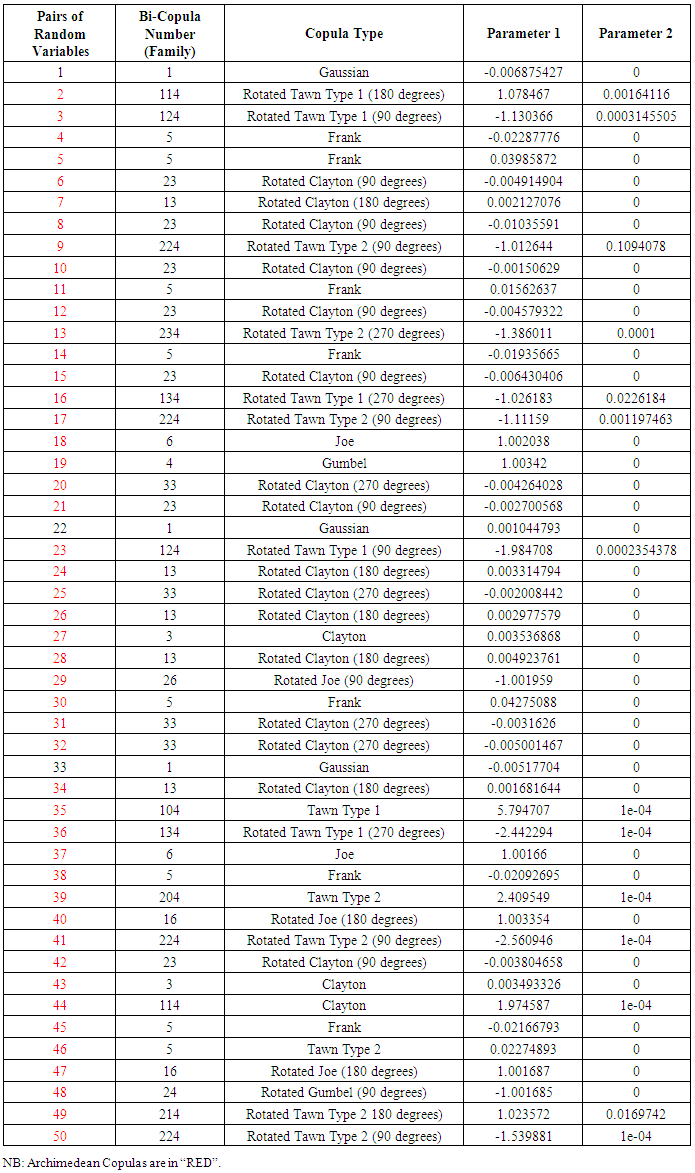
Table 5. Pairs of Random Variables and Their Copulas (n = 100000)
 |
| |
|
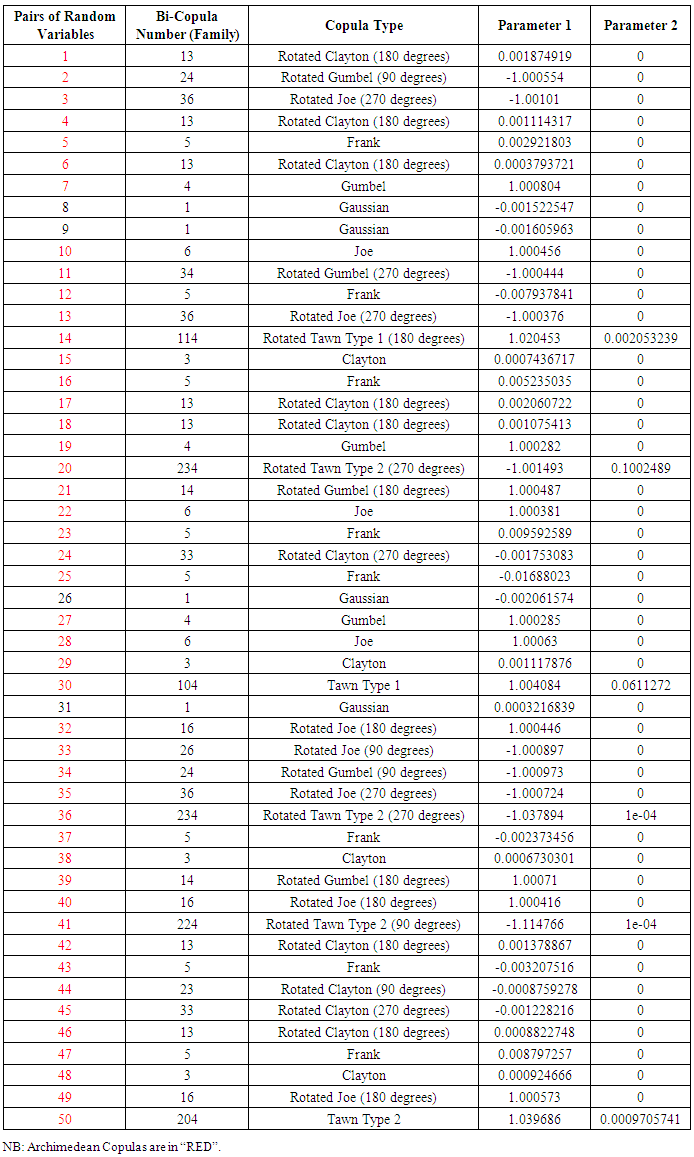
Table 6. Pairs of Random Variables and Their Copulas (n = 1000000)
 |
| |
|
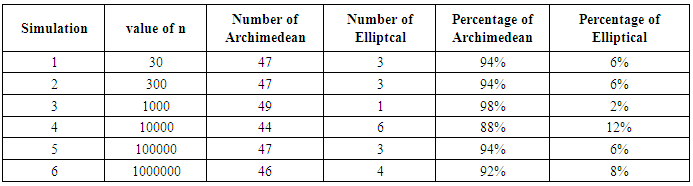
Table 7. Summary of simulation (for 50 runs)
 |
| |
|
Table 1 constitutes simulation 1 for 50 different simulated pairs of random variables subjected to the process in 4.1. Out of the 50 pairs of random variables simulated following the process in 4.1, 47 of the pairs had their copula being Archimedean Copulas. Only 3 (simulated pair 4, 44 and 50) had their copula being the Elliptical copulas (Gaussian).Table 2 shows results for simulation 2 made up of 50different pairs of simulated random variables. Out of the 50 pairs of random variables, 47 of them (in red) had their copula being Archimedean Copulas. Pairs 9, 13 and 25 however had their copula being the Elliptical copula (Gaussian and student t).From Table 3, out of the 50 pairs of random variables simulated, 49 of them (in red) had their copula being Archimedean Copulas and only one (pair 42) had its copula being Elliptical (Gaussian).From Table 4, out of the 50 pairs of random variables simulated, 44 of them (in red) had their copula being Archimedean Copulas and 6 of them (pairs 2, 3, 7, 15, 39 and 49) being Elliptical copulas (Gaussian).From Table 5, out of the 50 pairs of random variables simulated, 47 of them (in red) had their copula being Archimedean Copulas whereas 3 of the pairs (pair 1, 2 and 33) had their copula being Elliptical (Gaussian).From Table 6, out of the 50 pairs of random variables simulated, 46 of them (in red) had their copula being Archimedean Copulas and 4 of them (pairs 8, 9, 26 and 31) had their copula being Elliptical (Gaussian).Table 7 above indicates that for a run of 50 pairs of random variables with different number of data points (n=30, 300, 1000, 10000 and 1000000 respectively), the Archimedean copulas were the most likely to fit those pairs.
5. Conclusions
This study sought to check which bivariate copula (between the Archimedean and Elliptical copulas) was the most likely to fit two random variables. 50 pairs of random variables were simulated for sample sizes n = 30, n= 300, n= 1000, n = 10000, n = 100000 and n = 1000000. For all sample sizes under consideration, no regular pattern for the copula selection is observed. The question then is, “Is there a way to detect a relationship between the random variables and the copula selected?”. The study revealed that for all simulations under study, the most likely copula to best handle pairs of random variables were the Archimedean copulas. This study supports the argument that the copula of two random variables is Archimedean. It will however be interesting to delve deeper into what characteristics of the pairs of random variables that account for they being Archimedean or elliptical.
References
| [1] | Belgorodski, N. (2010), Selecting pair-copula families for regular vines with application to the multivariate analysis of European stock market indices, Diploma Thesis, http://mediatum.ub.tum.de/?id=1079284. |
| [2] | Clarke, K. A. (2007), A Simple Distribution-Free Test for Non nested Model Selection, Political Analysis, 15, 347-363. |
| [3] | Vuong, Q. H. (1989), Ratio tests for model selection and non- nested hypotheses, Econometrica 57 (2), 307-333. |
| [4] | R. B. Nelsen, An Introduction to Copulas, 2nd ed., Springer, New York, 2006. |
| [5] | P. Embrechts, A. McNeil and D. Straumann, “Correlation and Dependence in Risk Management: Properties and Pitfalls,” Risk management: value at risk and beyond, pp. 176-223, 2002. |
| [6] | K. Nikoloulopoulos, H. Joe and H. Li. ”Vine copulas with asymmetric tail dependence and applications to financial return data.” Computational Statistics & Data Analysis, vol. 56, no. 11, pp. 36593673, 2012. |
| [7] | Y. Fang and L. Madsen, “Modified Gaussian Pseudo-Copula: Applications in Insurance and Finance,” Insurance Mathematics and Economics, vol. 53, pp. 292-301, 2013. |
| [8] | C. Genest, A. C. Favre, J. B´eliveau and C. Jacques, “Meta elliptical Copulas and Their Use in Frequency Analysis of Multivariate Hydrological Data,” Water Resources Research, vol. 43, no. 9, 2007. |
| [9] | E. W. Frees and E. A. Valdez, “Understanding Relationships Using Copulas,” North American Actuarial Journal, vol. 2, pp. 1-25, 1998. |
| [10] | Y. Otani and J. Imai, “Pricing Portfolio Credit Derivatives with Stochastic Recovery and Systematic Factor.” IAENG International Journal of Applied Mathematics, vol. 43, no. 4, pp. 176-184, 2013. |
| [11] | R. Winkelmann, “Copula bivariate probit models: with an application to medical expenditures.” Health Economics, vol. 21, no. 12, pp. 14441455, 2012. |
| [12] | Mark Trede and Cornelia Savu, “Do stock returns have an Archimedean copula?”, Journal of Applied Statistics Vol. 40, Iss. 8, 2013. |
| [13] | Henry Louie (2014), “Evaluation of bivariate Archimedean and elliptical copulas to model wind power dependency structures; Wind Energy, Pages 225-240: 10.1002/we.1571. |
| [14] | S. Corbella, D. D. Stretch (2013), “Simulating a multivariate sea storm using Archimedean copulas”, Coastal Engineering, 76, 68 -78, https://doi.org/10.1016/j:coastaleng.2013.01.011. |
| [15] | K. C. Yee, J. Suhaila, F. Yusof, F. H. Mean, “Bivariate copula in fitting rainfall data, AIP conference Proceedings 1605, 986 (2014); http://dx.doi.org/10.1063/1.4887724. |
| [16] | Fisher, N. I. (1997). Copulas. In: Encyclopedia of Statistical Sciences, Update Vol.1, 159-163. John Wiley Sons, New York. |
| [17] | C. Genest and J. MacKay, The joy of copulas: Bivariate distributions with uniform marginals, Amer. Statist. 40(4) (1986), pp. 280–283. |
| [18] | H. Joe, Multivariate Models and Dependence Concepts, Chapman and Hall, London, 1997. |
| [19] | A.J. McNeil and J. Neslehová, Multivariate Archimedean copulas, d-monotone functions and l-norm symmetric distributions Ann. Statist. 37 (2009), pp. 3059–3097. |
| [20] | J. Crook and F. Moreira, Checking for asymmetric default dependence in a credit card portfolio: A copula approach, J. Empir. Finance 18(4) (2011), pp. 728–742. |


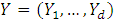 has a multivariate CDF
has a multivariate CDF  with continuous marginal univariate CDFs
with continuous marginal univariate CDFs 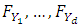 . If Y has a continuous CDF F, then
. If Y has a continuous CDF F, then 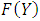 has a uniform (0, 1) distribution.
has a uniform (0, 1) distribution. 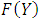 is often called the probability transformation of Y. This fact is easy to see if F is strictly increasing, since then
is often called the probability transformation of Y. This fact is easy to see if F is strictly increasing, since then 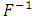 exists, so that
exists, so that 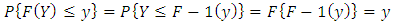
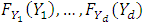 is distributed uniform (0, 1). Thus, the CDF of
is distributed uniform (0, 1). Thus, the CDF of  is a copula. This CDF is called the copula of Y and denoted by
is a copula. This CDF is called the copula of Y and denoted by 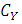 .
. 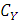 contains all information about dependencies among the components of Y but has no information about the marginal CDFs of Y.
contains all information about dependencies among the components of Y but has no information about the marginal CDFs of Y.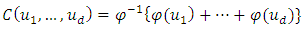
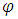 satisfies the following conditions:1.
satisfies the following conditions:1. 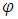 is a continuous, strictly decreasing, and convex function mapping [0,1] onto [0,∞].2.
is a continuous, strictly decreasing, and convex function mapping [0,1] onto [0,∞].2. 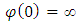 and 3.
and 3. 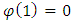
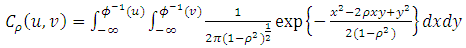
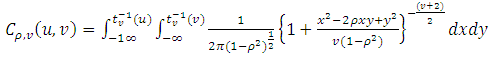
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





