-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2017; 7(3): 192-195
doi:10.5923/j.statistics.20170703.05

Statistical Assessment of Some Factors Affecting Calving Interval by Using Ordinal Logistic Regression in Holstein Cows
Fatma D. M. Abdallah 1, Eman A. Abo Elfadl 2
1Department of Animal Wealth Development, Faculty of Veterinary Medicine, Zagazig University, Egypt
2Department of Animal Husbandry and Development of Animal Wealth, Faculty of Veterinary Medicine, Mansoura University, Egypt
Correspondence to: Eman A. Abo Elfadl , Department of Animal Husbandry and Development of Animal Wealth, Faculty of Veterinary Medicine, Mansoura University, Egypt.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Background & objectives: Calving interval considered an important trait throughout Holstein dairy cow's life. There are many risk factors which have a great impact on it. In the line with this consideration, the purpose of this study is to apply ordinal logistic regression model to estimate the effect of these risk factors on calving interval. Methods: Ordinal logistic regression analysis was used to estimate the odds ratio (OR) and probability of Holstein dairy cows conception for 3400 lactation records from Dina farms company, Egypt. The data was collected over a period extended from 1998 to 2010. The logit link function was used to predict the probability of occurrence of pregnancy using SPSS version 20.0, USA. Results: The odds ratio showed that the likelihood of pregnancy in cows with different parities was 0.931, 0.787, 0.634 and 1.000 for lactation order 2, 3, 4 and 5 respectively. Odds ratio of pregnancy of cows calving in winter were higher than those calving in summer, it was 1.234 and 1.000 respectively. Odds of different periods of days open were 0.586, 0.771, 0.638 and 1.000 respectively. Odds of different periods of dry period were 0.378, 0.525, 0.545 and 1.000 respectively. Conclusions: Findings showed fitting of this model to the data, it also showed the ability of ordinal logistic regression to provide measure which facilitates understanding of the important risk factors affecting calving interval.
Keywords: Calving interval, Pregnancy, Ordinal logistic regression, Odds ratio
Cite this paper: Fatma D. M. Abdallah , Eman A. Abo Elfadl , Statistical Assessment of Some Factors Affecting Calving Interval by Using Ordinal Logistic Regression in Holstein Cows, International Journal of Statistics and Applications, Vol. 7 No. 3, 2017, pp. 192-195. doi: 10.5923/j.statistics.20170703.05.
Article Outline
1. Introduction
- Logistic regression analysis is a regression model where the dependent variable (DV) is categorical; it is divided into binary, multinominal and ordinal logistic regression analysis, depending on the scale type and the number of categories of the dependent variable. It is also divided into univariate and multivariate logistic regression according to the number of risk factors [1].Ordinal logistic regression is a new statistical method used to analyze ordered categorical response variables. It is called the proportional odds model.These models are now available to make full use of ordered data but they are not used on a large scale [2].The term logistic regression analysis originated from logit transformation, which is applied to the dependent variable and this causes certain differences both in estimation and interpretation [3].Maximum likelihood method is used in logistic regression analysis to obtain coefficients, as an important step in the analysis process before the application of logistic regression analysis [4, 5].Logistic regression provides a measure of interest which is called odds ratio (OR). An odd is defined as the probability of an event (in this case pregnancy) occurring (p) divided by 1 - p. Odds ratios provided by multiple logistic regression (the antilogarithm of the coefficient for an independent variable) are conditional upon all other variables in the model.
2. Material and Methods
2.1. Source of Data
- Data of 3400 lactation records for Holstein dairy cows were collected from records of Holstein Friesian cattle maintained at Alexandria-Copenhagen dairy farm, 76 km Alexandria-Cairo desert road during the period extended from 1998 to 2010.
2.2. Studied Variables
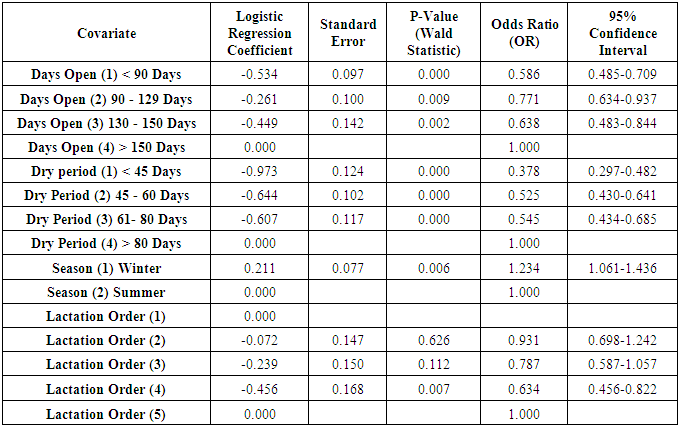
- Days open (DO): The period per days between calving and next conception in cows, it is also called calving-to-conception interval.Calving interval (CI): The average time interval per days between two successful calving.Dry period (DP): The period during the lactation cycle when the cow is not lactating, i.e. the period between the end of the lactation and the beginning of the next one.Season and lactation order (parity): Number of lactation season.The data prepared and coding:First step of this analysis was to change Continuous data to categorical data including calving interval, days open and dry period.v Data of calving interval were categorized into three categories (≤ 365 days =1, 366-424 days = 2 and < 424 days = 3).v Data for effect of days open were categorized into four categories (< 90 days = 1, 90-129 days = 2, 130-150 = 3 and < 150 days = 4).v Data for dry period effects were categorized into four categories (< 45 days = 1, 45-60 days = 2, 61-80 days = 3 and < 80 days = 4).v Data for lactation order were categorized into five categories (P1 to P5).v Data for season effects were categorized into two categories (winter = 1 and summer = 2).All these variables were entered into the equation as independent variables except calving interval which is the dependent or the outcome variable.
2.3. Statistical Analysis
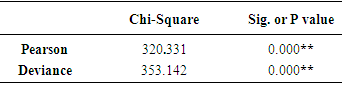
- Multivariable logistical regression procedure was used; to determine the effect of some risk factors including (lactation order, calving season, days open and dry period) on calving interval. Rate was examined, simultaneously. The multivariable logistical regression model was constructed using the PLUM procedure of [6].Maximum likelihood value of the baseline model, Wald statistics to test significance of variables and Exp (B) or exponentiated logistic coefficients were assessed [7].Cox & Snell R2, Nagelkerke R2 and McFadden values are different ways of prediction of the explained variance in the dependent variable by the model and are interpreted as R2 in multiple regression [8]. Hosmer and Lemeshow chi-squared goodness of fit test assess whole fitness of the logistic regression model. It is more powerful than chi-square test when predictive variables are constant variables or when there is a small sample [9] The important measure in logistic regression is the odds ratio (OR) which is the probability of an event occurring (p) divided by 1 - p. It is the antilogarithm of the coefficient for an independent variable which is equal to exp (β), or sometimes written eβ. Some authors use the Greek symbol ψ (psi, pronounced like "sci" in science) to refer to the odds ratio, and others use OR or O.R. For the analysis process, independent variables divided into categories. One category was considered as the reference category for odds ratio (OR = 1). An OR of >1 indicates increased likelihood while an OR <1 indicates an inverse association. The outcome for each category of independent variable was compared to reference group for that variable. A cumulative logit model approach using PLUM procedure in SPSS was used. Statistical significance for all models was defined as P value < 0.05.The specific form of the ordinal logistic regression model:If Y is ordinal, cumulative odds or cumulative logits is used to take ordering in consideration.Consider k+1 is the ordered categories and defined by
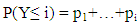 | (1) |
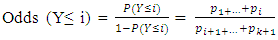 | (2) |
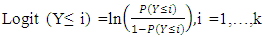 | (3) |
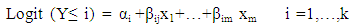 | (4) |
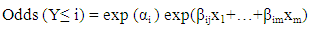 | (5) |
3. Results
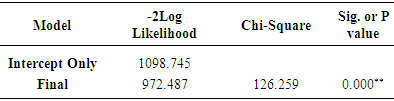
- The results showed fitting of overall model to the data using -2 log likelihood = 972.487 with a p-value 0.000** which is highly significant, so the covariates have a significant effect on the probability of pregnancy as shown in Table 1.
|
|
|
|
4. Conclusions
- Regression analysis was used as statistical methods for evaluation of some risk factors that affect calving interval in dairy cattle. Result of this study showed Regression models can be used when the dependent is represented by an ordinal variable. The relationship between explanatory variables and the outcome can be represented by the proportional odds model. Ordinal regression is a powerful tool, easy to use, and produces an interpretable parameter that summarizes the effect between groups over all levels of the outcome. It also showed the ability of ordinal logistic regression to provide measure which facilitates understanding of the important risk factors affecting calving interval, Future studies are needed for further confirmation of this results.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML