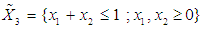-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Statistics and Applications
p-ISSN: 2168-5193 e-ISSN: 2168-5215
2017; 7(2): 73-92
doi:10.5923/j.statistics.20170702.03

Competitive Assessment of Two Variance Weighted Gradient (VWG) Methods with Some Standard Gradient and Non-Gradient Optimization Methods
Otaru O. A. P., Iwundu M. P.
Department of Mathematics and Statistics, University of Port Harcourt, Port Harcourt, Nigeria
Correspondence to: Iwundu M. P., Department of Mathematics and Statistics, University of Port Harcourt, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A competitive assessment of the performance of two Variance Weighted Gradient (VWG) methods with some gradient and non-gradient optimization methods is considered for optimizing polynomial response surfaces. The variance weighted gradient methods could involve several response surfaces defined on joint feasible regions having same constraints or several response surfaces defined on disjoint feasible regions having different constraints. The gradient and non-gradient optimization methods include Quasi-Newton (GN), Genetic Algorithm (GA), Mesh Adaptive Search (MADS) and Generalized Pattern Search (GPS) methods. The variance weighted gradient methods perform considerably and comparatively well and require few iterative steps to convergence.
Keywords: Response Surfaces, Optimization, Gradient Method, Non-Gradient Method, Weighted Gradients methods
Cite this paper: Otaru O. A. P., Iwundu M. P., Competitive Assessment of Two Variance Weighted Gradient (VWG) Methods with Some Standard Gradient and Non-Gradient Optimization Methods, International Journal of Statistics and Applications, Vol. 7 No. 2, 2017, pp. 73-92. doi: 10.5923/j.statistics.20170702.03.
Article Outline
1. Introduction
- Gradient and non-gradient methods are popular techniques used in optimizing response functions. They have been very helpful in handling optimization of single objective functions. In the presence of multi-objective functions, the popularly used one-at-a-time optimization techniques become time consuming. In fact, the challenge in getting a good guess of starting point introduces cycling and sometime lack of convergence. The Gradient and non-gradient methods include Newton Method (NM), Guasi-Newton Method (GNM), Genetic Algorithm (GA), Mesh Adaptive Search (MADS) and Generalized Pattern Search (GPS) methods, etc. These methods could readily be seen in statistical software and thus, easy to use in handling optimization problems. As documented in Patil and Verma (2009), the Newton method was developed by Newton in 1669 and was later improved by Raphson in 1690 and hence popularly referred to as Newton-Raphson’s iterative algorithm. NM is the commonly applied gradient-based method for optimizing polynomial function when the first and second derivative of the function is explicitly available. It assumes that the function can be locally approximated as a quadratic in the region around the optimum. Newton method requires computation of Hessian matrix and the convergence of the method is slow. Davidon (1959) developed the Quasi Newton Method (QNM) which was later popularized by Fletcher and Powell (1963). The Quasi Newton Method can be used if the Hessian matrix is unavailable or too expensive to compute at all iterations. Thus the Quasi Newton Method helps to reduce computational rigor involved in the Newton method. Commonly used Quasi Newton algorithms are the SR1 formular, the BHHH method, the BFGS method and the L-BFGS method. Holland (1975) developed Genetic Algorithms (GAs) for linear and non-linear functions optimization. The algorithm solves both constrained and unconstrained optimization problems using natural procedure that imitates biological evolution. Genetic Algorithms can be used to solve problems where standard optimization techniques do not apply as well as problems in which the objective function is discontinuous or non-linear. Pattern search algorithms can also be employed in getting optimal solutions. The generalized pattern search (GPS) for unconstrained optimization problems is due to Torczon (1997) and does not require information about the gradient or higher derivative to arrive at the optimal point. Audet and Dennis Jr (2006) developed the Mesh Adaptive Direct Search (MADS) as a class of algorithm that extends the generalized pattern search. Both algorithms compute a sequence of points that approach the optimal solutions. Abramson et.al (2009) applied the Mesh adaptive direct search in solving constrained mixed variable optimization problems in which variables may be continuous or categorical. The gradient-free class of Mesh adaptive direct search algorithm is called Mixed Variable MADS abbreviated MV-MADS. Audit et.al (2010) introduced MULTIMAD, a multi-objective Mesh adaptive direct search optimization algorithm. For more on the Gradient and non-gradient methods, see Audet and Dennis Jr (2009), Audet et.al (2014), Dolan et.al (2003), Goldberg (1989), Kolda et.al (2003), Lewin (1994a), Lewin (1994b), Lewis and Torczon (2000).Iwundu et.al (2014) developed an iterative variance weighted gradient procedure that can simultaneously optimize multi-objective functions defined on the same region or having the same constraints. When the constraints are different and the regions are disjoint, a projection scheme that allows the projection of design points from one region to another is used. The performance of the variance weighted gradient method due to Iwundu et al. (2014) and its modified projection scheme technique shall be compared with the gradient-based QNM and non-gradient optimization methods, namely, GA, MADS and GPS. The basic algorithmic steps of the variance weighted gradient methods are presented in section 2.
2. Methodology
- We present the algorithmic steps of the variance weighted gradient method for joint feasible region as well as for disjoint feasible region.
2.1. Variance Weighted Gradient (VWG) Method for Joint Feasible Regions with Same Constraints
- Let
 be an n-variate, p-parameter polynomial functions of degree m defined by constraints on the same feasible region, given by
be an n-variate, p-parameter polynomial functions of degree m defined by constraints on the same feasible region, given by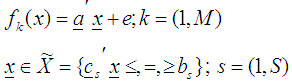 | (1) |
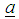 is a p-component vector of known coefficient,
is a p-component vector of known coefficient, 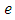 is the random error component assumed normally and independently distributed with zero mean and constant variance,
is the random error component assumed normally and independently distributed with zero mean and constant variance, 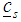 is a component vector of known coefficients and
is a component vector of known coefficients and 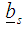 is a scalar for s number of constraints. The Variance Weighted Gradient (VWG) method for joint feasible regions with same constraints is defined by the following iterative steps:i) Obtain N support points
is a scalar for s number of constraints. The Variance Weighted Gradient (VWG) method for joint feasible regions with same constraints is defined by the following iterative steps:i) Obtain N support points 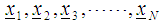 from
from 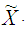 ii) Define the design measures
ii) Define the design measures 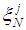 which is made up of N support points such that
which is made up of N support points such that 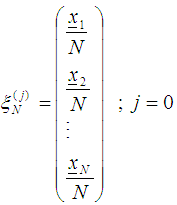 where
where  support points are spread evenly in
support points are spread evenly in  iii) From the support point l (1, N) that makes up the design measure, compute the starting points as.
iii) From the support point l (1, N) that makes up the design measure, compute the starting points as.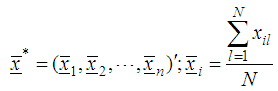 iv) Obtain the n-component gradient vector for the kth function.
iv) Obtain the n-component gradient vector for the kth function.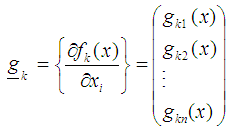 where
where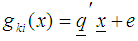 is an
is an  degree polynomial;
degree polynomial; 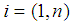
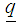 is a t-component vector of known coefficients v) Compute the corresponding kth gradient vector, by substituting each l design point to the gradient function
is a t-component vector of known coefficients v) Compute the corresponding kth gradient vector, by substituting each l design point to the gradient function 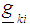 as
as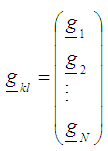 vi) Using the gradient function and design measures obtain the corresponding design matrices
vi) Using the gradient function and design measures obtain the corresponding design matrices 
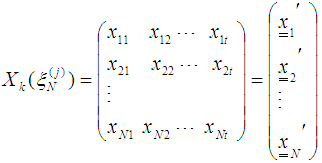 In order to form the design matrix
In order to form the design matrix  a single polynomial that combines the respective gradient function
a single polynomial that combines the respective gradient function  associated with each response function
associated with each response function  is
is 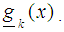 vii) Compute the variances of each l design point
vii) Compute the variances of each l design point 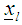 for the kth function as
for the kth function as 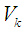
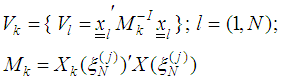 viii) Obtain the direction vector for the kth function as
viii) Obtain the direction vector for the kth function as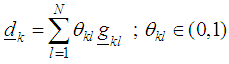 and the normalize direction vector
and the normalize direction vector 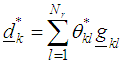 such that
such that 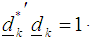 ix) Compute the step-length
ix) Compute the step-length 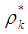 as
as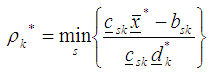 x) With
x) With 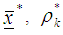 and
and 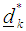 make a move to
make a move to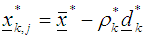 xi) To make a next move set
xi) To make a next move set 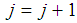 and define the design measure as
and define the design measure as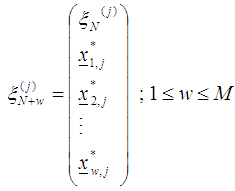 and repeat the process from step (iii) then obtain
and repeat the process from step (iii) then obtain 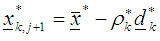 xii) If
xii) If 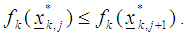 where
where 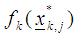 is the kth function at the jth step and
is the kth function at the jth step and 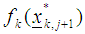 is the kth function at the next (j+1)th step.then set the optimizers as
is the kth function at the next (j+1)th step.then set the optimizers as 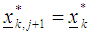 and STOP. Else, set
and STOP. Else, set 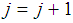 and repeat the process from (iii).
and repeat the process from (iii).2.2. Variance Weighted Gradient (VWG) Method for Disjoint Feasible Regions with Different Constraints
- Let
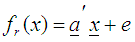 | (2) |
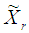 supported by s constraints. Such that
supported by s constraints. Such that 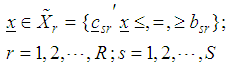 where
where 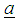 is a p-component vector of known coefficients, independent random variable
is a p-component vector of known coefficients, independent random variable 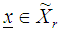 and
and 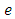 is the random error component assumed normally and independently distributed with zero mean and constant variance. While
is the random error component assumed normally and independently distributed with zero mean and constant variance. While 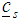 is a component vector of know coefficients and
is a component vector of know coefficients and 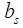 is a scalar for s number of constraints in the rth region.The Variance Weighted Gradient (VWG) method for disjoint feasible regions, with different Constraints, is given by the following sequential steps:i) From
is a scalar for s number of constraints in the rth region.The Variance Weighted Gradient (VWG) method for disjoint feasible regions, with different Constraints, is given by the following sequential steps:i) From 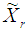 obtain the design measures
obtain the design measures 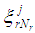 which are made up of support points from respective regions such that
which are made up of support points from respective regions such that 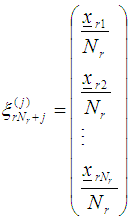 where
where 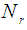 support points are spread evenly in
support points are spread evenly in 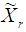 ii) From the support points that make up the design measure compute R starting points as, the arithmetic mean vectors.
ii) From the support points that make up the design measure compute R starting points as, the arithmetic mean vectors. 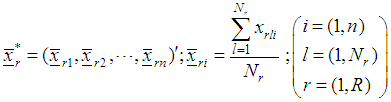 iii) Obtain the n-component gradient function for the rth region.
iii) Obtain the n-component gradient function for the rth region.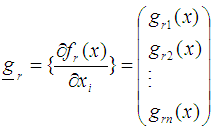 where
where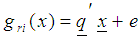 is an
is an 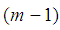 degree polynomial ;
degree polynomial ; 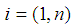
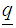 is a t-component vector of known coefficients iv) Compute the corresponding r gradient vectors, by substituting each design point defined on the rth region to the gradient function
is a t-component vector of known coefficients iv) Compute the corresponding r gradient vectors, by substituting each design point defined on the rth region to the gradient function 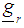 as
as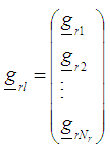 v) Using the gradient function and design measures obtain the corresponding design matrices
v) Using the gradient function and design measures obtain the corresponding design matrices 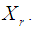
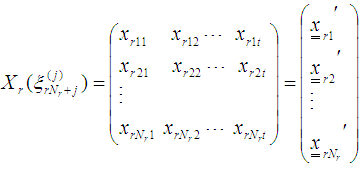 In order to form the design matrix
In order to form the design matrix 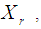 a single polynomial that combines the respective gradient function
a single polynomial that combines the respective gradient function 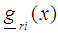 associated with each response function
associated with each response function 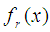 is
is 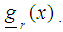 vi) Compute the variances of each l design point
vi) Compute the variances of each l design point 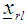 defined on the rth region as
defined on the rth region as 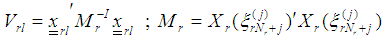 vii) Obtain the direction vector in the rth region as
vii) Obtain the direction vector in the rth region as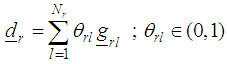 and the normalize direction vector
and the normalize direction vector 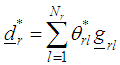 such that
such that 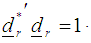 viii) Compute the step-length
viii) Compute the step-length 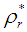 as
as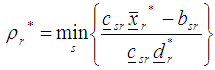 with
with 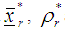 and
and 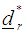 make a move to
make a move to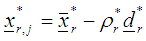 using
using 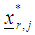 evaluate the projection operator
evaluate the projection operator 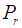 as
as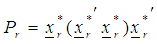 and obtain the projector optimizers for each region
and obtain the projector optimizers for each region 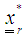 as
as 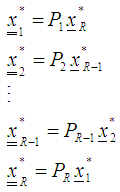 ix) To make a next move set
ix) To make a next move set 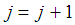 and define the design measure as
and define the design measure as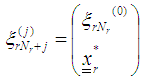 and repeat the process from step (ii) then obtain
and repeat the process from step (ii) then obtain 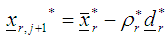 x) If
x) If 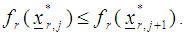 where
where 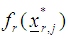 is the rth feasible region at the jth step and
is the rth feasible region at the jth step and 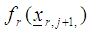 is the rth feasible region at the next j+1th step.then set the optimizers as
is the rth feasible region at the next j+1th step.then set the optimizers as 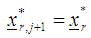 and STOP. Else, set
and STOP. Else, set 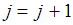 and repeat the process from (ii).
and repeat the process from (ii).3. Results
- In comparing the Variance Weighted Gradient (VWG) algorithms with standard gradient and non-gradient methods, we consider the optimization problems;Problem 1Minimize
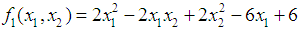 subject to
subject to 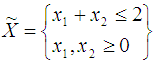 (Ghadle and Pawar, 2015)and Maximize
(Ghadle and Pawar, 2015)and Maximize 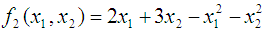 subject to
subject to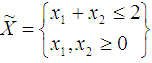 (Hillier and Lieberman, 2001).The solution to the minimization problem
(Hillier and Lieberman, 2001).The solution to the minimization problem 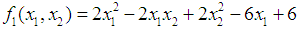 using the Variance Weighted Gradient (VWG) method is
using the Variance Weighted Gradient (VWG) method is 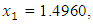
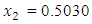 and
and 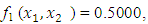 from an initial starting point,
from an initial starting point, 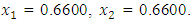 Similarly, the solution to the maximization problem
Similarly, the solution to the maximization problem 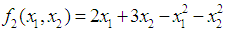 using the Variance Weighted Gradient (VWG) method is
using the Variance Weighted Gradient (VWG) method is 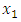
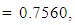
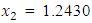 and
and 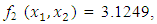 from an initial starting point,
from an initial starting point, 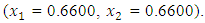 QN, GA, MADS and GPS methods obtained the respective solutions
QN, GA, MADS and GPS methods obtained the respective solutions 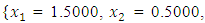
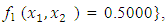
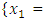
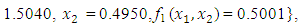
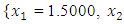
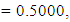
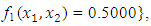
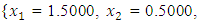
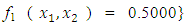 to the minimization problem
to the minimization problem 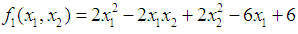 from respective initial guess value,
from respective initial guess value, 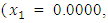
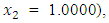
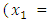
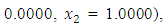
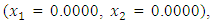
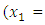
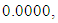
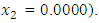 Similarly, QN, GA, MADS and GPS methods obtained the respective solutions
Similarly, QN, GA, MADS and GPS methods obtained the respective solutions 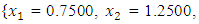
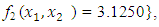
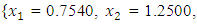
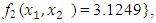
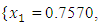
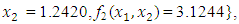
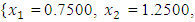
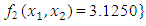 to the maximization problem
to the maximization problem 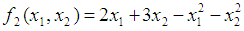 from respective initial guess value,
from respective initial guess value, 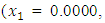
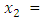
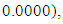
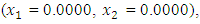
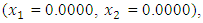
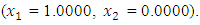 The summary results are as tabulated in Tables 1 and 2.
The summary results are as tabulated in Tables 1 and 2.
|
|
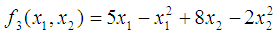 subject to
subject to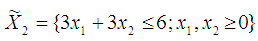 (Hillier and Lieberman, 2001)andMaximize
(Hillier and Lieberman, 2001)andMaximize 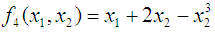 subject to
subject to 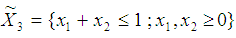 (Hillier and Lieberman, 2001)The solution to the maximization problem
(Hillier and Lieberman, 2001)The solution to the maximization problem 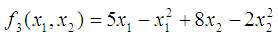 using the Variance Weighted Gradient (VWG) method is
using the Variance Weighted Gradient (VWG) method is 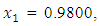
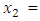
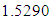 and
and 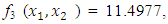 from an initial starting point,
from an initial starting point, 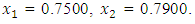 Similarly, the solution to the maximization problem
Similarly, the solution to the maximization problem 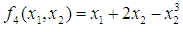 using the Variance Weighted Gradient (VWG) method is
using the Variance Weighted Gradient (VWG) method is 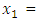
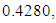
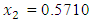 and
and 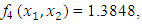 from an initial starting point,
from an initial starting point, 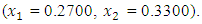 QN, GA, MADS and GPS methods obtained the respective solutions
QN, GA, MADS and GPS methods obtained the respective solutions 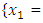
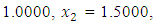
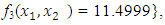
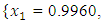
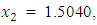
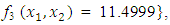
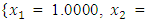
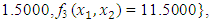
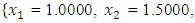
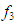
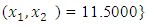 from respective initial guess value,
from respective initial guess value, 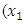
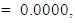

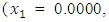
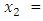
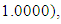
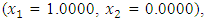
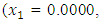
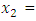
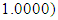 to the maximization problem
to the maximization problem 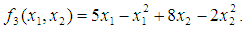 In like manner, QN, GA, MADS and GPS methods obtained the respective solutions for
In like manner, QN, GA, MADS and GPS methods obtained the respective solutions for 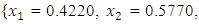
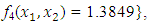
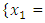
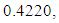
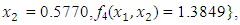
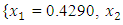
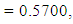
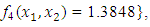
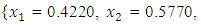
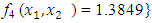 from respective initial guess value,
from respective initial guess value, 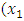
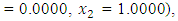
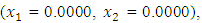
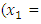
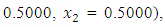
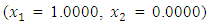 to the maximization problem
to the maximization problem 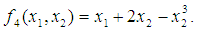 The summary results are as tabulated in Tables 3 and 4.
The summary results are as tabulated in Tables 3 and 4.
|
|
4. Discussion of Results
- In minimizing
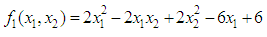 subject to
subject to 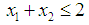 and
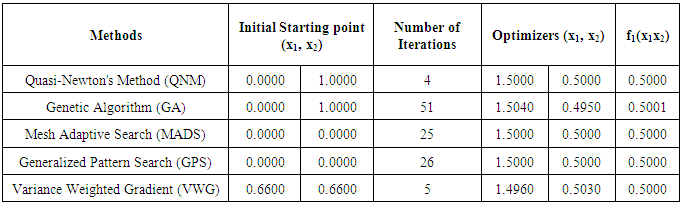
and 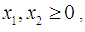 the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (1.5000, 0.5000) in 4 iterations with a response function value of 0.5000. Genetic Algorithm (GA) with initial guess starting points (0.0000, 1.0000) locates the optimizer (1.5040, 0.4950) in 51 iterations with a response function value of 0.5001. The Mesh Adaptive Search (MADS) and Generalized Pattern Search (GPS) methods, with initial guess starting point (0.0000, 0.0000), locate the same optimizer (1.5000, 0.5000) with a response function value of 0.5000 in 25 and 26 iterations, respectively. The Variance Weighted Gradient Method (VWG) obtained optimizers (1.4960, 0.5030) in 5 iterations, with a response function value of 0.5000 from an initial optimum starting point (0.66, 0.66).In maximizing
the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (1.5000, 0.5000) in 4 iterations with a response function value of 0.5000. Genetic Algorithm (GA) with initial guess starting points (0.0000, 1.0000) locates the optimizer (1.5040, 0.4950) in 51 iterations with a response function value of 0.5001. The Mesh Adaptive Search (MADS) and Generalized Pattern Search (GPS) methods, with initial guess starting point (0.0000, 0.0000), locate the same optimizer (1.5000, 0.5000) with a response function value of 0.5000 in 25 and 26 iterations, respectively. The Variance Weighted Gradient Method (VWG) obtained optimizers (1.4960, 0.5030) in 5 iterations, with a response function value of 0.5000 from an initial optimum starting point (0.66, 0.66).In maximizing 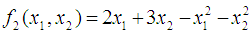 subject to
subject to 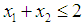 and
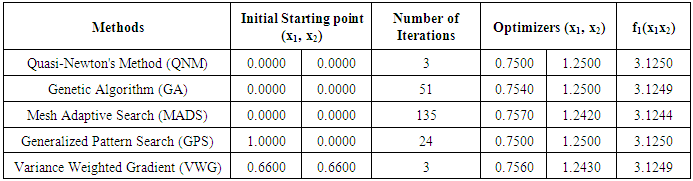
and 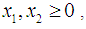 the Quasi-Newton Method (QNM) method, with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7500, 1.2500) in 3 iterations with a response function value of 3.1250. The Genetic Algorithm (GA), with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7540, 1.2500) in 51 iterations with a response function value of 3.1249. The Mesh Adaptive Search (MADS) method, with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7570, 1.2420) in 135 iterations with a response function value of 3.1244. The Generalized Pattern Search (GPS) method, with the initial guess starting point (1.0000, 0.0000) locates the optimizer (0.7500, 1.2500) in 24 iterations with a response function value of 3.1250. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.7560, 1.2430) in 3 iterations, with a response function value of 3.1249 from an initial optimum starting point (0.66, 0.66). In maximizing
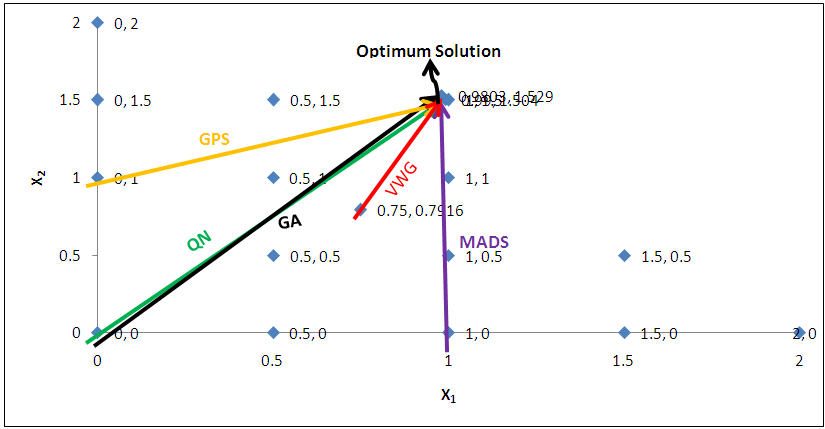
the Quasi-Newton Method (QNM) method, with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7500, 1.2500) in 3 iterations with a response function value of 3.1250. The Genetic Algorithm (GA), with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7540, 1.2500) in 51 iterations with a response function value of 3.1249. The Mesh Adaptive Search (MADS) method, with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.7570, 1.2420) in 135 iterations with a response function value of 3.1244. The Generalized Pattern Search (GPS) method, with the initial guess starting point (1.0000, 0.0000) locates the optimizer (0.7500, 1.2500) in 24 iterations with a response function value of 3.1250. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.7560, 1.2430) in 3 iterations, with a response function value of 3.1249 from an initial optimum starting point (0.66, 0.66). In maximizing 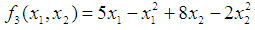 subject to
subject to 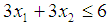 and
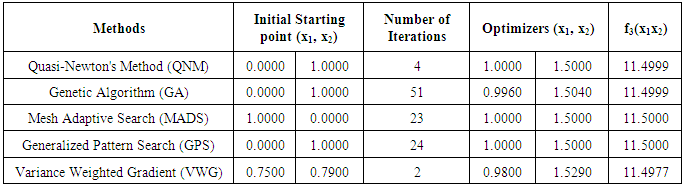
and 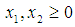 , the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (1.0000, 1.5000) in 4 iterations with a response function value of 11.4999. Genetic Algorithm (GA) with initial guess starting point (0.0000, 1.0000) locates the optimizer (0.9960, 1.5040) in 51 iterations, with response function value 11.4999. The Mesh Adaptive Search (MADS) method with initial guess starting point (1.0000, 0.0000) locates the optimizer (1.0000, 1.5000) in 23 iterations, with response function value 11.5000. The Generalized Pattern Search (GPS) method with initial guess starting point (0.0000, 1.0000) locates the optimizer (1.0000, 1.5000) in 24 iterations, with response function value of 11.5000. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.9800, 1.5290) from an initial optimum starting point (0.7500, 0.7900) in 2 iterations, with response function value of 11.4977.
, the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (1.0000, 1.5000) in 4 iterations with a response function value of 11.4999. Genetic Algorithm (GA) with initial guess starting point (0.0000, 1.0000) locates the optimizer (0.9960, 1.5040) in 51 iterations, with response function value 11.4999. The Mesh Adaptive Search (MADS) method with initial guess starting point (1.0000, 0.0000) locates the optimizer (1.0000, 1.5000) in 23 iterations, with response function value 11.5000. The Generalized Pattern Search (GPS) method with initial guess starting point (0.0000, 1.0000) locates the optimizer (1.0000, 1.5000) in 24 iterations, with response function value of 11.5000. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.9800, 1.5290) from an initial optimum starting point (0.7500, 0.7900) in 2 iterations, with response function value of 11.4977.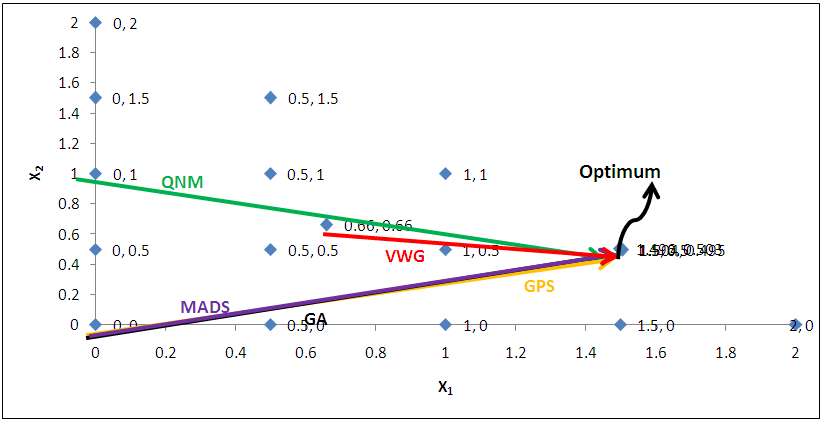 | Figure 1. Optimum Point of 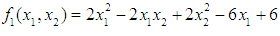 Subject to Subject to 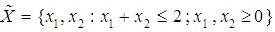 |
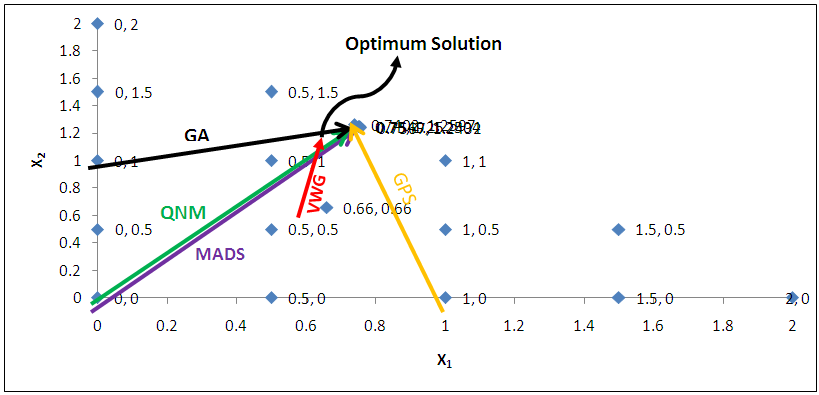 | Figure 2. Optimum Point of 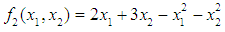 Subject to Subject to 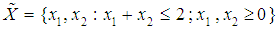 |
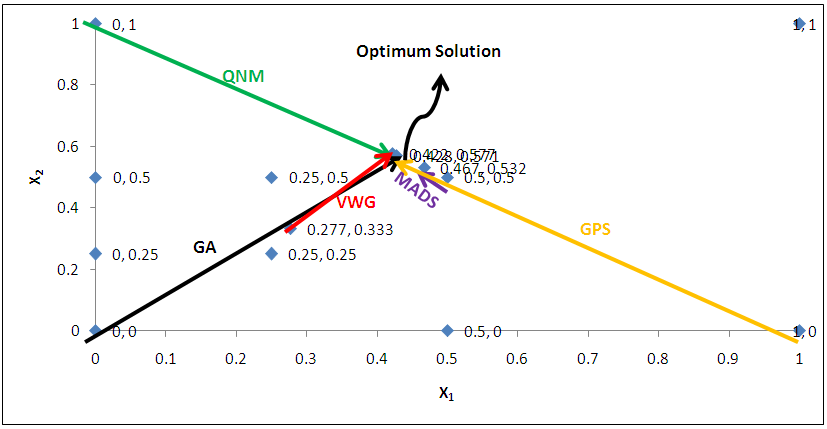
 | Figure 3. Optimum Point of 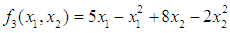 Subject to Subject to 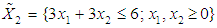 |
 | Figure 4. Optimum Point of 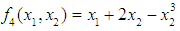 subject to subject to 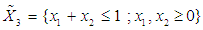 |
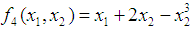 subject to
subject to 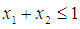 and
and 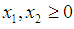 , the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (0.4220, 0.5770) in 5 iterations with a response function value of 1.3849. Genetic Algorithm (GA) with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.4220, 0.5770) in 51 iterations with a response function value of 1.3849. The Mesh Adaptive Search (MADS) method with the initial guess starting point (0.5000, 0.5000) locates the optimizer (0.4290, 0.5770) in 109 iterations with a response function value of 1.3848. The Generalized Pattern Search (GPS) method with the initial guess starting point (1.0000, 0.0000) locates the optimizer (0.4220, 0.5770) in 40 iterations with a response function value of 1.3849. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.4280, 0.5710) with the initial starting point (0.2700, 0.3300) in 3 iterations with a response function value of 1.3849. The VWG method has the ability to obtain optimizers for polynomial response functions defined on joint and disjoint feasible regions simultaneously in either the first or second iterations. The comparative assessment shows that results obtained using the VWG simultaneous optimization are comparatively efficient in locating the optimizers of several response surfaces. The norm of the optimizers obtained using the VWG methods relative to the existing methods is very small, with the maximum recorded as 0.0352. Also, the absolute difference between the values of the response functions obtained using the new method relative to existing methods are approximately zero. The present study raises the possibility that optimizers of multifunction defined on joint feasible region can be added to the design points of the region and also the optimizers of multifunction defined on one feasible region can be projected to another feasible region in obtaining optimal solutions. We propose that further research should be undertaken to investigate multifunction polynomial response surfaces defined by constraints on different feasible regions and multifunction polynomial response surfaces for unconstraint.
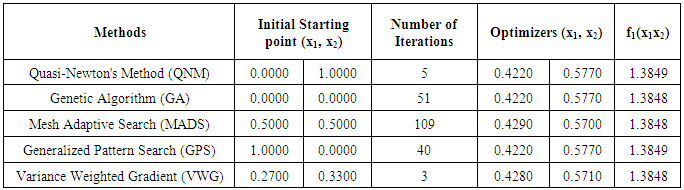
, the Quasi-Newton Method (QNM) with the initial guess starting point (0.0000, 1.0000) locates the optimizer (0.4220, 0.5770) in 5 iterations with a response function value of 1.3849. Genetic Algorithm (GA) with the initial guess starting point (0.0000, 0.0000) locates the optimizer (0.4220, 0.5770) in 51 iterations with a response function value of 1.3849. The Mesh Adaptive Search (MADS) method with the initial guess starting point (0.5000, 0.5000) locates the optimizer (0.4290, 0.5770) in 109 iterations with a response function value of 1.3848. The Generalized Pattern Search (GPS) method with the initial guess starting point (1.0000, 0.0000) locates the optimizer (0.4220, 0.5770) in 40 iterations with a response function value of 1.3849. The Variance Weighted Gradient Method (VWG) obtained optimizers (0.4280, 0.5710) with the initial starting point (0.2700, 0.3300) in 3 iterations with a response function value of 1.3849. The VWG method has the ability to obtain optimizers for polynomial response functions defined on joint and disjoint feasible regions simultaneously in either the first or second iterations. The comparative assessment shows that results obtained using the VWG simultaneous optimization are comparatively efficient in locating the optimizers of several response surfaces. The norm of the optimizers obtained using the VWG methods relative to the existing methods is very small, with the maximum recorded as 0.0352. Also, the absolute difference between the values of the response functions obtained using the new method relative to existing methods are approximately zero. The present study raises the possibility that optimizers of multifunction defined on joint feasible region can be added to the design points of the region and also the optimizers of multifunction defined on one feasible region can be projected to another feasible region in obtaining optimal solutions. We propose that further research should be undertaken to investigate multifunction polynomial response surfaces defined by constraints on different feasible regions and multifunction polynomial response surfaces for unconstraint.5. Conclusions
- The variance weighted gradient (VWG) methods are suitable for optimizing polynomial response surfaces defined on the same or different feasible experimental regions. For both cases, the starting point of search is not a guess point as commonly seen in many gradient and non-gradient algorithms. Although the two variance weighted gradient methods simultaneously optimize multiobjective functions, in handling problems involving different regions and different constraints, a projection scheme that allows the projection of design points from one design region to another is used. The projection scheme enhances fast convergence of the algorithm to the desired optima as measured by the number of iterative moves made. The results of this study establish that the variance weighted gradient methods are reliable optimization methods for optimizing polynomial response surfaces defined by constraints on joint and disjoint feasible regions, when compared with Quasi-Newton’s Method, Genetic Algorithm, Mesh Adaptive Search and Generalized Pattern Search method. Interestingly, VWG algorithms required few numbers of iterative steps in obtaining the optimizers of the polynomial response functions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML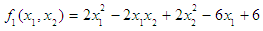 Subject to
Subject to 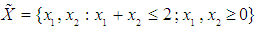
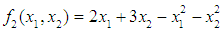 Subject to
Subject to 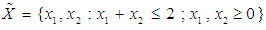
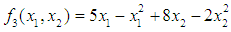 Subject to
Subject to 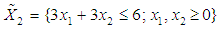
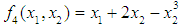 Subject to
Subject to